有限生成群作用的Gromov-Hausdorff跟踪性

刘鑫磊, 董美花

( 延边大学 理学院, 吉林 延吉 133002 )

0 引言

由于伪轨跟踪性对研究拓扑稳定性具有重要作用,且它与轨道的渐近性质密切相关,因此近年来一些学者对其进行了研究[1-6].2017年,Arbieto等[7]首次将同胚上的GH-距离应用于拓扑动力系统中,此后一些学者在此基础上研究了Gromov-Hausdorff意义下的拓扑动力系统.例如:2021年,Dong等[8]将GH-距离从同胚映射推广至有限生成群作用,并在Gromov-Hausdorff意义下研究了群作用的拓扑稳定性;2022年,Lee等[9]在Gromov-Hausdorff意义下研究了同胚的拓扑稳定性和跟踪性.基于上述研究,本文将文献[9]中的同胚映射推广至有限生成群作用,并得到如下结果:若群作用具有伪轨跟踪性,则其具有Gromov-Hausdorff跟踪性(GH-跟踪性);若群作用具有GH-跟踪性,则其具有等距跟踪性.

1 预备知识

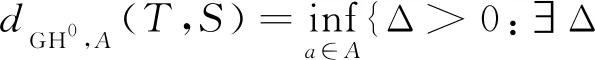
定义1对于任意的ε>0,若存在δ*>0,使得对于任意的0<δ<δ*和满足dGH0,A(T,S)≤δ的任意有限生成群作用S∈Act(G,Y)存在δ-等距映射j:Y→X;且若对于S的任意δ-伪轨{yg}g∈G存在x∈X,使得d(Tg(x),j(yg))≤ε:则称有限生成群作用T∈Act(G,X)关于生成元集A具有GH-跟踪性.

注1当群G为整数加群时,有限生成元集A={1,-1}.由于此时的群作用T是紧致度量空间X上的同胚映射,因此同胚上的GH-跟踪性为定义1的特例.因由文献[4]中的性质1易证定义1不受生成元选取的影响,故本文在此省略.

定义2若有限生成群作用T∈Act(G,X)关于生成元集A具有GH-跟踪性,则称T具有GH-跟踪性.

定义3对于任意的ε>0,存在δ*>0,使得对于任意0<δ<δ*和满足dGH0(T,S)≤δ的有限生成群作用S∈Act(G,Y)存在δ-等距映射j:Y→X;且若对于任意y∈Y,存在x∈X,使得d(Tg(x),j(Sg(y)))≤ε成立:则称群作用T具有弱GH-跟踪性.

注2GH-跟踪性与弱GH-跟踪性二者的不同之处为:前者是S的δ-伪轨,后者是S的真轨.但由于每个S的真轨一定是S的δ-伪轨,所以当T具有GH-跟踪性时,T一定具有弱GH-跟踪性.

定义4对于任意的ε>0,存在δ*>0,使得对于任意的0<δ<δ*存在δ-等距映射j:Y→X;且若对于T的任意δ-伪轨{xg}g∈G,存在x∈X,使得d(Tg(x),j(xg))≤ε对于任意g∈G均成立:则称群作用T具有等距跟踪性.

2 主要结果及其证明

定理1若群作用T具有伪轨跟踪性,则T具有GH-跟踪性.

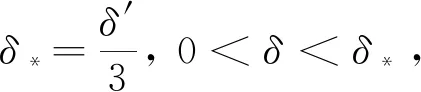
d(Ta(j(yg)),j(yag))≤d(Ta(j(yg)),j(Sa(yg)))+d(j(Sa(yg)),j(yag))≤

δ+δ+d(Sa(yg),yag)≤3δ≤δ′.

由上式可知,{j(yg)}g∈G是T的δ′-伪轨.由于T具有伪轨跟踪性,因此可知存在x∈X,使得d(Tg(x),j(yg))≤ε成立,故T具有GH-跟踪性.定理1证毕.

定理2若T具有GH-跟踪性,则T具有等距跟踪性.

证明给定ε>0,并根据群作用T的GH-跟踪性选取δ*.若0<δ<δ*,则令S=T,由此可得dGH0(T,S)=0<δ.因此存在δ-等距映射j:Y→X,使得对于S的任意δ-伪轨{xg}g∈G存在x∈X,使得d(Tg(x),j(xg))≤ε对于任意的g∈G均成立,故T具有等距跟踪性.定理2证毕.

根据定理1与定理2的证明,可以得到以下几种跟踪性质间的关系:

T具有伪轨跟踪性

T具有GH-跟踪性⟹T具有弱GH-跟踪性

T具有等距跟踪性.