二维耗散非线性薛定谔方程解的时间衰减估计
2024-01-05郭佳鑫李春花
延边大学学报(自然科学版) 2023年4期
郭佳鑫, 李春花
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
本文考虑如下二维耗散非线性薛定谔方程的初值问题:
(1)
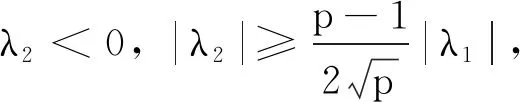
1 预备知识
本文主要利用文献[9]中的求解强耗散非线性薛定谔方程解的时间衰减估计的方法来求解二维耗散非线性薛定谔方程初值问题(1)解的Lq-时间衰减估计.本文在证明过程中主要涉及到以下符号、公式和空间:
1)Fourier变换.定义F:f为定义Fourier逆变换F-1:ff∨为
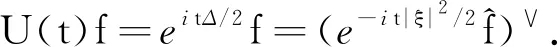
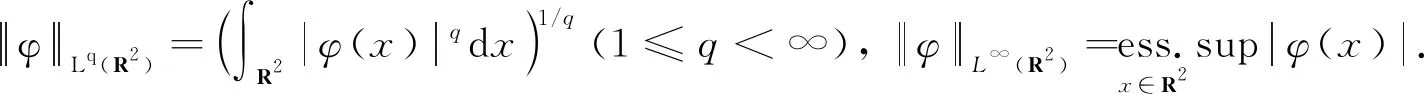
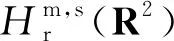
其中S(R2)为速降函数空间.
6)定义R2上的函数空间X1,T(R2)为:
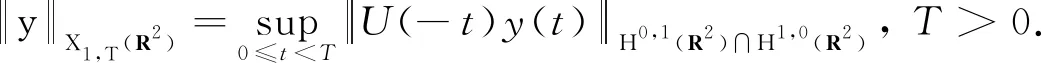
2 主要结果及其证明
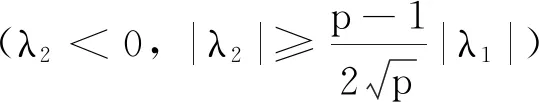
为了证明定理1,本文首先引入如下引理.
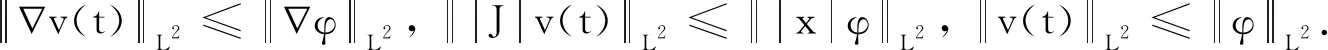
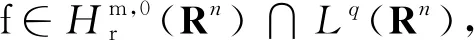
(2)
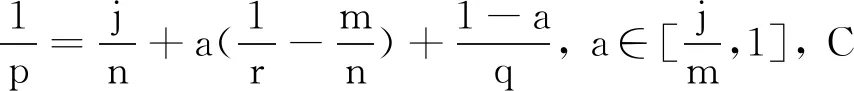
定理1的证明由文献[9]中定理1可知,初值问题(1)存在唯一全局解v∈X1,∞.下面证明解v的时间衰减估计.对式(1)两端作用U(-t)可得:
(3)
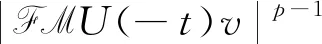
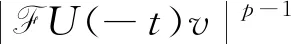
(4)
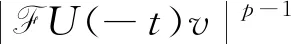
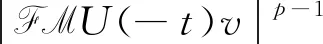
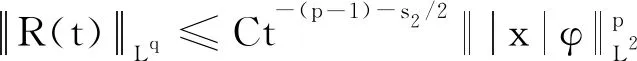
证明对R(t)进行计算后R(t)可表示为:
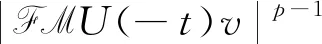
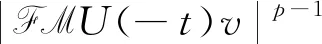
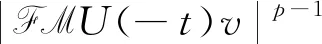
(5)
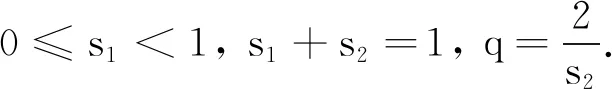
(6)
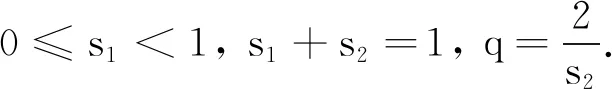
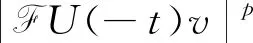
(7)
由于方程(Imλ)-1tp-1H-pdH-dt=0,因此求解此方程可得:
(8)
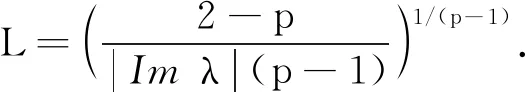
∂t(H-p|FU(-t)v|)≤|Imλ|t-(p-1)(pH-1|FU(-t)v|-(H-1|FU(-t)v|)p)+CH-pR(t).
(9)
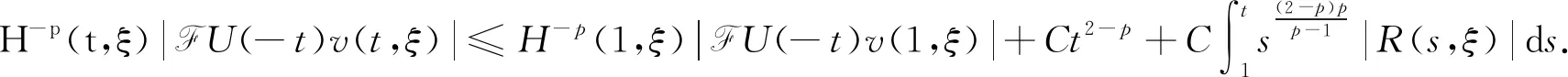

因此可得:
其中0<β<1.对上式取Lq范数并应用引理3可得: