基于有限元分析的高温管道法兰密封设计

李 洋，丁克勤*，王荣仁，舒安庆

1. 武汉工程大学机电工程学院，湖北 武汉 430205；2. 中国特种设备检测研究院，北京 100026

螺栓与法兰密封是一种常见的机械密封方式，其原理是通过螺栓将法兰与密封面紧密连接，从而实现密封。为了提升法兰连接系统的可靠性与密封性，需要对螺栓与法兰的连接进行研究，而为了提升该密封性能，通常是探究各参数对垫片泄露的影响，以及确定垫片系数和垫片比压力，以便为螺栓法兰连接系统的设计提供较为合理有效的参考依据。何川等［1］采用有限元分析法建立了美国机动工程师协会的分体法兰连接油管有限元模型，分析了O 型密封圈的预压缩率、工作油压、油管装配前的径向偏差、角度偏差等对法兰连接密封性的影响规律，研究发现O 型密封圈的密封性与其预压缩率以及工作油压关系密切。张延华［2］研究了垫片在系统温度变化时对螺栓预紧力的影响，进而研究与法兰密封性能的关系。搭建了DN100、PN63 螺栓-法兰平台，并分别研究在常温和100 ℃工况下，螺栓剩余预紧力的变化规律。采用主流的二次加载预紧力来补偿损失的预紧力的方法，实验测得，常温工况和100 ℃工况下螺栓预紧力的平均损失分别为40%与30%左右，由此表明二次热紧能有效的预防螺栓预紧力的损失。栗 伟［3］采 用 系 统 分 析（analysis of systems，ANSYS）有限元分析方法对带法兰椭圆形封头进行建模仿真分析，并与带法兰椭圆形封头进行实验验证对比，同时用ANSYS 软件对其壁厚进行了优化设计，得出结论：壁厚为8.03 mm 时，最大等效应力和最小总质量分别为312.3 MPa 和26.2 kg，相比壁厚为10 mm 时最小总质量下降了16.5%。Adamek 等［4］对2 组不同的聚四氟乙烯填充螺旋缠绕垫片结构进行实验研究，结果和数值分析证明了绕组非对称形状的垫片具有比标准设计时更大的刚度，以及更佳的密封性。与标准垫片相比，非对称垫片在载荷作用下具有更大的有效接触面。

在密封过程中，螺栓的预紧力使得法兰与密封面之间的接触面压紧，从而形成一个密封的界面。同时，由于法兰和密封面的表面粗糙度不同，密封面之间会产生微小的凸起和凹陷，这些凸起和凹陷之间的空隙被填充了密封材料，进一步增强了密封效果。此外，螺栓的预紧力还可以使得密封面之间的接触面保持一定的压力，从而在使用过程中防止松动和泄漏。作用在垫片上以达到密封、防止松动、地漏等目的的最小单位压力称为比压［5］。当与法兰连接的管道达到工作压力时，内压的轴向力使法兰有分离的趋势，而螺栓有伸长的趋势，垫片上的压力会降低。当作用在垫片有效截面上的压力降到某一临界值时，密封仍能保持。此时，垫片上的剩余压力是垫片的有效拧紧力。当垫片上的压力小于其有效拧紧力时，法兰会泄漏甚至吹走垫片，因此垫片的有效拧紧力必须大于管道的工作压力［6］。当2 个法兰密封面之间的距离大于初始工作状态时，垫片和法兰密封面的紧密性由垫片的回弹力保证。可以说，在密封的早期，垫片表面的塑性变形对填充法兰密封面的微观非均匀性起决定性作用；而在法兰密封的运行状态下，垫片内部的弹性恢复起主导作用［7］。

影响密封的主要因素如下：

（1）操作状态下为介质的压力、温度和物理化学性质。石化装置低压法兰较多，压力或介质对法兰泄漏的影响并非主要因素。结合温度考虑时，当谨慎对待。当温度反复变化时，密封失效的可能性较大。

（2）垫片系数m（剩余比压系数）和垫片比压力σy（最小有效压紧应力）对设计参数的影响。以上2 个参数都可参考《钢制压力容器——分析设计标准（2005 年确认）》JB 4732—1995 来选择取值范围，但即使是同一材质下的垫片系数和比压力，也同时与垫片宽度、预紧压力、介质性能、法兰密封面宽度和粗糙度等因素有关。因此，暂无法依据标准来直接确定以上2 个参数的具体值。

本文采用主流的Taylor-Waters 法对该连接系统垫片处进行紧密性分析，利用ANSYS 有限元分析方法建立高温管道法兰连接系统的三维有限元模型，结合JB 4732—1995［8］，对法兰接头进行强度评定，通过对该连接系统的温度场规律分析以及对其法兰连接不连续部位进行沿路径的线性化分析，得出其螺栓、法兰、垫片的应力强度远符合其许用应力范围，表明该垫片具有良好的密封性，且螺栓与法兰的强度均能较好地满足要求。该方法提升了高温管道法兰连接系统的可靠性与密封性，对其设计有一定的参考价值。

1 螺栓载荷的计算

为满足一个常规法兰接头的紧密性，要求垫片所受应力能够在预紧条件下，满足密封整个系统的最小初始压紧应力。在操作工况下，垫片的残余预紧应力应超过所需的最小压紧应力。通常，给出准确的螺栓负载载荷较为困难，尤其是在对垫片性能缺乏全面了解的情况下，传统的方法只能是理论假设、简化计算或根据项目实践经验总结和判断。经过许多科学家多年的研究，现已经有了相关设计的方法，并在有关标准中出现［9］。

Taylor-Waters 法［10］是一种应用于法兰连接分析的方法，可计算螺栓的压紧力。该方法基于弹性力学理论，通过考虑螺栓的预紧力、摩擦系数、螺栓直径和材料弹性模量等因素，对螺栓连接的受力状况进行综合分析，能够估算出螺栓连接中的压紧力。这种方法应用广泛，能够为压力容器领域的设计和分析提供可靠的参考。

根据Taylor-Waters 法的介绍，在不考虑其他外部载荷的情况下，仅通过垫片的参数设计，在预紧和操作条件下，分别计算该状态下垫片所需的压紧力，从而得到法兰连接接头必要的螺栓载荷与面积，进而以螺栓载荷校核该法兰连接系统的强度。已知垫片的系数m和垫片比压力σy，得如下计算方法。

预紧工况下的螺栓载荷计算：

在预紧工况下，螺栓载荷力Fb1等于垫片所受应力σa1，此时可据垫片所需要的垫片比压力得公式（1）：

式中，b为有效密封宽度，DG为垫片压紧力作用中心圆直径。

2 有限元模型设计

由于高温管道法兰连接系统模型有较好的周期对称性，法兰共有8 个螺栓，为了简化计算，由圣维南原理［11］可知，为消除边缘应力影响，法兰接管长度应大于2.5（R1为管道平均半径，d1为管壁厚度）。通过计算，法兰接管长度2.5的计算值为100.62 mm，此次建模法兰接管长度取110 mm，采用1/8 的法兰连接系统模型进行计算。据此，选取管道法兰通径为89 mm，法兰外径为200 mm，厚度为20 mm；螺栓孔直径为18 mm，螺栓型号为M18，数量为8 个；垫片外径为109 mm，厚度为3 mm。垫片为石墨波齿复合垫片，垫片骨架材料和螺栓、螺母材料为304 不锈钢。管道、法兰和螺栓取相同材料，且其弹性模量为200 GPa，泊松比为0.3。在软件SolidWorks 中建立各个部件的三维模型并完成装配。再将模型导入ANSYS Workbench 中进行仿真计算。

对整体模型简化后，模型的计算量较小，故可适当地加密部分网格使计算结果精度更高。在ANSYS Workbench 的Mesh 菜单中进行网格设置，上下法兰、垫片、管道、螺栓和螺母网格大小均为2 mm。

该管道法兰连接系统的接触状态设置如表1［12］所示。

3 载荷及边界条件

热分析过程只考虑法兰持续性工作的稳态阶段［13］（忽略设备加热和停止冷却阶段），对法兰、垫片和螺栓、螺母的导热系数λ进行调整。从理论上讲，法兰内壁的温度不能完全与管道中加热器的温度一致，因此设置内壁的温度为398 ℃。法兰外壁与空气对流传热，垫片外表面、上法兰环下表面和下法兰环上表面的对流传热系数为10 W/(m2·℃)。螺栓中与空气接触部分的对流传热系数为20 W/(m2·℃)，而其外表面其余部分由于与大气直接接触，对流传热系数略高，为32 W/(m2·℃)。上述螺栓与螺母、螺母与法兰面直接接触良好，彼此传热效果好，热阻较小。对于整个研究模型，没有特殊配置的表面均被认为是绝热的［14］。

在热结构耦合分析之前，要设置用于分析法兰模型结构的边界条件和负载。对于这种法兰模型，在上法兰的端部施加轴向约束，仅限制其轴向偏移，并对法兰模型的周期性对称面施加对称约束。同时预紧螺栓，据式（1）螺栓载荷力的计算，得螺栓预紧力为50.24 kN，取整为51 kN，并将该预紧力应用于螺栓上，该状态称为预紧工况；通过分析预紧力条件，可以锁定先前添加的预紧力，对法兰内壁面施加1 MPa 内压，并施加法兰自由端内压产生的等效应力，这种状态称为承压工况［15］。自由端等效膜应力σz为：

式中p为内压，R2为圆筒半径，d2为圆筒厚度。

经式（2）计算可知σz= 2.125 MPa。在承压工况计算完成后，将热分析过程中所得对流换热参数的结果作为温度负载加之于法兰模型中，以模拟实际运行条件。

4 温度场分析

分别作沿上法兰径向（路径1）、上法兰环外侧沿周向（路径2）的路径化温度场分析，结果表明：上法兰的温度值沿半径方向近似的呈线性下降趋势，如图1（a）所示。图1（b）表示为沿路径2 方向（法兰环外侧沿周向）的温度分布，体现为两边大中间小，表明中间部位散热较快，是因为螺栓与法兰的良好接触将法兰中间部位的热量散失了。

图2 为双头螺栓柱沿轴向（路径1）的温度分布图，可知螺栓柱上下两侧温度相对于中间平面对称分布，近法兰内侧温度高于外侧，最高温度190.41 ℃，最低温度158.31 ℃。最高温度出现在螺栓与法兰直接接触的位置，该位置热阻小，传热效果好。最低温度出现在螺栓的两端，这是因为与空气接触时快速冷却导致的。

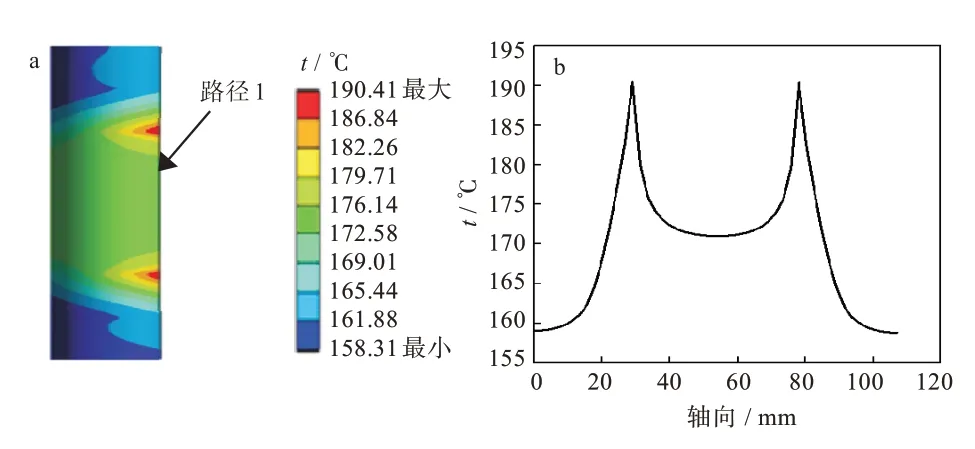
图2 双头螺栓柱的温度分布（a）及螺栓柱沿路径1 的温度分布（b）Fig.2 Temperature distribution of stud column（a）and stud column along path 1（b）

图2（b）为螺栓柱沿路径1 由上而下的温度分布，可知上螺母至上法兰与螺栓柱接触的部位温度逐渐升高，上下法兰与螺柱接触的位置至螺柱中间段裸露在空气中的位置，温度逐渐下降，由下法兰与螺柱接触的位置至下螺母温度又逐渐升高，经分析，这是由于螺柱中间裸露在空气中的部分与空气对流传热，温度下降较快。

图3 为螺母的温度分布图，且据图5 可知，上下螺母温度场呈对称分布；上螺母出现的最大温度（由于管径转换所致）为226.96 ℃，故图3 中展示为上螺母的温度分布。螺母距垫片最近的位置温度高，距离垫片最远的温度较低，因为螺母距垫片最近位置相对于上法兰接触应力最大，传热效果好，故而温度高；距垫片最远的位置不仅是传热距离远，而且是直接与空气对流传热，因此温度较低。

图3 上螺母的温度分布Fig.3 Temperature distribution diagram of nuts

分别作垫片沿径向（路径1）以及周向（路径2）的路径化温度分析，其沿路径1和路径2的温度分布如图4 所示，总体来看垫片温度由内至外逐渐降低。其沿路径1 温度逐渐减小，沿路径2 近似不变，温差仅为4 ℃。

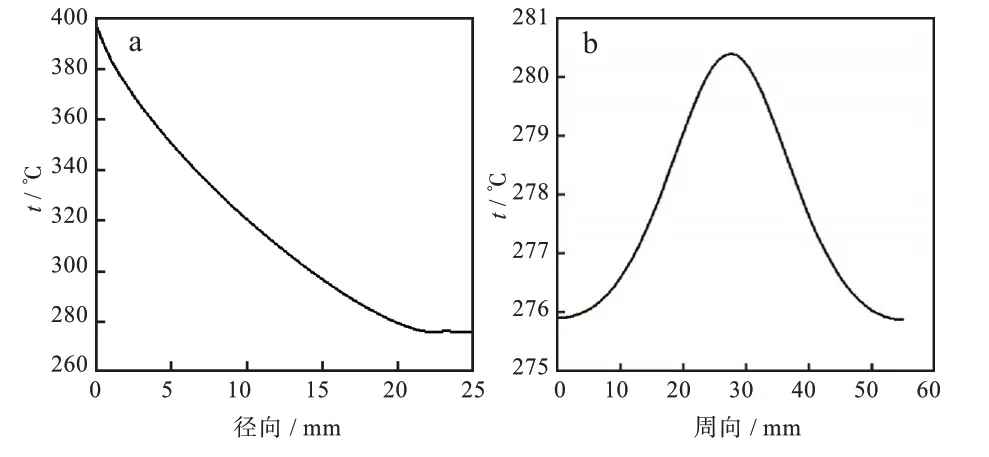
图4 垫片沿路径的温度分布：（a）路径1，（b）路径2Fig.4 Temperature distribution of gasket along paths：（a）path 1，（b）path 2

螺栓法兰连接系统的温度场分析结果表明：上下法兰、上下螺母呈现明显对称趋势，法兰内外壁温度沿半径方向逐渐降低，沿轴线方向呈先增后减趋势。最高温度出现在法兰的内表面，最低温度出现在上下螺母的外表面。

5 试验台高温管道法兰紧密性分析

5.1 法兰强度评定

在上文所述载荷及边界条件下，法兰连接系统处于不同工况时的应力分布云图如图5 所示。当螺栓预紧力51 kN 时，预紧工况下的最大等效应力σ′为265.95 MPa，承压工况下的最大等效应力为288.99 MPa，操作工况下的最大等效应力为338.33 MPa；处于预紧工况时的最大等效应力比承压工况小23.04 MPa，承压工况时比操作工况小49.34 MPa。基于该载荷及边界条件下，处于不同工况时的上下法兰，在应力分布特征上具有明显的对称性。

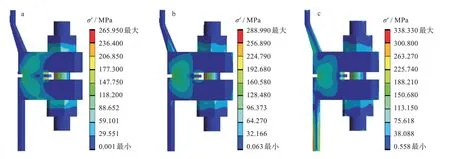
图5 不同工况下法兰连接系统的应力分布云图：（a）预紧，（b）承压，（c）操作Fig.5 Stress distribution cloud maps of flange connection system under different working conditions：（a）pre-tightening，（b）pressure bearing，（c）operating

对于任何不同结构的模型，在其结构的不连续位置处，应力相对较大［16］，即危险截面或危险点，故只需对上法兰进行研究。在上法兰危险截面处，确定4 条路径，如图6 所示，据JB 4732—1995的规定，对法兰强度进行评定，在操作状态下产生的薄膜应力为一次局部薄膜应力σL应小于1.5Sm（Sm为基本许用应力强度），一次应力加二次应力σL+σb+σq应小于3Sm（σb为一次弯曲应力，σq为二次应力）。4 次不同预紧力下法兰的应力评定见表2。将表中的局部薄膜应力与总应力的数据与相应的评判标准进行比较，可知法兰在51 kN 预紧力作用下的强度，能够满足材料的许用应力要求。

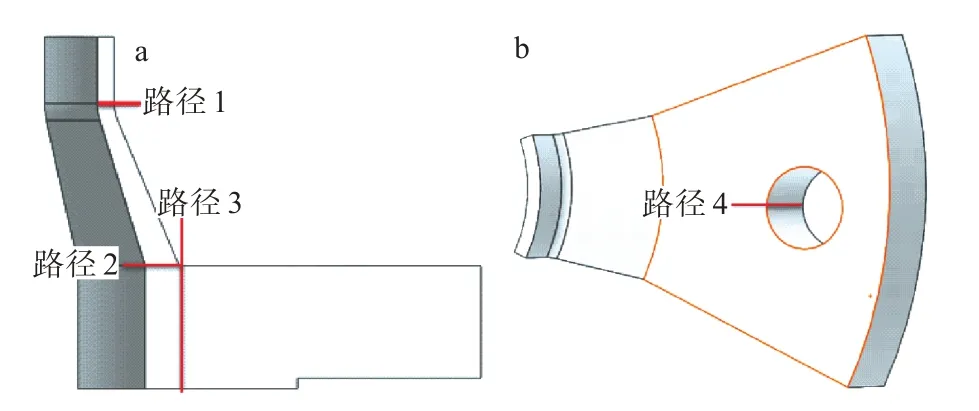
图6 法兰应力强度评定路径图：（a）路径1-3，（b）路径4Fig.6 Path diagrams for intensity assessment of flange stress：（a）path 1-3，（b）path 4

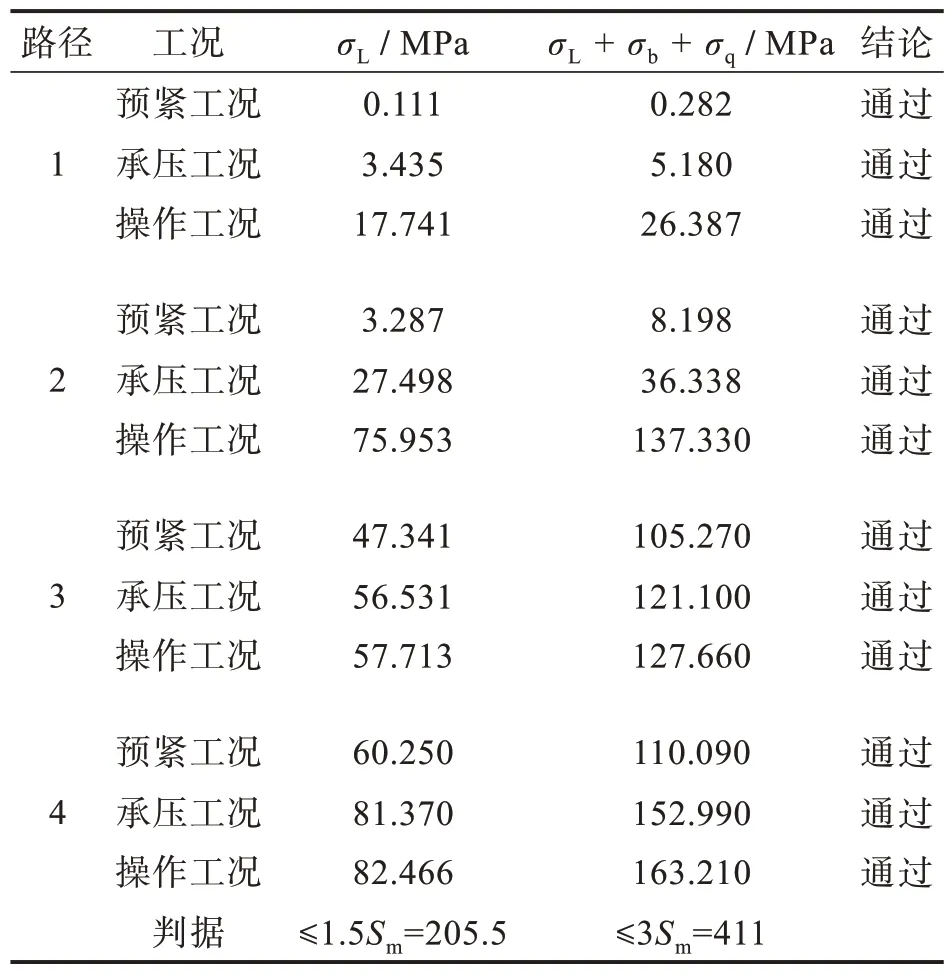
表2 法兰强度评定Tab.2 Evaluation of flange strength

5.2 螺栓强度评定

据上文对法兰连接系统施加的载荷及边界条件，可知预紧工况、承压工况和操作工况下螺栓、螺母应力云图如图7 所示。

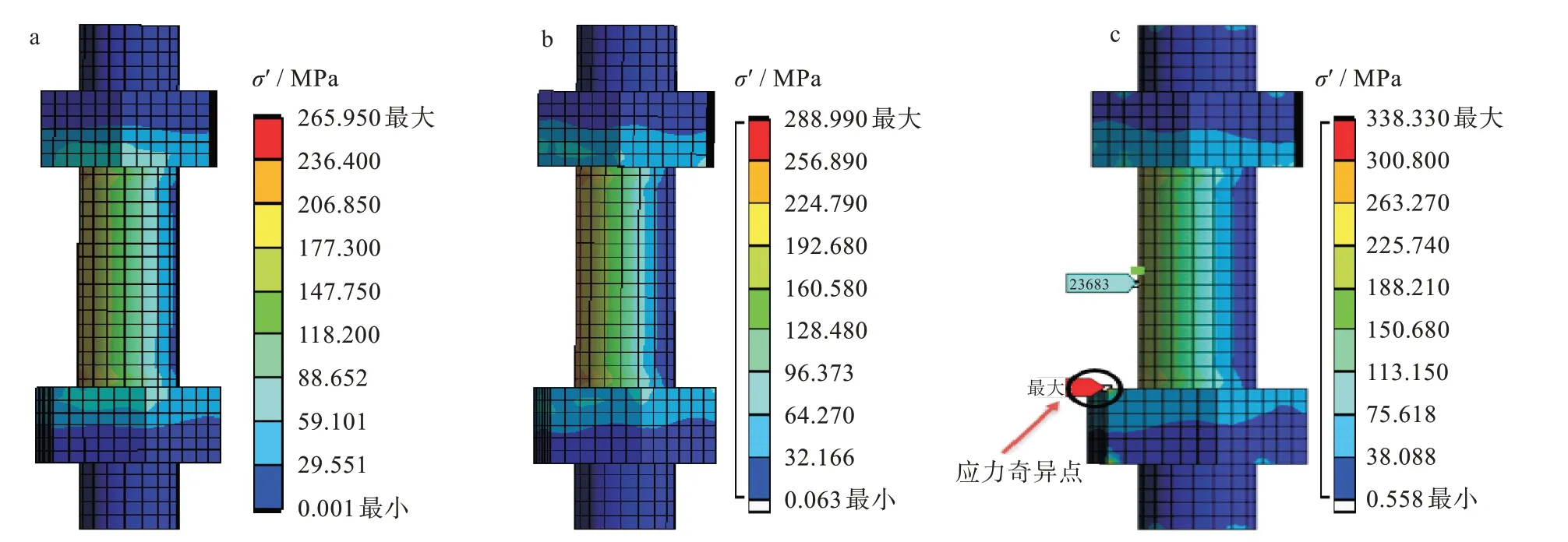
图7 不同工况下螺栓、螺母应力分布云图：（a）预紧，（b）承压，（c）操作Fig.7 Cloud maps of stress distribution of bolts and nuts under different working conditions：（a）pre-tightening，（b）pressure bearing，（c）operating

由图7 可知，在螺母上存在应力奇异现象［17］，螺栓所受应力关于中截面上下对称分布；螺栓及螺母的最大应力位于两螺母与螺栓连接处内侧面，且为与螺栓中面最近的部位，近内侧螺栓沿轴向应力分布为先增后减再增，故螺栓内侧承受沿轴向的压应力。相反螺栓外侧承受沿轴向的拉应力，因此外侧螺栓的应力值较小。螺栓与螺母连接时，沿螺母下边沿作径向路径化分析，用于评定螺栓强度，该路径会经过螺栓与螺母连接的第1 个螺纹根部应力最大处。螺栓评定结果见表3，可以看出在该路径下的强度校核满足要求。

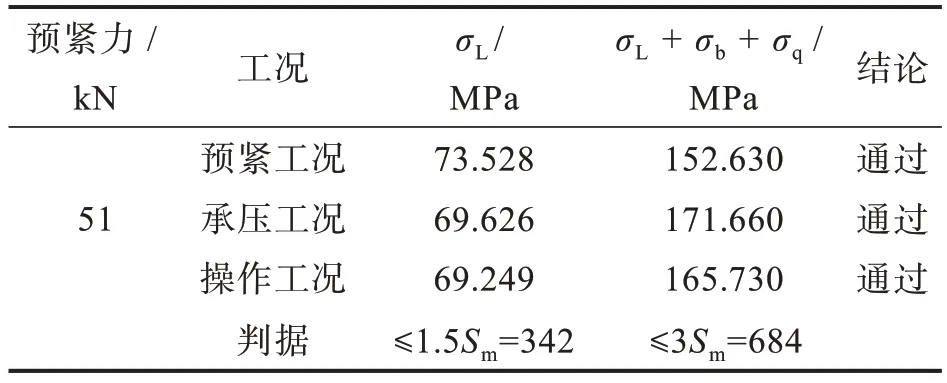
表3 螺栓强度评定Tab.3 Evaluation of bolt strength

5.3 垫片密封评定

图8（a）中表明在螺母上存在应力奇异现象。垫片在螺栓预紧力作用下，越靠近螺栓受到的螺栓预紧力（压应力）作用越明显，故在法兰管道与垫片接触的最外侧位置存在最大等效应力。垫片在预紧工况、承压工况和操作工况下的压应力分布云图如图8 所示。

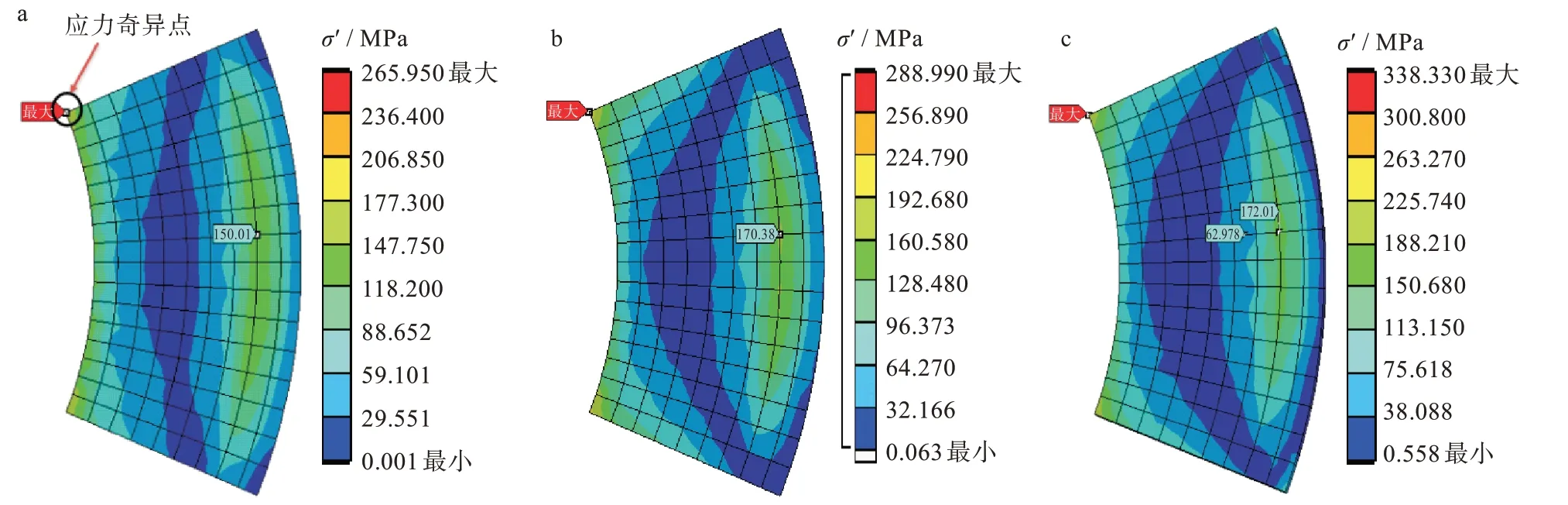
图8 不同工况下垫片压应力分布云图：（a）预紧，（b）承压，（c）操作Fig.8 Cloud maps of shim pressure stress distribution under different working conditions：（a）pre-tightening，（b）pressure bearing，（c）operating

法兰连接系统的密封性主要是由垫片决定，各种工况下垫片的应力分布的变化范围和应力分布的特征是保证其密封的关键，图8 表明垫片压应力云图的分布趋势相同，给垫片做径向（半径方向）路径分析。预紧工况和承压工况下垫片的接触应力要大于垫片的初始密封比压，本次仿真垫片为柔性石墨金属波齿复合垫片，由《压力容器第3 部分：设计》GB/T 150.3—2011 查得该复合垫片的垫片系数m=3，垫片比压力σy=50 MPa，垫片密封性评定见表4，评定结果显示各工况下垫片密封性均良好。

表4 垫片密封评定Tab.4 Evaluation of gasket sealing

6 结 论

为保证试验台高温管道处的法兰连接系统的安全性与可靠性，本文提出了一种法兰密封设计的方法。利用ANSYS 有限元分析方法，建立高温管道法兰连接系统的三维有限元模型。对法兰连接系统的稳态温度场分布进行了详细的分析，得到了该法兰连接系统在高温条件下的温度变化规律。对该连接系统各部件的法兰连接不连续部位进行沿路径的线性化分析的结果表明：法兰内外壁温度沿半径方向逐渐降低，沿轴线方向呈先增后减趋势，法兰环外侧沿周向温度沿中面基本呈对称分布。螺栓上下两侧温度相对于中间平面对称分布，内侧高于外侧，最高温度在螺栓与法兰直接接触的位置，最低温度出现在螺栓的两端。其次，对该连接系统各部件进行强度分析，据JB 4732—1995，得各工况下的垫片压应力均远大于其初始密封比压，表明该垫片具有良好的密封性，且螺栓与法兰的强度均能较好的满足要求。本文的研究对高温高压工业设备密封泄漏领域问题的处理以及高温管道法兰连接系统的设计具有一定的参考价值和借鉴意义。