基于方波注入的无滤波器PMSM初始位置检测*

王淑旺,王 强,杨 光

(合肥工业大学机械工程学院,合肥 230009)

0 引言

内部永磁同步电机(interior permanent magnet synchronous motor,IPMSM)已广泛运用于新能源汽车、工业机器人、数控机床等领域。通常,转子位置信息由位置传感器(如旋转变压器和编码器)获得。然而,传统的机械位置传感器安装维护成本高,并且外部噪声和额外的电缆会降低信号的可靠性。为了克服这些缺点,无位置传感器控制技术逐渐成为研究热点。在中等或高速范围内,当反电动势(electromotive force,EMF)足够大时,通常采用基于模型的方法。基于IPMSM的数学模型以及定子电压和电流来估计转子位置。然而,在低速运行区域甚至静止时,反电动势不够大,不可能使用基于模型的方法准确估计位置。因此,基于转子凸极效应的高频电压注入法已被广泛接受[1-3]。

李文真等[4]采用将周期的离散电流信号转换成连续信号之和进行处理,辨识磁极极性但是并未提出所取信号的幅值和宽度不当,会导致定子电流过大;并且采用了低通滤波器,会滞后高频信号的相位。李抑非等[5]提出了一种六组等宽电压脉冲注入法,该方法向电机定子绕组按特定的顺序注入三相逆变电路的6个非零电压矢量,通过电流响应判断磁极方向,但是该方法得不到准确的转子位置。

传统的高频信号注入方法在对高频正弦信号处理中,都会采用滤波器,滤去高频信号,得到包含位置信息的直流信号。但是滤波环节不仅会滞后信号的相位,还会对幅值造成影响,最终影响辨识的精度[6]。因此国内外很多学者提出了无滤波器转子初始位置辨识[7-9]。YOON等[7]最早提出了高频方波注入情况下,利用转子的凸极性来追踪低速情况下转子的位置,但是却没有研究零速情况下转子极性如何辨识。张国强等[10]利用两次相邻响应电流采样值进行运算分离载波信号的方法,利用矢量叉乘方法解耦位置误差信息,通过龙贝格位置观测器获取转子位置辨识值,最后通过累计一定数量d轴高频响应电流幅值的方法判断转子极性,但是并未就数据点的取法做出解释,并且在高频注入的情况下,d轴高频响应电流存在很多噪声,对极性判断会造成很大的干扰。王淑旺等[11]分析了龙贝格观测器和三阶扩张状态观测器(extended state observer,ESO)在低速状况下永磁同步电机无位置传感器控制系统的带宽和动态响应性能,验证了ESO相较于龙贝格观测器拥有更好的观测性能和鲁棒性但是没有对磁极极性进行辨识。

基于以上研究,本文提出了一种更易实现的高频方波注入无滤波器PMSM转子初始位置辨识方法。首先在观测的d轴注入逆变器开关频率一半的高频方波信号,通过无滤波器载波信号分离,提取出不含基波信号的高频响应电流,采用矢量叉乘解耦位置误差信息,通过位置观测器获取磁极位置,最后根据电机的凸极饱和效应,通过正反脉冲注入法,分析d轴的响应电流波形,来判断转子磁极极性,实现PMSM任意位置启动。

1 基于高频方波注入的转子位置检测

1.1 永磁同步电机数学模型

因为基波运行频率远小于方波信号注入频率,所以可以忽略定子电阻压降和反电动势影响,PMSM在高频信号激励下可等效为感性负载,PMSM的数学模型可表示为:

(1)

式中:udh和uqh,idh和iqh分别为d、q轴高频电压分量和高频电流分量,下标h表示高频,dt是对时间的微分。

1.2 无滤波器高频方波注入法磁极位置辨识

图1 无滤波器高频方波注入PMSM转子位置辨识原理图

(2)

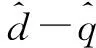
(3)

把定子电流从静止的α-β轴系转换到d-q轴系可以得到:

(4)

将式(3)、式(4)带入到式(1)可得α-β轴系下的高频响应电流,化简可得:

(5)

式中:Lavg是平均电感,Ldif是差值电感,相应的表达式分别为Lavg=(Ld+Lq)/2,Ldif=(Ld-Lq)/2。

由式(5)可知,当Ld≠Lq时,iαh、iβh中就包含了转子位置信息。

当观测器收敛时,θerr≈0,式(5)可化简为:

(6)

由(6)式进一步可得:

(7)

虽然理论上可以通过反正切函数直接获得观测角度值,但是高频注入下直接提取出来的iαh、iβh信噪比很低,所以该方法鲁棒性很差。因此,本文先采用无滤波器载波信号分离,再用矢量叉乘的方法提取出位置误差信号,最后通过观测器获得转子位置。

任一时刻的高频响应电流可表示为:

(8)

式中:iα,βh(n)、iα,β(n)、iα,βf(n)表示n采样时刻高频响应电流矢量、采样电流矢量和基波电流矢量。由式(8)可得n采样时刻高频响应电流矢量和基波电流矢量表达式:

(9)

传统的载波信号分离需要用到低通滤波器或陷波滤波器,载波信号提取则需要用到带通滤波器。但是滤波器的使用,特别是高阶滤波器的使用,必定会降低系统的动态性能,占用更多的系统资源。无滤波器载波分离原理图如图2所示。该方法采用简单的代数运算就可以提取出高频响应电流矢量和基波电流矢量。

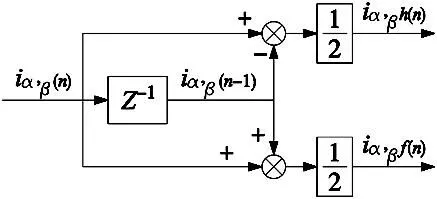
图2 无滤波器载波分离原理图

由式(7)可知分离出的高频响应电流包含了转子的位置信息,但是也包含了很多噪声信号,因此需要对误差信息进行解耦,其原理框图如图3所示。最后采用PI等位置观测器便能得到转子位置。

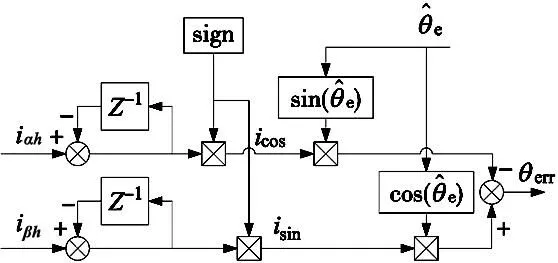
图3 位置误差信号解耦

2 转子磁极极性辨识

虽然无滤波器高频方波注入可以实现在低速段对转子位置信息的辨识,但是当高频方波注入在负向观测转子d轴,观测器依然收敛,此时得到的转子位置观测值显然是错误的。所以需要设计磁极辨识模块配合位置观测器才能实现PMSM的任意位置启动。

PMSM在设计时一般工作在膝点,根据电机的凸极饱和效应,如图4所示,当d轴正向电流增大时,铁芯逐渐饱和,定子电感减小,相同电流引起的磁通变化量减小。

图4 d轴磁链与电流关系图

本文将初始位置辨识分为两步,第一步注入高频方波实现转子位置的初辨识;第二步是在观测的d轴注入幅值相同的正反脉冲,通过比较脉冲注入结束时刻的峰值电流来判断转子d轴位置。

3 仿真与实验验证

3.1 仿真结果与分析

为了验证本文提出的无滤波器高频方波注入转子初始位置辨识策略的可行性,先基于MATLAB/Simulink搭建系统仿真分析模型,模型的原理结构框图如图5所示,仿真采用的PMSM参数与实际参数一致,如表1所示。PWM开关频率为10 kHz,方波注入幅值为20 V,频率为5 kHz,正反脉冲幅值为5 V。

表1 永磁同步电机参数

图5 无滤波器高频方波注入转子初始位置辨识原理框图

转子初始位置分别0.523 6 rad和3.665 2 rad时的初始位置辨识仿真结果如图6和图7所示。

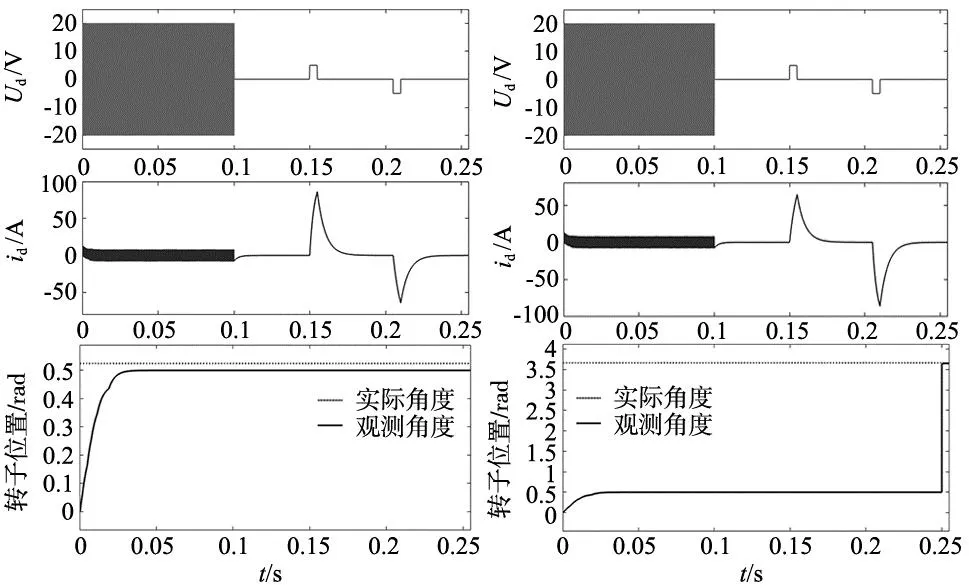
图6 初始角度为0.523 6rad时的位置检测 图7 初始角度为3.665 2rad时的位置检测

由图6可以看出,初始角度为0.523 6 rad时观测器的初始角度在高频方波注入时就逐渐收敛到约0.5 rad,在0.15 s和0.22 s时分别注入正反脉冲,脉冲作用时长0.02 s。两段脉冲之间间隔0.05 s时为了保证上一段电压脉动引起的d轴电流脉动回归于零。此过程中d轴正向峰值电流大于负向峰值电流,因此不需要对辨识角度进行修正。由图7可以看出,初始角度为3.665 2 rad时观测器的初始角度先收敛到约0.5 rad,正反脉冲注入后,d轴正向峰值电流小于负向峰值电流,因此在初辨识位置上修正了π rad。整个初始位置辨识过程约0.25 s。

为了进一步验证模型的正确性,在0～2π rad的范围内均匀地取36个点,记录仿真结果,并绘制成初始位置结果统计图,如图8所示。由仿真结果可知,该初始位置辨识方法的最大误差约为3.6°。

(a) 初始位置检测结果 (b) 初始位置检测误差图8 初始位置检测结果统计

3.2 实验结果与分析

为了进一步验证方法的可行性,本文基于TMS570LS1115芯片实现控制算法,采用科威尔D1000系列高精度双向直流电源供电,通过可变磁阻式旋转变压器测量出转子的实际转速与位置,用于和观测位置进行比较。其他相关参数与表1所列参数相同。实验器平台如图9所示。

图9 实验平台

图10和图11分别为转子在任意位置不带负载与带10 N·m负载启动至100 r/min的实验结果图。

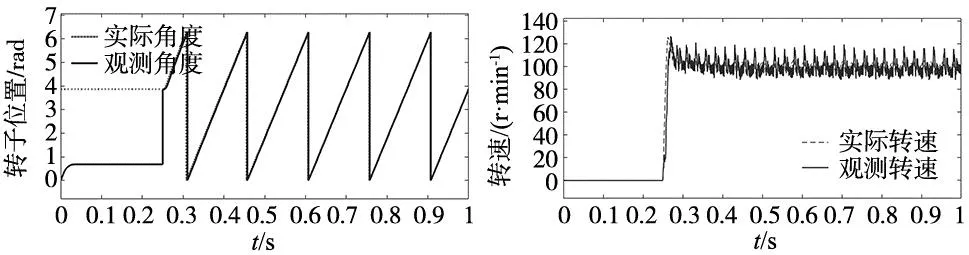
(a) 实际与观测角度 (b) 实际与观测转速图10 0负载启动实验图

图10中转子初始位置为3.864 rad,高频方波注入下转子位置初辨识的结果为0.686 rad,经过极性辨识后在0.25 s时补偿了π rad,最终的转子位置辨识误差约为2.8°。之后不加负载,可平稳启动至100 r/min。图11带载启动实验中,转子初始位置为2.360 rad,高频方波注入下转子位置初辨识的结果为5.523 rad,经过极性辨识后在0.25 s时补偿了π rad,最终的转子位置辨识误差约为1.2°。在0.25 s时给电机施加10 N·m的负载,任能平稳启动至100 r/min。经过大量启动实验初始位置辨识的最大误都在3.6°以内,与仿真结论基本吻合,充分验证了该控制算法鲁棒性强,在PMSM初始位置辨识中有很高的可行性与可靠性。

4 结束语

本文研究了无滤波器基于高频方波注入的PMSM初始位置检测方式,用简单的算法代替滤波器分离出了高频响应电流和基波电流,对高频响应电流运用矢量叉乘法获得了转子位置误差,用PI观测器获得转子位置和速度。最后通过在高频方波中插入一段正反脉冲,通过比较d轴高频响应电流峰值的大小,判断转子极性。该检测方法收敛速度快,可在0.25 s内完成转子初始位置的辨识且辨识误差不到3.6°,实现了PMSM任意位置带载启动。