基于自适应RRT与积分滑模的机器人避障跟踪控制*

张鹏鑫,于海生,李 哲,孟祥祥

(青岛大学 a.自动化学院;b.山东省工业控制技术重点实验室,青岛 266071)

0 引言

针对存在障碍物的场景,机器人如何进行避障[1-3]是一个关键问题,国内外研究人员对其进行研究并提出一些规划算法,比如快速扩展随机树(RRT)算法[4],Dijkstra算法[5],PRM算法[6]以及蚁群算法[7]等。LIU等[8]提出一种时间最优的快速探索随机树算法,满足无碰撞的同时提高了规划速度。JIANG等[9]将RRT算法与人工势场法相结合,利用环境和节点信息使得机器人在短时间内扩展到目标区域,并在实验平台上证明了方法的有效性。李哲等[10]提出一种扩展点选择策略,并优化了随机树的分支,提高了计算效率。

针对目标定位问题,国内外研究人员提出一些视觉伺服[11-13]技术并成功应用于机器人控制。使用最为广泛的视觉伺服算法分为基于位置的视觉伺服(PBVS)[14]和基于图像的视觉伺服(IBVS)[15]。CHEN等[16]在传统的PBVS的基础上引入模糊PID控制,随着位置误差变化,自适应调整PID参数,提高系统的快速性。KRISHNAN等[17]将神经网络与IBVS结合,经过训练的网络根据给定的图像特征调整机器人的姿态,实现精确抓取。LI等[18]提出一种基于PD-滑模控制器的IBVS控制器,通过仿真与实验验证了相比于传统IBVS器控制具有更好的定位精度。

结合以上分析,本文设计了一种便于算法快速收敛的自适应步长和自适应随机概率策略,并使用五次多项式插值对采集到的无碰撞路径点拟合出一条连续光滑的路径减少机器人运行过程中的抖动。在视觉伺服中,设计了一种基于积分滑模的视觉伺服控制器,使得机器人能够快速且精准地跟踪上移动中的目标。在进行理论推导后,对六自由度机器人进行仿真与实验分析,并与已有算法进行比较,进一步验证了所提算法的有效性与优越性。

1 问题描述

1.1 传统RRT算法原理

传统RRT算法的思想是以树的形式快速地在空间中生长出大量分支,寻找出一条可以到达的终点的路径。其基本步骤是:

步骤1:创建树Tree,并初始化起点qstart、终点qend和步长Step;

步骤2:在空间中随机找一点qrand;

步骤3:寻找树上与qrand最近的点qnear;

步骤4:按照指定步长生成新点qnew;

步骤5:判断新点是否可行,可行添加至树中,否则放弃此点;

步骤6:若找到终点,跳出程序,否则返回至步骤2继续寻找路径;

以上每一步对应的示意图如图1所示。

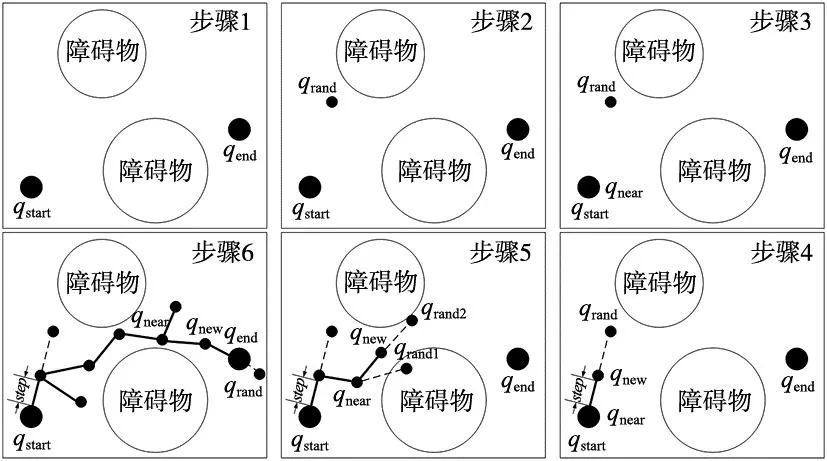
图1 传统RRT算法示意图

虽然RRT算法已经被应用在机器人路径规划领域,但是该算法容易陷入局部最小值且导向性差。本文针对以上缺陷在传统RRT算法的基础上进行相应的改进。

1.2 机器人视觉伺服模型

IBVS的反馈信号是图像特征,没有经过繁琐的位姿估计,影响控制精度的是特征提取的精度。其实现原理如图2所示。

图2 传统IBVS控制原理

用图像雅可比矩阵描述机器人的手眼映射关系,具体公式为:

(1)

为了反映摄像机的运动速度与机器人关节速度的关系,建立机器人雅可比矩阵,其公式为:

(2)

(3)

虽然传统IBVS具有计算效率高,无需经过位姿估计,但是对外部扰动和环境变化较为敏感。本文针对该缺点设计了基于积分滑模的视觉伺服控制器。

2 自适应RRT与视觉伺服控制器设计

2.1 自适应RRT设计

为了避免繁琐的机器人逆运动学求解,本算法在机器人的关节空间下进行设计。

2.1.1 自适应采样概率策略

根据传统RRT算法的步骤2,qrand由人为规定的概率随机产生,但是每次生成的qrand并没有考虑环境因素,随机性强,这无疑增加了计算成本。在本节中,考虑每次生成的qnew是否导致机器人本体与障碍物发生碰撞,来自动调整生成qrand的概率。设计概率计算公式为:

(4)

式中:P为采样概率,noCol为无碰撞标志,s为当前无碰撞次数,i为当前迭代次数。

该算法所计算出的随机采样概率与无碰撞次数具有非常重要的关系,如果无碰撞的次数越多,代表机器人距离障碍物越远,那么采样概率P越大,可以让机器人无条件地向着终点方向生长路径点,达到快速收敛的目的。

2.1.2 自适应步长策略

根据传统RRT算法的步骤4,由于定步长的影响,较长的步长容易碰撞到障碍物,较短步长使得搜索路径的时间增加,不具备随着环境调整的能力。本节根据以上缺点提出自适应步长策略。

首先人为定义初始步长step,然后以该步长进行扩展新点:

(5)

然后根据机器人正运动学,得到机器人末端位置fq,并计算出与每个障碍物表面的距离:

(6)

式中:disj为机器人末端与第j个障碍物的距离,fj为障碍物的中心点,rj为障碍物的半径。

为了方便计算,将dis进行归一化处理:

(7)

式中:dj为距离归一化后的结果。取dj中的最小值,代入式(8),得出自适应步长结果:

(8)

根据以上设计的策略,得出自适应RRT算法流程如图3所示。

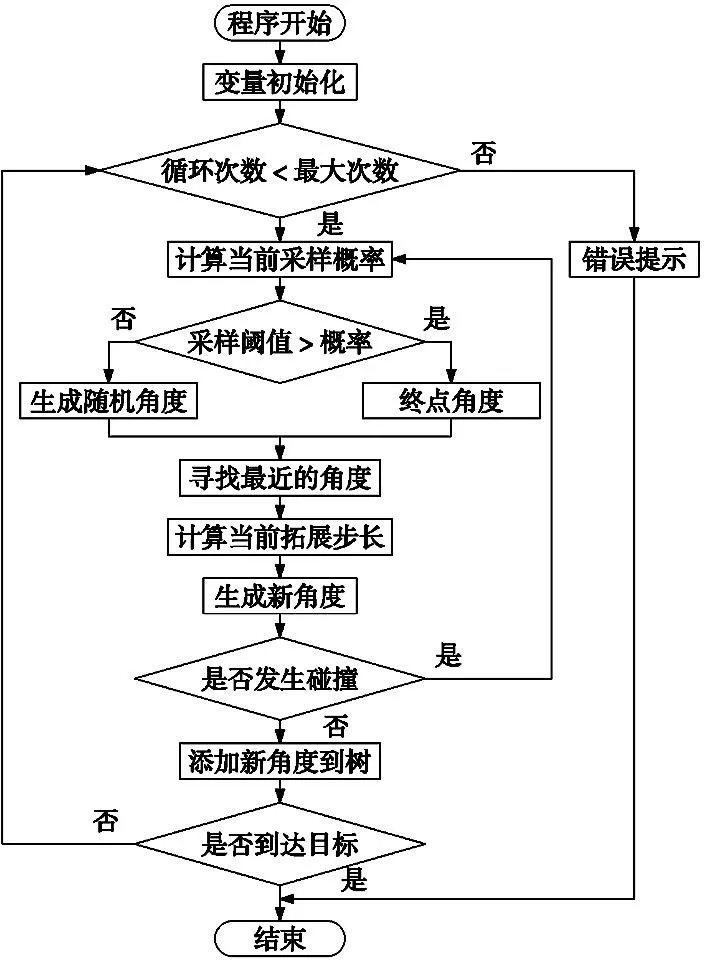
图3 自适应RRT算法流程图

2.1.3 轨迹优化

由于RRT算法得到的是一系列离散的关节角度,这就使得机器人在运行过程中抖动剧烈,不利于机器人平稳运行。为此,采用五次多项式插值算法,将离散的点拟合成平滑曲线,减少机器人在运行过程中的抖动。

q(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(9)

2.2 基于积分滑模的视觉伺服控制器设计

当机器人运行至工作空间时,需要对目标进行跟踪并抓取,控制框图如图4所示。

图4 基于积分滑模的视觉伺服控制框图

2.2.1 公式推导

图像特征点的速度与图像误差有关,因此可以得出传统的视觉伺服控制器为:

(10)

(11)

式中:e=s*-s,s*=[u*,v*]。考虑式(11)的控制器对参数摄动敏感,本节提出了一种基于积分滑模的视觉伺服控制器。定义滑模面:

(12)

(13)

(14)

设a=0.1,δ=0.1,σ∈[-5,5],符号函数与非线性函数对比如图5所示。

图5 符号函数与非线性函数对比

从图中可以看出,当|σ|>δ时,非线性函数的绝对值更大,因此改进的趋近律速度更快;当|σ|≤δ时,非线性函数的波动明显更小更平滑,相比符号函数具有更小的抖振。

对式(12)求导得:

(15)

联立式(11)和式(15)得出控制律:

u=kJ+[-kpe-kσfal(σ,a,δ)-keσ]

(16)

式中:k,kp,kσ,ke≥0。

2.2.2 稳定性证明

设计 Lyapunov 函数为:

(17)

对式(17)求导,将式(13)代入:

(18)

3 仿真与实验分析

3.1 路径规划仿真

在本节的仿真中,利用机器人工具箱导入ABB IRB120机器人模型,其DH坐标系如表1所示。分别在三维坐标(0.18,-0.35,0.1)、(0.22,-0.25,0.355)、(0.28,0.05,0.15)、(-0.22,-0.2,0.21)建立4个直径为0.07 m的球形障碍物,并设置机器人起始关节角度为(-96.1°,-2.6°,23.2°,0°,69.2°,0°),终点关节角度为(45.3°,10.6°,0.8°,0°,78.8°,0°)。

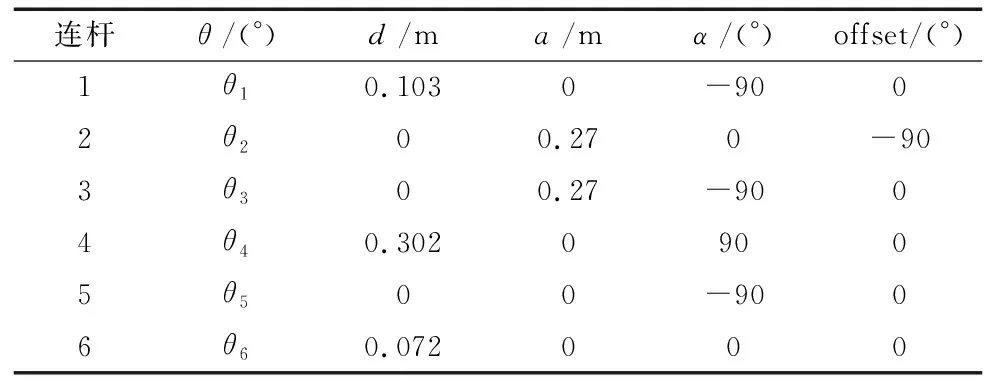
表1 IRB120 DH参数

将传统RRT算法、文献[10]中的RRT算法以及本文提出的自适应RRT算法对比,说明该算法的优越性。3种算法对应的搜索节点和机器人路径如图6～图8所示。

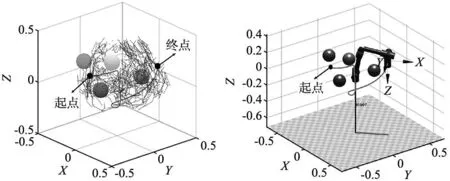
(a) 路径搜索节点 (b) 机器人运动路径图6 传统RRT算法

根据3种算法的对比结果可以看出,本文提出的算法相比另外两种算法具有明显的运动路径短,搜索节点少等优点,使得机器人能够快速地从起点运动至终点。表2的数据展示了3种算法分别进行20次实验各项指标的平均结果。

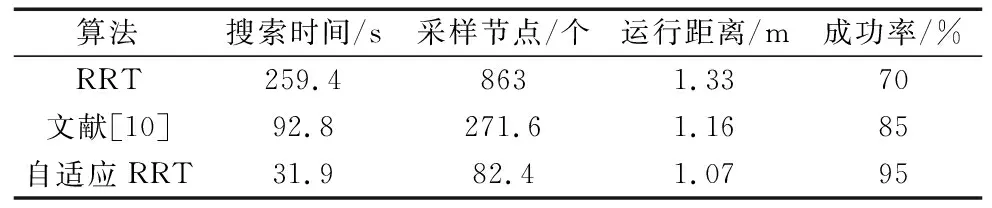
表2 3种算法对比结果

由以上数据可知,自适应RRT算法在路径规划上效果更好。将计算出的路径点用五次多项式插值算法进行平滑处理,得出运行过程的关节角度如图9所示。

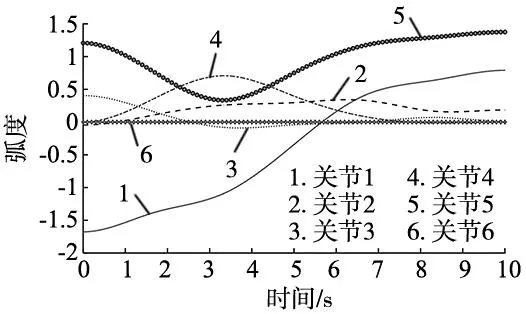
图9 关节角度

3.2 视觉伺服仿真

在本节的仿真中,采用MATLAB视觉伺服工具箱中默认的相机模型,参数如表3所示。

表3 相机模型参数

分别在空间坐标系(0.303,0.305,0.05)、(0.203,0.205,0.05)、(0.203,0.205,0.05)、(0.303,0.305,0.05)设置4个特征点。设计积分滑模控制器参数为kp=2,kσ=0.1,ke=0.001,δ=0.15,a=0.18。为了说明本文提出的视觉伺服的可靠性,将其与传统视觉伺服进行对比,如图10和图11所示。

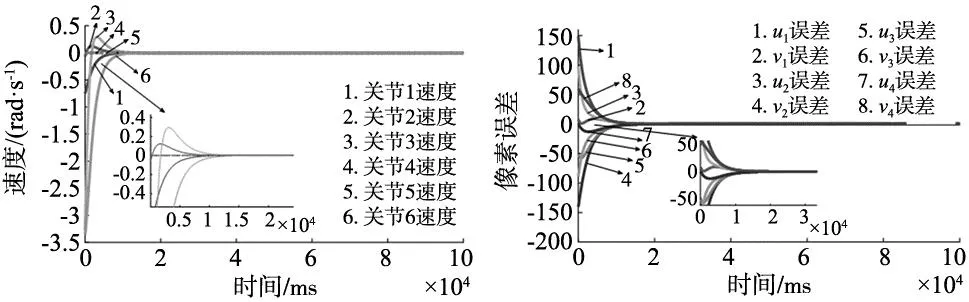
(a) 关节速度 (b) 特征点误差图10 传统视觉伺服

通过对两种控制器的比较,本文所设计的视觉伺服控制器具有更好的快速性,并且在伺服过程中波动更小,机器人能够更加平稳运行。

3.3 实验平台验证

为了进一步验证以上提出算法的可行性,在维视IRVS200开发平台上进行验证。工作站如图12所示。主要硬件由工控机、IRB120机器人、工业相机以及传送带组成。

图12 IRVS机器人工作站

整个实验分为以下步骤:机器人首先从初始状态通过轨迹规划运动至传送带上方,当到达指定位置时,上位机接收到信号,进入视觉伺服过程;然后相机不断地读取图像信息并发送给工控机,由工控机进行图像特征提取,同时将控制信号发送给机器人控制器,直到机器人抓取到目标,一个实验流程结束。在本实验中使用的工业相机型号为MV-EM120M,其参数如表4所示。

表4 MV-EM120M参数

在图像坐标系设置的4个期望特征点分别为(170,385)、(200,70)、(565,110)、(530,425)。调用OPENCV图像处理库,用矩形将目标包围,将提取的4个角点坐标与期望的特征点坐标进行比较,利用本文设计的视觉伺服控制器,对机器人姿态进行校正,直到特征点精度达标。为了说明所设计的视觉伺服控制器的具有良好的跟踪性能,在3种传送带速度下分别进行20次实验,得出的跟踪误差及伺服过程如图13和图14所示。

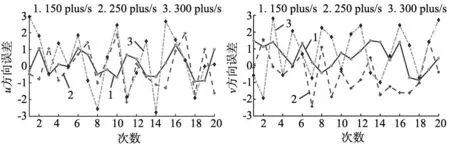
(a) u方向跟踪误差 (b) v方向跟踪误差图13 跟踪误差

图14 视觉伺服过程

以上结果表明,机器人成功通过路径规划运动至工作空间,尽管传送带的速度发生变化,特征点的像素误差始终稳定在可以接受的范围内,使得机器人能够准确跟踪目标,最终实现工件抓取与搬运。

4 结论

本文针对传统RRT算法中采样节点冗余、搜索路径时间长等缺陷,提出一种自适应RRT算法。其中,自适应采样概率策略可以根据无碰撞次数自动调整生成新点的概率,从而减少计算成本;自适应步长策略可以根据工作的环境自动调整扩展新点的步长,从而提高机器人的路径搜索效率。实验结果表明自适应RRT算法具有搜索时间短、节点数少等优势。针对传统视觉伺服在伺服过程具有较大波动、速度较慢等缺陷,提出一种基于积分滑模的视觉伺服控制器。滑模控制具有响应速度快、鲁棒性强等优势,并在滑模面中引入积分项,用于消除系统跟踪过程中的稳态误差。实验结果表明该控制器能够精确跟踪上不同运动速度的目标。以上结果证实了本文提出的算法可以被应用于机器人控制,但是本实验是在已知障碍物的情况下进行的,所以未来的方向将重点考虑如何躲避空间中未知障碍物。