求解PFSP的集成多策略教学优化算法*
2024-01-03亓祥波马志强王宏伟
亓祥波,马志强,王宏伟
(沈阳大学机械工程学院,沈阳 110044)
0 引言
近年来,置换流水车间调度问题(permutation flow-shop scheduling problem,PFSP)因其在运输、采购和通信等行业中占据重要地位而引起了研究人员的关注。由于PFSP是NP难题,求解难度巨大。因此,文献中提出多种改进算法来解决此问题。JOHNSON[1]提出流水车间调度问题,随后NAWAZ等[2]提出NEH启发式算法有效解决了该问题。LIU等[3]在NEH算法基础上,首次利用偏度构造出一个新的优先级规则和新的平局打破机制以进一步提高其性能。由于NEH算法取得了成功,对于求解PFSP的元启发式算法通常采用NEH算法初始化种群来提高解的质量。秦旋等[4]提出混合共生生物搜索算法来改善其局部搜索能力。裴小兵等[5]提出一种基于分布估计算法的改进猫群算法,大幅提高了解的精度。黎阳等[6]提出的改进模拟退火算法为大规模PFSP的求解提供了新思路。ABDEL等[7-9]将鲸鱼优化算法与局部搜索策略相结合来提高算法的求解精度并加快收敛速度,使用最大排序值(largest ranked value,LRV)规则[10]将连续值转换为离散值来求解PFSP。此外,还研究了广义正态分布算法和改进遗传算法,采用加扰变异等算子提高算法性能。
目前智能优化算法得到了广泛的研究,各种改进方法在求解PFSP问题上取得了不错的效果,但仍然存在一些缺陷,例如:易陷入局部最优、鲁棒性较差和时间复杂度较高等问题[11]。尤其在解决中大规模问题时,算法的性能随着问题维度的增加而显著降低,出现维数灾难[12]。为了克服上述问题,本文提出一种集成多策略教学优化算法(IMTLBO),在保留标准教学优化算法优点的基础上,使用多种策略进行寻优,实现算法探索和开发两阶段的平衡。结果表明IMTLBO在求解不同规模PFSP问题上可以得到较优结果。
1 置换流水车间调度问题模型
假设n个工件在流水线中的m台机器上按照一定的顺序加工,给出n个工件的加工排列顺序使得最大完工时间最小。PFSP的环境的布局如图1所示,PFSP的特点总结为:

图1 PFSP的环境布局
在每台机器上,每个工件jb|b=1…n只能被加工一次;在处理时间为PT的机器iz|z=1…m上每次只能加工一个工件;每个工件jb在机器iz上都有一个完成时间C(jb,iz);PFSP建模如下:
C(j1,i1)=PTj1,i1
(1)
C(jb,i1)=C(jb-1,i1)+PTjb,i1forb=2,…,n
(2)
C(j1,iz)=C(jb,iz-1)+PTj1,izforz=2,…,m
(3)
(4)
算法评估每个解决方案的目标函数描述如下:
f(ji→)=C(jb,iz)
(5)
式中:ji→是第i个解的工件排序,并且完工时间最小的排序被认为是最好的。
2 基本教学优化算法
受教师对课堂学习者教学的启发,RAO等[13]提出教学优化算法(TLBO)。TLBO分为教学和学习阶段,教学阶段引导种群逐渐向最优个体收敛,学习阶段赋予种群一定的勘测能力,避免算法早熟。
2.1 教学阶段
TLBO中的教师是整个群体中知识水平最高的成员,该阶段首先确定群体的均值(M),然后根据式(6)确定教师知识水平与群体平均值之间的差异(D)。根据式(7)更新群体中所有个体的知识水平。
D=rand×(Teacher-TF×M)
(6)
Xnew,i=Xold,i+D
(7)
TF=round[1+rand(0,1)]
(8)
式中:Xold,i是群体中第i个成员的当前知识水平向量,Xnew,i是群体中第i个成员的更新知识水平向量,rand为0~1之间的随机数,Teacher表示适应度最好的知识水平向量,TF为教学因子,通过式(8)随机确定。每次计算后,如果个体的适应度得到改善,则进行个体更新,否则不更新。
2.2 学习阶段
学生通过互动来提高知识,两个个体之间的知识交换按式(9)进行。每次迭代中,从群体中选择两个不同的个体,即Xi和Xj,计算目标函数值(以求解最小化问题为例),比较这两个选定个体的值,如果f(Xnew) (9) 式中:f(Xi)和f(Xj)分别是第i个和第j个成员的知识水平向量的目标函数值。 LRV规则[10]可以有效地将连续值映射为离散的工件排列,图2a给出了无重复值的LRV排序,图2b和图2c给出了一个有重复值的排序及解决方案。因此,在LRV用于转换工件排列之前,需通过插入此解决方案中未找到的其他值来删除重复值。 (a) 正确的工件排序 (b) 错误的工件排序 LIU等[3]首次通过引入偏度构造出新的优先级规则PRSKE,开发出新的打破机制TBLJP1,并应用于NEH启发式算法,PRSKE和TBLJP1相结合后命名为NEHLJP1算法。本文初始种群的20%个体通过NEHLJP1算法产生,NEHLJP1算法步骤为: 步骤1:在新的优先级规则PRSKE中,所有工件jb|b=1…n都按以下非递增总和Cb来排序得到序列δ;Cb按下式计算: Cb=AVGb+STDb+abs(SKEb) (10) (11) (12) (13) 式中:AVGb、STDb、abs(SKEb)分别为n个工件在m台机器上加工时间的平均值、标准偏差和偏度的绝对值。 步骤2:令工件排序π={δ(1)},z=2; 步骤3:插入工件δ(z)到完工时间最小位置,若存在多个位置,则根据TBLJP1机制选取最终插入位置; 步骤4:令z=z+1,继续执行步骤3直到满足终止条件,算法运行结束。 其余个体采用反向学习法生成,具体步骤为: 步骤1:由于工件序列为1…n的序列,因此,设置工件编号的最小值为1,最大值为n,当前工序的工件编号设为Ji,则Ji的反向学习编号为: Jn=1+n-Ji (14) 步骤2:对初始种群按照式(14)进行如图3所示的反向学习操作,生成对立种群; 图3 初始种群反向学习 步骤3:将两部分种群合并,计算合并后所有种群的适应度值并从大到小进行排列,选取前80%Np个体作为最终初始种群。 在此阶段,将学习者根据M分为两组。第一组为顶级学习组(T),由成绩高于M的学习者组成。第二组为弱势学习组(W),由其余学习者组成。T组通过教师教学来提高知识,该过程由式(15)表示。W组中的学习者根据M和教师来提高其知识水平,该过程用式(17)表示。 Xnew,i=Xold,i×W+rand(Teacher-Xold,i) (15) (16) Xnew,i=(Xold,i+(rand-0.5)×1.5×(M-Xold,i))×W+D×W (17) D=rand×(Teacher-TF×M) (18) 式中:W是根据式(16)计算的惯性权重参数,其值从ωmax(0.9)非线性递减到ωmin(0.4)。MaxIt是算法的最大迭代次数,Wj是第j次迭代中的惯性权重。 基本TLBO算法中教学因子是2或1的随机取值,这反映了两种极端情况,即学习者100%或0%的从教师授课中学习。TF值较小时,可在较小步长中进行局部搜索,但会导致全局收敛速度缓慢。TF值越大,表示全局搜索速度越快,但会降低局部搜索能力。因此,对基本TLBO算法的TF进行正弦非线性自适应的改进,既能保证算法局部搜索的精确性,也能平衡局部和全局的搜索速度。 (19) 式中:It为当前迭代次数,TFmax和TFmin分别为TF的最大值(取值为2)及最小值(取值为1)。 在改进教学阶段后采取多点变异的方式进行局部搜索,采用如下两种多点变异方式: (1)三点交换变异算子。此算子通过交换从解中随机选择3个位置搜索比当前最佳解具有更小完工时间的其他解,图4a和图4b分别为使用三点交换变异算子的前后顺序。 (a) 使用三点交换变异算子前的位置顺序 (2)两点逆序变异算子。逆序变异算子是对两个不同随机位置之间的子序列进行逆序排列,图5a和图5b分别为使用两点逆序变异算子的前后顺序。 (a) 使用两点逆序变异算子前的位置顺序 学习阶段是TLBO引导最优解的关键阶段,该阶段可以保证算法精确的进行全局搜索。但是,若成绩均较低或学习水平基本相同的学生交流,相互学习将很难发挥作用。因此,引入双学习策略来提高算法的寻优精度,即在标准TLBO的学习阶段进化产生较优个体后,再次从群体中随机挑选两个体进行交流,该交流采用文献[14]的学生混合变异,从而自适应调配学生间的相互学习,式(20)和式(21)为双学习策略的更新表达式为: (20) (21) (22) (23) 式中:β为-1~1之间的随机数,It为当前迭代次数,θ(t)为高斯变异,G(0,1)表示标准高斯分布,δ(T)表示柯西变异,C(0,1)表示标准柯西分布。 双局部搜索(double local search,DLS)为迭代贪婪算法(iterated greedy,IG)与改进的引用插入方案(improved referenced insertion scheme,IRIS)协同搜索,表1为DLS伪代码。 表1 DLS伪代码 (1)基于IG的局部搜索(IGLS)。破坏和构造过程是IG算法的关键部分。在破坏阶段,从序列π中随机选择k个工件删除,该过程产生两个子序列。第一个序列为πD,由n-k个工件组成。第二个序列为πR,由k个工件组成,πR必须重新插入到πD中才能生成完整的候选序列。构建阶段需要利用改进TLBO算法以贪婪的方式重新插入πR里。 通过大量实验,针对不同规模问题采取不同大小的破坏尺寸来重插入工件,具体改进为: (24) (2)IRIS局部搜索。在IGLS之后,进行IRIS局部搜索以进一步提高解的质量。关于IRIS,采用两种非常有效的插入局部搜索策略。第一步是基于改进的插入方案,此过程为插入工件πi(1…n)到目前序列π的所有可能位置,当找到最佳改善位置时,工件πi插入到该位置。对所有工件重复这些步骤。若有改进,将重新进行局部搜索,直到没有发现更好的解。第二步为RIS局部搜索[15]。在局部搜索之后,借鉴模拟退火算法中解的接收机制决定是否接受新解作为下一次迭代的解。其中,退火温度T的值根据式(25)来确定。 (25) 式中:τp为调整的参数,本文设为0.3。 为了求解PFSP,采用NEHLJP1算法和反向学习法结合的精英初始种群。将VNS操作、自适应教学因子、改进教学阶段、双学习策略和双局部搜索与原始TLBO算法结合,集成多策略教学优化算法(IMTLBO),图6为IMTLBO流程图。 图6 IMTLBO流程图 本文在CARLIER[16]、REEVES[17]和HELLER[18]提出的问题上进行实验,算法编码工具为MATLAB R2018b。运行环境为:Win10,Intel Core i5处理器,4 G内存,主频2.5 GHz。为公平对比其它算法,对于Car和Reeves类问题,本文算法种群数量设为40,迭代次数为200。对于Hel类问题,种群数量设为20,迭代次数为100,与对比算法相比保持一致或更小,每个算例均运行20次。对比指标为最优(BRE)和平均相对误差(ARE),计算公式如下: (26) (27) 式中:Cbest和Cavg分别为运行20次完工时间的最小值和平均值,C*为基准实例的已知最优解。 针对每类问题选取不同算法比较,对比算法包括:基于猫群算法的改进分布估计算法(EDA-CSO)[5]、变参数量子进化算法(VP-QEA)[11]、混合回溯搜索算法(HBSA)[12]、高效的广义正态分布算法(IHGNDO)[8]、混合共生生物搜索算法(HSOS)[4]、高效改进的遗传算法(HIEGA)[9]、混合鲸鱼搜索算法(HWA)[7]。 Car实例[16]均为小规模问题,共有8种类型问题,将IMTLBO与EDA-CSO、VP-QEA和HBSA算法对比。从表2分析得出(粗体表示各算法取得的最佳结果)。对于最优值,所有算法均可在Car类实例取得最优值。而对于平均值,只有IMTLBO的ARE均为0,可以体现提出IMTLBO求解的稳定性。从上述分析来看,IMTLBO在小规模问题上无论是精确性还是稳定性都可以取得积极的成果。 表2 与其他算法针对Car实例的比较 为验证IMTLBO的有效性,在Reeves的21个实例[17]进行实验。将其与VP-QEA、IHGNDO和HSOS进行比较,图7和图8分别给出了IMTLBO及对比算法的BRE和ARE的三维瀑布图。在BRE的比较中,IMTLBO优于所有对比算法。针对该指标的平均值,IMTLBO的计算结果仅为0.21。在ARE的比较中,IMTLBO取得18个最优值,数量上排名第一。针对该指标的平均值,IMTLBO的计算结果为0.54,排名依旧第一。图9为Reeves实例下不同规模的IMTLBO、IMTLBO-NL(无局部搜索)、IMTLBO-NG(无改进相互学习)和原始TLBO的迭代曲线,可以看出多种改进策略的有效性,IMTLBO在Reeves实例下依旧具有优势。 图7 与其他算法针对Reeves实例的BRE瀑布图 图8 与其他算法针对Reeves实例的ARE瀑布图 图9 Rec03、Rec09、Rec17、Rec19、Rec29、Rec33、Rec39和Rec41迭代曲线 此外,通过使用95%置信水平的配对t检验来检验比较算法之间的差异。表3给出了各个对比算法的统计比较,从表中可以得出结论,IMTLBO与所有比较的改进算法在统计学上各不相同,有着明显的统计显著性差异。同时,使用Cohen′s d 值表示效应量大小(差异幅度大小),该值越大说明算法之间差异越大(Cohen′s d 值表示效应量大小时,效应量小、中、大的区分临界点分别是:0.20、0.50和0.80),从表3可以看出Cohen′s d的值均大于0.80,呈现大的差异。通过以上结果分析表明,在比较的算法中,IMTLBO对于Reeves实例具有不错的性能,这使得它可以成为解决PFSP的现有算法的有力替代方案。 表3 Reeves实例上各种算法平均相对误差配对t检验分析结果-效应量指标 在Hel实例[18]中,将IMTLBO与HIEGA和HWA进行比较,表4展示了各性能指标值。对于Hel1实例,3种算法均可以求出新的上界值为515。对于Hel2实例,IMTLBO更新了新的上界为135,相比其它算法,各项指标均达到最优,这表明了IMTLBO在求解Hel实例的有效性。为了进一步验证IMTLBO的性能,将种群增加至40,迭代次数增加至200。在Hel1实例上,IMTLBO再一次更新了上界为514,从以上数据可以得出结论,IMTLBO能够更加高效地求解Hel类问题,改进的多种策略是有效可行的。 表4 Hel1和Hel2实例各算法的比较 某汽车发动机零部件公司的生产车间准备制造100种不同型号的发动机连杆部件,该部件主要有9道加工工序,该连杆部件制造为经典的大规模PFSP,加工数据见文献[6],目标是求解这100种不同型号连杆的加工顺序,使得总完工时间最短,从而提高企业生产效率。未优化前,总完工时间是6284 s,利用IMTLBO优化后,总完工时间为5320 s,大幅缩短了完工时间,新的带有调度排序的甘特图如图10所示。优化后,总的加工时间相比未优化缩短15.34%左右,从生产实例中可以进一步说明IMTLBO对于实际生产的作用,再次提高生产效率,并增强了企业的核心竞争力,进一步说明提出的IMTLBO的有效性。 图10 最优调度甘特图 本文提出了一种求解PFSP的IMTLBO算法,采用精英初始种群并集成多种改进策略来提高算法的寻优精度,提出了一种新的局部搜索DLS,并将其作为混合策略嵌入到TLBO算法中以进一步增大其搜索范围。使用三类典型基准实例和一个大规模的实际工程问题评估了提出算法的性能,仿真结果和算法比较表明了IMTLBO在搜索质量和鲁棒性方面的优势。在未来的研究中,将IMTLBO算法应用于解决动态环境下的其他调度问题,如柔性维护活动、机器故障和紧急作业等。3 求解PFSP的集成多策略教学优化算法
3.1 LRV规则编码

3.2 精英初始化种群

3.3 基于惯性权重的分组教学阶段
3.4 正弦自适应教学因子
3.5 变邻域搜索(VNS)


3.6 双学习策略
3.7 双局部搜索

3.8 集成多策略教学优化算法运行流程
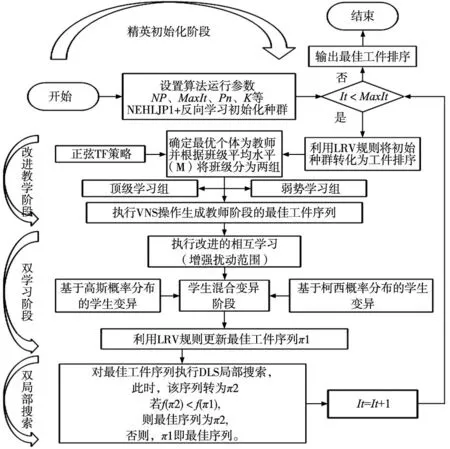
4 实验与分析
4.1 Car类测试集比较

4.2 Reeves类测试集比较



4.3 Hel类测试集比较

5 车间调度优化实例的应用

6 结论
