Stewart并联机构运动Jacobian矩阵表达形式的多样性

尤晶晶,叶鹏达,徐帅,王澍声,黄宁宁,李成刚

(1. 南京林业大学 机械电子工程学院,江苏 南京 210037; 2. 常州大学 机械与轨道交通学院,江苏 常州 213164;3. 南京航空航天大学 机电学院,江苏 南京 210016)

0 引言

与串联机构相比,并联机构具有更紧凑的结构、更高的刚度、更快的响应、更小的累积误差等优势[1],在多维传感器[2-3]等领域应用前景广阔。在所有的6自由度并联机构中,目前应用最广的是Stewart并联机构[4-5]。它主要由1个动平台、1个静平台以及连接2个平台的6条SPS(S为球面副,P为移动副)支链构成。研究发现,Stewart并联机构的很多性能指标,如奇异性、灵活性、各向同性、刚度、可操作度等,都与机构的Jacobian矩阵有关[6]。Jacobian矩阵包括运动Jacobian矩阵和力Jacobian矩阵,它们之间满足对偶性的关系。因此,推导并分析Stewart并联机构的运动Jacobian矩阵有着重要的理论意义和实际价值。

从检索到的文献资料来看,并联机构运动Jacobian矩阵的表达形式五花八门[6-11],且各形式在机构学上的解释以及它们之间的数学关联尚不明确。这影响了机构性能的机理分析和机构拓扑的优化。为解决上述问题,本文从动平台速度的物理定义和数学表达出发,挖掘了Stewart并联机构运动Jacobian矩阵的内涵,推导并梳理了3类Jacobian矩阵的解析表达式,继而剖析了不同形式Jacobian矩阵之间以及它们行列式之间的映射关系。最后,通过数值算例验证了本文结果的正确性,并基于推导出的运动Jacobian矩阵绘制了Stewart并联机构的位置奇异曲面和姿态奇异曲面。

1 转动速度采用不同的表达方式

Stewart并联机构的机构简图如图1所示。

图1 Stewart并联机构的机构简图

分别在静平台和动平台上固连笛卡儿坐标系O-xyz和P-x′y′z′。初始状态下,两坐标系的3个坐标轴分别平行。动平台的自由度为6,包括3维平动和3维转动。其中,3维转动的速度可以用欧拉角及其导数来描述,也可以用角速度矢量来描述。

1.1 欧拉角方式

1)基于欧拉角的旋转矩阵

首先,P-x′y′z′绕z′轴转动进动角Ψ(逆时针方向为正),得到第1次转动之后的坐标系P-x″y″z′。两坐标系之间的旋转矩阵为

(1a)

接着,P-x″y″z′绕x″轴转动章动角θ,得到第2次转动之后的坐标系P-x″y‴z″。它与第1次转动之后坐标系之间的旋转矩阵为

(1b)

最后,P-x″y‴z″绕z″轴转动自转角φ,得到第3次转动之后的坐标系P-x‴y″″z″。它与第2次转动之后坐标系之间的旋转矩阵为

(1c)

执行关于3个绕体轴的子旋转矩阵式(1a)、式(1b)、式(1c)的右乘运算,得到合成的旋转矩阵:

(2)

2)Jacobian矩阵的推导

Stewart并联机构的几何约束方程[12]为

(3)

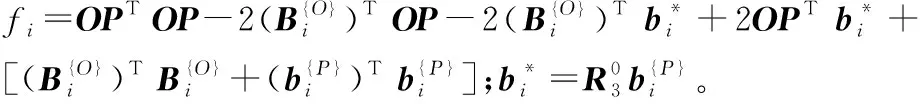
式(3)的等号两边同时对时间求一阶导数,整理后可得线性方程组

(4)

当li≠0,(i=1～6)时,矩阵Jl是可逆的。此时,式(4)可改写为

(5)

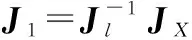
1.2 角速度矢量方式

运用环路方程法[4],列出支链速率的解析式:

(6)

式中:si表示第i条支链的方向矢量[4];ω表示动平台的角速度矢量。

将式(6)整理成矩阵形式:

(7)

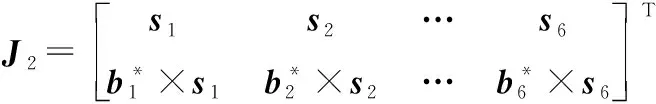
1.3 第1、2类形式Jacobian矩阵之间的映射

根据角速度加法公式,可得坐标系P-x‴y″″z″相对于P-x′y′z′的转动速度:

(8)

(9)

综合式(5)、式(7)和式(9),整理可得第1、2类形式Jacobian矩阵之间的映射关系:

J1=J2T1,2

(10)

也就是说,通过映射矩阵T1,2可以将第1、2类形式的Jacobian矩阵关联起来。

2 平动速度选取不同的基点

理论上,动平台三维平动的速度基点可以任意选择。常用的基点主要有2个:1)动平台的质心(一般也是动坐标系的原点)[4];2)动平台上与静坐标系原点重合的点[13]。第1节在建立平动速度时就是选取的前者,故本节仅讨论后者的情况。

2.1 Jacobian矩阵的推导

将动平台上与静坐标系原点重合的点标记为点O′。同样,运用环路方程法,列出支链速率的解析表达式:

(11)

式中vO′表示O′点的线速度矢量。

将式(11)整理成矩阵形式:

(12)

2.2 第2、3类形式Jacobian矩阵之间的映射

根据速度基点法,可建立O′和P两点速度之间的关系式:

(13)

(14)

综合式(7)、式(12)和式(14),整理可得第2、3类形式Jacobian矩阵之间的映射关系:

J3=J2T3,2

(15)

可见,通过映射矩阵T3,2可以将第2、3类形式的Jacobian矩阵关联起来。

2.3 第1、3类形式Jacobian矩阵之间的映射

综合式(10)、式(15),整理可得第1、3类形式Jacobian矩阵之间的映射关系:

J3=J1T3,1

(16)

式中T3,1=T1,2-1T3,2将第1、3类形式的Jacobian矩阵关联起来。注意:本文不考虑欧拉角奇异点的情况,即默认矩阵T1,2是可逆的。

3 映射矩阵的算例验证

本节对Stewart并联机构在一般位姿下3类形式的运动Jacobian矩阵及其映射矩阵进行算例验证。并联机构尺寸参数的选取如表1所示。

表1 Stewart并联机构的尺寸参数 单位:mm

不失一般性地,随机选择动平台在其工作空间内的一个位姿:OP=(82,158,68)Tmm,Ψ=1.2 rad,θ=2.5 rad,φ=1.7 rad。根据式(3),此时,6条支链的长度(单位:mm)依次为298.541、141.327、181.274、322.265、388.781、277.387。对应的3类形式的Jacobian矩阵以及3个映射运算分别如式(17a)—式(17f)所示。结果显示:1)3个Jacobian矩阵的前3列元素完全相同;2)3个Jacobian矩阵之间的关联和本文的推导结论完全一致。

(17a)

(17b)

(17c)

(17d)

(17e)

(17f)

4 奇异位形

当并联机构的Jacobian矩阵的行列式等于0时,动平台所处的位形称为“奇异位形”[14]。本节研究3类形式Jacobian矩阵的行列式之间的关联。

运用矩阵行列式的乘法定理和分块矩阵的行列式性质,分别处理式(10)、式(15),整理可得:

|J1|=|J2||T1,2|=|J2||A|=-sθ×|J2|

(18)

|J3|=|J2||T3,2|=|J2|

(19)

由于本文不考虑欧拉角奇异点的情况,即sθ不等于0,故由式(18)、式(19)可知:3类形式Jacobian矩阵的行列式等于0的情况是完全等效的。因此,可以通过求解任意一类形式的Jacobian矩阵行列式来判别并联机构是否处于奇异位形。图2(a)、图2(b)分别为作为算例的Stewart并联机构的位置奇异曲面和姿态奇异曲面。在进行机构的轨迹规划时,应避开奇异曲面中的全部坐标点。

图2 Stewart并联机构的奇异曲面

5 结语

1)用欧拉角及其导数描述动平台的转动速度,并选取动坐标系的原点为平动速度基点,可推导出第1类形式的运动Jacobian矩阵。

2)用角速度矢量描述动平台的转动速度,并选取动坐标系的原点为平动速度基点,可推导出第2类形式的运动Jacobian矩阵。

3)用角速度矢量描述动平台的转动速度,并选取动平台上与静坐标系原点重合的点为平动速度基点,可推导出第3类形式的运动Jacobian矩阵。

4)所推导出的3类形式运动Jacobian矩阵的前3列元素完全相同。

5)根据角速度加法公式以及线速度基点法,可建立3类形式运动Jacobian矩阵之间的映射,它们均呈现线性变换的关系。数值算例验证了上述映射矩阵的正确性。

6)根据矩阵行列式的乘法定理和分块矩阵的运算规则,可推导出3类形式Jacobian矩阵行列式之间的关系。在不考虑欧拉角奇异点的前提下,它们所对应的机构奇异位形是完全一致的。

7)上述结论为并联机构的型综合、型优化提供了理论指导。下一步工作是推导3类形式Jacobian矩阵的特征值、奇异值、条件数之间的关系,以建立并完善6自由度并联机构的动力学性能指标。