铜/石墨复合材料热变形行为研究

蒋锦涛，刘 平，陈小红，周洪雷

（上海理工大学 材料与化学学院，上海 200093）

随着轨道交通、电子工业、电力传输设备、航空航天等高科技领域的快速发展，传统铜合金已无法满足要求，迫切需要开发出综合性能更优异的铜合金材料[1]。向铜基体中引入石墨，在保持铜基体良好特性的同时，可以有效地提高复合材料的综合性能，从而获得性能优异的金属基复合材料。

目前，关于铜基复合材料的研究主要集中在制备工艺以及组织性能等方面，而关于该材料热变形行为的研究相对较少。通过热压缩模拟试验，可以研究在不同的变形温度和应变速率下复合材料的热变形行为，进而实现对其热加工工艺参数的优化和组织性能的调控[2]。金属及合金在高温变形下的应力-应变曲线可分为动态回复型和动态再结晶型两种，变形过程包括加工硬化、动态软化和趋于稳态3 个阶段[3]。在热塑性变形的过程中，金属的宏观流动和微观组织演变主要受变形温度、应变速率等宏观条件影响[4]，通过流变应力的变化可表征金属在热加工过程中的塑性变形行为。材料的动态软化和加工硬化受到温度和应变速率的显著影响。堆积断层能量对塑性变形中晶粒和亚晶粒的发育有很大的影响[5]。大多数铜基金属在热变形过程中的动态回复行为主要是由于较低的堆垛层错能[6-8]，较低的堆垛层错能意味着较高的孪晶倾向，在塑性变形过程中会产生更多的孪晶。本研究在不同变形条件下对复合材料试样进行了热压缩实验，分析样品的真应力-真应变曲线，研究变形温度和应变速率与流变应力之间的关系，并计算得到热加工变形的材料常数以及热变形激活能，建立本构方程，绘制材料热加工的耗散图、失稳图，最终得到热加工图。建立材料宏观变形与微观结构演变的内在联系，对实现铜基复合材料热塑性变形过程协同控制具有重要意义。

1 实验

本实验材料为含石墨质量分数1%的石墨增强铜基复合材料，该复合材料使用中频真空熔炼炉制备。

首先对铸态的铜/石墨复合材料进行微观形貌组织分析，通过扫描电子显微镜（scanning electron microscope,SEM）对复合材料的断口截面进行分析，并通过能谱仪（energy disperse spectroscopy，EDS）确定断口截面中的元素成分。使用光学显微镜对铸态复合材料的晶粒组织进行观察。在进行热模拟试验前，利用线切割将铸锭制备成直径为8 mm、厚度为12 mm 的圆柱试样。使用Gleeble-3500 热模拟试验机对圆柱试样进行热压缩试验。试验的变形温度分别为700、750、800、850 ℃，试验的应变速率分别为0.001、0.010、0.100、1.000 s-1。不同变形温度及应变速率两两组合，共计16 组实验数据。热压缩试验的加热速率为5 ℃/s，通过热电偶连接热模拟试验机与试样，以确定试样升温是否正常以及是否达到设定的变形温度。当试样达到设定的变形温度后保温2 min，保温结束后开始热压缩试验。设定试样的压缩变形量为80%，当变形量达到80%后热压缩试验立即停止，并立刻对试样进行水冷，以保留热变形后的组织。利用光学显微镜对复合材料热变形后的组织进行观察，分析其热变形前后微观组织演变规律[9]。

2 结果分析

2.1 铜/石墨复合材料微观组织分析

图1（a）为铜/石墨复合材料断口截面SEM 图。从图1（a）中可以看出，石墨在铜基体中有着较为均匀的分布，石墨颗粒嵌入铜基体中，且与铜基体有着良好的结合，增强相与基体的良好结合有利于复合材料性能的提升。图1（b）为EDS 图。通过图1（b）也可以看到复合材料中含有碳元素，充分证明断口截面中石墨的存在。图1（c）为铜/石墨复合材料的金相组织图。从图1（c）中可以看出，铜/石墨复合材料的晶粒组织较为粗大且不均匀。

图1 铜/石墨复合材料微观组织与成分分析Fig.1 Microstructure and composition analysis of copper/graphite composites

2.2 真应力-真应变曲线

图2 所示为铜/石墨复合材料在不同应变速率下热压缩的真应力-真应变曲线。从图2 中可以看出，变形温度和应变速率对复合材料的流变应力都产生了影响，在应变速率一定时，流变应力随着变形温度的升高而降低；而当变形温度不变时，应变速率越高，流变应力则越大。所有变形条件下的流变应力均在压缩初期随真应变的增加而快速增加。出现这种现象的原因是变形初期，复合材料中位错的数量急剧增加，畸变能增加，使得复合材料处于线性硬化的阶段。随后真应变继续增加，流变应力的增幅却变缓，说明复合材料出现了软化现象，但加工硬化的作用仍然强于软化的作用，使流变应力的综合效果依旧呈上升趋势。当变形温度一定时，随着应变速率增大，流变应力整体呈增大的趋势。当变形温度为700 ℃时，真应力-真应变曲线呈典型的动态回复型。当变形温度为750 ℃以及800 ℃时，动态回复过程缩短，随后进入稳态阶段，随着真应变的增大，流变应力的数值几乎不再变化。当应变速率为0.100 s-1和0.010 s-1时出现一段典型的动态再结晶曲线，即流变应力快速上升到一个峰值，而后发生动态再结晶，使材料软化，流变应力减小，继续变形，再结晶的软化作用减弱，流变应力增加，但流变应力始终在缓慢增加[10]。当变形温度为850 ℃、应变速率0.001 s-1时，从图2（d）中可看到流变应力随着应变的增加而快速达到一个极值，随后随着应变的增加而减少，最后趋于平缓，这是典型的动态再结晶曲线，说明复合材料在较高温度、较低应变速率下发生了动态再结晶行为。

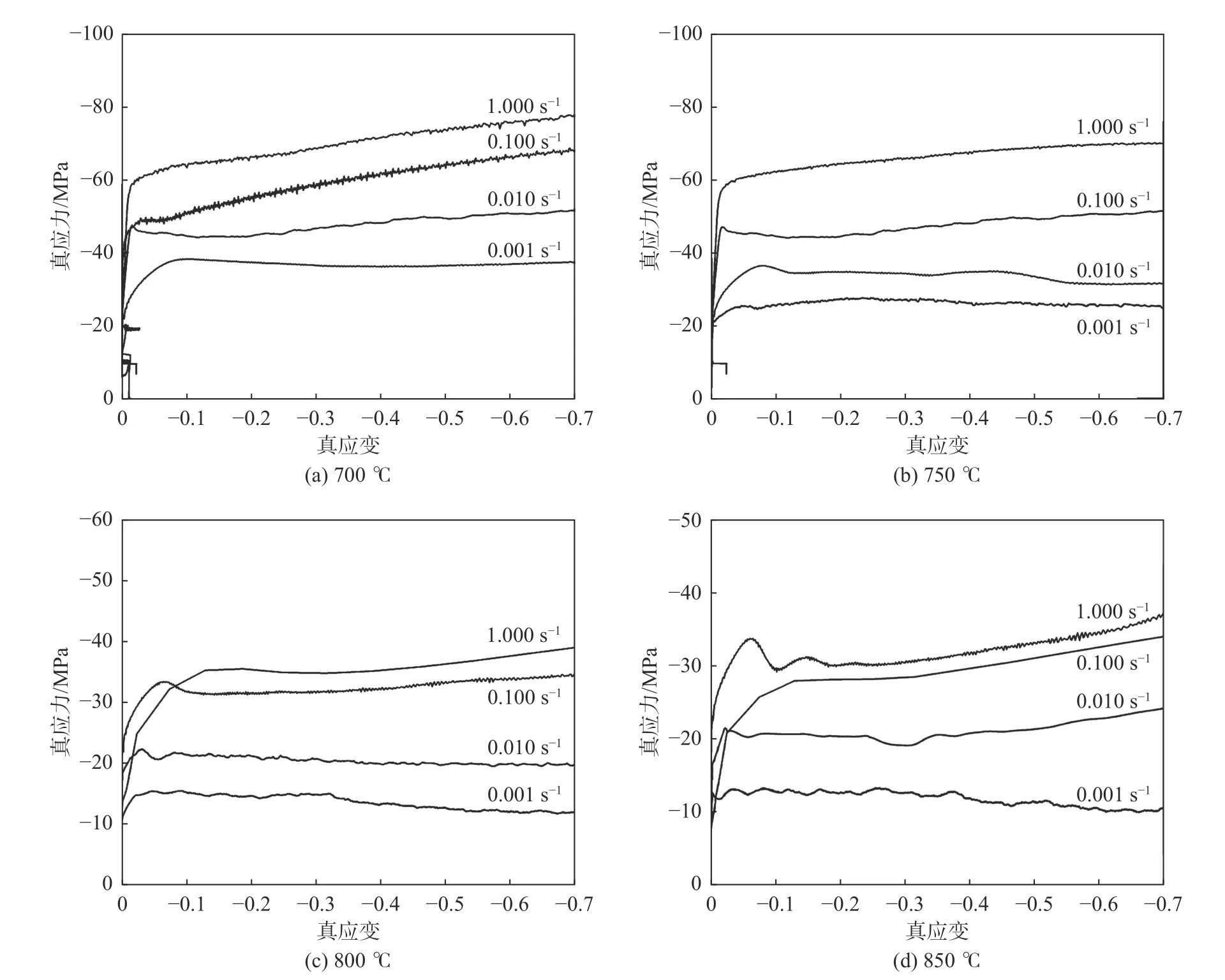
图2 铜/石墨复合材料在不同温度不同应变速率下的真应力-真应变曲线Fig.2 True stress-strain curves of copper/graphite composites at different strain rates

2.3 本构方程

在高温变形过程中，材料的成分基本不会变化[11]，对于高温热变形下流变应力主要的影响因素是应变速率和变形温度。根据Carofalo 公式[12]，温度和应变速率对施加应力的影响可以用以下方程来充分表示：

式中：A 为结构因子；α 为应力常数；n 为应力指数；β 为应力水平参数。A、α、n、β 为与应变温度无关的材料参数。R 为摩尔气体常数，一般取8.314 J/mol；Q为活化能；T为温度；为应变速率；σ为流变应力。公式（1）适用于低应力水平（ασ ＜0.8）；公式（2）适用于高应力水平（ασ ＞1.2）。公式（3）适用于所有情况下的高温流变应力情况。

而描述高温流变应力的常用函数是Zener-Hollomon（Z）参数[13]：

因此，根据上述公式[14]，通过材料常数便可计算任意情况下的高温流变应力的变化情况。应变速率是影响材料流变应力最重要的参数之一，当变形温度不变时，应变速率的增大使得复合材料的流变应力增大，可得到该材料为正应变速率敏感性材料。将公式（1）～（3）两边同时取对数可得：

由公式（9）～（11）可知，当温度T一定时，lnσ曲线、曲线和ln ε˙-ln[（sinh（ασ）]曲线均呈线性关系。分别将不同变形条件下的最大流变应力和对应的应变速率带入，并对它们进行一元线性回归处理，得到的结果如图3 所示。由结果可知，每个线性回归得到的相关系数均大于0.95，说明应变速率和流变应力之间高度相关。

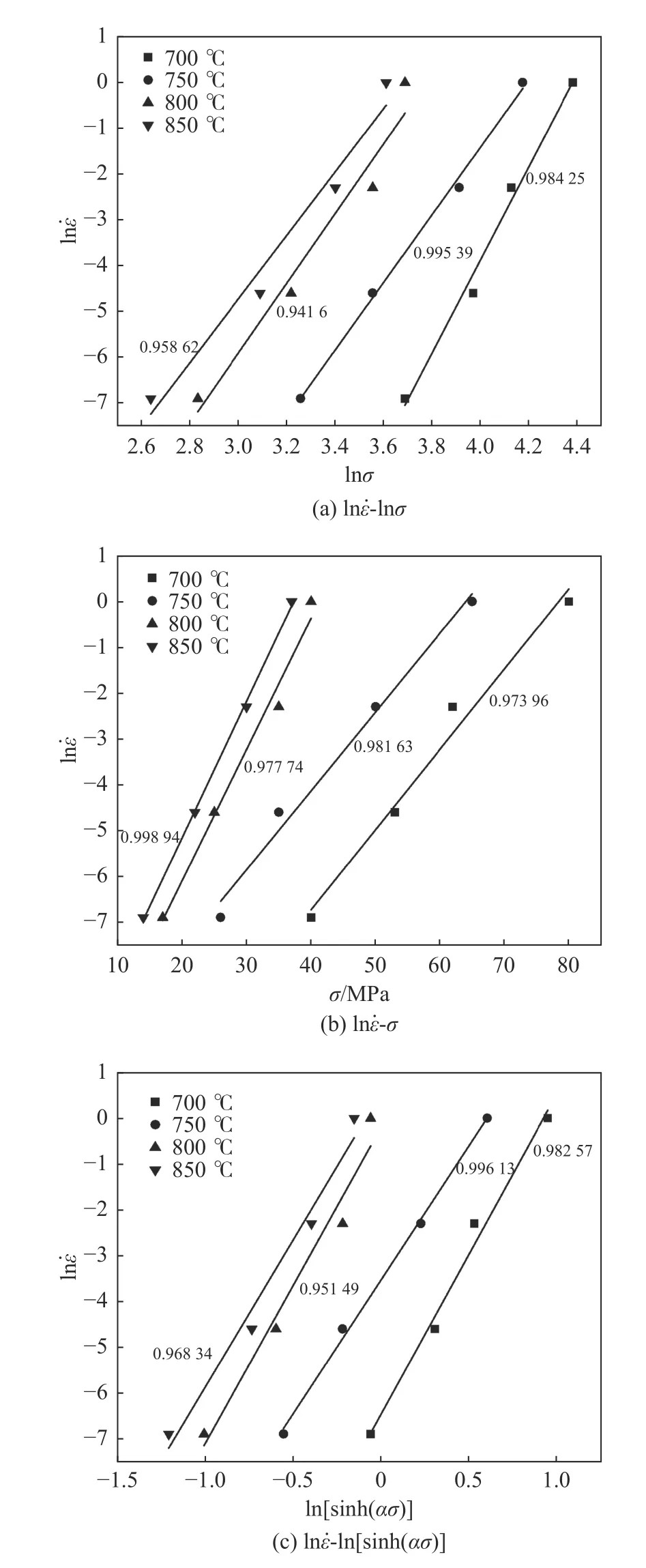
图3 应变速率与复合材料流变应力的关系图Fig.3 Relationship between strain rate and flow stress of composites material

β、n1、n 分别是[sinh（ασ）]的斜率。将复合材料的最大应力与应变速率代入上述公式（9）、（10），然后画出的关系图，并对它们进行一元线性回归，结果如图3（a）及（b）所示。公式（9）要求处于高应力状态，因此由700、750 ℃斜率的平均值得到β 约为0.174，而公式（10）用于低应力状态，由800、850 ℃时斜率的平均值得到n1约为8.228，而α=0.021。然后将α、σ的值代入公式（11），并进行一元线性回归，绘制的图如图3（c）所示，对斜率取平均值，得到n 约为7.108。

对真应力-真应变曲线分析可知，变形温度对流变应力的变化有着重要的影响。为了得到变形温度和流变应力之间的关系式，我们对公式（5）两边取对数得到如下关系式

经等式两边变形得到

然后将复合材料的最大应力与绝对变形温度代入公式（14），进行一元线性回归后得到图4。由图4 可知，流变应力的双曲正弦函数的对数与绝对温度的倒数之间满足很好的线性关系。

图4 ln[sinh（ασ）]与绝对温度倒数的关系图Fig.4 Relationship between ln[sinh（ασ）] and reciprocal of absolute temperature

取图4 中斜率的平均值7.835，即D=Q/（1 000nR）=7.835，而理想气体常数R 为8.314 J/mol，代入计算可以得到高温压缩热变形激活能Q=1 000DnR，为463.02 kJ/mol。将Q、T和代入公式（4），得到的lnZ参数的数值如表1 所示。

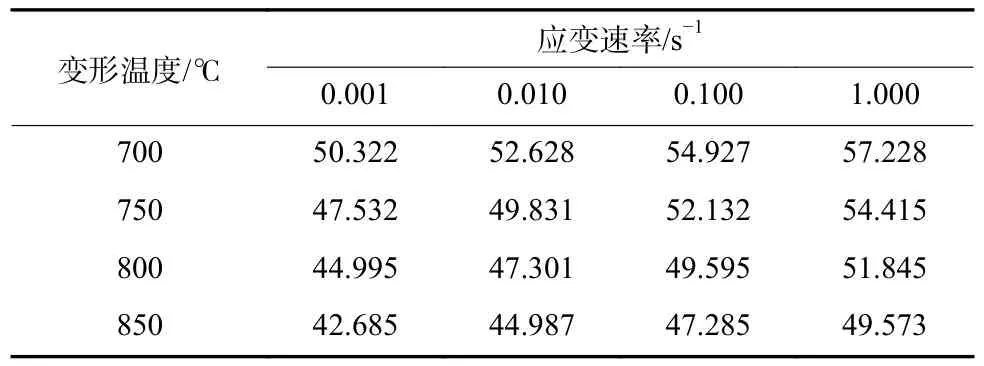
表1 不同变形温度、应变速率下的lnZ 的数值Tab.1 LnZ under different deformation temperature and different strain rate

对公式（5）取对数

将表1 中的lnZ和对应的最大应力值代入公式（15），并进行最小二乘法线性回归，得到的结果如图5 所示。由图5 可知，Z参数的对数值和最大应力的双曲正弦函数的对数值线性相关性很高，相关度为0.983 29。从图5 中可以得到斜率n 为7.89，这与前述得到n 的7.108 很相近，因此取n=7.89 进行后续的计算，且可以得到截距值为51.08，即lnA=51.08，求得A 为1.53×1022，将A、n、Q代入公式（4）得

图5 lnZ-ln[sinh(ασ)]的关系图Fig.5 Relationship between lnZ and ln[sinh(ασ)]

或者按公式（8）表示为

为了验证公式（17）的正确性，我们将铜/石墨复合材料的不同变形温度、应变速率代入公式（17），将求得的理论最大应力值与试验的最大应力值进行比较，并对比两者误差的大小，结果如图6 所示。铜/石墨复合材料最大应力的计算值和试验值的误差在9.5%以内，说明两者吻合的较好。

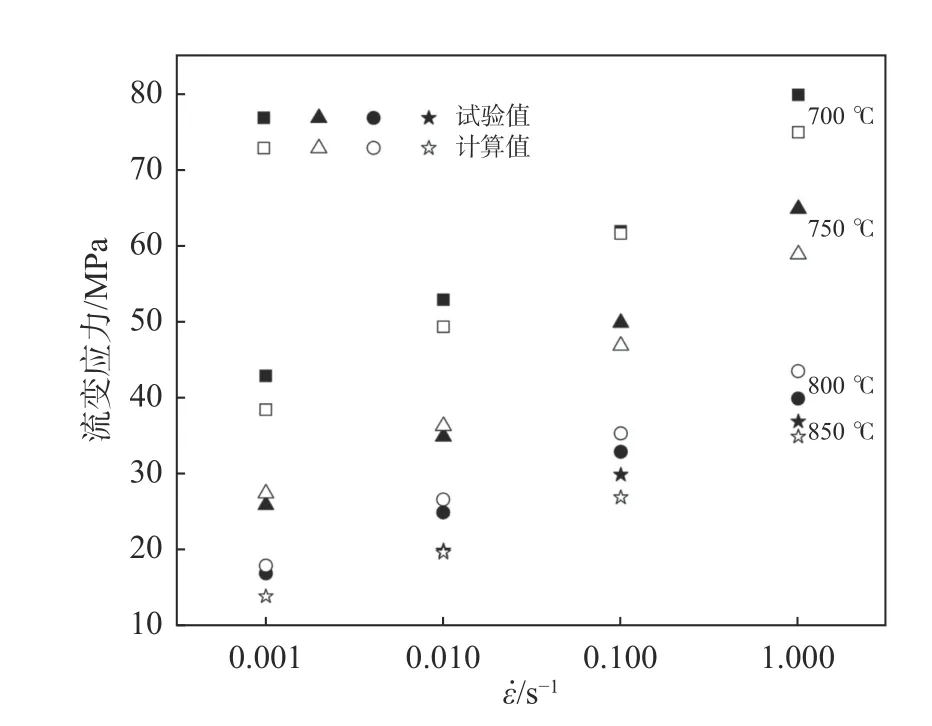
图6 最大应力的计算值和试验值的对比图Fig.6 Comparison of the calculated value and test value of the maximum stress

2.4 变形条件对组织性能的影响

图7 是铜/石墨复合材料在相同变形速率（0.100 s-1），不同变形温度（700、750、800、850 ℃）时的金相组织图。从图7 中可以看出，在应变速率为0.100 s-1时，当变形温度比再结晶温度高时，复合材料发生了明显的动态再结晶现象，当变形温度不断提升时，提供动态再结晶的能量也越多，促进了晶界的不断迁移，再结晶晶粒长大越严重，晶粒结构也发生了明显粗化。

图7 不同温度下复合材料的金相组织Fig.7 Metallographic structure of composites materials at different temperatures

2.5 热加工图

热加工图是一种重要的研究方法，可以建立起金属在热变形过程中能量耗散与微观组织演化之间的关系。通过分析各个加工区域的微观变形机制，有效地避开失稳区，从而达到材料组织性能控制的目的。

材料的热加工过程可以看成一个封闭的热力学系统，在热变形过程中的材料可以看做一个能量耗散体[15]，外部提供总能量用P来表示，它由两部分组成，分别是耗散量G（塑性变形消耗的能量）以及耗散斜量J（塑性变形时组织演变消耗的能量），耗散总功率公式如下[16]：

G和J的分配比例通常由应变速率敏感系数m 来确定：

式中：K是与应变速率无关的常数。将公式（20）代入公式（18）和（19），可得到

m的值通常位于0 和1 之间，当m=0 时表明热加工过程中不会有能量的耗散；当m=1 时，J 达到最大值Jmax。通常引入功率耗散因子η来描述材料内部微观组织演变消耗能量的占比。

即

功率耗散因子η的值越大，并不代表材料的热加工性能越好，在失稳区的η值也有可能很高，所以需要先对材料进行塑性失稳判断。

失稳图是为了弥补能量耗散图的不足。失稳的判据通常由下式来表示：

因此，要想得到热加工的安全区域，必须先求出应变速率敏感系数m，进而求出η。

采用三次样条差值法[17]求解m，对lnσ和之间的关系进行三项式拟合计算，得到的拟合图如图8 所示，由此可得到三次样条差值函数的系数a、b、c、d，然后根据计算式m=b+2cln ε˙+3d（ln ε˙）2，求得m，m/（m+1），ln（m/m+1），功率耗散因子η=2m/（m+1）。

图8 三次样条差值法拟合曲线Fig.8 The fitting curves by cubic spline difference method

图9 是根据上述得到的参数绘制出的铜/石墨复合材料的耗散图。当η＞0.6 时，一般为材料的开裂区或是超塑性区；当η位于0.30～0.55 之间时，一般是典型的再结晶区，而当η＜0.3 时，一般是不安全区。由图9 可知，当变形温度为780～820 ℃，应变速率为0.540～1.000 s-1之间，以及变形温度为830～850 ℃，应变速率为0.001 s-1左右时，功率耗散系数η的值在0.3 以上，表明这些区域用于复合材料内部组织转变的功率较多，可能为铜/石墨复合材料良好的加工区域。

图9 铜/石墨复合材料的功率耗散图Fig.9 Power dissipation diagram of copper/graphite composites

绘出失稳图，则需要失稳判据的数值，同样采用三次样条差值法，保持变形温度和变形量不变，对ln（m/m+1）和ln之间的关系进行三项式拟合计算，由此得到系数a1、b1、c1、d1，求得η=b1+2c1ln+3d1（ln）2。

图10 是由铜/石墨复合材料的热加工图[18]。由图10 可知，铜/石墨复合材料的最适宜的加工区域是780～820 ℃，变形速率为0.050～0.100 s-1；830～850 ℃，应变速率为0.001～0.004 s-1之间，由此可知，热加工图为铜/石墨复合材料高温下的塑性变形的设计以及实际应用提供了理论依据和参考。

图10 热加工图Fig.10 Thermal processing map

3 结论

（1）变形温度和应变速率对铜/石墨复合材料的真应力-真应变曲线的影响很大，当应变速率一定时，随变形温度的升高，流变应力减小，当变形温度一定时，随应变速率变大，流变应力整体呈增大的趋势。当应变速率为0.001 s-1，变形温度为750、800、850 ℃时，真应力-真应变曲线呈动态回复的特点；在其他变形条件下，流变应力最终并没有进入稳态阶段，而是随应变的增加而缓慢增加。

（2）在描述铜/石墨复合材料的流变应力与应变速率、变形温度的函数关系中，双曲正弦函数很好的描述了它们之间的关系，并由此求得的材料常数、热应变激活能以及本构方程如下所示：

α=0.021，β=0.174，n=7.89，Q=463.02 kJ/mol；

本构方程：

并根据构建的本构方程验证了最大应力的吻合性，发现计算值和试验值的误差在9.5 %以内，吻合性很高。

（3）综合考虑铜/石墨复合材料的耗散图及热加工图可知，变形温度为830～850 ℃，应变速率为0.001～0.004 s-1为适宜的热加工工艺参数。