曲线段地铁运行对某体育馆振动影响预测分析

左汉文,赵志亮,杜 浦

(1. 中国电子工程设计院股份有限公司,北京 100840; 2. 广州大学 土木工程学院,广东 广州 510006;3. 郑州阿特美特节能技术有限公司,河南 郑州 450018)

0 引言

近年来,随着城市轨道交通的发展建设,地铁列车运行所引起的周边环境振动问题,正在被广泛关注,若线路下穿一些年代较为久远的历史优秀建筑,地铁列车对其的振动影响,也正在成为困扰城市轨道交通发展建设的一项重要难题[1-2]。目前,越来越多的学者针对上述问题正在进行深入研究,孙晓静[3]以北京地铁4号线成府路站及南北区间工程为背景,研究了地铁列车的振动特性、场地背景振动规律、特殊减振措施的减振性能、周边振源对环境的振动影响等。袁扬等[4]根据实测数据,研究发现在距离隧道中心线50 m范围之内,水平振动强度是竖向振动强度的2～4倍。韩广森[5]、孟照博[6]和马蒙[7]研究了城市轨道交通引起的环境振动对古建筑的影响。李克飞等[8],孙晓静等[9]对普通道床及不同形式减振道床的减振效果进行了实测与研究。一直以来,小曲线半径地铁列车振源下穿已建历史保护名录建筑的实际工程十分罕见,针对此类工况的振动影响评估研究极为稀少。

本文基于郑州地铁7号线下穿某体育馆项目背景,结合已经通车的地铁5号线隧道内与地面处振动同步实测结果,获得振动源强数据以及有限元模型校核参数依据;同时对体育馆楼内与楼外地面进行实测对比分析,获得体育馆楼内外传递关系;最终通过有限元计算预估地铁7号线对体育馆地面处振动响应,结合楼内外传递规律,最终预估楼内敏感点位置的振动响应。

1 项目简介

1.1 体育馆与地铁线路位置关系

该体育馆主体结构类型为钢筋混凝土框架结构和砖混混合结构,屋盖为钢结构,基础类型为三七灰土条形基础,地上3层。该建筑建于1966年,为郑州市近现代优秀建筑,现已使用55 a,已超过50 a的设计使用年限。郑州地铁7号线采用6辆编组A型车,该区间设计时速80 km/h,隧道双线下穿体育馆,下穿处隧道与体育馆基础最小竖向净距26.89 m,隧道埋深约29.39 m,最小曲线半径R=450 m,具体线路关系如图1和图2所示。

图1 体育馆与地铁线路平面关系图Fig. 1 Plan relationship between the gymnasium and Metro Line

图2 体育馆与地铁线路剖面关系图Fig. 2 Cross section relationship between the gymnasium and Metro Line

1.2 体育馆容许振动标准

本项目评估的体育馆建设年代久远,在2018年被收录在郑州市第一批历史建筑保护名录。因此本项目容许振动标准参考GB 50868—2013《建筑工程容许振动标准》[10]中表7.1.2交通振动对建筑结构影响在时域范围内的容许振动值中对振动敏感、具有保护价值、不能划归上述两类的建筑指标执行。

1)顶层楼面中心位置处水平向在1～100 Hz容许振动速度峰值≤2.5 mm/s;

2)基础处竖向和水平向在1～10 Hz容许振动速度峰值≤1.0 mm/s、在50 Hz容许振动速度峰值≤2.5 mm/s在100 Hz容许振动速度峰值≤3.0 mm/s。

2 体育馆原位背景振动测试

原位背景测试的研究目的是了解既有建筑背景环境振动现况,对比室外地面振动测点实测数据,研究振动评估点与楼外地面振动传递关系。本章节共对多个区域进行背景振动测试,各区域测点编号如表1所示。

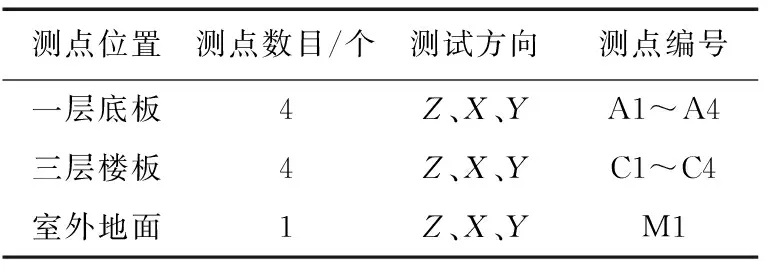
表1 测点分布表Table 1 Measurement points distribution table

每组测点同时采集竖直向Z、垂直地铁线路运行方向的水平向X、沿地铁线路运行方向的水平向Y振动速度数据。

具体测点布置如图3所示,现场实景照片如图4所示。

图3 体育馆测点布置图Fig. 3 Layout plan of measuring points in the gymnasium

图4 体育馆测点实景照片Fig. 4 Photos of measuring points in the gymnasium

本项测试对各测点进行1/3倍频程频域分析,采样频率256 Hz,分析频率100 Hz,FFT分析点数1024点,采样时间200 s,窗函数为汉宁窗、重叠系数3/4。通过实测分析,一层最大振动速度响应点为A1、三层最大振动速度响应点为C1,最大响应测点详细分析结果如图5所示。

图5 体育馆各测点振动速度分析图Fig. 5 Analysis chart of vibration velocity at each measurement point in the gymnasium

结合体育馆内外实测结果,对比获得传递函数曲线如图6所示。

图6 体育馆基础与地面振动速度比值Fig. 6 Ratio of vibration velocity between the foundation of the gymnasium and the ground

3 轨道交通7号线振源模拟测试

由于郑州轨道交通7号线一期工程尚未建设通车,故需要选取一条已经通车运行铁路,选取一近似断面在隧道内进行振动测试,以了解通过针对不同轨道交通轨道采取减隔振措施所达到的减振效果,为本项目最终测试结论及解决措施提供参考依据。本项目最终选取已经通车运行的郑州轨道交通5号线进行类比振源模拟测试。

3.1 模拟线路对比

类比测量时选择的线路应满足条件相同或相似:地质条件、车辆类型、列车速度、轨道结构形式、直/曲线半径、隧道结构和断面等。本项目最终选取已经通车运行的郑州地铁5号线进行类比振源模拟测试。类别条件对比如表2所示。

表2 测试断面对比信息表Table 2 Comparison information table of test sections

3.2 隧道内实测结果

其中每组断面共布置2个测点,布置在轨面上方1200 mm隧道壁位置,其中1#测点采集竖直向振动数据、2#测点采集垂直线路运行方向的水平向振动数据,具体测点布置及现场照片如图7和图8所示。

图7 隧道内测点布置图Fig. 7 Layout of measurement points inside the tunnel

图8 地铁5号线隧道内测点实景照片Fig. 8 Photos of measurement points inside the tunnel of Metro Line 5

本项测试对各测点进行振动速度1/3倍频程频域分析,采样频率2048 Hz,分析频率1000 Hz,FFT分析点数1024点,每组采样时间60 s,分析时长为过车影响时段6 s,窗函数为汉宁窗、重叠系数3/4,测点分析结果如图9所示。

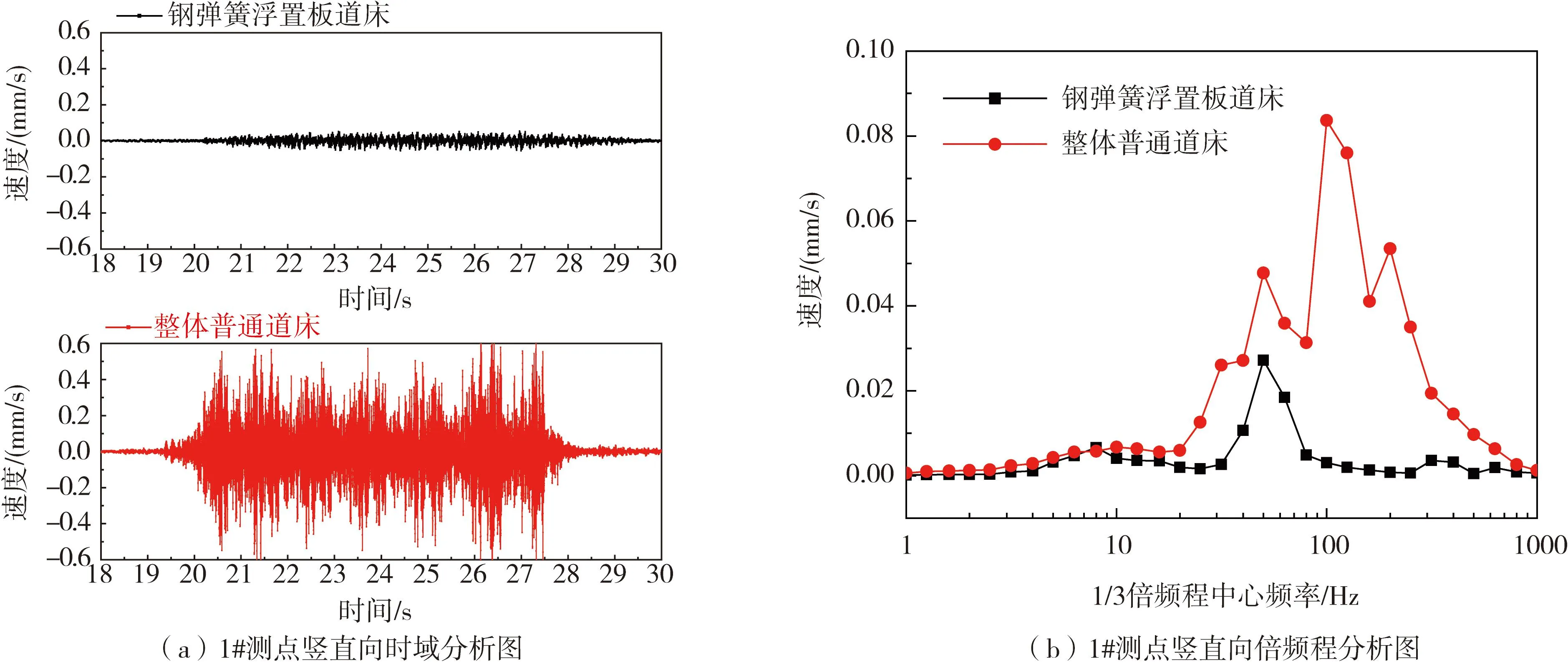
图9 地铁5号线隧道壁测点振动速度分析图Fig. 9 Analysis of vibration velocity at measurement points on the tunnel wall of Metro Line 5

3.3 地面位置实测结果

本项测试测点布置在姚砦站～众意西路站站区间上部地面位置,布置1个测点,布置在轨面上方地面位置,同时采集竖直向及垂直线路的水平向振动数据,具体测点布置及现场照片如图10所示。

图10 地铁5号线地面测点实景照片Fig. 10 Photos of ground measurement points on Metro Line 5

本项测试对测点各方向进行振动速度1/3倍频程频域分析,采样频率256 Hz,分析频率100 Hz,FFT分析点数1024点,每组采样时间60 s,分析时长为过车影响时段6 s,窗函数为汉宁窗、重叠系数3/4,测点分析结果如图11所示。

图11 地铁5号线地面测点振动速度1/3倍频程频谱图Fig. 11 The 1/3 octave frequency spectrum of vibration velocity at ground measurement points on Metro Line 5

4 体育馆土体有限元计算

基于普通整体道床与钢弹簧浮置板隧道壁振动实测结果为体育馆土体模型计算振源进行输入,基于地面位置处振动实测结果,校核体育馆土体有限元模型计算结果,最终结合体育馆楼内外传递函数推导地铁通车后体育馆建筑内评估点振动响应。

本章节振源模拟采用的激励输入为实测已经通车的郑州市轨道交通5号线区间隧道壁振动加速度响应。计算步骤为首先对隧道壁位置进行单点激励,计算地面位置响应,再计算两点之间传递函数,最后根据实测隧道壁结果推导地面位置实际振动响应。

4.1 模型建立

数值仿真模型的建立需要综合考虑边界条件对仿真结果的影响,为避免边界条件对仿真结果的影响,所建模型尺寸应该尽量大,然而过大的模型需要较高的计算资源。根据理论研究和工程经验,当模型尺寸是分析对象特征尺寸的3～5倍时,即可满足计算精度。根据拟定的仿真分析内容,本报告建立轨道交通5号线土体数值仿真分析模型尺寸为80 m×80 m×80 m,隧道埋深15.2 m,如图12所示。

为减少因模型截取而引起的边界调节误差,本报告中在土层边界及底部边界施加黏弹性边界条件[11]:

正应力方向:

(1)

(2)

式中:G为每一层土体的剪切模量;Cp和Cs分别为土体的压缩波速和剪切波速;ρ为土体密度;R为边界至振源的距离;CBN为正应力方向的阻尼;KBN为正应力方向的刚度;CBT为剪应力方向的阻尼;KBT为剪应力方向的刚度。

4.2 模型计算分析

通过姚砦站-众意西路站区间隧道壁与地面实测数据,将实测结果与有限元分析结果在不同频率范围地面振动响应振动速度幅值进行校核,具体校核结果如图13所示。

图13 地面位置振动速度1/3倍频程校核曲线Fig. 13 Ground position vibration velocity 1/3 octave calibration curves

模型经过校核后,结合表2,将隧道上部土体埋深由15.2 m增至29 m。本次仿真输入激励分别为:普通整体道床、钢弹簧浮置板道床隧道壁的竖直向及垂直线路运行方向的水平向振动数据,具体激励曲线见3.2节。建立轨道交通7号线土体数值仿真分析模型尺寸为80 m×80 m×80 m,隧道埋深29 m,如图14所示。

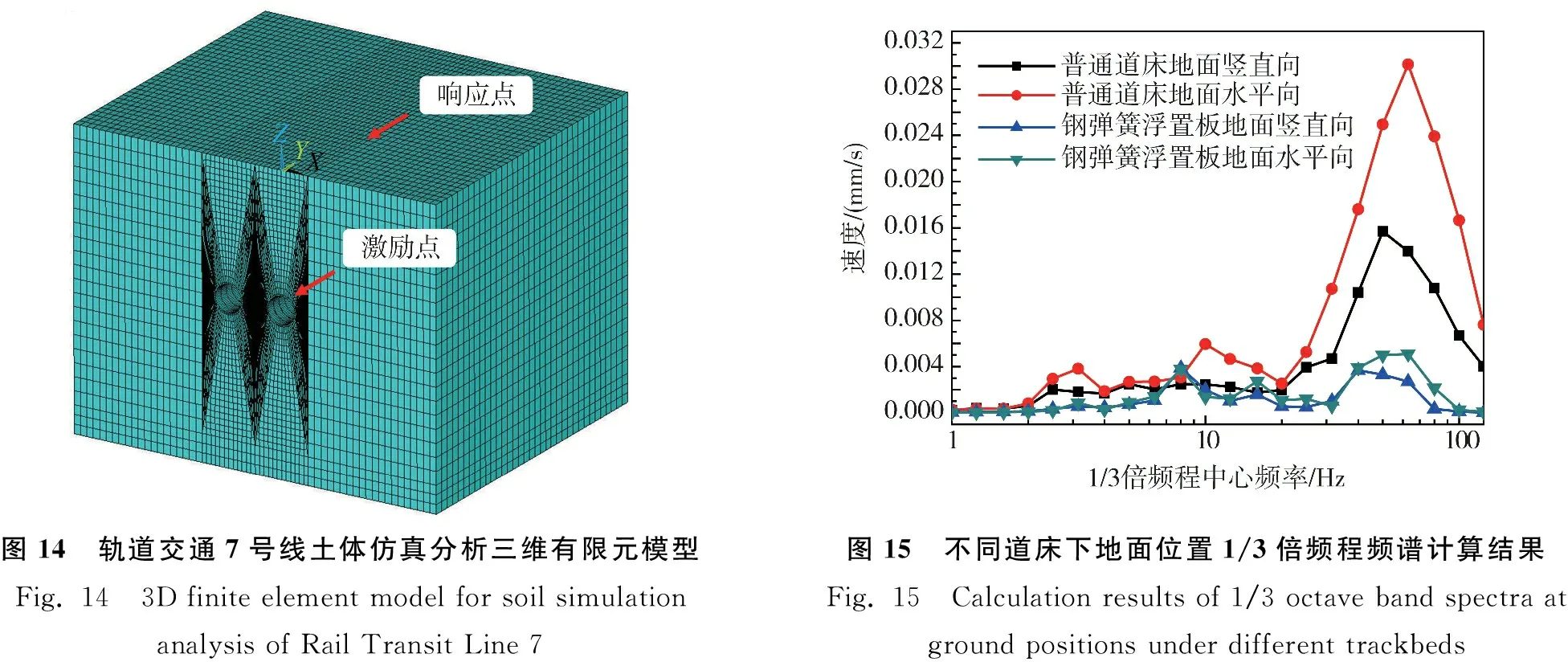
图14 轨道交通7号线土体仿真分析三维有限元模型Fig. 14 3D finite element model for soil simulation analysis of Rail Transit Line 7 图15 不同道床下地面位置1/3倍频程频谱计算结果 Fig. 15 Calculation results of 1/3 octave band spectra at ground positions under different trackbeds

输入实测隧道壁的振动激励,可计算郑州轨道交通7号线运行时轨道交通上方地面位置振动数据,其计算结果如图15所示。

结合体育馆楼内外传递函数对体育馆顶层及基础处振动速度进行推算。普通整体道床及钢弹簧浮置板道床车辆运行工况下振动速度1/3倍频程频域分析曲线如图16所示。

图16 不同道床下体育馆1/3倍频程频谱计算结果Fig. 16 Calculation results of 1/3 octave band spectra of gymnasium under different track beds

对比GB 50868—2013《建筑工程容许振动标准》[10]中所示容许振动标准,分析后得到不同道床下体育馆各位置振动速度峰值,具体统计结果如表3所示。

表3 不同道床下体育馆振动速度峰值统计Table 3 Peak vibration velocity statistics of gymnasium under different track beds

根据表3数据判断,当轨道交通7号线选用普通整体道床下穿体育馆时,列车引起的水平向振动在体育馆顶层楼面预估放大至4.50 mm/s,超过2.5 mm/s控制标准,而采用钢弹簧浮置板道床形式,体育馆基础预估振动为0.04 mm/s,顶层楼面预估振动为1.36 mm/s,均满足建筑容许振动标准。

5 结语

通过对体育场建筑实测分析、类比线路隧道壁及地面振动实测分析,以及体育场土体模型计算分析,结果表明:

1)相对室外地面而言,体育馆基础位置振动速度放大最大频率点出现在垂直线路运行方向的水平向50 Hz,振动速度幅值放大比例为2.98倍,顶层位置振动速度放大最大频率点出现在垂直线路运行方向的水平向80 Hz,振动速度幅值放大比例为5.27倍。

2)普通道床隧道壁竖直向1/3倍频程最大振动速度幅值为8.36×10-2mm/s,对应中心频率点为100 Hz,水平向1/3倍频程最大振动速度幅值为1.29×10-1mm/s,对应中心频率点为100 Hz;钢弹簧浮置板道床隧道壁竖直向1/3倍频程最大振动速度幅值为1.00×10-2mm/s,对应中心频率点为50 Hz,水平向1/3倍频程最大振动速度幅值为2.72×10-2mm/s,对应中心频率点为100 Hz。

3)曲线段普通道床地面位置水平向1/3倍频程最大振动速度幅值为3.01×10-2mm/s,竖直向为5.08×10-3mm/s,钢弹簧浮置板道床水平向为3.87×10-3mm/s。

4)若采用普通整体道床,地铁列车通过时体育馆顶层楼面振动速度峰值预估为4.50 mm/s,超过标准2.5 mm/s限制,若采用钢弹簧浮置板道床,竖直向与水平向均可满足建筑容许振动标准。