核心素养导向下的小学数学大单元教学
——以人教版数学教材五年级上册“小数除法”单元为例
2024-01-02杨驰
杨 驰
(广东省广州市越秀区登峰小学)
在小学数学学科教学中,一般以“单元”为目标,分“课时”进行,教师在教学中较少关注不同单元间的联系,通常会忽略不同单元内容之间的整合。这样的教学活动不利于帮助学生知识体系的建构,不利于培养学生的核心素养。因此,为了帮助学生构建完善的知识结构,教师需要先构建大单元教学,将原本分散的知识进行整合。学生通过经历建构完整知识体系的过程,不仅能系统地掌握这一模块知识,实现知识体系的构建,还能有效降低学习难度,提升学习的积极性和学习效果。本文以人教版数学教材五年级上册“小数除法”单元为例,从以下三个方面谈谈核心素养导向下的小学数学大单元教学。
一、单元知识内容整体分析
小学数学教材的编排总体上是按照从低到高、从易到难的结构设计的。因此,在进行大单元教学的过程中,教师要将一个或多个单元的内容进行梳理,化零为整,确保学生的学习内容具备结构性和层次性。以教学“小数除法”为例,这部分内容与“小数的意义”“整数除法”“小数乘法”等知识是紧密联系的。教师需要仔细分析这些内容之间的联系,在发展运算能力这一核心素养目标下进行单元整体设计教学,引导学生发现小数除法在不同问题背景下知识内容间的内在联系。下面,笔者从两个方向谈谈单元知识内容整体分析。
(一)横向重组,精练单元整体架构
下图是对“小数除法”单元例题的分析整理。本单元有“除数是整数的小数除法”“一个数除以小数”“商的近似数”“循环小数”“用计算器探索规律”和“用进一法和去尾法解决问题”六个教学模块。这些知识都是从生活需要的角度出发,创建有趣的问题情景,探究算理,“循理入法,以理驭法”。
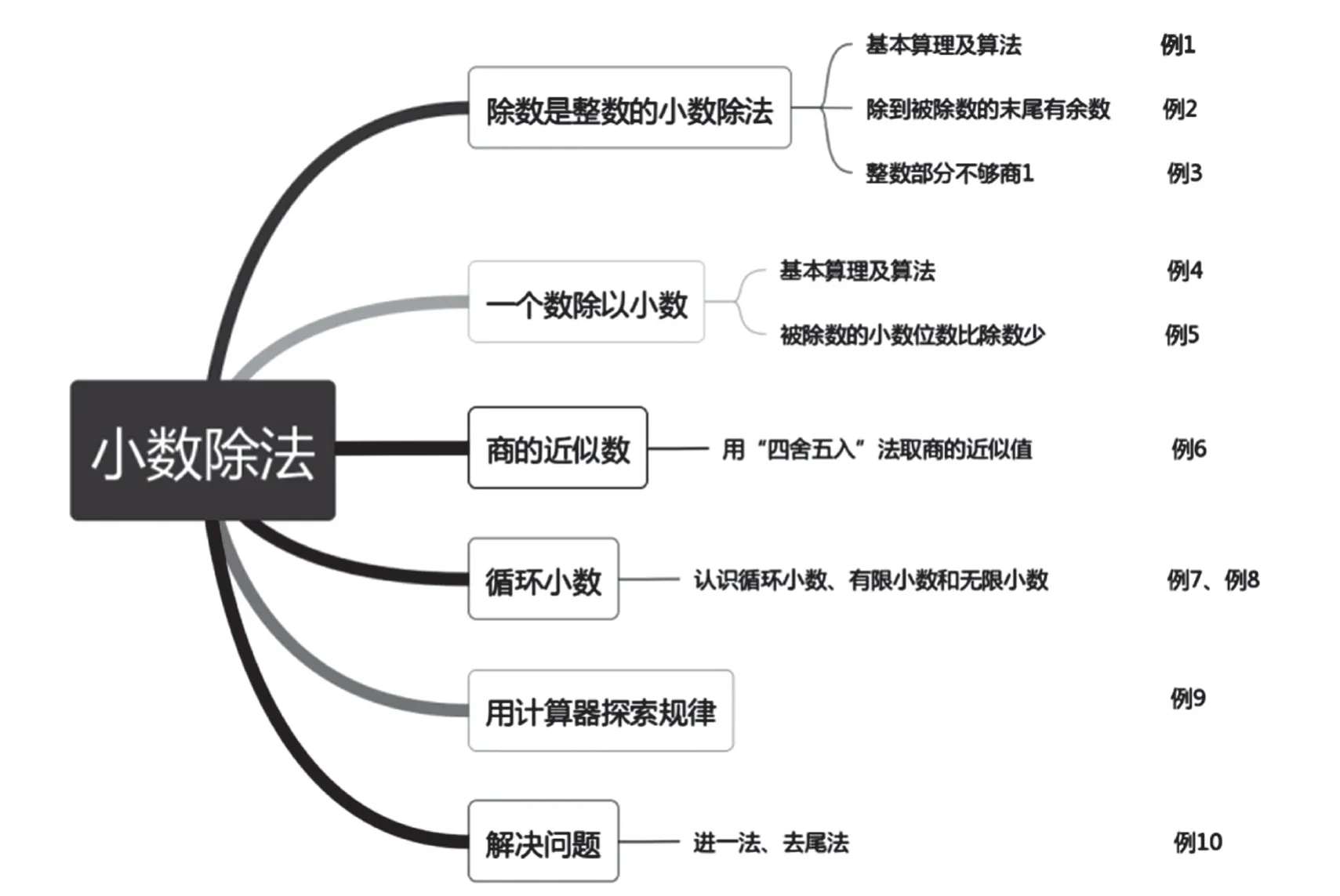
(二)纵向拓展,构建不同单元间的联系
学生在学习“小数除法”之前,已经学习了“小数”和“除法”两个模块的基础知识,对应的知识体系如下图所示。从除法的角度分析发现,“表内除法”和“有余数的除法”是整个除法运算的基础,“除数是一位数的整数除法”和“除数是两位数的整数除法”是除法运算的核心,这两部分内容又是学习“小数除法”的基础;从小数的角度分析发现,理解小数的意义是理解小数除法算理的基础。教学中可结合整数除法和小数的意义这两部分的知识,引导学生运用迁移、转化、推理的数学思想方法进行小数除法的学习。

二、单元知识内容结构化整合
2022 年版课标提出:“设计体现结构化特征的课程内容”“课程内容的组织,重点是对内容进行结构化整合,探索发展学生核心素养的路径”。教师在进行“小数除法”单元整体设计时,应围绕发展运算能力这一核心素养目标,引导学生发现在解决小数除法不同问题时知识间的联系。
本单元有六个教学模块,能否从单元整体设计的角度,对单元的教学内容进行结构化整合,沟通小数除法与整数除法之间的联系,疏通单元内部知识点的脉络,我做了如下尝试。如下图所示,本单元的知识都是围绕除法算式中的“除数”和“商”两个部分展开的。“除数是整数的小数除法”是本单元的起点,“一个数除以小数”其实是“除数是整数的小数除法”的变式,其他知识都围绕这两种小数除法展开并逐步深入。这部分的主要目标是:理解两种小数除法的算理,掌握算法。第二部分是围绕商展开,在掌握计算小数除法的基础上,认识商的一种特殊形态——循环小数,并用计算器探索商的规律,根据实际情况用四舍五入法、进一法和去尾法取商的近似数。
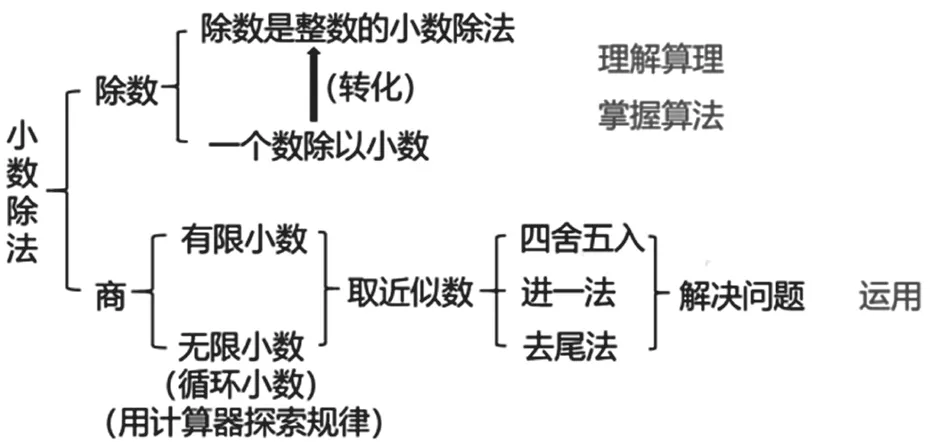
基于以上分析,我对“小数除法”的单元教学进行了整合,如下表所示,将新课教学分成两大板块。第一个板块是计算板块,包括了“除数是整数的小数除法”和“一个数除以小数”。第二个板块是运用板块,包括“循环小数及”“用计算器探索规律”和“商的近似数”,把“商的近似数”放到“循环小数”和“用计算器探索规律”之后,把三种求商的近似数方法放进同一教学板块。

三、设计有效的教学活动
大单元教学背景下,设计有效的课堂教学活动能引导学生发现并理解新旧知识间的联系与区别,构建完整的知识体系,高效地实现课堂教学目标。下面从新授课、练习课和单元复习课这三种常见的课型进行分析。
(一)新授课
在新知的学习中,教师要引导学生发现新旧知识之间的联系与区别,关注知识转化和迁移的过程,帮助学生构建完整的知识体系。
1.不同单元间新旧知识的过渡
将已学的其他单元旧知迁移到本单元新知的学习中。
案例一:在教学单元起始课“除数是整数的小数除法”时,通过对比除数是整数的小数除法与整数除法,引导学生理解这两种不同的除法的算理本质相同,都是“用几个计数单位去除以除数”;算法本质也相同,都是“除到被除数的哪一位,就把商写在那一位的上面”。不同点是,“除数是整数的小数除法”要定位商的小数点,如果除到个位有余数还要用更小的计数单位继续除;而整数除法不用考虑小数(点),如果除到个位不再继续除。如下表所示。

案例二:在教学“用进一法和去尾法解决实际问题”中,通过导入二年级的有余数的除法解决问题,引导学生发现新旧知识的知识背景相同,都是处理解决问题中的剩余部分。不同点是,一个是对余数进行处理,一个是对商的小数部分进行处理。如下表所示。

2.单元内新旧知识的过渡
将已学的本单元旧知迁移到本单元后续新知的学习中。
案例:在教学“一个数除以小数”时,教师尝试调整了例题的情境和数据,如下表所示。调整前的原式是7.65÷0.85,转化后是765÷85,变成了整数÷整数。计算一个数除以小数最关键的是要把除数转化为整数,而被除数仍然可能是小数。调整后可以避免受无关信息的干扰,便于学生更有效地利用新旧知识之间的联系进行迁移从而掌握算法:把除数转化为整数。

(二)练习课
在练习课的教学中,教师要引导学生进一步沟通新旧知识之间的联系,深化认知,帮助学生构建完整的知识体系。
案例一:在教学“除数是整数的小数除法”练习课时,练习教材第27 页第12 题,教师引导学生回忆商不变的性质,为随后学习一个数除以小数做了很好的提示与承接,不仅将新授的知识与前面的内容串联起来,而且还为下一节学习新知做了铺垫。

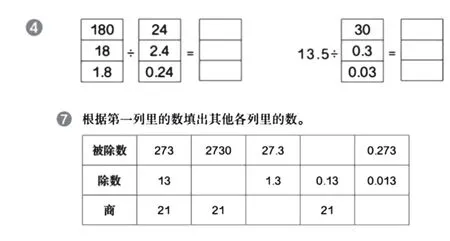
案例二:在教学“除数是整数的小数除法”练习课时,练习教材第30 页第4 题和第31 页第7 题。通过练习第4 题左边的表和第7 题,有助于学生深入体会并理解商不变的性质在小数除法中的应用;通过练习第4 题右边的表格,有助于学生深入体会并理解商的变化规律在小数除法中的应用。系统的练习能将新知与旧知的内容串联起来,有助于学生构建知识体系。
(三)复习课
教师备课时一般按照从整体到部分再到整体的思路进行单元整体设计,在完成单元新知部分教学后会安排复习课,引导学生对整个单元的知识进行回顾整理,结合所学的新知及旧知,完成对大单元知识的结构化。
设计单元复习课时,教师需要抓住知识的联系,通过整合练习素材,引导学生对知识结构系统地建构,使学生从整体把握单元知识结构。在本单元的复习课中,我设计了下面两道练习题。
第1 题:算一算,你发现了什么?目标是引导学生掌握小数乘法与小数除法之间的联系。
第2 题:算一算,你又发现了什么?目标是引导学生进行回顾整理,掌握除数是小数的除法、除数是整数的小数除法、整数除法三者之间的联系,有助于学生建立起“除法模块”完整的知识体系。
1.算一算,你发现了什么?
小学阶段的数学知识点相对分散,大单元教学设计对完善学生的知识体系、增强学生对知识的理解具有积极作用,实现对学生核心素养的培养和提高。
