高铁列车涂层的抗冲蚀破坏机制研究

2024-01-02曾明亮高方圆

材料保护 2023年12期

曾明亮，高方圆，刘仁，李光，夏原

(1. 中国科学院力学研究所宽域飞行工程科学与应用中心，北京 100190；2. 中国科学院大学工程科学学院，北京 100049)

0 前言

随着高速铁路的建设发展,为适应西部及北方地区的风沙环境[1,2],对高速列车在极端恶劣环境下的服役性能提出了更为苛刻的要求。目前,动车组为了美观及防腐要求在铝合金表面喷涂了聚氨酯系列涂层[3,4],运行中车体表面涂层受到空气中高速微细粒子的冲蚀会产生不同程度的磨损与破坏。对受微细粒子冲蚀的高铁列车涂层开展破坏机制与评价方法的研究,可为风沙环境下涂层结构的优化提供依据,具有重要的现实意义及工程价值。

冲蚀磨损是复杂的碰撞接触过程,属于典型的非线性问题,且影响该过程的因素有很多,各种因素之间的相互作用使得单从冲蚀试验角度难以分析其冲蚀机理。目前数值模拟技术是研究冲蚀机理的有效方法,其仿真结果作为试验研究的有效补充,能更全面地从时间和空间上获得冲蚀过程的物理信息,有利于进一步揭示冲蚀机理。针对涂层的抗冲蚀磨损研究,目前公开发表的文献多集中在通过单个粒子或多粒子对整体靶材的冲蚀来分析其冲蚀参数如粒子速度[5-7]、入射角度[8-10]及粒子粒径[11,12]等对冲蚀磨损率的影响,进而来分析材料的抗冲蚀性能。此外,现有研究为了保守计算将冲蚀粒子简化为球形[13-15],而实际过程中的粒子形状多为不规则颗粒,忽略了冲蚀粒子的形状对冲蚀磨损率的重要影响[16-20],同时关于多层涂层的冲蚀研究也较少。

ANSYS/LS-DYNA是目前国际公认的最著名的通用显式动力分析有限元软件,其对各类非线性高速碰撞、爆炸等动态冲击内容的分析十分契合。本工作通过显式动力学分析软件LS-DYNA建立高速微细粒子冲蚀模型,考虑粒子形状以及粒子分布的影响,通过模拟与试验相结合的方法,研究微细粒子在不同冲蚀参数下对涂层冲蚀磨损率的影响规律,综合分析其冲蚀磨损特性与破坏机制。

1 试验

1.1 材料及方法

本试验选用铝合金为基体,制备尺寸为25 mm×25 mm×5 mm的试样。对基体表面进行喷砂处理后,采用喷涂技术在试样表面制备了聚氨酯涂层,其结构为表层聚氨酯、中间聚酯腻子及底漆环氧树脂3层构成。微细粒子冲蚀试验采用气流喷砂式冲蚀试验机,该试验机主要由压缩空气供给系统、磨粒供给系统、测试室及除尘装置组成,其工作原理图如图1所示。

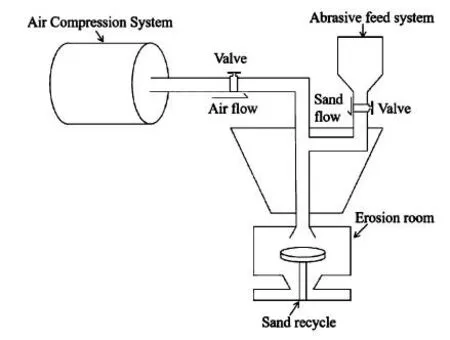
图1 喷砂式冲蚀试验机原理示意图Fig. 1 The principle diagram of erosion experiment machine

基于现有高铁列车车速在200～300 km/h范围内,普遍运行速度在250 km/h左右(约70 m/s),列车车头部位其正面迎风角为90°,固体粒子取自内蒙古中西部地区乃至北方地区沙尘天气的主要沙源之一的内蒙古鄂尔多斯高原北部的库布其沙漠[21],涂层受冲蚀粒子粒径在74～250 μm之间,平均粒径在100 μm左右。冲蚀试验前对冲蚀试验机的供料速度进行校准及测量,确定其供料速度为0.76 g/min。通过调节冲蚀试验时间控制入射粒子质量,调节喷射气流气压控制入射粒子速度,更换试样托架控制入射角度,更换筛网尺寸来控制粒径大小。采用控制变量方法研究不同冲蚀参数对冲蚀磨损率的影响,其详细冲蚀磨损试验条件见表1。

表1 冲蚀试验设计方案

为确定材料的冲蚀磨损率,首先采用 Li-3 表面轮廓测量仪测量涂层冲蚀后的冲蚀坑轮廓及粗糙度,采用 Origin 软件对冲蚀坑轮廓曲线进行积分处理,得出单位时间内试样的体积损失量,采用 FA1604 型精密天平测量冲蚀试验机供料速度,得出单位时间内冲蚀粒子的质量,定义单位质量粒子入射导致的涂层体积磨损量为涂层的冲蚀磨损率,具体计算公式如下式:

(1)

式中:Ev为涂层的冲蚀磨损率(mm3/g),ΔV为单位时间内试样的移除体积,Mp为单位时间内冲蚀颗粒质量。

1.2 有限元建模分析

实际冲蚀过程极其复杂,难以建立与其完全一致的模型,不同的粒子形状、大小、冲蚀角度、速度等都会对冲蚀结果造成较大的影响。因此结合实际的冲蚀环境,进行如下假设:

(1)考虑冲蚀粒子成分主要为SiO2,可视为刚体,形状为不规则体;

(2)忽略冲蚀粒子之间的接触与相互作用[22];

(3)忽略了涂层制备产生的空隙等内部缺陷以及残余应力。

基于上述假设,为在有限元计算中实现表层聚氨酯涂层在粒子冲蚀后的材料磨损,即单元移除,有2种方法:(1)使用自带材料失效准则的材料模型,如韧性材料Johnson-Cook 模型和脆性材料Johnson-Holmquist模型;(2)自定义材料失效准则,如使用关键字*MAT_ADD_EROSION。基于聚氨酯材料的特点,本工作采用的是第2种方法。考虑等效塑性应变累积效应,对靶体材料进行简化,其材料参数如表2所示。通过对聚氨酯涂层及石英砂颗粒形貌的观察,取涂层模型的分析面积为2 000 μm×2 000 μm,沿厚度方向依次为聚氨酯150 μm、聚酯腻子250 μm、环氧树脂200 μm,粒子模型为100 μm×100 μm×100 μm立方体切割而成的不规则体,其粒径在100 μm左右,分析单元均采用8节点缩减积分显式实体单元solid164。为确保获得的结果与实际情况更接近,粒子分布采用Matlab随机生成,涂层内部接触类型采用面面绑定接触,涂层与粒子之间的接触采用面面侵蚀接触[23],确保在表层单元移除的情况下涂层与粒子之间的接触关系仍然存在,模型全部单元为191 669个,涂层及粒子的形貌与几何模型见图2。

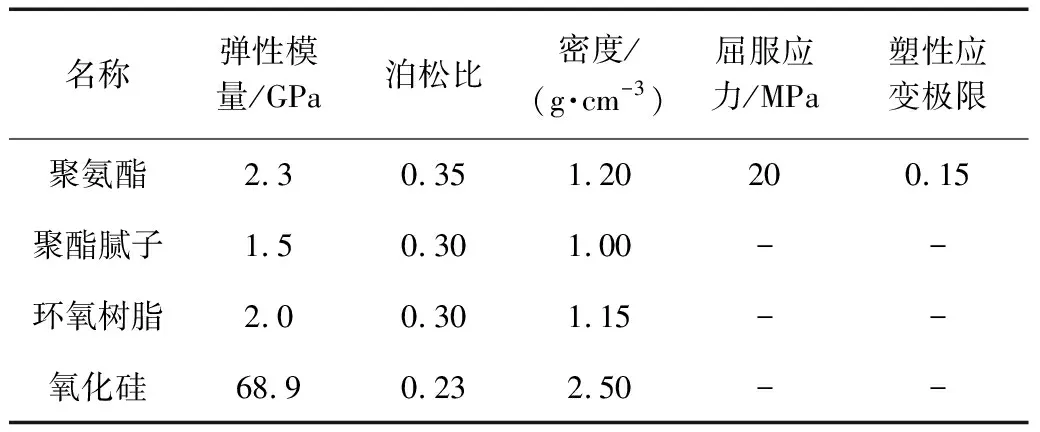
表2 材料参数

图2 涂层与粒子的形貌及几何模型Fig. 2 Morphology and finite element model of coating and particle

2 结果与分析

2.1 粒子冲蚀过程分析

模拟分析粒子粒径为100 μm,初始速度为70 m/s,入射角度为90°时的冲蚀磨损情况,考虑单个冲蚀物颗粒对靶材的冲击不足以完整准确地给出计算冲蚀率所需的数据[24],建立多固体颗粒对靶材的冲蚀有限元模型来分析材料的冲蚀磨损行为,其中共有100个入射粒子,分为10组入射,每层粒子同时冲击涂层,各组粒子冲击涂层的时间间隔为1.62 μs左右。随着入射粒子的增加,等效塑性应变逐渐累积,当涂层单元的等效塑性应变值达到材料失效的塑性应变极限时,涂层单元被移除,随着粒子冲蚀的进行移除单元数据逐渐增加,形成最终的冲蚀磨损体积,其等效塑性应变云图与演变规律如图3、图4所示。

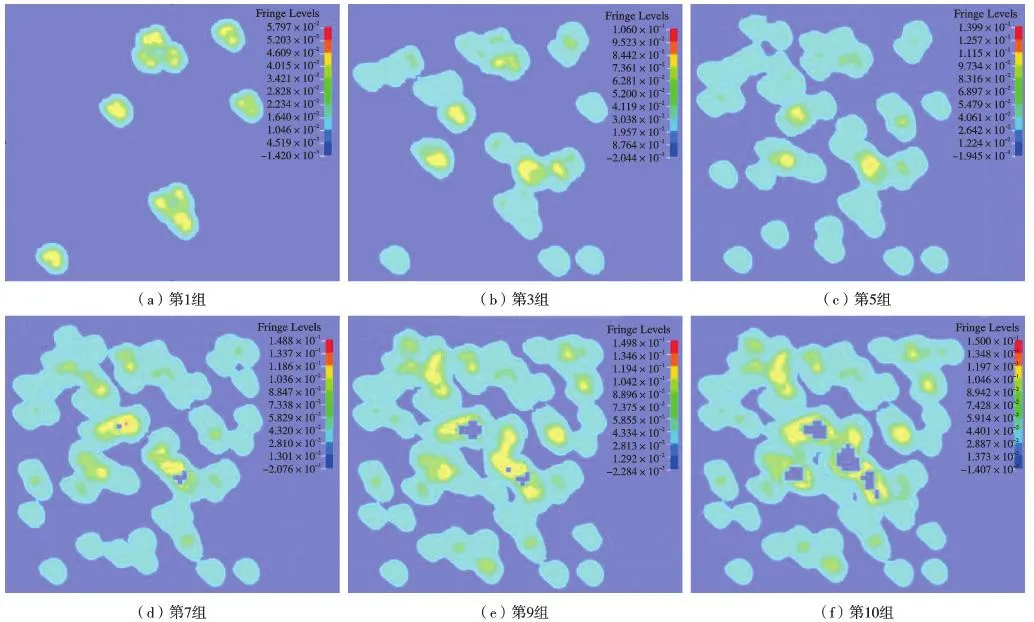
图3 聚氨酯涂层冲蚀后的等效塑性应变云图(第1,3,5,7,9,10组)Fig. 3 Equivalent plastic strain cloud of coating surface

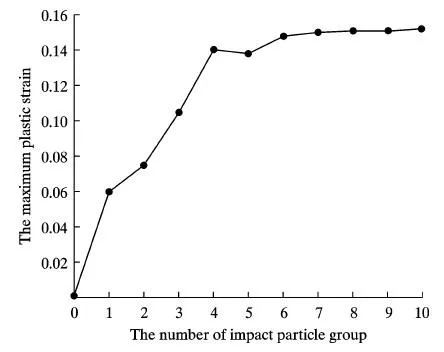
图4 涂层等效塑性应变随多组粒子冲蚀的变化曲线(第1组～第10组)Fig. 4 Variation curve of coating equivalent plastic strain with multiple particle erosion(group 1～10)

图3为聚氨酯涂层在各组粒子冲蚀后的等效塑性应变云图,可以看出,随着粒子入射,聚氨酯涂层的塑性应变最大值逐渐升高。各组粒子入射后涂层等效塑性应变最大值如图4所示, 聚氨酯单元的开始移除发生在第6组,其最大等效塑性应变与模型建立时材料参数设置塑性极限为0.15相符,统计移除单元数目,其涂层冲蚀磨损率计算结果为Ev=0.54 mm3/g;图5为聚氨酯涂层在方案1下冲蚀磨损体积随粒子质量变化曲线图,可以看出当粒子质量超过0.51 g时,其冲蚀磨损体积急剧上升。主要原因是当粒子质量超过0.51 g时聚氨酯表层已被完全冲破,露出聚酯腻子层,此后的冲蚀主要为聚酯腻子的冲蚀,而聚酯腻子的抗冲蚀能力远小于聚氨酯表层,故冲蚀磨损体积会出现急剧上升,冲蚀磨损试验测定的冲蚀磨损率为Ev=0.50 mm3/g。有限元冲蚀模拟预测值与试验测试值的误差为7%,表明该模型建立与计算方法具有较高的有效性。

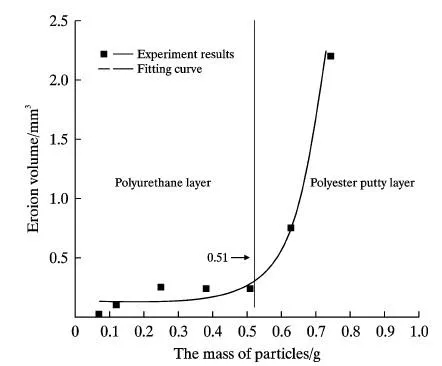
图5 冲蚀磨损体积随粒子质量的变化曲线Fig. 5 The erosion wear volume changed with the mass of impacting particles

2.2 粒子冲蚀速度的影响

冲蚀粒子速度的变化与靶材的冲蚀磨损率具有直接关系,同样在冲蚀有限元模拟计算中粒子速度的变化会直接导致涂层的应力应变响应及涂层单元的冲蚀磨损变化。粒子入射角度为90°,粒径为100 μm,粒子速度取50、60、70、80、90、100 m/s,其冲蚀模拟结果如图6所示。大量试验验证分析表明,冲蚀磨损率Ev与速度v存在如下幂函数关系:

图6 冲蚀磨损率随粒子速度的变化曲线Fig. 6 The curve of erosion rate changed with particle velocity

Ev∝vn

(2)

式中,n为速度指数。有文献表明[25],指数n的取值在2.0～2.7范围内,对不同粒子速度下的冲蚀磨损率进行乘幂拟合有:Ev=4.46×10-5·v2.27,其速度指数为2.27,与文献的报道相符合,且由上述试验方案2所进行的冲蚀试验,其拟合结果为:Ev=3.40×10-5·v2.27,得到的速度指数同样为2.27,模拟与试验结果相吻合。粒子速度小于70 m/s 时冲蚀磨损率增长缓慢,在粒子速度大于70 m/s时冲蚀磨损率增长迅速,特别地粒子速度从70 m/s 变为80 m/s 时冲蚀磨损率剧烈增长,增幅达到87%。同时通过对比不同粒子速度下冲蚀的表面形貌图(图7)可以看出,随着粒子速度的增加,涂层表面粗糙化程度逐渐增加,在粒子速度低于70 m/s 时涂层表面依然存在小块完整平面,当粒子速度增加到80 m/s时表面材料颗粒破碎程度显著增大,粒子速度达到100 m/s时涂层表面几乎无法找到完整平面,只有破碎的材料颗粒。

图7 聚氨酯涂层不同粒子速度冲蚀表面形貌Fig. 7 The surface morphology of polyurethane coating after different velocity erosion

2.3 粒子粒径的影响

为研究粒子粒径对涂层冲蚀过程的影响,图8为粒子速度为70 m/s,入射角度为90°,粒径取70、100、150、210 μm下的涂层冲蚀模拟结果。在冲蚀角度、速度一定的情况下,涂层冲蚀磨损率随着粒子粒径的增大而呈现增长趋势,且当粒子粒径增大到一定范围(粒径大于 150 μm)时涂层冲蚀磨损率逐渐趋于稳定,这与Tilly[26]和Yerramareddy等[27]的研究结果一致;且由不同粒径粒子冲蚀后的表面形貌图(图9)可以发现,粒子粒径较小时其入射造成的表面材料破碎脱落尺寸较小,而大粒径的粒子入射能导致大块破碎物脱落,表明聚氨酯涂层在不同粒径的垂直入射下均表现出脆性材料破碎脱落的冲蚀磨损机制。

图8 不同粒子粒径冲蚀模拟计算结果Fig. 8 The FEM results of different particle diameter erosion

图9 聚氨酯涂层不同粒径粒子冲蚀表面形貌Fig. 9 The surface morphology of polyurethane coating after different diameter particles erosion

2.4 粒子入射角度的影响

在冲蚀有限元模拟计算中,粒子入射角度的变化会直接导致涂层的应力应变响应,以及涂层单元的冲蚀磨损变化。图10为粒径100 μm,粒子速度70 m/s,入射角度取15°、30°、45°、60°、75°、90°下的涂层冲蚀磨损模拟结果,分析可知涂层的冲蚀磨损率在低角度入射时达到峰值,Desale等[28]指出这一最大冲蚀角是材料本身的特性,与冲蚀物的性质无关。在入射角度为 15°时涂层冲蚀磨损率达到最大值0.94 mm3/g,随着入射角度的增大,冲蚀磨损率逐渐降低最后趋于稳定,在入射角度为90°时,涂层冲蚀磨损率达到最小值0.54 mm3/g,Acierno等[29]研究不同冲击角度对热塑性聚氨酯弹性涂层的影响,给出了相同的结论。

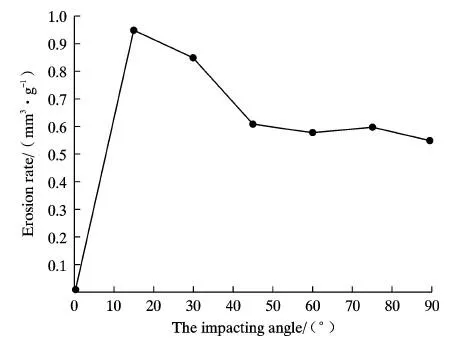
图10 不同入射角度冲蚀模拟计算结果Fig. 10 The FEM results of different impacting angle erosion

同时结合不同粒子入射角度时的冲蚀形貌图(图11)可以看出,粒子入射角度为15°时,由于粒子硬度远高于涂层硬度,粒子入射在涂层表面造成划擦与切削带走材料,使得涂层微切削形成冲蚀坑从而产生冲蚀磨损;入射角度为90°时,粒子入射造成聚氨酯表面材料变形,变形达到临界值时产生微细裂纹,随着粒子的持续入射裂纹交错扩展导致表面材料破碎脱落,从而形成冲蚀磨损。综合分析可得聚氨酯涂层在粒子低角度冲蚀情形下表现出韧性材料微切削冲蚀磨损机制,在粒子高角度冲蚀情形下表现出脆性材料破碎脱落冲蚀磨损机制。

图11 聚氨酯涂层不同角度下的冲蚀表面形貌Fig. 11 Surface morphology of polyurethane coating with different angles of erosion

3 讨论

基于以上的数值模拟与试验结果,可以得到聚氨酯涂层随着粒子入射角度的不同表现出不同的冲蚀磨损机制,下面就不同冲蚀磨损模式下的材料损失进行分析,其对材料的抗磨损设计有着重要意义。

对于韧性材料,在固体粒子冲击作用下的材料损失是由冲击粒子对靶材的切削、成屑作用以及累积的塑性变形造成的,或是循环载荷下的疲劳磨损效应。靶材受粒子冲击时,冲击粒子的动能转化为靶材的变形能和切削能。当韧性材料受粒子法向冲击时,其冲击能量主要转化为靶材的内能,韧性靶材随之发生较为明显的塑性变形,而材料的损失相对较小。在斜角冲击时,多数韧性材料的磨屑是其冲击时的过大剪切力造成的,属于剪切失效行为,材料表现出最大的冲蚀率;脆性材料在冲蚀粒子冲击作用下几乎不发生塑性变形,在冲蚀粒子的反复冲击下,应力超过材料强度,固体粒子与靶材表面进行能量交换,动能转化为材料形变并引起材料表面或内部裂纹的萌生、扩展和交结而导致材料的脱落,从而造成材料损失,而材料的破坏与粒子初始动能的法向分量有关[25],因此脆性材料在垂直冲击下表现出最大冲蚀率,模拟与试验结果也与之对应。

综上,分别从韧性和脆性角度深入讨论了材料的冲蚀磨损机制,在绝大多数情况下低冲蚀角下脆性材料耐冲蚀,高冲蚀角下韧性材料耐冲蚀。因此就高速列车的涂层设计而言,在考虑提升涂层的力学性能的同时,也应合理安排列车车体表面不同位置处的涂层配置。

目前关于聚氨酯涂层的耐冲蚀研究多是集中在单一因素对冲蚀磨损率的影响,而聚氨酯涂层的冲蚀磨损过程是受多种因素的耦合作用,对于冲蚀参数之间的关联性与聚氨酯涂层自身性能的相关性研究较少,后续研究将集中在以下方面:

(1)从机理到现象:反应到材料属性上体现为材料的硬度、弹性模量、屈服应力/应变、摩擦系数等均会影响其耐冲蚀性能,在保证材料硬度的前提下,提高其断裂韧性是增强其抗冲蚀的能力的有效手段,对于弹性体材料,在较低硬度值下通常表现出更好的抗冲蚀性[30];

(2)从宏观到微观:涂层的结晶度、基本组成成分及比例、分子量、交联度以及填料等因素是影响粒子冲蚀性能的关键参数[31-33],通过对材料进行改性的手段,改变其微观结构,可达到增强、增韧的目的;

(3)从单一磨损机制到多种磨损机制交互作用:冲蚀磨损的材料损失机制随材料的不同而有所不同,复合材料的冲蚀磨损并非单纯由某一种磨损机制作用,多数情况下是由多种磨损机制交互作用,但可能由某一种冲蚀理论起主导作用,冲蚀磨损的数值仿真分析可为复合材料的多样化的磨损交互作用作进一步的理论补充。