基于改进遗传算法的沥青路面再生工厂布局优化

肖子豪,郭小宏

(重庆交通大学经济与管理学院,重庆 400074)

在沥青路面再生工厂规划建设过程中,车间布局是一个重要却又复杂的部分。不仅各功能单元的相互关系、物料搬运距离会对布局规划产生影响,而且各功能单元的布置方式也会对布局产生制约。仅使用传统的方法,比如分支定界法[1]、割平面法[2]和系统布局规划法[3](system layout planning, SLP),解决多个功能单元的布局规划问题时效率很低[4],只能完成规模较小的布置组合内容。车间布局优化在降低车间物料搬运成本及提高生产效率方面起到了重要的作用[5]。近年来,智能算法作为主要研究手段被广泛应用于车间布局优化的研究中。周润博[6]、谢晖[7]利用遗传算法结合SLP法,以物流成本最小和功能区相关性最大为目标对公司生产车间进行布局优化,有效缩短了物料搬运距离,提高了企业的生产效率。张广泰等[8]融合熵权-逼近理想解排序法,基于遗传算法对SLP法进行了改进,提高了车间布局的非物流关系强度。赵欢[9]采用剩余矩形排样算法和遗传算法,考虑设备布局与总体布局的耦合得到二次优化布局,减少了厂区总体布局费用。卢义桢等[10]引入自适应遗传算子策略,提出改进的遗传模拟退火算法求解模型,有效降低了物流成本和缩短了搬运时间。董舒豪等[11]采用遗传模拟退火算法,针对多行设施布局优化模型,进行分段编码并以实例验证了其优越性。伍义[12]、李孟雪[13]、杨雅楠[14]采用遗传算法及遗传模拟退火算法,以非物流相关性最大、物流成本最小、碳排放最少为目标得到了布局优化方案。但是,目前针对再生工厂车间布局优化问题所采用的遗传算法仍存在一些不足:1)再生工厂的各个功能单元并非成行布置,其放置位置受到车间边界、功能单元间距约束的影响。现有算法采用间接编码方式,各功能单元的布置位置信息表达不直观,编码解码复杂度高,影响了算法的效率;2)现有遗传算法针对初始种群的设定方法并不明确,对于种群的优化方法欠佳使得算法的全局搜索能力不强,易陷入局部最优。

基于此,笔者采用实数分层编码,分为坐标层和放置方式层,分别对应各车间的坐标及放置状态,使信息表达更加直观,降低编码难度,减少求解时间;并针对初始布局进行排列组合得到初始种群,提高设定效率,增加其多样性。坐标层采用多点变异,放置方式层采用单点变异,引入模拟退火算子,增加了繁殖更优个体的概率,提高了算法的局部搜索性能。

1 工厂布局相关概念和数学模型

1.1 功能单元划分与联系

沥青路面再生工厂的工艺流程为将回收的RAP料进行破碎筛分,得到不同粒径的基准料,烘干后按一定的比例与新集料、粉料、沥青和再生剂进行混合搅拌,最终得到再生成品料。按加工对象,对生产设备进行分类组合实现功能单元的划分,如表1所示,再根据工艺关系梳理各功能单元之间的联系,如图1所示。

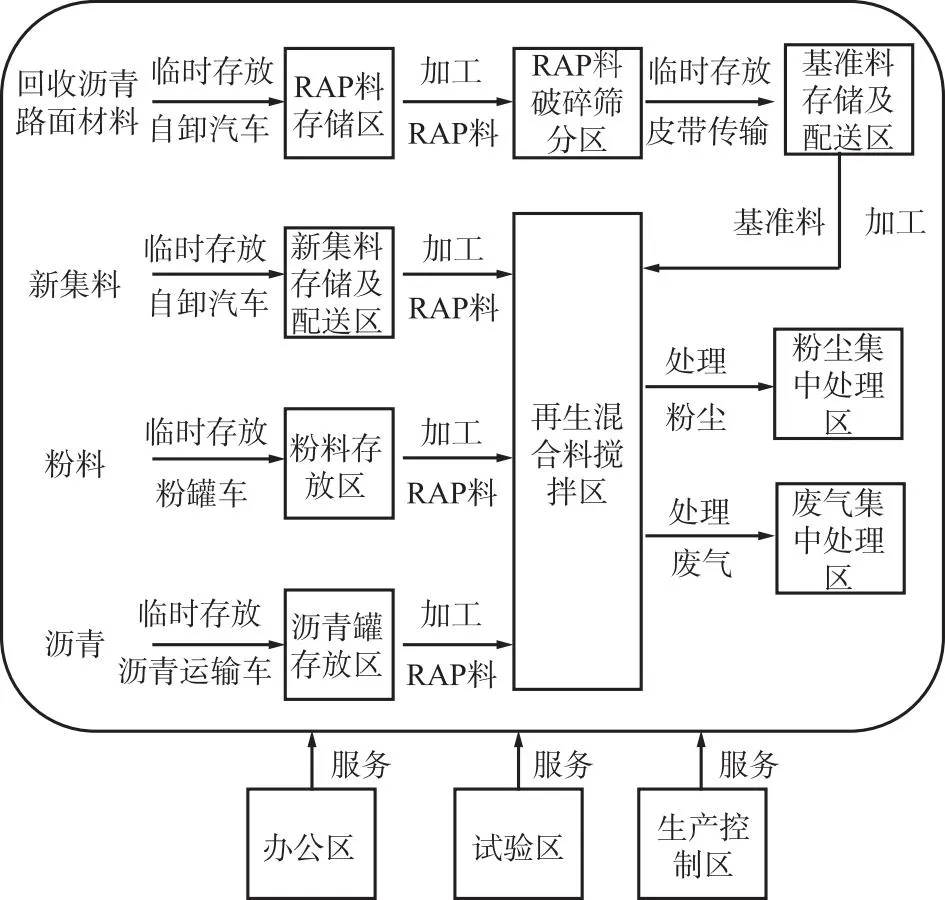
图1 功能单元联系图Fig.1 Contact diagram of functional unit

表1 沥青路面再生工厂的功能单元划分

1.2 功能单元位置信息表示

再生工厂车间布局是指按照一定约束,在给定的布局范围内对各个功能单元进行合理布置,从而达成多目标的协调。需布局的车间范围在一个长为L,宽为W的矩形内部,车间左下角为坐标原点。各功能单元的形状假定为矩形,均平行于X轴或Y轴放置,功能单元之间保持一定的活动距离,其位置信息指矩形中心的横、纵坐标,放置方式是指其平行于X轴或Y轴放置,表示为

(x1,x2,…,xj,…,xn-1,xn),

(1)

(y1,y2,…,yj,…,yn-1,yn),

(2)

(z1,z2,…,zj,…,zn-1,zn)。

(3)

式(1)—式(3)中:xn表示第n个功能单元的横坐标;yn表示第n个功能单元的纵坐标;zn表示第n个功能单元的放置方式;xj,yj,zj分别表示第j个功能单元的横坐标、纵坐标、放置方式。

车间和功能单元的布局模型如图2所示,其中:Fi,Fj,Fk为功能单元代号;lj为某功能单元的长度;wj为某功能单元的宽度;sx,sy为功能单元在X轴、Y轴方向上与车间边界的活动间距;sxf,syf为2个功能单元之间在X轴、Y轴方向上的安全间距;L为车间长度;W为车间宽度。

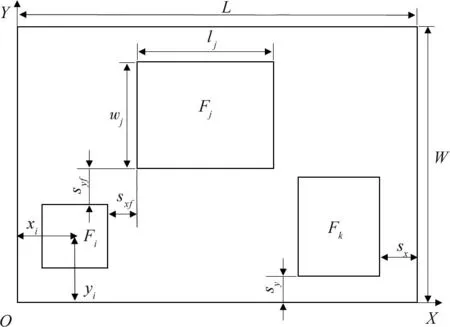
图2 车间和功能单元布局模型图Fig.2 Layout model of workshop and functional units

1.3 方向约束

当功能单元的长边平行于X轴时,将其视为横向放置;当功能单元的长边平行于Y轴时,将其视为竖向放置。

(4)

功能单元的放置方式如图3所示。

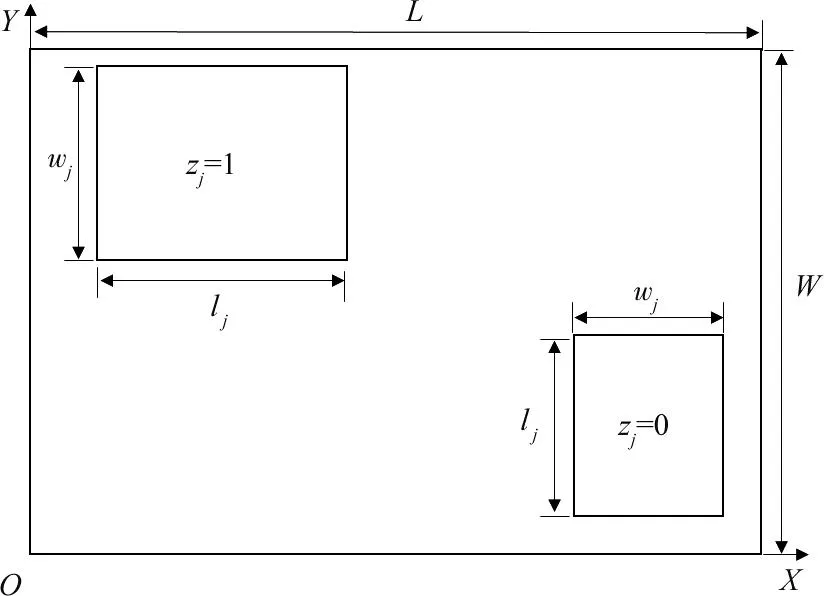
图3 功能单元的放置方式示例Fig.3 Example of how functional units are placed

1.4 边界约束

功能单元的布置位置应落在车间范围内,且与车间边界保持一定的间距。

(5)

1.5 间距约束

车间内部的任意功能单元之间互不重合,在X轴或Y轴方向上至少保留大小为sxf或syf的间距,且每个功能单元只能被布置1次。

Ujk×Vjk=0,

(6)

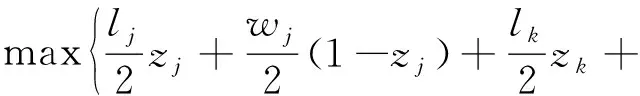
(7)

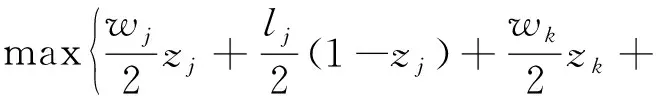
(8)

式(6)—式(8)中:Ujk表示判断j功能单元和k功能单元在X轴方向上是否重叠;Vjk表示判断j功能单元和k功能单元在Y轴方向上是否重叠。

1.6 目标函数

车间布局优化以非物流关系强度最大、物流成本最小及碳排放最少为目标,其具体计算方式参考文献[15],目标函数设定如下:

(9)

式中:D表示目标函数值;a1表示非物流关系强度权重;D1表示非物流关系强度值;D1max表示非物流关系强度最大值;a2表示物料搬运成本权重;D2表示物流成本值;D2max表示物料搬运成本最大值;a3表示碳排放权重;D3表示碳排放值;D3max表示碳排放最大值。

2 改进遗传算法

2.1 实数分层编码

遗传算法的编码和解码方法很大程度上决定了算法的可行性和效率,因此设计适宜的编码和解码方法极为重要。针对再生工厂车间布局问题,采用传统的二进制编码会使种群个体过于冗长,且不同位置的个体在十进制编码转换为二进制编码时长度可能不一致,导致编码过于复杂。为解决传统遗传算法在布置位置和放置方式表示问题上的不足,提出实数分层编码方法,在降低编码难度的同时,能够直观表示各功能单元的布置位置和放置方式。用分层编码的方式映射3个决策层(横坐标层、纵坐标层以及放置方式层)共同对目标函数产生的影响。

图4所示为实数分层编码示例。第1层为横坐标层,实数表示功能单元在车间布局范围内的横坐标;第2层为纵坐标层,实数表示功能单元在车间布局范围内的纵坐标;第3层为放置方式层,反映各功能单元的放置方式:数字1表示该功能单元横向放置,数字0表示竖向放置。

图4 实数分层编码示例Fig.4 Example of real number layered coding

实数分层编码的解码方式相对简便,只需将横坐标层、纵坐标层以及放置方式层中的数字按编码顺序列出。图4所示的再生工厂车间布局方案解码输出结果如表2所示。

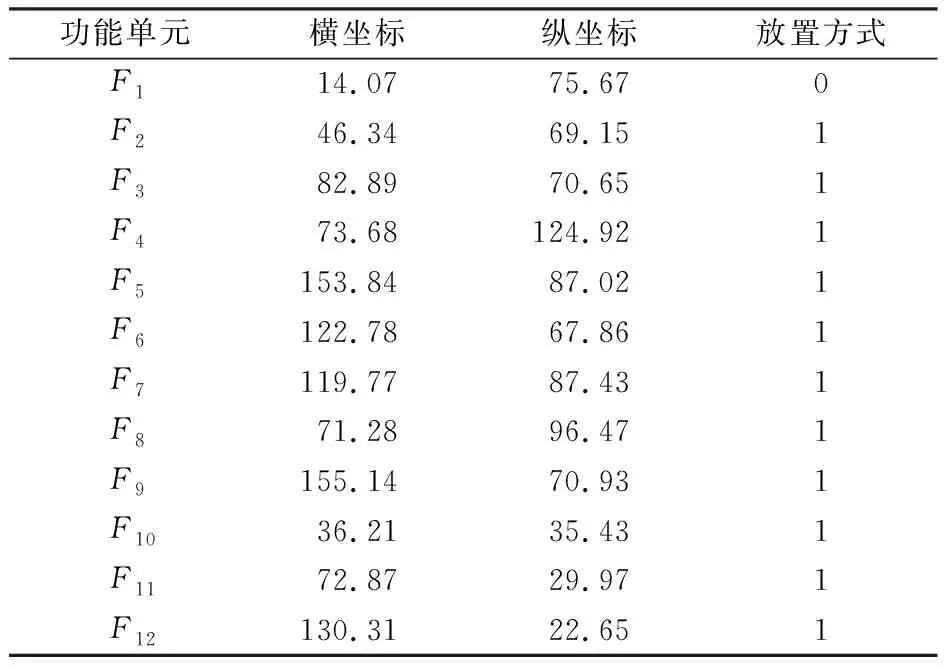
表2 布局方案解码输出结果

2.2 初始种群设定

由于再生工厂车间布局的范围偏大、功能单元数量偏多,采用车间边界内随机生成功能单元布置位置的方法效率低下。提出基于初始方案的排列组合方法,将初始方案作为初始种群之一,其余种群个体采用各功能单元横、纵坐标和放置方式交换的方法得到。由于生成1～12的全排列数组数量超出MATLAB软件行数范围,遂生成1～6和7～12的2个全排列数组,对其进行排列组合并将顺序与初始布局方案相同的数组剔除,从而得到1～12的排列数组。将初始方案按该数组排列放置,通过判断得到的方案是否符合约束条件,并计算符合约束条件方案的目标函数值,从中筛选出剩余的种群个体,保证初始种群个体的有效性,增加初始种群个体的多样性。

2.3 交叉算子

交叉算子是产生新个体的主要方式,在算法中起核心作用,决定了算法的性能优劣。在交叉操作中,染色体的前2行作为交换的基本单元,即横坐标层和纵坐标层进行算术交叉,放置方式层不进行交叉,这能够保证子代与父代的放置方式一致。编码交叉操作示例如图5所示,图中α=0.2,具体步骤如下。

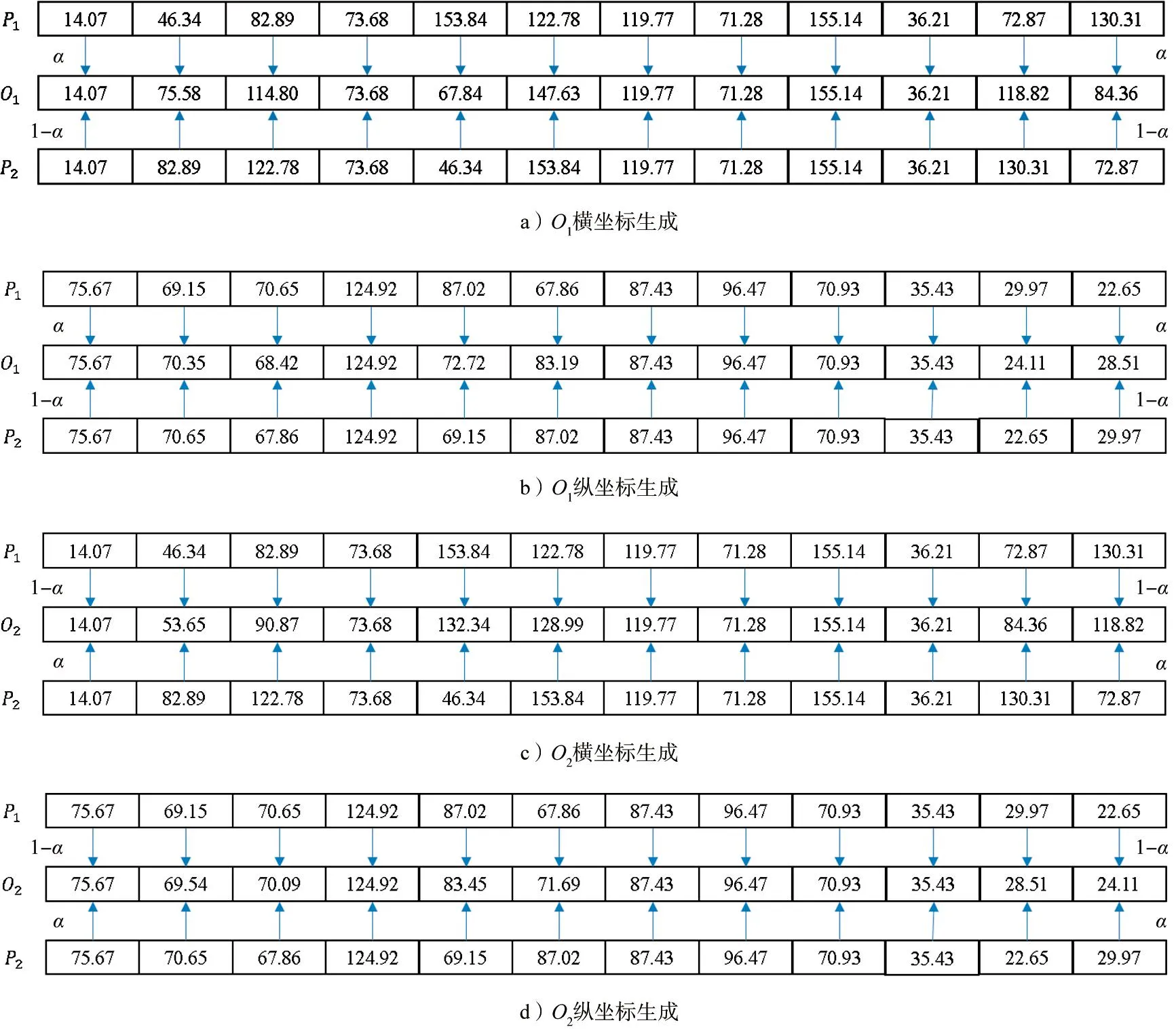
图5 编码交叉操作示例图Fig.5 Example diagram of coding cross operation

步骤1 从种群中选择相邻的2条染色体,提取其横坐标层和纵坐标层作为父代基因P1和P2。

步骤2 将父代基因P1和P2进行算术交叉,生成2个子代基因O1和O2。算术表达式为

O1=α×P1+(1-α)×P2,

(10)

O2=(1-α)×P1+α×P2,

(11)

式中:α表示(-0.5,1.5)内的随机数。

步骤3 将生成的子代基因O1和O2分别与父代染色体P1和P2的放置方式层基因结合,得到2个新的种群个体。

2.4 变异算子

变异算子任意改变所选染色体的一个或多个基因,以增加种群的结构可变性,能防止算法过早收敛。针对坐标层,引入模拟退火算子,在迭代初期,于全局范围内搜索最优值。随着迭代次数的增加,搜索范围逐渐减小,便于寻找近似最优解的精确解,提高算法的搜索效率。对于放置方式层,采用单点变异的方式。

1)横坐标层、纵坐标层的变异

示例如图6所示,具体步骤如下。

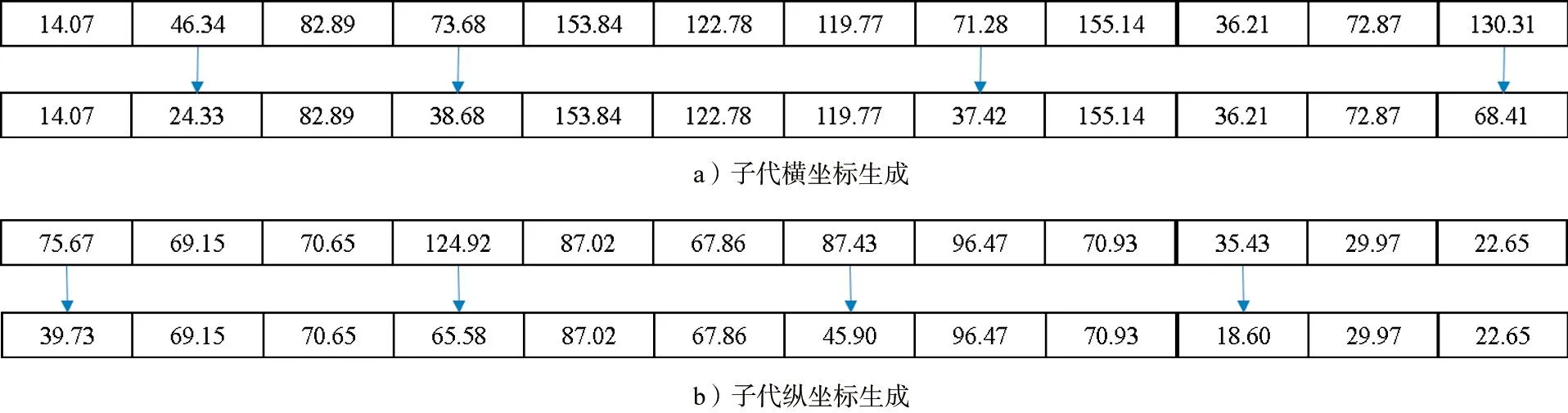
图6 横坐标层和纵坐标层变异示例图Fig.6 Example diagram of horizontal and vertical coordinate layer variation

步骤1 生成2个(0,1)范围内的1×12随机数列矩阵,找出数值小于变异概率的位置下标并标记。

步骤2 对横坐标层和纵坐标层标记位置的数据进行变异,变异公式如下:

a=a+a×b×0.95gen,

(12)

式中:a表示横坐标层和纵坐标层标记位置的数据;b表示(-1,1)内的一个随机数;gen表示迭代次数。图中b取-0.5,gen取1。

步骤3 将变异后的数据作为基因对应标记位置放回染色体内。

2)放置方式层的变异

放置方式层采用单点变异,示例如图7所示,具体步骤如下。

图7 放置方式层变异示例图Fig.7 Example diagram of placement method layer variation

步骤1 生成[1,12]范围内的一个随机整数,找出该整数对应放置方式层的位置下标并标记。

步骤2 对放置方式层标记位置的数据进行变异,变异公式如下:

(13)

式中:c表示放置方式层标记位置的数据。

步骤3 将变异后的数据作为基因对应标记位置放回染色体内。

将变异后的横坐标层、纵坐标层和放置方式层基因组合,得到新的种群个体。

2.5 改进遗传算法实现步骤

传统的车间布局遗传算法编码复杂,增加了解码的难度和时间,布局位置和放置方式信息表达不够直观,且搜索算子设置单一,导致算法的寻优能力不足。本文针对传统遗传算法进行改进,提出实数分层编码方法,引入模拟退火算子,清晰表达功能单元的布局位置和放置方式信息,增强算法寻求最优解的能力,具体步骤如下。

步骤1 根据再生工厂车间布局的约束,基于初始布局方案得到满足约束条件的初始种群个体。

步骤2 计算种群个体的适应度函数值,采用轮盘赌方法进行种群个体的选择。

步骤3 依次选择相邻的2个种群个体,将其横坐标层、纵坐标层作为父代基因进行交叉,之后与父代的放置方式层基因结合,得到新的种群个体。

步骤4 根据变异概率,对种群个体依次进行横坐标层、纵坐标层和放置方式层变异,得到新的种群个体。

步骤5 计算新种群中个体的目标函数值,对目标函数值进行排序。保留部分优秀个体,并将其与父代染色体中优秀的个体结合,形成新的种群。

步骤6 判断迭代次数是否满足算法终止条件。是则输出计算结果,否则返回步骤2。

3 实例验证

为验证改进算法的有效性,以某沥青路面再生工厂为研究对象。该再生工厂车间的长L=180 m,宽W=150 m,生产大门位于(0,118),各功能单元均位于布局范围内,且与车间边界的间距sx,sy均大于或等于5 m。各功能单元尺寸、布局位置与车间边界的间距如表3所示,初始布局方案如图8所示。

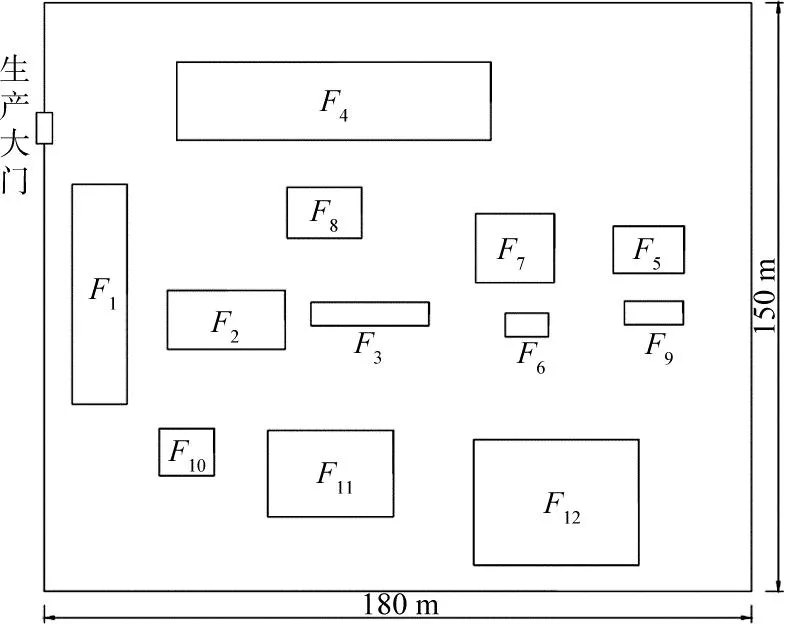
图8 初始布局方案图Fig.8 Plan of initial layout

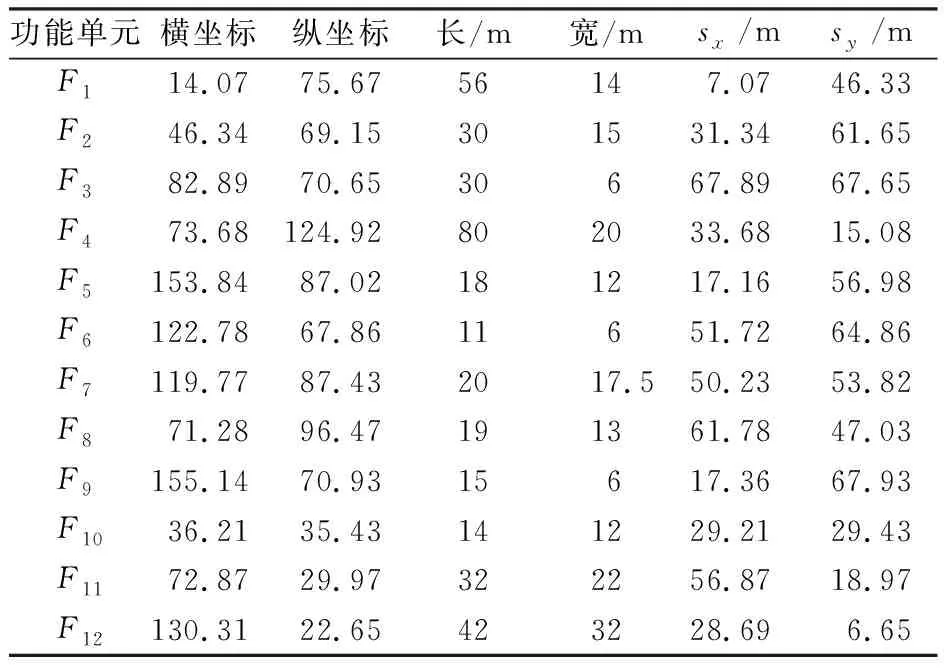
表3 功能单元信息

利用MATLAB 2016a完成改进遗传算法的编写。设置初始种群规模大小NIND=200、变异概率Pm=0.2、最大迭代次数MAXGEN=200。通过算法进行求解,得到如下结果:优化后的目标函数值为0.423 3,优化后的布局位置和放置方式如表4所示。

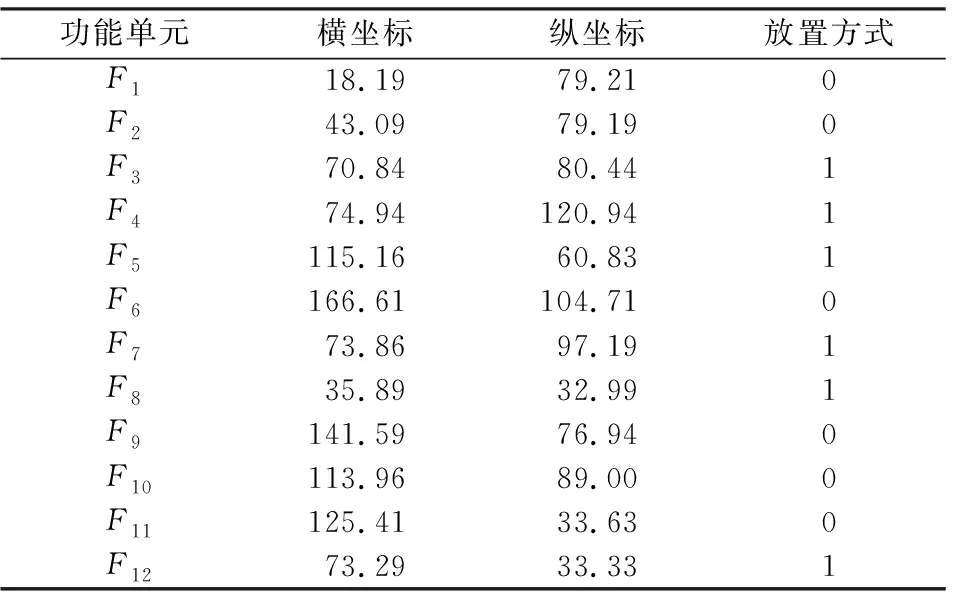
表4 优化后功能单元布局位置和放置方式表

将原始布局方案与优化布局方案数据依照优化目标计算,得到相应结果,其对比如表5所示。

表5 方案优化前后效果对比

根据表5对比结果可知,优化后的布局方案中各功能单元的非物流关系强度提高7.96,每日物料搬运成本减少14 468.85元,每日碳排放减少30.59 kg。

为验证文中算法的有效性,将传统遗传算法、文献[14]中的遗传算法应用于该实例并进行比较,迭代过程如图9所示,3种算法得到的目标函数值与迭代次数的对比如表6所示。

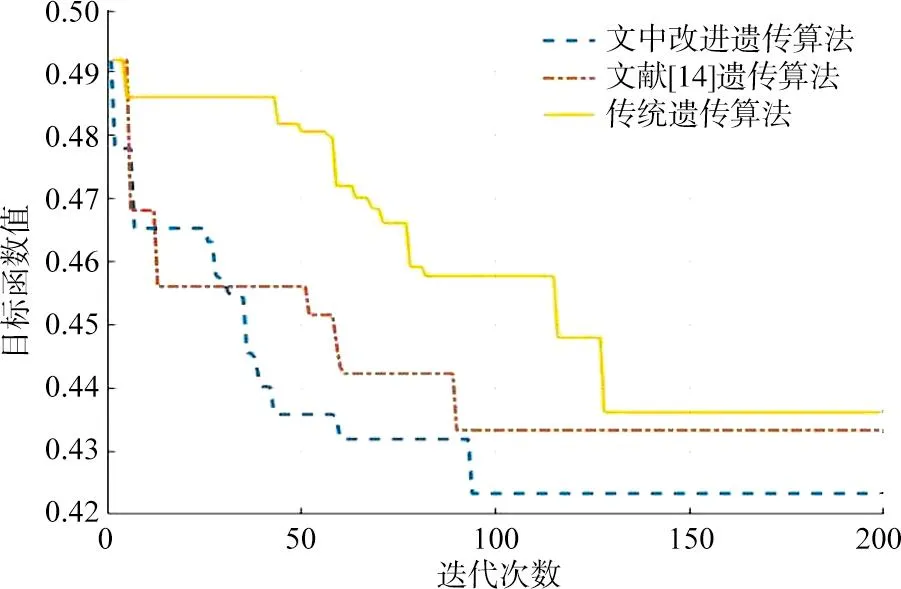
图9 算法迭代过程Fig.9 Process of algorithm iteration

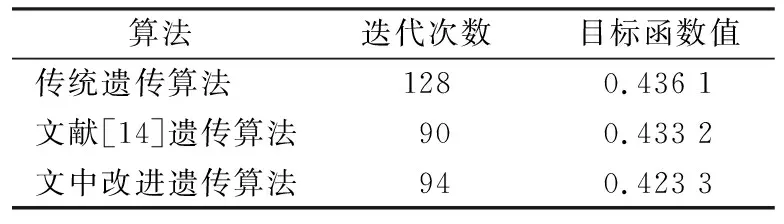
表6 迭代结果对比

从表6对比3种算法迭代结果可知,改进后的遗传算法较传统遗传算法迭代次数减少34次,目标函数值减少0.012 8,较文献[14]中遗传算法迭代次数相近,目标函数值减少0.009 9。

4 结 语

笔者针对沥青路面再生工厂布局优化,采用遗传算法对其初始种群设定方式、编码方式与交叉和变异方式进行明确及改进,得到如下结论。

1)采用实数分层编码,以功能单元布局位置的横、纵坐标和放置方式代替传统的二进制编码,增强了布局位置信息表示的直观性,降低了解码复杂度,减少了算法求解时间,提高了运行效率。

2)基于初始布局方案,采用排列组合得到初始种群,增加了初始种群的多样性。

3)针对算法的变异引入模拟退火算子,使得寻优能力提升,从而可以高效地对布局方案进行优化。

4)实例表明,改进后的遗传算法较传统遗传算法迭代次数减少34次,目标函数值减少0.012 8,较文献[14]中目标函数值减少0.009 9。优化后的布局方案中,每日物料搬运成本减少14 468.85元,碳排放减少30.59 kg。改进后的方法可为沥青路面再生工厂布局优化提供参考与技术支持。

本文利用MATLAB仅生成了1～12全排列的部分数组,未生成全部数组,今后可完善全部数组以丰富初始种群,增加其多样性,并利用约束条件筛选出更为优秀的种群个体,从而提高算法的寻优能力。此外,本文的研究仅引入模拟退火算子,后续可引入其他算子,并针对再生工厂布局优化算法进行改进。