基于持续到达信号强度的辐射源定位方法

2024-01-02张游杰郑伟伟陈学丽张清萍马俊明暴一忱

河北工业科技 2023年6期

张游杰,郑伟伟,吴伟,陈学丽,张清萍,马俊明,暴一忱

(1.中国电子科技集团公司第三十三研究所,山西太原 030032;2.华南理工大学计算机科学与工程学院,广东广州 510641)

辐射源定位是获取电磁信号源位置信息的重要技术手段。分布式无源定位利用分散的多个传感器接收电磁辐射源信号进行定位[1],具有覆盖范围大、隐藏性好、容错性高、网络构建灵活方便等优点,在军事、民用等诸多领域得到广泛应用[1-2]。已知的分布式无源定位方法有基于到达角(angle of arrival,AOA)[3]、基于到达时间(time of arrival,TOA)[4]、基于到达信号强度(strength of arrival,SOA)[5]、基于到达时间差(time difference of arrival,TDOA)[6-7]、基于到达频率差(frequency difference of arrival,FDOA)[7]的定位方法,以及基于TDOA和AOA、基于FDOA和AOA、基于TDOA和FDOA的联合定位方法等[8-9]。

这些方法各有优缺点。其中,AOA是利用信号的角度特征值完成定位,但对误差比较敏感;TOA和TDOA是利用信号传播时间这一特征值完成定位,定位稳定,但要求各基站间有严格的时钟同步,费用较高[1-9];SOA定位方法利用电磁波在空间中传输的距离与损耗的关系,通过同步测量多个观测点特定频率的信号强度,可推算出辐射源的位置信息[5],但是,SOA定位方法对各个监测点的时钟同步要求同样较高,各测点时钟的误差将造成定位误差增大或定位失败。为此,根据SOA定位方法的原理,提出一种基于持续到达信号强度(continuous strength of arrival,CSOA)的定位方法,简称为CSOA定位方法。该方法可通过持续测量多个观测点特定频率的信号强度,有效降低对时钟同步的要求。

1 辐射源定位问题

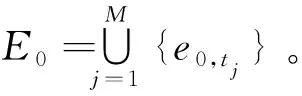
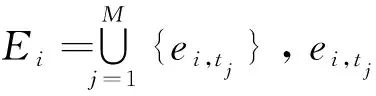
1)各个观测点不在同一个平面或同一条直线上[10];

2)每个观测点与辐射源间无遮挡;

3)各个观测点可连续测量频率为F的电磁波信号强度;

4)n≥5。

在此条件下,通过持续观测各个观测点位置信息及所接收的信号强度值,利用CSOA定位方法,可推算出辐射源O的空间坐标为(x0,y0,h0)。

2 CSOA定位方法

由于辐射源到观测点无遮挡物,且电磁波频率低于10 GHz时在空气中传播的损耗可忽略不计[11],故可认为电磁波从辐射源O到观测点Gi之间的损耗Los等于电磁波在自由空间中传输的损耗。在不考虑电磁波在空间传输所耗时间的情况下,其公式为

Los=e0,tj-ei,tj=32.44+20lgF+20lgDi,

(1)

式(1)中:Los为电磁波在自由空间中传输的损耗,dB;F为频率,MHz;Di为观测点Gi到辐射源O的直线距离(i=1,2,…,n;j=1,2,…,M),km,

(2)

由式(1)转换,并在等式两边同乘以tj可得:

ei,tjtj=e0,tjtj-tj(32.44+20lgF+20lgDi)。

(3)

将M个时刻的数据相加,可得:

(4)

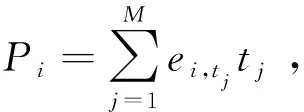
则Pi=Q-20TlgDi,变换可得:

lgDi=(Q-Pi)/(20T),

Di2=10(Q-Pi)/(10T)=10Q/(10T)/10Pi/(10T)。

令B=10Q/(10T),K=10Pi/(10T),则Di2=B/K,KDi2=B。将式(2)代入,可得:

K[(xi-xr0)2+(yi-yr0)2+(hi-hr0)2]=B,

(5)

式(5)变换得:

2K(xixr0+yiyr0+hihr0)-K(xr02+yr02+hr02)+B=K(xi2+yi2+hi2)。

(6)

令Y=K(xi2+yi2+hi2),X0=2Kxi,X1=2Kyi,X2=2Khi,X3=-K,a0=xr0,a1=yr0,a2=hr0,a3=xr02+yr02+hr02,a4=B,代入式(6),可得:

a0X0+a1X1+a2X2+a3X3+a4=Y。

(7)

式(7)是一个线性表达式,用该式对(X0,X1,X2,X3,Y) 的观测值(X0i,X1i,X2i,X3i,Yi)(i=0,1,…,n-1)进行多元线性回归分析,可计算得出回归系数a0,a1,a2,a3,a4。其中, (X0i,X1i,X2i,X3i,Yi)(i=0,1,…,n-1)可由Gi的n组观测值 (xi,yi,hi,Ei)计算得出。

由此最后可推算出结果:

x0=a0,y0=a1,h0=a2。

3 实现方法

CSOA定位方法的关键算法是多元线性回归。可利用文献[12]给出的基于最小二乘法实现的多元线性回归方法。

为了判定计算结果的有效性,CSOA方法利用了复相关系数r来判断线性回归效果,并定义了位置偏差系数c和信号强度方差d2个变量来衡量结果的准确性[12-17]。

位置偏差系数:

由式(7)的条件可知,c越接近于0说明计算结果的准确性越高。

信号强度方差:

(8)

式(8)中,Pi,Q,Di,T的计算公式见式(5),但要将其中的xr0,yr0,hr0用x0,y0,h0代替。由式(5)的条件可知,d越接近于0说明计算结果的准确性越高。

当r接近于1,c和d接近于0时,表示定位结果值有效,可认为定位成功。其取值具体范围在不同的场景下可根据经验值设定,例如本文所采用的仿真环境下的取值范围可设定为r>0.8,且c<4,且d<49。

4 仿真实验

为验证CSOA方法的正确性及适应性,对其进行仿真分析。为方便比对,实验采用与文献[14]相同的软硬件环境,以及相同的仿真环境。实验软硬件环境:Windows 7(64 bit旗舰版),8 GB运行内存,Intel®CoreTMi7-6700 CPU @ 3.40 GHz;开发环境为Visual Studio 2013,C#语言;仿真环境:假定一个仿真空间,长、宽、高分别为100,100,20 m,该空间中的西南方向最下方的顶点坐标作为原点(0,0,0);在该空间中,辐射源位于(10,10,10)处,持续向外辐射频率为30 MHz的电磁波信号,信号强度随机变化。

4.1 仿真实验方法

4.1.1 信号源仿真

通过一个长度为5 000万的循环队列仿真信号源,记为ET0。队列中相邻元素表示相邻时刻的信号强度,元素的值为区间(-40,0)内的随机实数,单位为dBm。对该仿真信号源做如下假定:

1)在下一个时刻之前信号源的辐射强度不变;

2)队列中连续2个元素之间的时间差为100 μs,即信号源的辐射强度每100 μs发生1次变化。

4.1.2 观测点仿真

观测点的仿真方法如下。

1)假定一个开始测量时刻,记为tick,对应循环队列ET0的某个位置。所有观测点在此时刻同时开始测量。

2)假定观测点通过频谱扫描的方式测量数据,经过连续M次扫描后得到一组测量值。每次扫描所用的时间称为驻留时间,记为sweeptime;每次扫描之间存在一定时间间隔,在这个时间间隔内,不对信号强度进行测量,称为丢弃时间,记为droptime。驻留时间与丢弃时间分别对应ET0的一个子集,且两者对应的子集相邻。

3)驻留时间对应ET0的子集,由多个元素组成。每次扫描的测量值由该子集的多个元素仿真计算而成。测量值的仿真计算方法:①将每个元素通过式(1)计算得到当前观测点对应的值,单位为dBm;②将单位由dBm转换为Vpp;③计算完成所有元素到当前观测点的对应值后,以Vpp为单位统计其平均值;④将平均值的单位转换为dBm,即为本次扫描的仿真测量值。此过程中,dBm与Vpp按阻抗为50 Ω进行相互转换,其公式为

{dBm}=10+20lg(0.5 {Vpp}),

(9)

(10)

4)理想情况下每个观测点的开始时刻、驻留时间完全相同,丢弃时间为0。但实际测量中每个观测点的开始时刻、驻留时间可能会存在一定随机误差,丢弃时间也是一个大于0的随机数据。开始时刻的误差只在第1次扫描时产生,在其后的扫描中该值不变;驻留时间的误差与丢弃时间在每次扫描时都有可能改变。这些误差统称为观测时间误差,都可以采用随机数的方式仿真。

5)在仿真模拟计算观测点测量值时,应考虑到观测点位置和测量值的误差,同样可采用随机数的方式仿真。

4.2 仿真实验步骤

仿真实验的步骤如下。

第1步构建仿真信号源的循环队列。

第2步在仿真空间内,随机生成n(n≥5)个观测点,并设定开始时刻tick、持续测量次数M、每次扫描的驻留时间sweeptime,以及各个参数的误差范围。

第3步按照给定的条件生成每个观测点的模拟测量值序列。其方法如下。

由式(1)可知观测点Gi在任意时刻的信号强度为

ei=e0-32.44-20lgF-20lgD,

(11)

式中e0是该时刻辐射源的强度。由式(11)可计算出ET0中的任一元素对应观测点Gi监测到的信号强度,在此基础上增加测量值的随机误差、观测点位置的随机误差,即可用于计算仿真数据。其公式为

ei=e0-32.44-20lgF-20lgD′+NE·rand(-0.5,0.5),

(12)

式(12)中:NE是观测点测量时所产生随机误差的幅值;函数rand(-0.5,0.5)可产生位于区间(-0.5,0.5)的随机数;D′是增加位置随机误差后,观测点到辐射源的距离,并且

式中:xN,yN,hN分别是观测点位置增加随机误差后在x,y,z轴方向的坐标。可表示为

xN=x+Nx·rand(-0.5,0.5),

yN=y+Ny·rand(-0.5,0.5),

hN=h+Nh·rand(-0.5,0.5),

式中:Nx,Ny,Nh分别是观测点在x,y,z轴方向随机误差的幅值。

在驻留时间对应ET0的子集中,具有多个元素,将会产生多个ei。按照观测点仿真中观测值的计算方法,可得到第j次扫描的观测值ei,tj。在计算过程中,所用的元素集合应是考虑到观测时间误差后的ET0的子集。

在M次扫描完成后,可利用式(4)—式(7)形成观测值序列,其中tj的值为sweeptime。

设M=1 000,sweeptime=1 000 μs时,随机分布的10个观测点的仿真数据如表1所示。

表1 10个观测点的模拟数据

第4步利用模拟生成的观测点位置及观测值序列,通过CSOA方法,推算出辐射源O的位置。如果推算成功,则与给定的辐射源位置比较,计算其距离。

最后,给定不同的仿真条件,将第2步到第4步重复多次,分析各参数对定位精度的影响。

4.3 仿真分析

通过多项仿真实验验证观测点的测点数、位置误差、测量误差、观测时间误差及扫描次数对定位成功率和定位精度的影响。

每项仿真实验均设定不同条件,重复至少10 000次“4.2”项所述的仿真实验步骤,每次推算的结果记为(x0,y0,h0) ,然后计算与辐射源O真实位置的距离,即定位误差,记为s。

最后,通过累积分布函数,比较不同参数下定位误差s的分布,总结各项参数对定位结果的影响。

4.3.1 测点数对结果的影响及有效性判定

为了解测点数n对定位结果的影响,通过11组实验进行测试,测点数n的取值范围设为5～15。按照普通的频谱分析仪配合普通计算机能达到的性能指标,其他参数的取值:驻留时间sweeptime设为10 ms,开始时刻误差的幅值tickerr设为1 s,驻留时间误差的幅值sweeptimeerr设为1 ms,丢弃时间误差的幅值droperr设为1 ms,测量误差的幅值Ne设为0.2 dBm,观测点位置随机误差的幅值Nx,Ny,Nh均设为0.4 m,扫描次数M设为1 000。每组实验重复50 000次,在不考虑有效性判定(只要通过前文所述的多元线性回归得出结果即认为定位成功)时,其定位成功率见表2。

基于该条件,计算定位误差的累积分布,如图1所示。

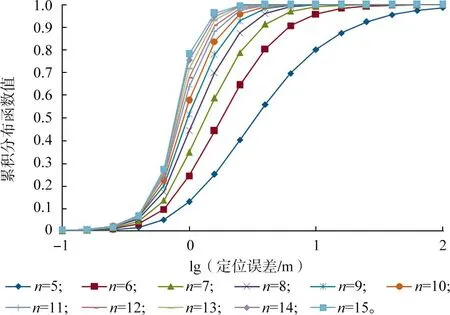
图1 测点数对定位精度的影响(不判定有效性)Fig.1 Impact of measurement points on location accuracy (without determining the validity)

由图1可知,随着n的增加,累积分布函数在较低的定位误差时趋于1,定位误差越来越集中在较低的数值,定位精度越来越高。但是,随着n的增大,提升的幅度越来越小。以定位误差在100.6m(约3.98 m)处的累积分布函数值为例:n=5时,累积分布函数值为0.559,n=6时,累积分布函数值为0.805,累积分布增幅达44.0%;n=10时,累积分布函数值为0.993,n=11时,累积分布函数值为0.997,累积分布增幅仅为0.4%。与文献[5]及文献[13]的实验结果进行比对,可发现,CSOA方法与SOA方法一样:n≤10时,增加测点数可显著提高定位精度;n>10以后,增加测点数可继续提高定位精度,但效果明显变缓;n>15以后,增加测点数对定位精度的影响将变得很小。

为实现有效性判定,对复相关系数r、位置偏差系数c和信号强度方差d进行验证。图2为r,c和d的统计图,其中r是n=6时的最小值统计图(因为实验中n=5时所有的r=1),c和d为n=5时的均值统计图。由图中可看到,定位误差为102m(100 m)以内时,r的值不会小于0.8;定位误差在100.8m(约6.31 m)处时,c的值明显增大,超过了4;定位误差在101.8m(约63.10 m)处时,d的值急剧增大,超过了48。

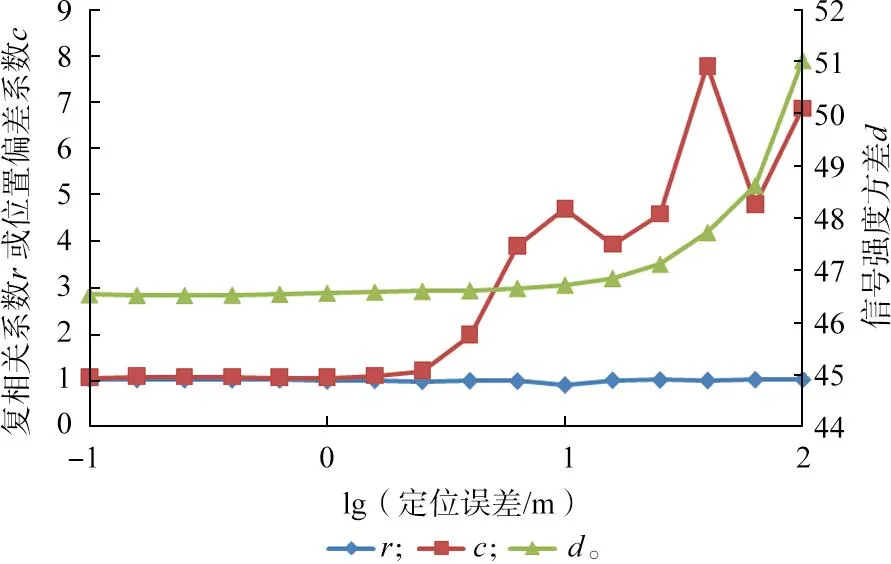
图2 有效性判定参数统计图Fig.2 Statistical chart of validity determination parameters

基于此结果,增加有效性判定,然后对本次实验的数据重新统计,结果见表3和图3。基于图2和实验中总结的一些经验数据,本文仿真环境下的有效性判定条件为r>0.8,且c<4,且d<49。

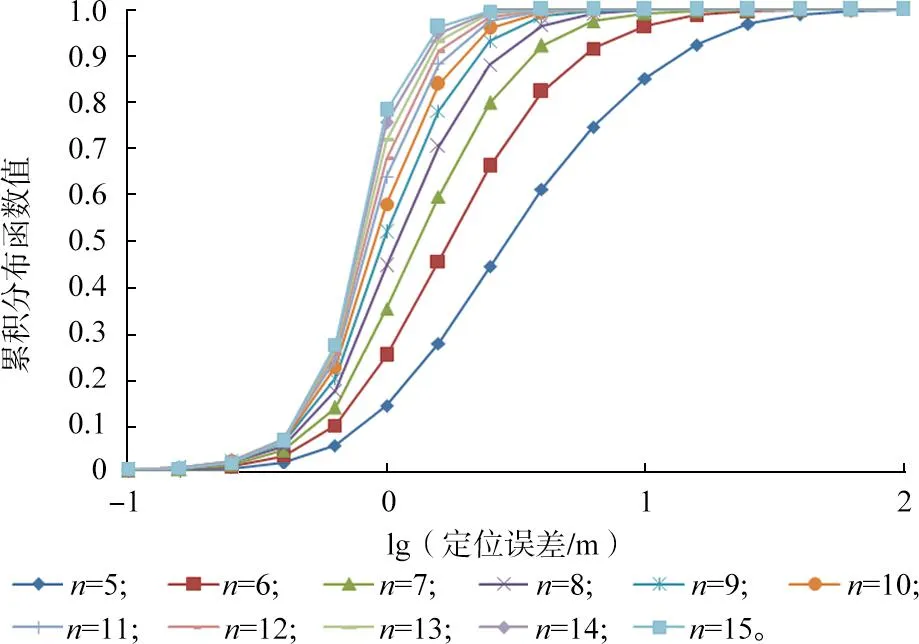
图3 测点数对定位精度的影响(判定有效性)Fig.3 Impact of measurement points on location accuracy (determining the validity)

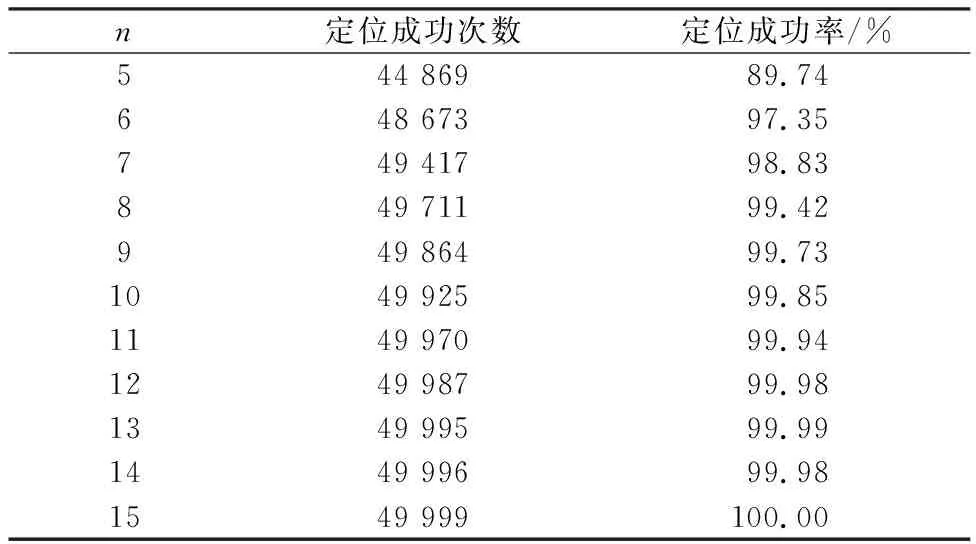
表3 有效性判定后的测点数与定位成功率

与不考虑有效性判定的情况比较,可发现定位成功率下降了,但定位精度得到了提升。以n=5为例,定位成功率由98.94%下降到89.74%,下降9.2个百分点;在定位误差为100.6m(约3.98 m)处的累积分布函数值,由图1中的0.559提高到图3中的0.610,提高9.12%。证明有效性判定可在一定程度上剔除定位不准确的结果。

根据本次实验的结果,在下面的实验中,测点数全部设为5,结果全部经过有效性判定,判定条件与本实验相同。

4.3.2 观测点位置误差对结果的影响

为了解观测点位置误差对定位结果的影响,通过6组实验进行测试,每组位置误差的幅值Nxyh(Nx,Ny,Nh全部设为Nxyh)分别为0.2,0.4,0.6,1.2,1.6,2.0 m。其他参数设置为n=5,sweeptime=10 ms, ticker=1 s,sweeptimeerr=1 ms, droperr=1 ms,Ne=0.2 dBm,M=1 000。

每组实验重复100 000次,经有效性判定后,其定位成功率见表4。

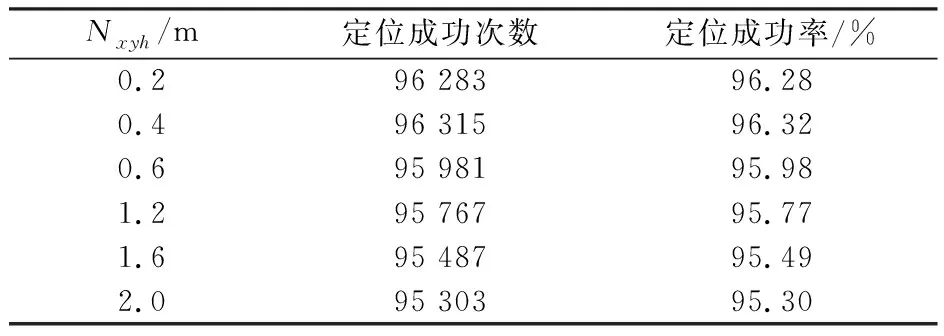
表4 观测点位置误差与定位成功率

基于该条件,计算定位误差的累积分布函数值,结果如图4所示。

图4 位置误差对定位精度的影响Fig.4 Influence of position error on location accuracy

由表4可知,位置误差的增大,会使定位成功率下降;位置误差幅值小于等于0.4时,定位误差于100.4m(约2.51 m)处趋于一致;位置误差幅值小于等于1.2时,定位误差于100.6m(约3.98 m)处趋于一致;位置误差幅值小于等于2.0时,定位误差于100.8m(约6.31 m)处趋于一致。由此可知,位置误差在一定范围内对定位精度影响较大,超过该范围则影响较小。

4.3.3 测量误差对结果的影响

为了解观测点测量误差对定位结果的影响,通过6组实验进行测试,每组观测点测量误差的幅值Ne分别为0.2,0.4,0.6,0.8,1.0,1.2 dBm。其他参数设置为n=5,sweeptime=10 ms,ticker=1 s,sweeptimeerr=1 ms,droperr=1 ms,Nx=Ny=Nh=0.4 m,M=1 000。

每组实验重复100 000次,经有效性判定后,其定位成功率见表5。

表5 测量误差与定位成功率

基于该条件,计算定位误差的累积分布函数值,结果如图5所示。

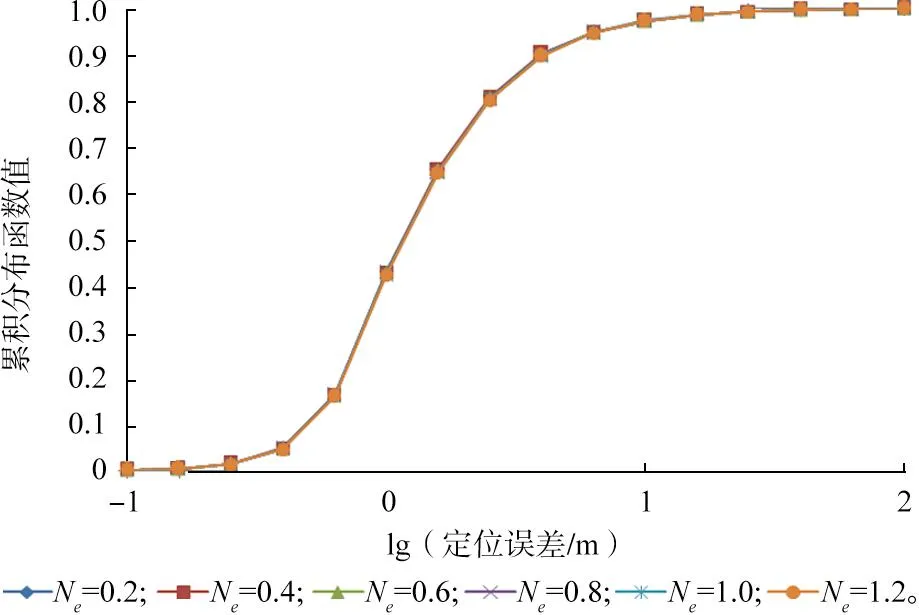
图5 测量误差对定位精度的影响Fig.5 Influence of measurement error on location accuracy

由表5和图5可知,测量误差的大小与定位成功率没有明显的关系,同时测量误差对定位精度的影响也基本可以忽略。分析其原因:测量的过程实际上是一个信号强度按时间积分的过程,在积分过程中,测量产生的随机误差会互相抵消,最终降低了对定位精度的影响。

4.3.4 观测时间误差对结果的影响

观测时间误差即为开始时刻误差。在一般的实际应用中,各观测点的开始时刻误差较大,而驻留时间误差与丢弃时间较小。因此,为了解观测时间误差对定位结果的影响,实验中将sweeptimeerr与droperr固定,只改变sweeptime与tickerr。实验分为14组:前7组sweeptime=10 ms,tickerr分别为10,20,50,100,200,500,1 000 ms(1 s);后7组sweeptime=100 ms, tickerr分别为100 ms,200 ms,500 ms,1 s,2 s,5 s,10 s。其他参数设置:n=5, sweeptimeerr=1 ms,droperr=1 ms,Ne=0.2 dBm,Nx=Ny=Nh=0.4 m,M=1 000。

每组实验重复10 000次,经有效性判定后,其定位成功率见表6。其中rate为误差时间占比,即开始时刻误差在持续扫描总时长中的比例,rate=100[tickerr/(sweeptime·M)],%。

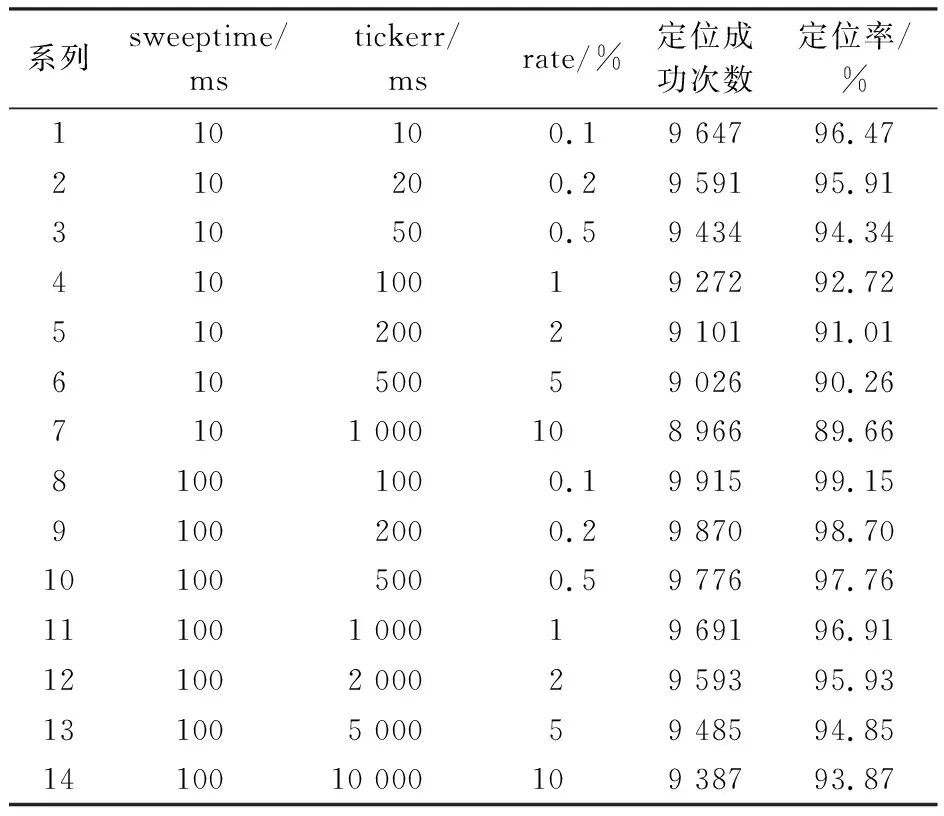
表6 开始时刻误差与定位成功率

基于该条件,计算定位误差的累积分布函数值,结果如图6所示。

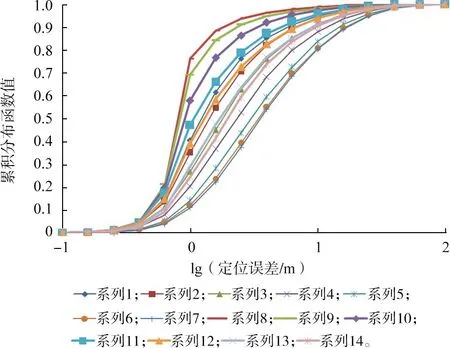
图6 开始时刻误差对定位精度的影响Fig.6 Effect of starting time error on location accuracy

通过比较表6和图6中的系列1—系列7或系列8—系列14,可以发现:开始时刻误差对定位成功率与定位精度的影响较大。在其他参数不变的情况下,误差时间占比越大,定位成功率越小,定位精度也越低。以系列1与系列7为例,定位成功率由96.47%下降到89.66%,下降6.81个百分点;在定位误差100.6m(约3.98 m)处,累积分布函数值由0.852下降到0.541,下降36.5%。

而在同样误差时间占比的情况下,单次扫描的驻留时间sweeptime越大,定位成功率越高,定位精度也越高。如系列1,误差时间占比为0.1%,但其定位成功率介于系列11(误差时间占比为1%)与系列12(误差时间占比为2%)之间,其定位精度曲线与系列12的曲线几乎重叠。误差时间占比同为0.1%的系列8与之相比,定位成功率从96.47%提高到99.15%,提高了2.68个百分点,在定位误差100.6m(约3.98 m)处,累积分布函数值由0.852提高到0.962,提高了12.9%。分析其原因:观测时间误差中除开始时刻误差外,驻留时间误差及丢弃时间也会对结果造成影响;增大驻留时间,可使后两者在驻留时间中的占比变小,所造成的影响也会变小,从而可提高定位成功率与定位精度。

由此可见,CSOA方法可以有效解决时钟不同步带来的误差问题。

4.3.5 扫描次数对结果的影响

为了解扫描次数对定位结果的影响,通过7组实验进行测试,每组扫描次数M分别为1 000,2 000,5 000,10 000,20 000,50 000,100 000。其他参数设置为n=5, sweeptime=10 ms, ticker=1 s,sweeptimeerr=1 ms,droperr=1 ms,Ne=0.2 dBm,Nx=Ny=Nh=0.4 m。

每组实验重复10 000次,经有效性判定后,其定位成功率见表7。

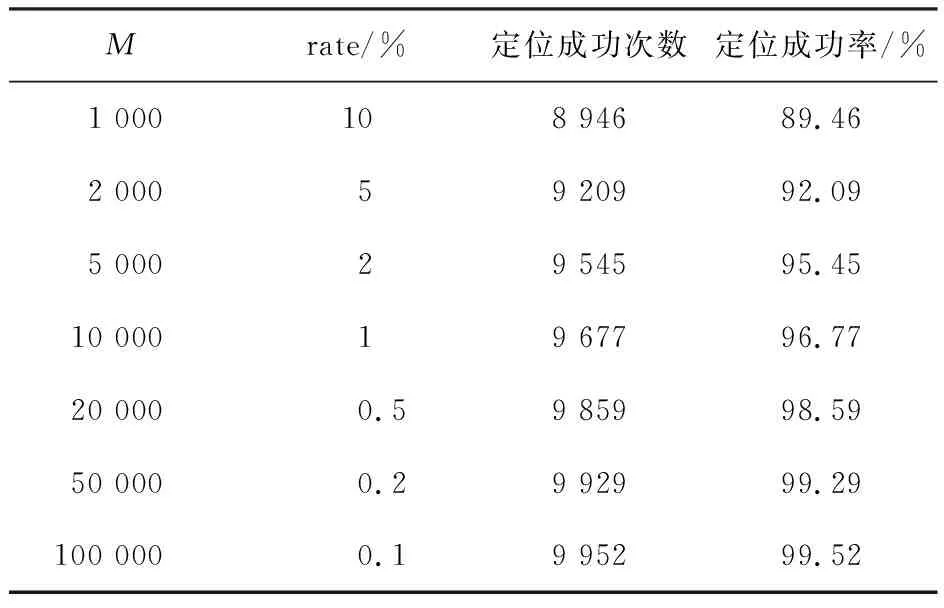
表7 扫描次数与定位成功率

基于该条件,计算定位误差的累积分布函数值,结果如图7所示。

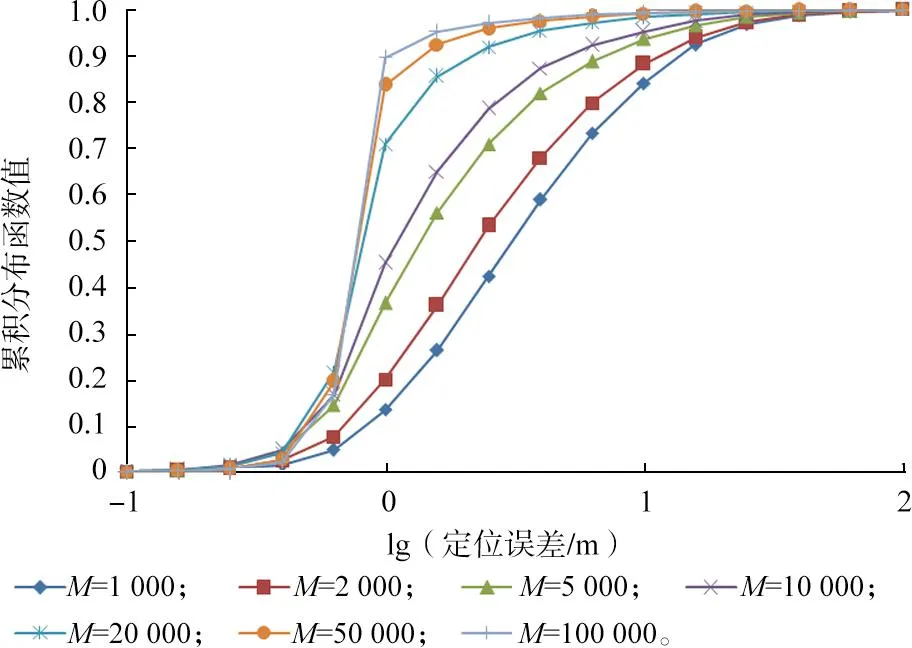
图7 扫描次数对定位精度的影响Fig.7 Influence of scanning times on location accuracy

由表7和图7可知,随着扫描次数M的增加,定位成功率和定位精度得到了明显的提升。当M从1 000提高到100 000时,定位成功率由89.46提高到99.52,提高了10.06个百分点;定位误差在100.6m(约3.98 m)处的累积分布函数值,由0.590提高到0.985,提高66.9%。可见增加扫描次数,可以大幅度提高定位成功率与定位精度。

4.3.6 CSOA方法与SOA方法的比较

本实验用于比较CSOA方法与SOA方法在定位成功率与定位精度方面的差别。对CSOA方法,按照“4.3.1”项所述的参数设置,SOA方法则采用与本次仿真实验相同的测量误差及观测点误差。

每组实验重复50 000次,在不考虑有效性判定时,其定位成功率如表8所示。

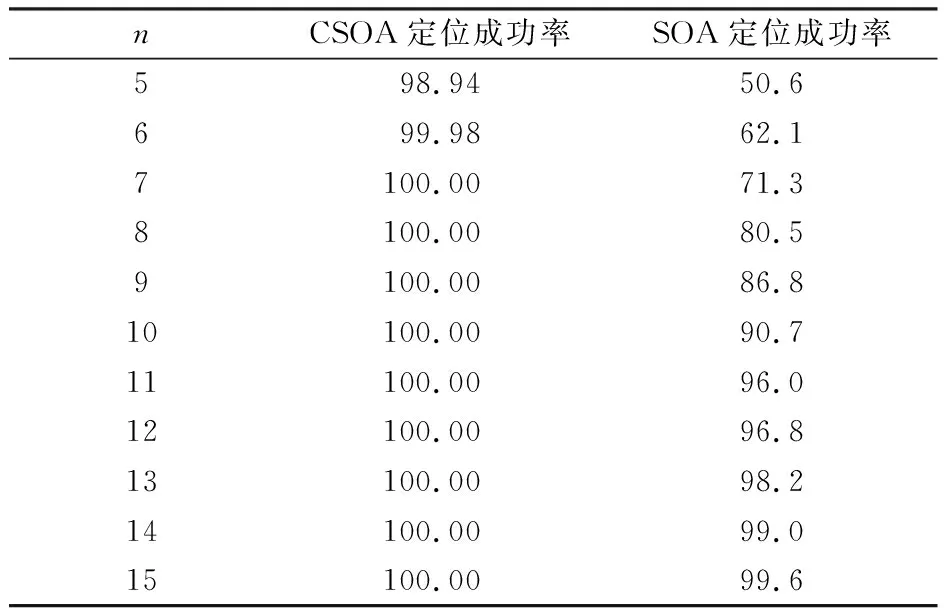
表8 不考虑有效性判定的CSOA与SOA定位成功率比对

基于该条件,计算SOA定位误差的累积分布函数值,结果如图8所示。

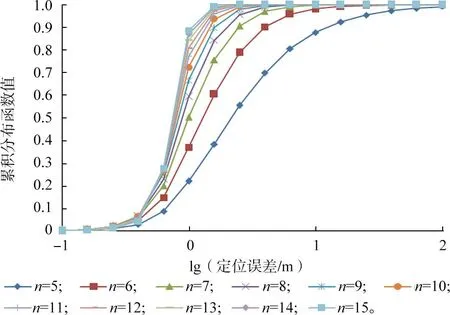
图8 SOA方法测点数对定位精度的影响Fig.8 Influence of SOA method measurement points on location accuracy

由表8可知,相同的条件下,CSOA方法在测点数为5时,其定位成功率高于SOA方法测点数为13时的效果。对比图8和图1,以定位误差在100.6m(约3.98 m)处的累积分布函数值为例进行比较:CSOA方法在n=5时的值为0.559;而SOA方法在n=5时值为0.366,n=6时累积分布函数值为0.557。可见CSOA方法可以采用较少的测点数达到较好的效果。