基于自抗扰的无人机舵系统大惯量柔性颤振抑制*

张 强，苏伟杰，王厚浩，林秀沪，杨启源

（上海航天控制技术研究所，上海 201109）

引 言

无人机舵系统作为无人机的关键组成部分，主要用来控制无人机的左右副翼、方向舵和升降舵的偏转，从而实现无人机的飞行姿态控制。国外Volz公司、Futaba公司、Parker宇航、霍尼韦尔、Micropilot等国际知名企业均在无人机电动舵机领域积累了丰富的经验，形成了系列化小功率电动舵机的研制生产能力。国内北京航空航天大学、西北工业大学、哈尔滨工业大学、上海航天控制技术研究所等单位也开展了无人机用电动舵机的研究，但在产品化方面仍与国外存在一定的差距[1]。

某型国产化大型商业无人机由现有成熟飞机运5改制而成，由于未改变飞机原有的机械结构，因此舵面惯量较大，同时舵机与舵面之间的机械传动为具有柔性的多级连杆机构。大惯量和柔性在特定情况下会引起颤振，颤振频率点限制了无人机舵系统的带宽上限，并且颤振对无人机舵系统有极大的破坏性。轻微的颤振会增加多级连杆的疲劳损伤，缩短舵系统的使用寿命；严重的颤振会导致多级连杆断裂，影响舵系统的安全可靠运行。因此，为了提高无人机舵系统的可用带宽上限并保证系统的安全运行，消除运行过程中可能存在的颤振尤为重要。

针对系统运行过程中可能存在的颤振问题，大量文献给出了理论分析和研究。文献[2]通过计算流体动力学（Computational Fluid Dynamics, CFD）数值模拟分析某战术导弹舵面高频抖动机理。文献[3]以典型飞行器的空气舵系统为研究对象，对活动部件之间的间隙、摩擦等非线性因素以及结构弹性效应开展舵系统非线性动力学建模、灵敏度分析、气动弹性分析等研究。文献[4]依据试验数据构建了舵机伺服系统及舵面结构有限元模型，并进行了整个系统的固有频率计算；结合固有频率计算结果，利用偶极子网格空气动力模型进行舵面及操纵系统颤振计算。文献[5]提出了在舵机电流环加入超前滞后环节的颤振抑制措施。文献[6]针对某高超声速舵面颤振风洞试验模型开展了数值模拟研究，采用多种气动力模型和耦合迭代策略研究颤振预测。本文通过数学建模和仿真对无人机舵系统大惯量柔性颤振问题进行了理论分析和仿真验证，提出采用自抗扰来主动抑制颤振的方法，并通过仿真验证检验了方法的有效性。

1 数学建模与分析

该型无人机舵机与舵面之间的机械传动为具有柔性的多级连杆机构，并且舵面惯量较大，因此不能简单地将系统作为一个单独刚体进行建模。将舵系统全部惯量折算成舵机侧惯量和舵面侧惯量，这样就可得到典型的双惯量系统传动模型，如图1所示。

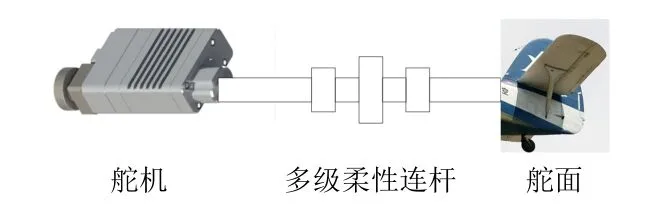
图1 舵系统双惯量系统传动模型

多级连杆传动机构是柔性的，当舵机产生的驱动力作用在连杆上时，会使连杆发生形变并产生相应的连杆力矩，连杆力矩和负载力矩共同作用在舵面惯量上，使舵面获得预期的偏转。在实际的舵系统中，传动都是金属结构，几乎没有机械阻尼，对控制的影响非常微弱。为了简化分析，采用忽略阻尼的双惯量舵系统运动微分方程组：

式中：Jm和Jd分别为舵机惯量和舵面惯量；Te，Ts和Tl分别为电机力矩、舵机力矩和负载力矩；Ks为多级连杆柔性系数；θm和θd分别为电机转动角度和舵面偏转角度；ωm和ωd分别为电机转动速度和舵面偏转速度。

对式（1）方程组进行拉普拉斯变换可以得到拉普拉斯方程组（s表示拉普拉斯算子）：

由式（2）可以推得舵面位置和电机力矩之间的传递函数G(s)：

由式（3）可知，系统传递函数由一个二阶纯惯性环节和一个二阶振荡环节组成。二阶纯惯性环节等效于舵系统中不存在柔性：双积分器乘以总惯量；二阶振荡环节则体现了柔性耦合的作用。舵面的自然颤振频率ωNTF为：

2 自抗扰控制器设计

舵系统颤振问题通常可以从结构和控制两方面来解决。最常见的颤振来源于柔性连接器，显然可以采用刚性连接器来消除或减弱柔性环节，从而消除或减轻颤振；也可以通过增加阻尼或增加舵机舵面惯量比的方式来抑制颤振[7]。然而，这些结构一旦确定，再更改并反复调试的成本非常高。不少研究人员尝试从控制方面来解决问题，采用陷波[8]和双二阶等滤波器补偿来降低颤振频率下的增益，从而抑制颤振。也有人使用复杂的自适应滤波等复杂的现代控制方法来解决。然而，采用补偿方法需要精度非常高的数学模型，即使付出很大代价获得模型，在颤振频率下也可能发生变化，使得滤波器补偿方法的效果不是非常理想，并且复杂的现代控制方法实现起来也非常复杂。

本文采用自抗扰方法来解决舵系统的颤振问题。自抗扰控制可以对扰动进行实时估计与消减，只需要很少的数学模型就能够使舵系统在较大范围内抵抗未知动态变化，并且实现起来非常简单[9]。采用这种方法时，颤振对于运动的影响可被实时估计和消除，从而使得舵系统在一定程度上类似于刚体[10]。

自抗扰控制基本框架如图2所示。其核心思想是以串联积分器为标准型，将系统动态中不同于标准型的部分视为总扰动（包括内扰和外扰），以扩张状态观测器为手段，实时对总扰动进行估计并消除，从而将充满扰动和不确定性的被控对象还原为标准的积分器串联型。

图2 自抗扰控制基本框架

2.1 控制策略设计

将式（3）传递函数重写为：

式中，d代表模型不确定性以及外部扰动。

将式（5）中等号右边的部分写为：

作为估计的总扰动。只要观测器的带宽足够，就能够将总扰动消除。

重新列写系统模型为：

采用如下控制律T′e：

式中：ˆf为观测器观测得到的总扰动；Te0为经过控制后输出的电机力矩。这样就能将式（7）变为串联积分器对象，即系统标准型。

2.2 扩张状态观测器及控制律设计

系统模型状态定义为：

系统状态空间描述为：

设计隆伯格形式的扩张状态观测器为[11]：

式（11）整理可得：

观测器的特征多项式为[12]：

式中，I为五阶单位矩阵。

式（13）整理可得：

为更好地估计系统状态和总扰动，需选取合适的l1···l5使观测器快速收敛。一般能使观测器快速收敛的形式[13]为[s-(-ω0)]5（ω0为观测器带宽），令：

可得l。

采用合理设计的扩张状态观测器，简化系统对象为串联积分器的理想形式，可以将控制律中的Te0设计为如下形式：

式中：r为给定值；控制器增益可以选择为为控制器带宽。

3 仿真验证

仿真中所用舵面惯量Jd= 4.36 kg·m2，舵机惯量Jm= 0.872 kg·m2，多级连杆柔性系数Ks=1.872× 105(N·m)/rad。由此可得自然颤振频率ωNTF= 507.557 6 rad/s，扩张状态观测器带宽ω0=12 000 rad/s，控制器带宽ωc=600 rad/s。

首先使用设计的扩张状态观测器观测的总扰动对系统扰动进行消除。总扰动消除前后的开环传递函数如图3所示。总扰动消除前，系统存在一个谐振峰；总扰动消除后，系统谐振峰消失，并且幅频特性曲线每10倍频程下降约80 dB。由此可见，扩张状态观测器性能优异，消除了系统柔性带来的扰动，将系统近似还原为4个积分器串联的标准形式。

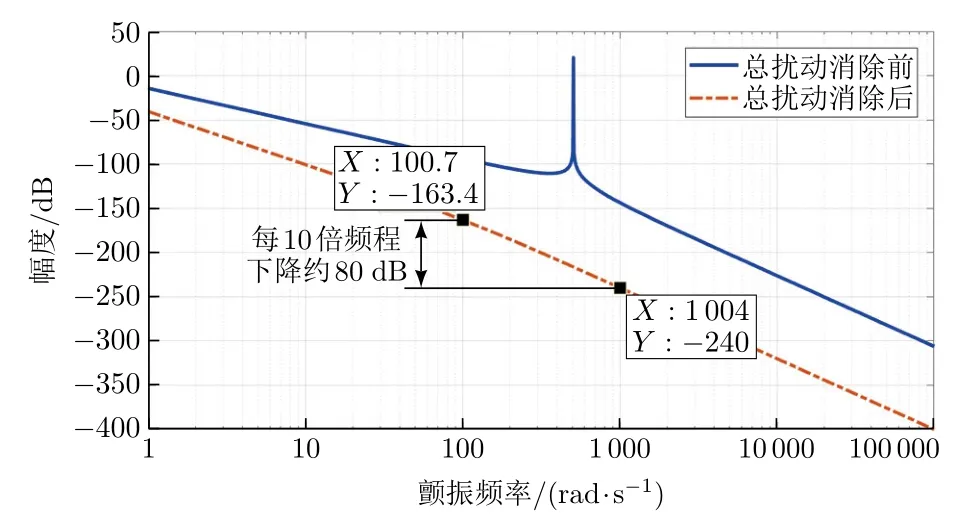
图3 总扰动消除前后的开环传递函数

其次使用设计的扩张状态观测器和控制律进行闭环控制。阶跃指令下自抗扰与比例微分（Proportional Derivative, PD）控制位置响应曲线对比见图4。PD控制响应在0.184 1 s到达9°，并且响应具有颤振；自抗扰控制在0.111 s到达9°，并且响应没有颤振，可见自抗扰控制响应速度快并具有抑制颤振的能力。阶跃指令下扰动及其观测曲线如图5所示，可见观测器能够快速观测到总扰动。自抗扰控制与PD控制闭环幅频特性曲线见图6，PD控制的带宽为29.27 rad/s，并且出现了14.25 dB的谐振峰，自抗扰控制的带宽为267.4 rad/s，可见自抗扰控制带宽大，并且具有消除谐振峰的能力。

图4 阶跃指令下自抗扰与PD控制位置响应曲线

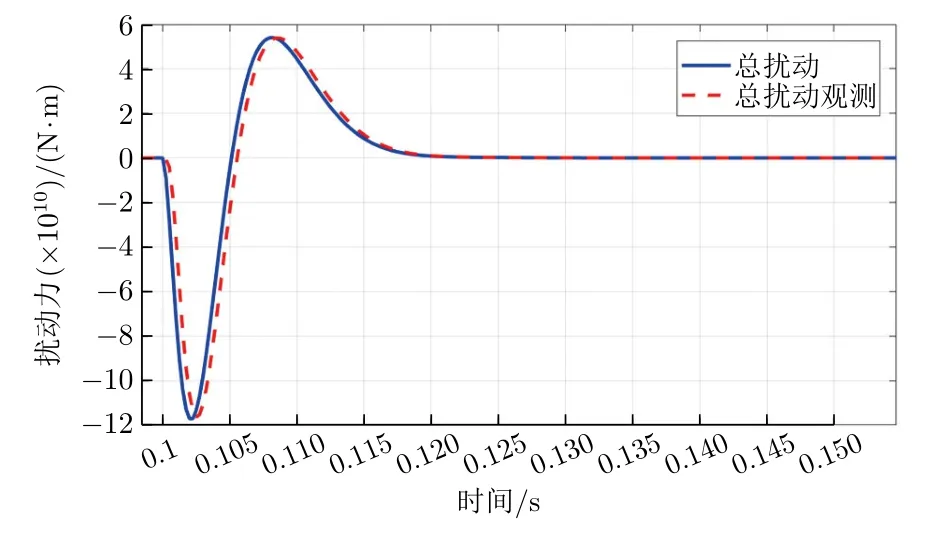
图5 阶跃指令下扰动及其观测曲线

图6 自抗扰控制与PD控制闭环幅频特性曲线

4 结束语

本文首先将无人机柔性多级连杆舵系统建模为一个双惯量柔性系统，然后根据建立的模型进行Matlab仿真分析，发现系统存在柔性导致的谐振峰，用传统的PD控制器进行闭环控制，系统发生颤振。采用自抗扰方法消除颤振，设计了控制策略以及扩张状态观测器。Matlab仿真验证表明，自抗扰控制能够使系统近似为4个积分器串联的形式，通过合理设计控制律可使系统快速响应指令并消除颤振。