考虑尺寸效应的FRP约束混凝土分析模型

管国东, 张璐珂

(1.云南航天工程物探检测股份有限公司，云南 昆明 650217；2.山东大学 岩土与结构工程研究中心，山东 济南 250061)

0 引言

纤维增强复合材料(Fiber Reinforced Polymer，FRP)具有轻质高强、耐腐蚀和不增加截面尺寸等优点，在混凝土墩柱加固中得到广泛应用。FRP约束混凝土改变了混凝土的受力状态，限制了混凝土的侧向变形，极大提高了混凝土的强度。FRP约束柱的力学性能可以通过面向设计的模型[1]与面向分析的模型[2]进行预测。面向设计的模型通常会预设FRP约束混凝土的应力应变曲线形状，然后通过试验数据回归分析标定曲线的特征点(峰值强度、极限强度和极限应变等)[3-5]。设计模型公式简单，便于应用，但不能很好地用于分析FRP约束混凝土的机理，偏重经验性。分析模型通常基于混凝土的轴向压缩和侧向膨胀的关系预测约束应力，再根据约束的应力应变模型预测轴向应力，但通常需要逐步迭代计算。

试验结果表明，混凝土的力学性能随试样尺寸不同而变化，这种特性称为尺寸效应[6]。强度的尺寸效应是混凝土的固有特性，主要产生原因是混凝土内部结构的不均匀性。Bazant[6]建立了一个简化的力学分析模型，探讨混凝土受压破坏时的尺寸效应，但其论文建立的理论和试验测试结果显示：混凝土受压尺寸效应的研究难度较大，其影响因素不仅与混凝土强度相关，还与柱体的破坏形态有密切关系。

关于试件尺寸对FRP约束混凝土构件的混凝土强度影响存在大量研究和争论。Owen[7]首次研究了FRP约束混凝土柱的尺寸效应，发现FRP约束混凝土的极限强度存在显著的尺寸效应。Zhou等[8]对5种不同尺寸的碳纤维布约束混凝土圆柱体进行了轴向压缩试验，试验结果表明，CFRP约束混凝土的极限强度具有明显的尺寸效应，而极限应变只有轻微的尺寸效应。Wang等[9]得出结论，当AFRP约束处于较低水平时，试样尺寸对AFRP约束混凝土的过渡强度和极限强度有显著影响。Jin等[10]通过建立3D细观数值模拟揭示了GFRP约束混凝土存在尺寸效应现象，并建立了极限强度的半经验半理论公式。这些研究工作表明FRP约束混凝土存在尺寸效应。相反，另一些学者[11-15]认为，FRP约束混凝土柱的强度或延性的尺寸效应可以忽略。此外，使用FRP材料加固混凝土结构的现行设计规范(ACI、CAS和fib等)未考虑尺寸效应对约束混凝土材料性能的影响。从上述文献可以看出，关于试件尺寸对约束混凝土的影响存在不同的观点，需要进一步研究。

分析模型从约束混凝土的机理出发，更具理论性，因此选择分析模型开展尺寸效应研究。分析模型中，FRP约束混凝土在复杂应力状态下的行为可以使用Drucker-Prager(以下简称DP)塑性模型进行预测[16-17]。Jamatia等[18]指出Jiang等[17]建立的显式数学模型不能揭示尺寸效应对约束混凝土力学性能的影响。约束混凝土的尺寸效应对强度具有显著的影响，而内聚力本质上是强度的函数，因此本文基于Jiang等的研究基础上通过修正内聚力参数模型来考虑尺寸效应的影响。首先分析了顶部钢板和混凝土圆柱体端部摩擦对破坏模式的影响，然后基于已有文献中的64个样本建立了考虑尺寸效应的内聚力模型，并对模型进行了验证。

1 Jiang等[17]的模型

为了准确预测FRP约束混凝土的应力应变，塑性模型需要具有以下3个特征：①包括第三偏应力不变量的屈服准则；②与围压相关的硬化/软化准则；③流动法则不仅与围压有关，而且与约束增加比率有关。虽然传统的DP塑性模型不包括上述3个特征，但是对DP模型的塑性参数进行修正能够模拟FRP约束混凝土构件在单轴荷载下的应力应变行为[16-17]。这些参数包括：与摩擦角和内聚力相关的参数决定屈服、硬化软化准则，与膨胀角相关的参数决定流动法则。本文采用Jiang等建立的显式参数模型。

1.1 摩擦角模型

(1)

(2)

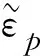
1.2 内聚力模型

(3)

(4)

式中：k为内聚力；fco为无约束混凝土抗压强度；ρ为约束刚度比；p1(ρ)和p2(ρ)为约束刚度比的函数；Efrp为FRP的弹性模量，tfrp为FRP包裹厚度，D为混凝土圆柱体直径。

(5)

(6)

1.3 膨胀角模型

(7)

λ1=11.61ρ+980

(8)

λ2=5 700ρ+225 000

(9)

βu=101.66 exp(-0.06ρ)-37.5

(10)

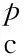
Jamatia等[18]指出Jiang等[17]建立的显式数学模型不能揭示尺寸效应对约束混凝土力学性能的影响，因此，本文对该模型修正以考虑尺寸效应的影响。

2 数值模拟

2.1 有限元模型

采用ABAQUS开展有限元分析。混凝土柱建模为具有适当边界条件的1/8圆柱体。FRP布采用平面应力中的正交异性弹性单层板来定义(Lamina)，只考虑其环向模量，将纵向模量、剪切模量设为无限小，泊松比设置为0.3。混凝土被认为是各向同性材料，采用实体单元C3D8R，见图1。模型底面(即实际构件的中间截面)的Z方向平动，侧面1的Y方向平动和侧面2的X方向平动被约束。模型上端面的钢板与混凝土顶面的相互作用类型为“表面与表面接触”。FRP布和混凝土界面采用ABAQUS 中的“Tie”命令，即FRP布和混凝土无相对滑动。

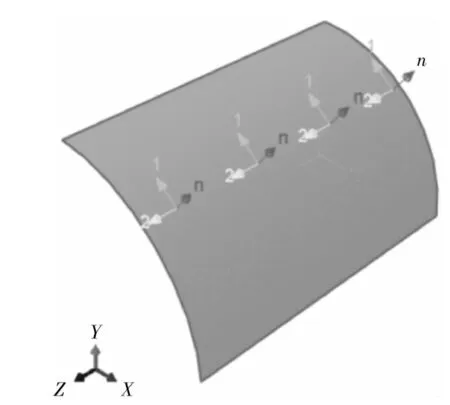
(a)FRP材料局部方向

(b)边界条件

(c)网格划分图1 有限元模型

采用ABAQUS子程序开发的方式开展数值模拟分析。USDFLD子程序可以通过用户自定义的方式将场变量表示成某一变量的函数来定义材料参数。因此采用USDFLD子程序通过定义场变量的方式实现摩擦角、膨胀角和内聚力模型的导入。其中，采用GETVRM子程序来获取材料的积分点信息。

2.2 顶部钢板和混凝土圆柱体端部摩擦对破坏模式的影响

混凝土强度的尺寸效应主要来源于材料的断裂特性，而断裂是材料内部微裂纹发展的结果。Bazant分析了加载端无摩擦情况下的混凝土柱体破坏形式，见图2(a)，这种破坏模式呈现为纵向劈裂裂缝，强度不具有尺寸效应；而当端部存在摩擦时如图2(b)，混凝土柱出现锥体破坏形态，呈现出较多的斜裂缝，这类破坏具有尺寸效应。

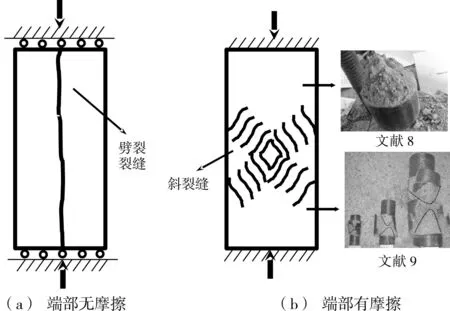
图2 端部摩擦对混凝土破坏模式的影响

从已有的FRP约束混凝土文献调研结果看，目前的试验样本出现了锥体破坏模式。FRP布表面膨胀，变形明显，失效时FRP布断裂，主要原因是，在加载后期内部混凝土的非均匀变形显著，导致FRP材料中的环向应变不均匀。

值得注意的是，Jiang等[17]模型虽然使用了分析模型开展FRP约束混凝土的研究，但是其数值模型中，不考虑顶部加载的端部约束效应(见图2)。然而混凝土圆柱体受压试验，端部不做处理，圆柱体的端面必然存在摩擦。对文献[2]的C38CF4样本进行计算，样本的具体参数参见表1。图3为不同摩擦系数下混凝土的轴向塑性应变云图。

由图3可知：考虑端部摩擦，锥体破坏可以较好地被模拟；而Jiang等[17]得到的结果，如图3(a)，不能出现典型的锥体破坏模式。文献[19]给出钢板和混凝土摩擦系数为0.6，本文采用该值作为ABAQUS相互作用表面接触中摩擦系数。

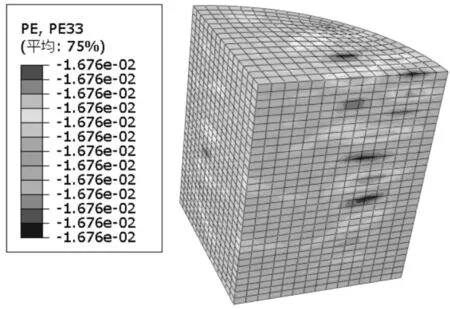
(a)摩擦系数0

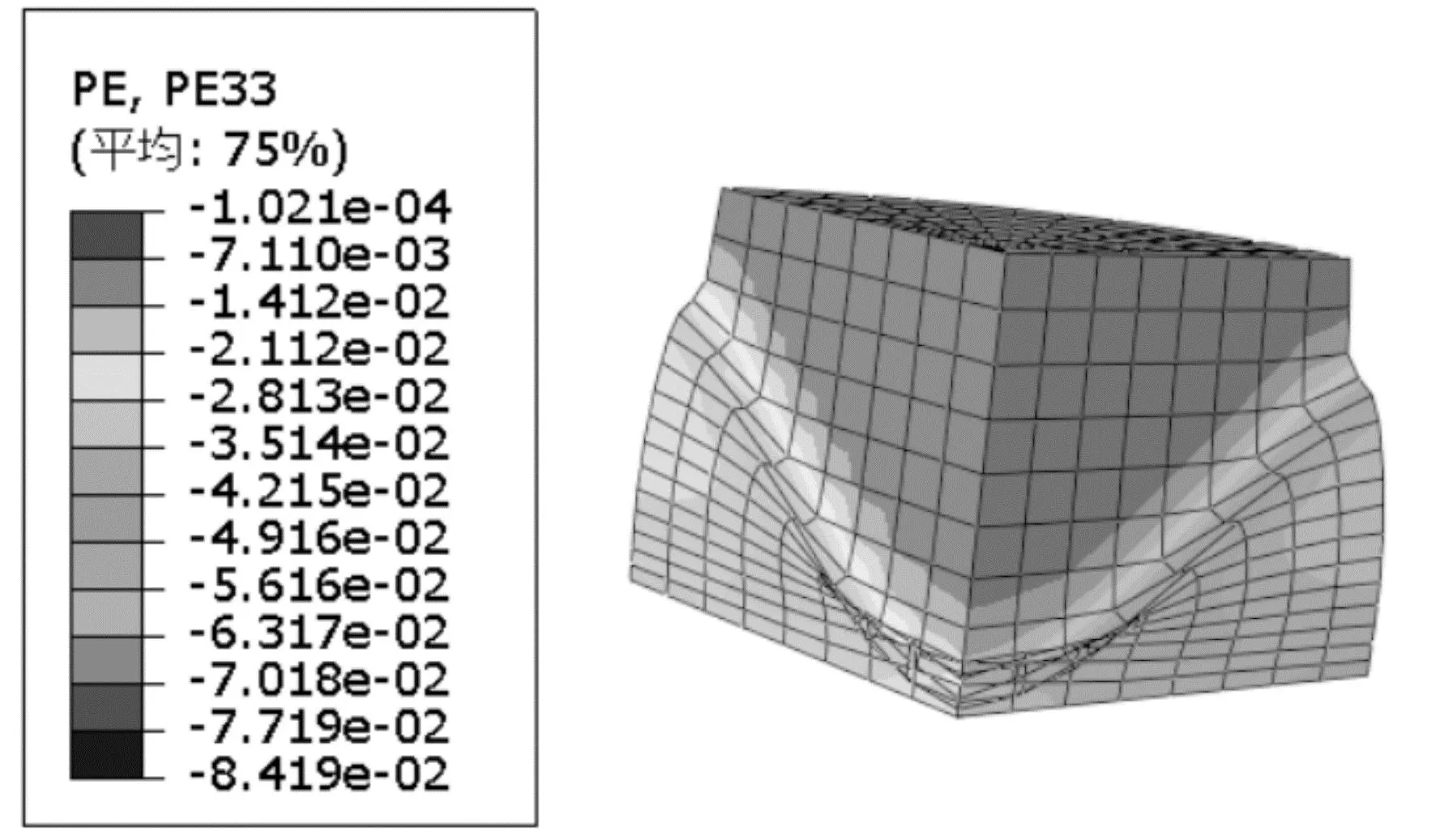
(b)摩擦系数0.6

(c)摩擦系数1图3 不同摩擦系数下约束混凝土轴向塑性应变云图

3 结果分析

3.1 拟合样本介绍

本文收集了相关文献中的64个样本(见表1)，包括不同的FRP材料、混凝土抗压强度、圆柱体直径和高度、FRP粘贴层数。需要说明的是，编号带上标a的试验样本，参考文献并没有对应的编号，本文是根据无约束混凝土圆柱体抗压强度fco、FRP种类和包裹层数命名的。例如，C39.6GF1表示无约束混凝土圆柱体抗压强度为39.6 MPa、FRP材料为玻璃纤维、包裹层数为1层，其余样本编号均采用参考文献中试件编号。fcu1(FEA)通过式(3)得到,fcu2(FEA)通过后文中式(11)得到。

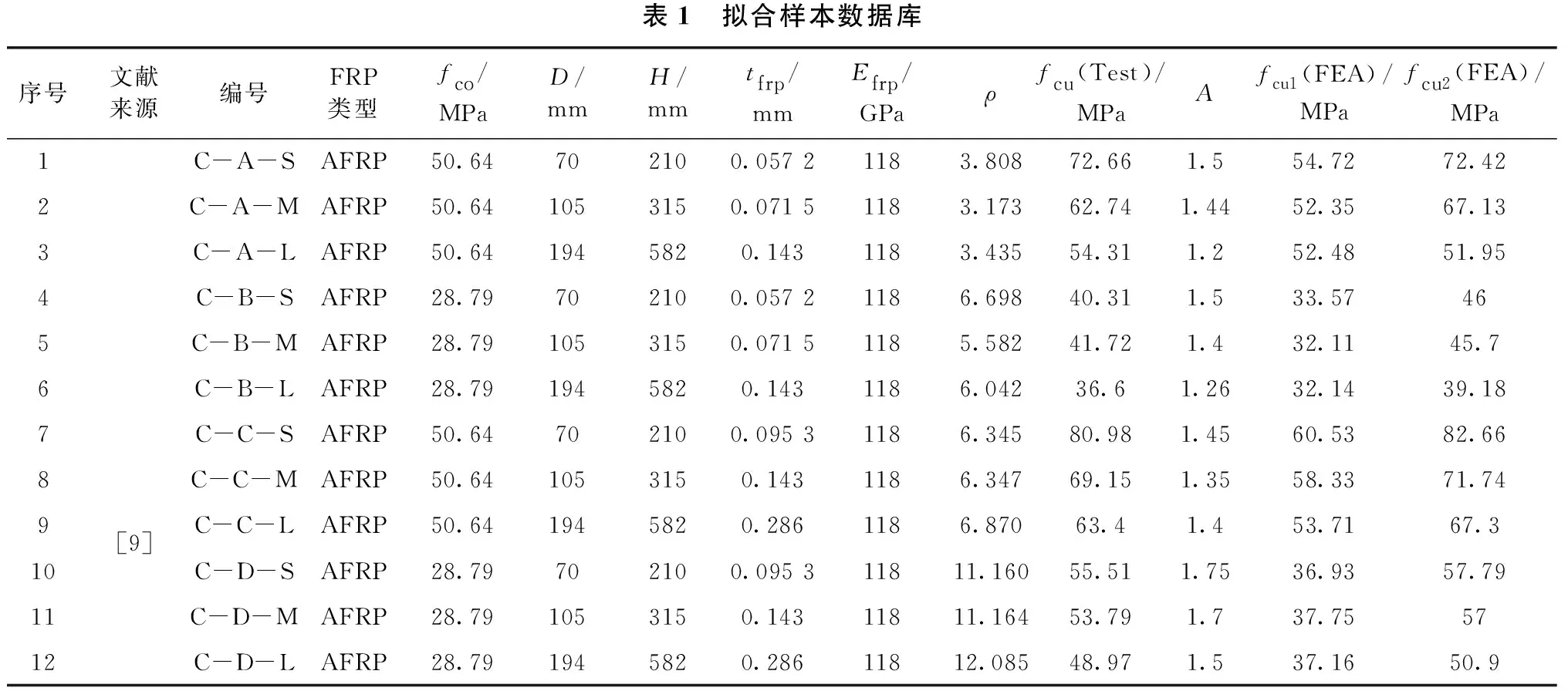
表1 拟合样本数据库序号文献来源编号FRP类型fco/MPaD/mmH/mmtfrp/mmEfrp/GPaρfcu(Test)/MPaAfcu1(FEA)/MPafcu2(FEA)/MPa1C-A-SAFRP50.64702100.057 21183.808 72.661.554.7272.422C-A-MAFRP50.641053150.071 51183.173 62.741.4452.3567.133C-A-LAFRP50.641945820.1431183.435 54.311.252.4851.954C-B-SAFRP28.79702100.057 21186.698 40.311.533.57465C-B-MAFRP28.791053150.071 51185.582 41.721.432.1145.76C-B-LAFRP28.791945820.1431186.042 36.61.2632.1439.187C-C-SAFRP50.64702100.095 31186.345 80.981.4560.5382.668C-C-MAFRP50.641053150.1431186.347 69.151.3558.3371.749[9]C-C-LAFRP50.641945820.2861186.870 63.41.453.7167.310C-D-SAFRP28.79702100.095 311811.160 55.511.7536.9357.7911C-D-MAFRP28.791053150.14311811.164 53.791.737.755712C-D-LAFRP28.791945820.28611812.085 48.971.537.1650.9

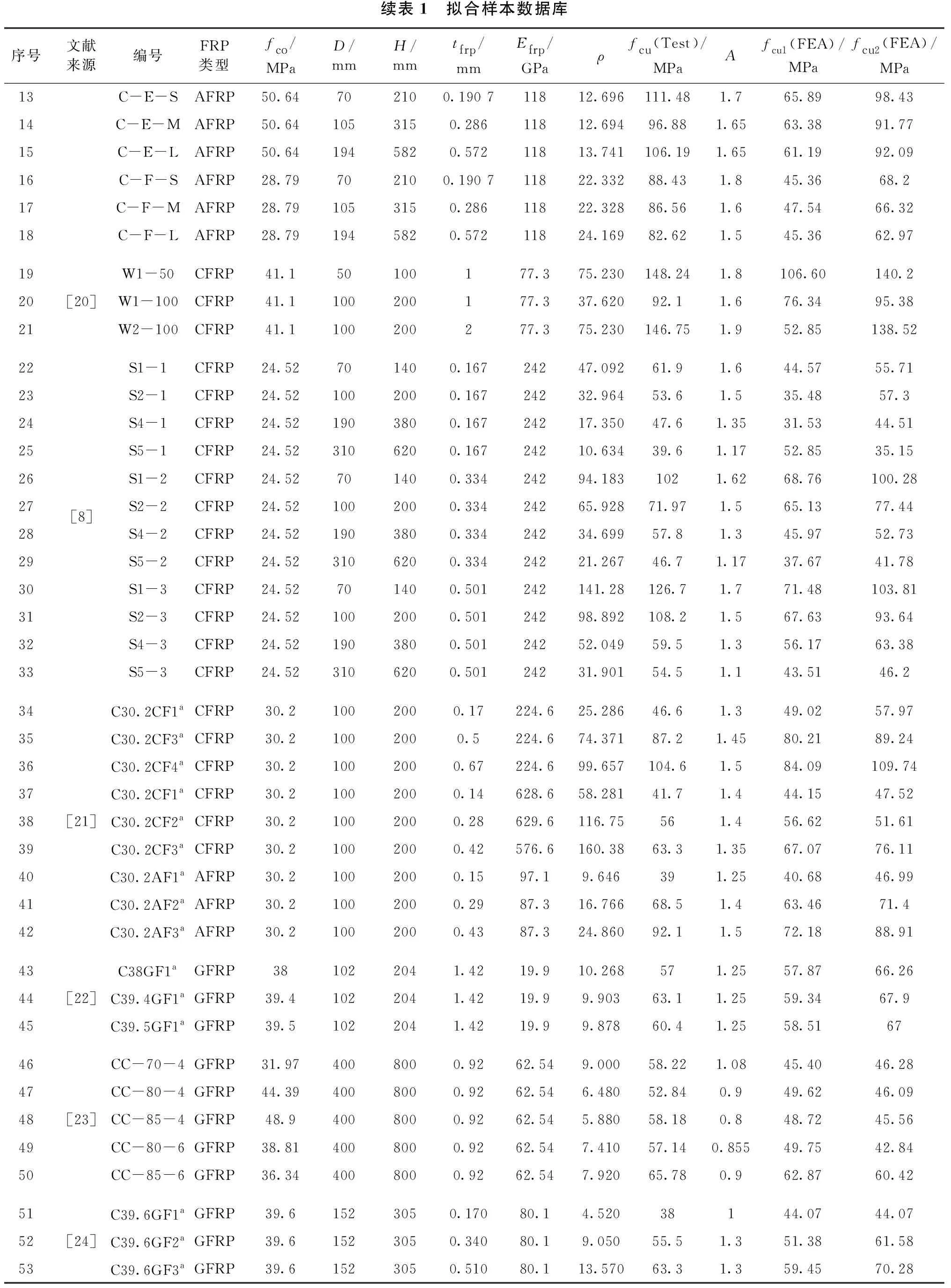
续表1 拟合样本数据库序号文献来源编号FRP类型fco/MPaD/mmH/mmtfrp/mmEfrp/GPaρfcu(Test)/MPaAfcu1(FEA)/MPafcu2(FEA)/MPa13C-E-SAFRP50.64702100.190 711812.696 111.481.765.8998.4314C-E-MAFRP50.641053150.28611812.694 96.881.6563.3891.7715C-E-LAFRP50.641945820.57211813.741 106.191.6561.1992.0916C-F-SAFRP28.79702100.190 711822.332 88.431.845.3668.217C-F-MAFRP28.791053150.28611822.328 86.561.647.5466.3218C-F-LAFRP28.791945820.57211824.169 82.621.545.3662.9719W1-50CFRP41.150100177.375.230148.241.8106.60140.220[20]W1-100CFRP41.1100200177.337.62092.11.676.3495.3821W2-100CFRP41.1100200277.375.230146.751.952.85138.5222S1-1CFRP24.52701400.16724247.09261.91.644.5755.7123S2-1CFRP24.521002000.16724232.96453.61.535.4857.324S4-1CFRP24.521903800.16724217.35047.61.3531.5344.5125S5-1CFRP24.523106200.16724210.63439.61.1752.8535.1526S1-2CFRP24.52701400.33424294.1831021.6268.76100.2827[8]S2-2CFRP24.521002000.33424265.92871.971.565.1377.4428S4-2CFRP24.521903800.33424234.69957.81.345.9752.7329S5-2CFRP24.523106200.33424221.26746.71.1737.6741.7830S1-3CFRP24.52701400.501242141.28126.71.771.48103.8131S2-3CFRP24.521002000.50124298.892108.21.567.6393.6432S4-3CFRP24.521903800.50124252.04959.51.356.1763.3833S5-3CFRP24.523106200.50124231.90154.51.143.5146.234C30.2CF1aCFRP30.21002000.17224.625.28646.61.349.0257.9735C30.2CF3aCFRP30.21002000.5224.674.37187.21.4580.2189.2436C30.2CF4aCFRP30.21002000.67224.699.657104.61.584.09109.7437C30.2CF1aCFRP30.21002000.14628.658.28141.71.444.1547.5238[21]C30.2CF2aCFRP30.21002000.28629.6116.75561.456.6251.6139C30.2CF3aCFRP30.21002000.42576.6160.3863.31.3567.0776.1140C30.2AF1aAFRP30.21002000.1597.19.646391.2540.6846.9941C30.2AF2aAFRP30.21002000.2987.316.76668.51.463.4671.442C30.2AF3aAFRP30.21002000.4387.324.86092.11.572.1888.9143C38GF1aGFRP381022041.4219.910.268571.2557.8766.2644[22]C39.4GF1aGFRP39.41022041.4219.99.90363.11.2559.3467.945C39.5GF1aGFRP39.51022041.4219.99.87860.41.2558.516746CC-70-4GFRP31.974008000.9262.549.00058.221.0845.4046.2847CC-80-4GFRP44.394008000.9262.546.48052.840.949.6246.0948[23]CC-85-4GFRP48.94008000.9262.545.88058.180.848.7245.5649CC-80-6GFRP38.814008000.9262.547.41057.140.85549.7542.8450CC-85-6GFRP36.344008000.9262.547.92065.780.962.8760.4251C39.6GF1aGFRP39.61523050.17080.14.52038144.0744.0752[24]C39.6GF2aGFRP39.61523050.34080.19.05055.51.351.3861.5853C39.6GF3aGFRP39.61523050.51080.113.57063.31.359.4570.28

3.2 尺寸效应修正内聚力模型

ABAQUS 扩展DP准则中，摩擦角、内聚力和膨胀角参数控制混凝土应力应变行为，尺寸效应对强度具有显著影响，内聚力本质上是剪切强度，因此对内聚力修正是合理的。考虑到混凝土抗拉和抗压强度均存在尺寸效应[6]，仅仅考虑修正内聚力参数考虑尺寸效应的影响。对式(3)增加修正系数A，该系数和混凝土圆柱体尺寸产生关联，进而建立考虑尺寸效应的修正模型，见式(11)。

(11)

考虑论文篇幅，仅仅显示6个拟合样本预测值和试验值的对比结果，见图4，图4中样本编号参见表 1。从图4可以看出：采用内聚力修正系数修正后，应力应变曲线和实测值比修正前更为吻合。

(a) C-A-SS

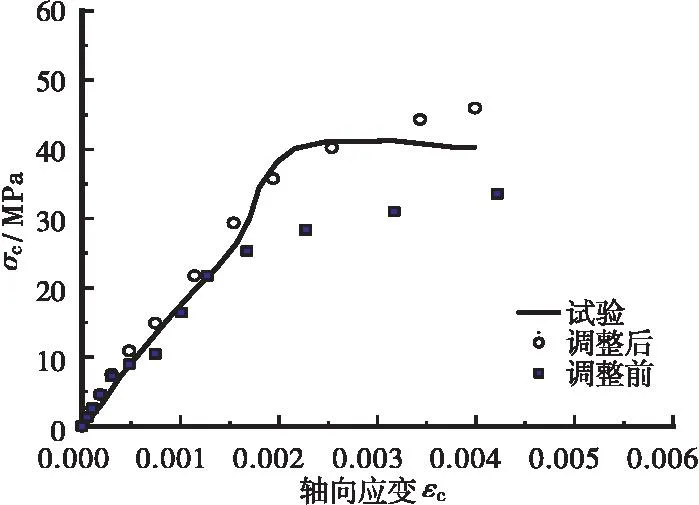
(b) C-B-S

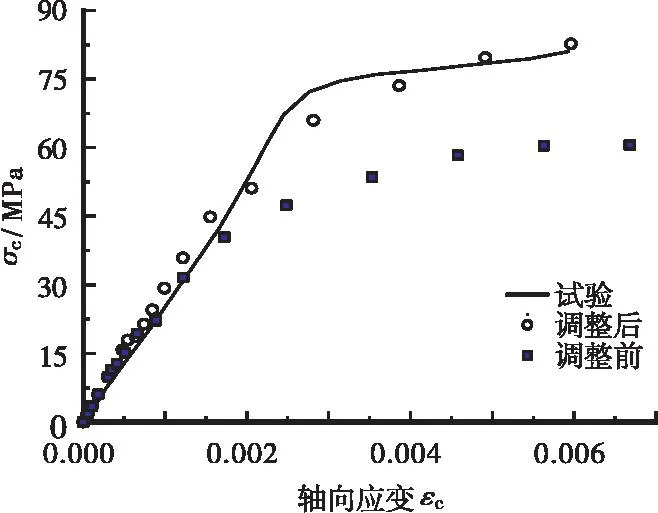
(c) C-C-S

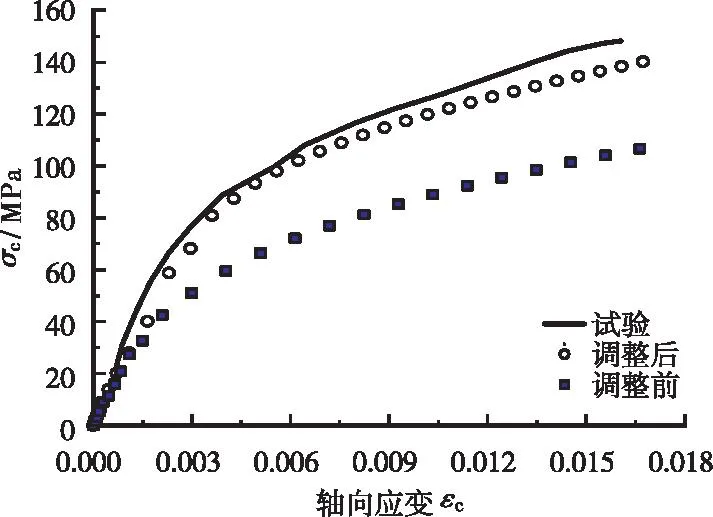
(d)W1-50

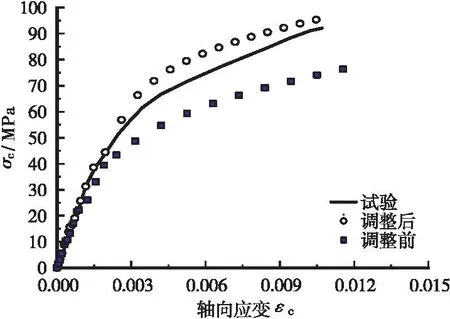
(e) W1-100

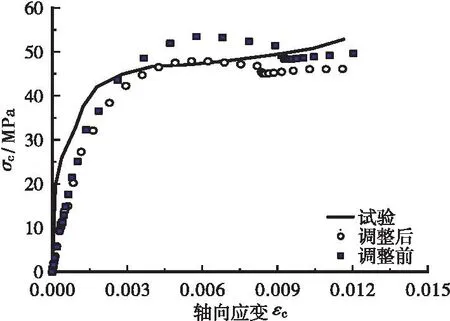
(f) CC-80-4图4 拟合样本FEA值和试验值应力应变曲线对比

统计64个样本的名义强度预测值和试验值的对比结果见图5，从图中可以看出，64个拟合样本的试验值与理论预测值具有较好的一致性，R2=0.91，表明本文采用的修正方法能较好地模拟不同圆柱体直径对FRP约束混凝土柱名义抗压强度的影响。

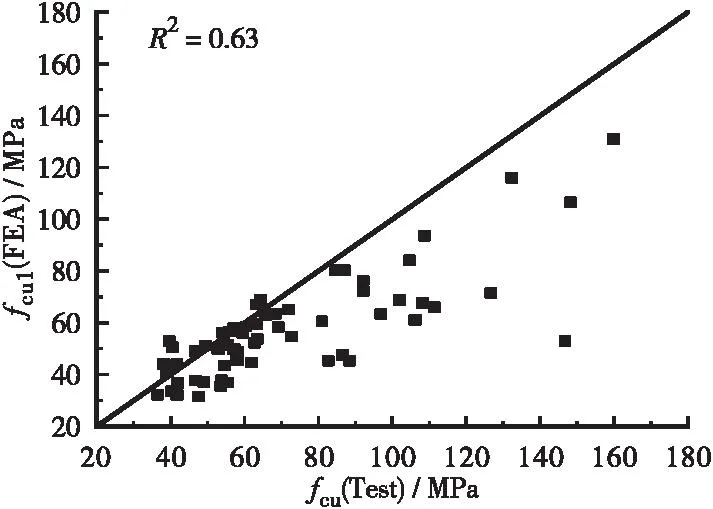
(a)修正前

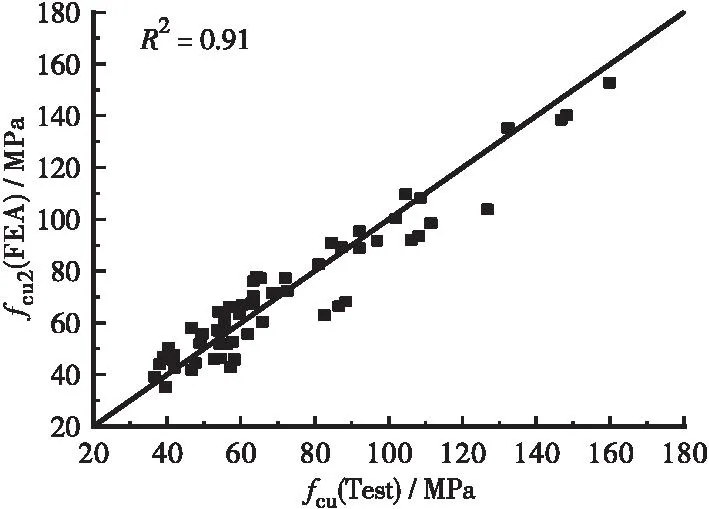
(b)修正后图5 拟合样本极限强度试验值与FEA对比

Bazant提出了尺寸效应定律，见式(12)。

Kim等[25]认为对于约束混凝土圆柱体，式(12)中的D可以用高度与直径的差值(H-D)代替,因为混凝土柱的能量释放主要在试样中间高度附近的(H-D)区域观察到。

(12)

式中：σNu为圆柱体试件的名义强度；B、D0为依赖于结构的几何常数；D为圆柱体试件的直径。

因此，本文，见式(13)和式(14)。

(13)

(14)

式中：a和b为待定系数。

表1中的64个样本涵盖了50～400 mm直径的不同样本。统计64个拟合样本的修正系数A和试件直径D，确定待定系数a和b(见图6)。

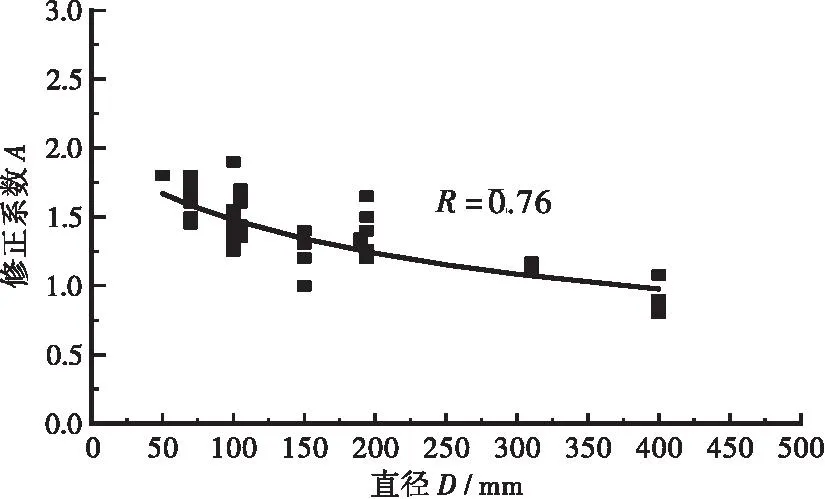
(a)式(13)计算所得修正系数

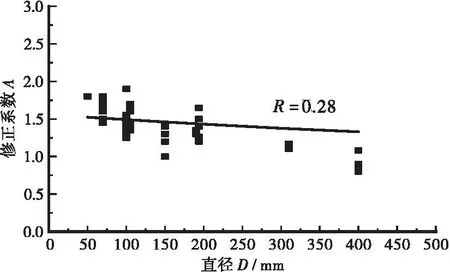
(b)式(14)计算所得修正系数图6 考虑尺寸效应的内聚力修正系数形式对比

由图6对比可得，式(14)的内聚力修正系数拟合效果最优，其相关系数R=0.76。从结果看，内聚力修正系数存在一定的离散性，主要原因是锥体破坏模式和试验破坏形态之间存在一定的偏差，理论模型一定程度上不能完全展示试验样本的各种破坏形态。将式(13)代入式(11)，得到考虑尺寸效应的内聚力模型，如式(15)所示。

(15)

3.3 模型验证

为了验证本文提出的修正模型，进一步收集了不同文献的试验测试结果，共25个样本。具体验证样本信息参见表2。

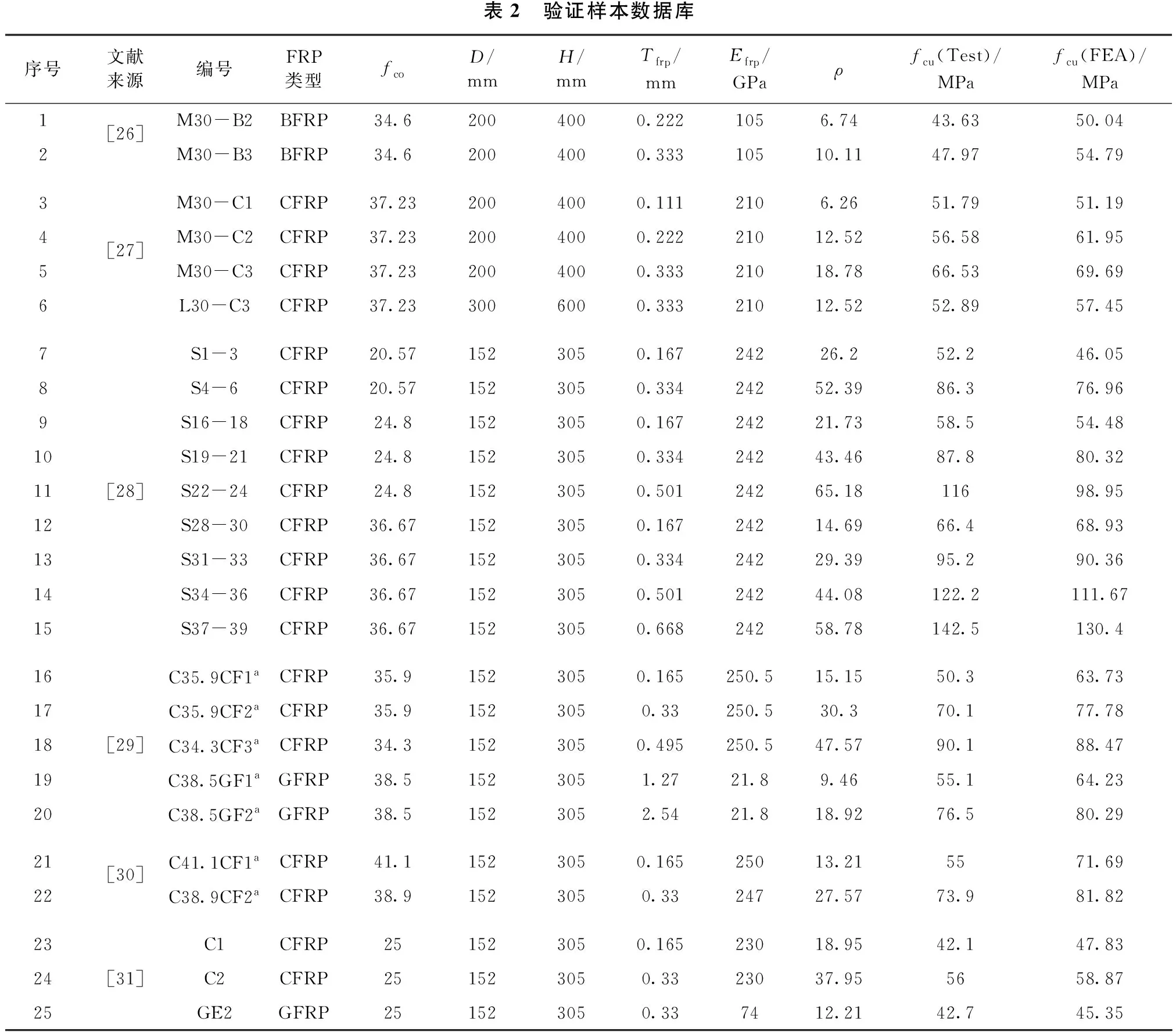
表2 验证样本数据库序号文献来源编号FRP类型fcoD/mmH/mmTfrp/mmEfrp/GPaρfcu(Test)/MPafcu(FEA)/MPa1[26]M30-B2BFRP34.62004000.2221056.7443.6350.042M30-B3BFRP34.62004000.33310510.1147.9754.793M30-C1CFRP37.232004000.1112106.2651.7951.194[27]M30-C2CFRP37.232004000.22221012.5256.5861.955M30-C3CFRP37.232004000.33321018.7866.5369.696L30-C3CFRP37.233006000.33321012.5252.8957.457S1-3CFRP20.571523050.16724226.252.246.058S4-6CFRP20.571523050.33424252.3986.376.969S16-18CFRP24.81523050.16724221.7358.554.4810S19-21CFRP24.81523050.33424243.4687.880.3211[28]S22-24CFRP24.81523050.50124265.1811698.9512S28-30CFRP36.671523050.16724214.6966.468.9313S31-33CFRP36.671523050.33424229.3995.290.3614S34-36CFRP36.671523050.50124244.08122.2111.6715S37-39CFRP36.671523050.66824258.78142.5130.416C35.9CF1aCFRP35.91523050.165250.515.1550.363.7317C35.9CF2aCFRP35.91523050.33250.530.370.177.7818[29]C34.3CF3aCFRP34.31523050.495250.547.5790.188.4719C38.5GF1aGFRP38.51523051.2721.89.4655.164.2320C38.5GF2aGFRP38.51523052.5421.818.9276.580.2921[30]C41.1CF1aCFRP41.11523050.16525013.215571.6922C38.9CF2aCFRP38.91523050.3324727.5773.981.8223C1CFRP251523050.16523018.9542.147.8324[31]C2CFRP251523050.3323037.955658.8725GE2GFRP251523050.337412.2142.745.35

25个验证样本的极限强度试验和FEA对比结果如见图7所示，其理论预测值和试验测试值的R2=0.93，表明了本文修正的内聚力模型能够有效揭示FRP约束混凝土圆柱体的抗压强度尺寸效应。

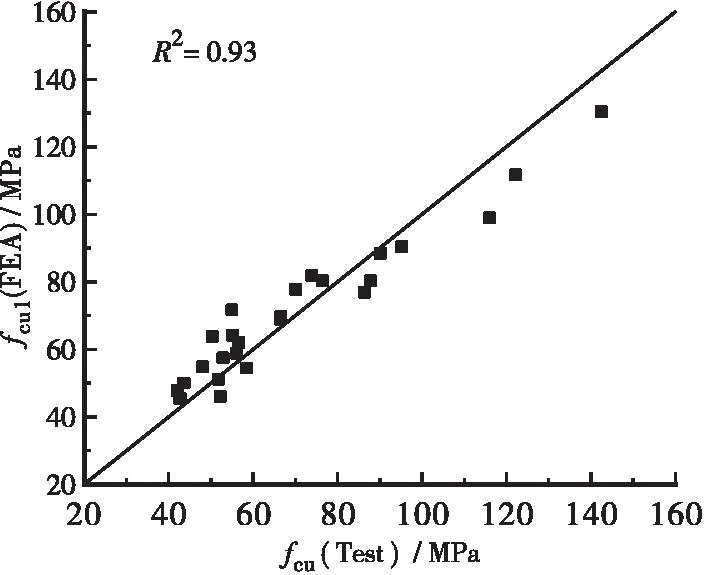
图7 验证样本极限强度试验和FEA对比

4 结论

通过试验分析和数值模拟考虑尺寸效应对FRP约束混凝土的影响，得到以下结论：

1)考虑顶部钢板和混凝土圆柱体的端部摩擦，能够较好地模拟FRP约束混凝土圆柱体试件的锥体破坏模式。

2)基于ABAQUS的USDFLD子程序，通过内聚力修正系数A考虑尺寸效应的影响，见式(13)。建立了考虑尺寸效应的内聚力模型，见式(15)。对内聚力模型进行了验证，极限强度的试验值和FEA值决定系数R2=0.93，表明所提出内聚力模型的正确性。

3)本文提出的模型具有一定局限性：拟合样本和验证样本均为圆形截面混凝土柱，对于其它截面(矩形和方形)，需要考虑不均匀约束的影响。