跨音速槽道流中绝热气膜冷却效率的求解方法

2024-01-01刘一粟戴思明李家宁马海腾

动力工程学报 2023年12期

关键词：统计法冷气气膜

刘一粟, 曾伟, 戴思明, 李家宁, 马海腾

(上海交通大学机械与动力工程学院,上海 200240)

符号说明:

η——绝热气膜冷却效率

T——温度,K

p——压力,kPa

Ma——马赫数

D——气膜孔直径,mm

Re——雷诺数

M——吹风比

k——线性拟合的斜率

σ——标准差

h——对流传热系数,W/(m2·K)

qm——质量流量,kg/s

q——壁面热流密度,W/m2

U——不确定度,%

W——红外视野长度,mm

下标

0——滞止参数

is——等熵

t——测试段

aw——绝热壁面

w——壁面

c——有冷

uc——无冷

r——恢复参数

s——静参数

in——主流入口

ref——参考值

随着航空发动机推力与热效率不断提升,涡轮进口温度也在不断上升。现代航空发动机涡轮进口温度可达2 000 K,远超涡轮叶片材料熔点[1]。为防止涡轮叶片被高温燃气烧毁,冷却技术被应用于涡轮叶片中。自20世纪70年代涡轮叶片引入气膜冷却技术以来,这项技术已经成为提升航空发动机性能与使用寿命的关键技术。

气膜冷却的原理是气膜孔喷射出的低温冷气附着在壁面形成一层冷气膜,这层冷气膜将壁面与高温燃气分隔开来,以降低壁面与高温燃气的换热量,达到保护壁面的目的[2]。气膜冷却的机理十分复杂,气膜冷却的效果受到冷气与主流参数(温比和吹风比等)、气膜孔几何构型以及气膜孔分布等参数的影响[3-6],难以通过理论分析或数值计算精准预测其效果。因此,工程上普遍在实验室中开展气膜冷却模化实验,以此来检验冷却设计的实际效果。而随着发动机负荷不断增加,涡轮叶片部分区域流场达到跨音速状态,流场结构极为复杂,如何通过模化实验准确检验跨音速流中气膜冷却的效果成为业界关注的焦点。绝热气膜冷却效率η是描述气膜冷却效果的重要参数,其定义式为:

(1)

与低速实验选取主流温度T∞作为参考温度不同,跨音速流动中由于边界层内的黏性加热作用[7],参考温度通常选取为恢复温度Tr。恢复温度与流场结构有关[8],实验中获取其分布结果较为困难,为解决这一问题,现存在2种绝热气膜冷却效率定义式中恢复温度的确定方法。

第一种是由O'Dowd等[9]提出的LRM(liner regression method),该方法定义绝热气膜冷却效率中的恢复温度为无冷实验的绝热壁温Taw,uc。因此,绝热气膜冷却效率的定义式变为:

(2)

即绝热气膜冷却效率由无冷和有冷实验共同确定。因为该方法给出的恢复温度的物理定义十分明确,故在本文中称该方法为物理法。目前,物理法已被广泛应用于流场结构复杂的跨音涡轮叶片叶尖区域的冷却特性实验研究中。O'Dowd等[9]采用此方法研究了跨音小翼叶尖的气膜冷却特性,发现降低叶尖间隙能提高叶尖区域气膜冷却效率。王维杰等[10]采用物理法研究了高压涡轮尾切凹槽的冷却特性。Ma等[11]研究了平叶尖气膜冷却与激波的相互作用,发现与无冷实验相比冷却气膜改变了叶尖间隙内的激波结构。

第二种方法是Xue等[12]提出的DLRT(dual liner regression technique)。该方法认为对于仅冷气温度存在差别的有冷实验来说,它们的对流传热系数、气膜冷却效率应当相同。通过对2组冷气温度不同的有冷实验数据进行迭代寻优,找到满足上述观点的最佳恢复温度值。因为该方法具有统计特性,因此在本文中该方法被称为统计法。目前,统计法已被应用在涡轮叶片各个区域的冷却特性研究中。Arisi等[13]将统计法应用到尾部带肋条的凹槽叶尖冷却特性研究中,结果表明压力侧肋条的阻塞作用对其下游的气膜冷却效果有不利影响。Hossain等[14]采用统计法研究了跨音速流中带有振荡器的气膜冷却结构与7-7-7孔在不同吹风比下的气膜冷却特性。Xue等[15]应用统计法研究了气膜冷却与激波的相互作用,发现激波在反射处形成的二次流会降低气膜冷却效率。Ma等[16]在跨音速理想叶尖模型中比较了物理法与统计法的区别,发现两者获得的绝热气膜冷却效率有很大差别。

综上所述,有学者采用物理法和统计法进行跨音速气膜冷却实验研究,但并未深入研究2种方法的区别。现有文献仅在理想叶尖模型这类狭缝流中比较过两者的区别,而涡轮叶片端壁、压力侧与吸力侧的流动与狭缝流的差别较大,因此狭缝流得到的结论无法推广至上述区域。为了进一步研究物理法与统计法在此类流动中的区别,笔者搭建了跨音速槽道流实验台,开展了不同主流温度和冷气温度下的无冷和有冷实验,分析比较了2种方法获得的对流传热系数和绝热气膜冷却效率差异。

1 实验介绍

1.1 实验系统

跨音速槽道流实验系统如图1所示。该系统由上海交通大学气动换热实验室的暂冲式风洞改进而来。实验系统由储气罐、控制阀、加热丝网、喷管、实验测试段、预冷冷气系统和实验测量系统构成。储气罐可储存10 m3最大压力为3 MPa的压缩空气。实验时压缩空气经主阀门通入实验测试段,其压力由主阀门的开度控制。通过主阀门后的压缩空气经过蜂窝器整流后被功率为100 kW的加热丝网加热,其温度提升至目标温度。温升后的主流质量流量qm,in可由位于收缩段出口的皮托管测得的总压p0,in、静压ps,in和总温度探针(Omega T型热电偶,精度为±0.5 K)测得的总温T0,in计算得出。随后,主流进入拉法尔喷管进行加速,通过测试段之后在扩压管中减速并被排入大气。实验系统的更多细节参见文献[17]。

图1 实验系统简图

如图1所示,预冷冷气系统由压力控制阀、涡流管、过滤器、质量流量控制器、缓冲箱和冷气室构成。通入冷气系统的压缩空气的压力被压力控制阀(CKD 23026C)稳定在0.7 MPa。为增大冷气与主流的温差,采用涡流管(AirTx, No. 24015)对冷气进行降温,冷气中凝结的水汽由调压过滤器(SFR2000)除去。冷气质量流量qm,c由质量流量控制器(ALICAT, 250 SLPM Flow Controller)控制在设定值。最后,冷气进入缓冲箱,测得其压力pc与温度Tc后再进入测试段。为防止冷气与外界发生热交换,冷气系统管路均采用保温棉进行隔热保温处理。正式实验开始前,对测试件预冷30 min,保证其处于热稳定状态。

1.2 测试段与测试件

测试段结构如图 2(a)所示,测试段长度为200 mm,宽度为46.4 mm,进口高度为23.2 mm,为防止边界层对流场产生影响,测试段上壁面与水平的倾角为0.5°。在测试段上表面开设红外视窗,FLIR A655 sc(分辨率640×484,频率50 Hz)红外相机可透过红外玻璃(CaF2)拍摄测试件表面温度随时间的变化。红外相机视野范围如图 2(b)(其中W≈45D)所示,其拍摄范围可覆盖气膜孔上游约10D以及气膜孔下游约35D的区域。

测试件分为无冷件与有冷件2种,均由相同的低热导率(0.02 W/(m·K))尼龙材料制成,厚度为30 mm。为获取测试段内等熵马赫数Mais分布,在测试件表面沿流动方向均匀布置了多个直径为0.7 mm的静压测试孔,以获得测试段内静压ps,t数据。无冷件表面无任何冷却结构;有冷件表面开设有直径为1 mm的圆形气膜孔,孔结构如图2(c)所示,倾斜角为30°,长径比为10,孔间距为4.4D。为保证周期性,有冷件共开设9个气膜孔。

(a) 测试段剖视图

1.3 实验工况

实验工况如表1所示,为保证实验结果的准确性,无冷和有冷实验在每个工况点均重复了4次。

表1 实验工况

采用红外相机获取壁面温度随时间变化的数据。为保证红外相机测得壁面温度的准确性,正式实验前需对相机进行校准。校准方法为利用薄膜电加热片在恒定功率下加热一块与测试件材料相同的薄片,薄片表面布置有热电偶,可以对温度进行实时检测。当薄片达到热稳态后,记录红外相机获得的表面灰度数据与热电偶测得的表面温度数据。随后关闭电源,并记录薄片在自然冷却过程中的数据,用于后续验证。对热稳态时的灰度值与温度数据进行修正,结果如图3所示,数据的线性回归系数R2接近1,最终可得红外测温误差在-1.5～1.5 K内。

图3 红外相机灰度值校准

2 数据获取与处理方法

2.1 数据获取

实验过程中压力、温度以及红外视频数据均通过NI MAX程序获取并实时显示在基于LabVIEW语言自主编写的可视化界面上。主流和冷气的温度与压力随时间的变化如图4所示。实验开始时打开主阀门,待主流压力稳定后打开加热丝网,使主流总温阶跃提升至目标温度。选取参数稳定时间2 s来计算表面传热系数和绝热壁温,并选取具有代表性的中心三孔区域作为数据处理区(如图2(b)所示)。

图4 主流与冷气的温度和压力随时间的变化

2.2 物理法实验数据处理

O'Dowd等[9]提出的物理法认为绝热气膜冷却效率定义式中恢复温度等于无冷工况的恢复温度,即无冷工况的绝热壁温。由无冷工况的牛顿冷却公式可得:

q=h(Taw,uc-Tw)

(3)

对上式进行变换可得:

q=-hTw+hTaw,uc

(4)

其中,壁面热流密度基于一维半无限大平板假设,采用Oldfield[18]提出的利用离散信号的卷积与反卷积算法处理得到。对每个像素点壁面温度Tw及壁面热流密度q的数据进行如图5所示的线性回归处理。由回归直线的斜率与截距即可求得对流传热系数和无冷工况的绝热壁温。

图5 物理法实验数据处理

由图5可得,对于有冷实验来说,在阶跃温升区域内主流与冷气温度均可认为是不变的,主流与冷气的流动是稳定的。因此,由主流和冷气共同确定的有冷绝热壁温保持不变,对有冷工况牛顿冷却公式变换可得:

q=-hTw+hTaw,c

(5)

对壁面热流密度与壁面温度数据进行线性回归,即可得到有冷工况的对流传热系数与绝热壁温。最后,将无冷工况的绝热壁温与有冷工况的绝热壁温代入定义式(2)即可得到绝热气膜冷却效率。有关物理法的更多细节参见文献[11]。

2.3 统计法实验数据处理

Xue等[12]提出的统计法认为对于主流热力与气动条件相同,吹风比相同,仅冷气温度有差别的实验而言,其对流传热系数、绝热气膜冷却效率应当一致。基于上述观点,牛顿冷却公式可变换为:

(6)

其中,

(7)

式(6)中壁面热流密度q的获取方法与物理法一致。而恢复温度Tr为未知量,需要对2组仅冷气温度不同的有冷实验数据进行迭代以寻找最优值,使得q/(Tr-Tc)与(Tr-Tw)/(Tr-Tc)数据线性回归得到的直线斜率、截距相同,其结果如图6所示,其中直线斜率为对流传热系数,截距与斜率之比的绝对值为绝热气膜冷却效率。

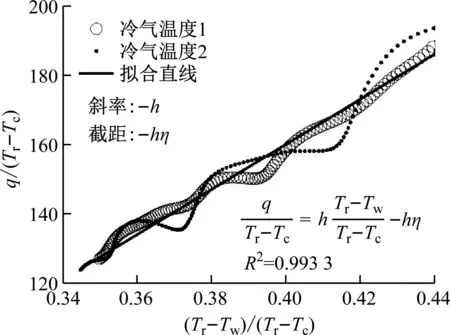
图6 统计法寻找的最优恢复温度

2.4 不确定度分析

物理法与统计法的线性拟合优劣可由拟合不确定度U(基于95%置信区间)来评价[16-17]。拟合不确定度的计算方法如式(8)所示,式中x在物理法中为Tw,而在统计法中为(Tr-Tw)/(Tr-Tc),N为数据点个数,σ为拟合结果的标准差,σk为拟合直线斜率的标准差,k为拟合直线的斜率。单次实验中每个像素点平均后的拟合不确定度如表2所示。结果表明无冷实验中主流温度越高,实验数据拟合结果的不确定度越低;有冷实验中低温冷气得到的不确定度较低。与物理法相比,统计法使用2组有冷数据,拟合不确定度远低于物理法。

(8)

表2 单次实验拟合平均不确定度

物理法与统计法在每个工况点获得的4组结果的重复性误差(t分布,95%置信度)如表3所示,结果同样表明统计法获得的对流传热系数更加准确。需要说明的是,最终实验结果是2组结果的平均值。

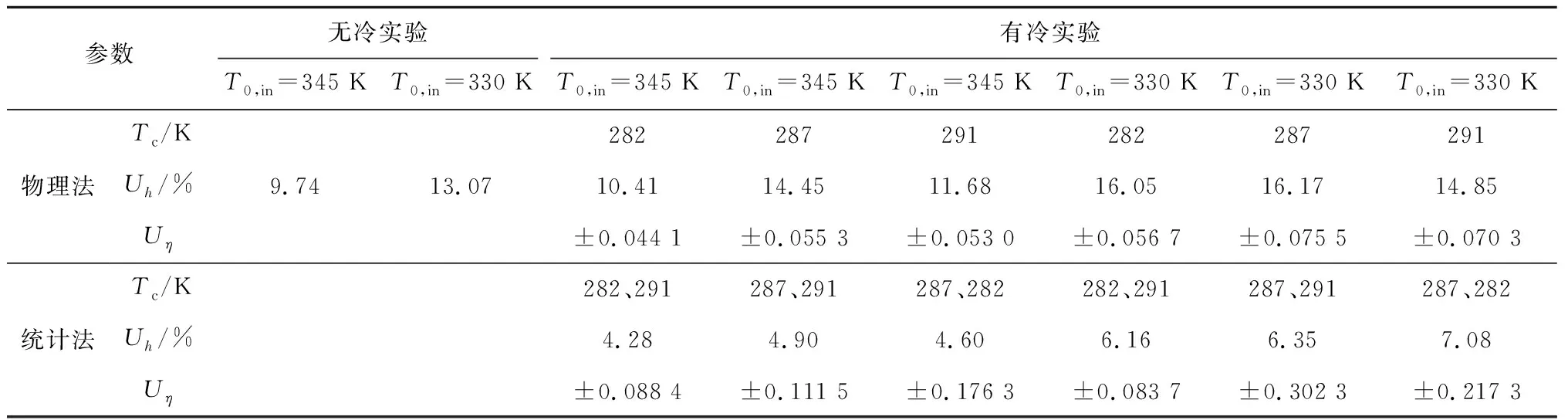
表3 实验不确定度分析

3 结果与分析

3.1 对流传热系数

物理法和统计法获得的对流传热系数分布如图7所示。2种方法处理得到的结果表明由于冷气射流的剧烈扰动,气膜孔的附近区域形成了高传热区。主流温度对对流传热系数的分布几乎无影响。

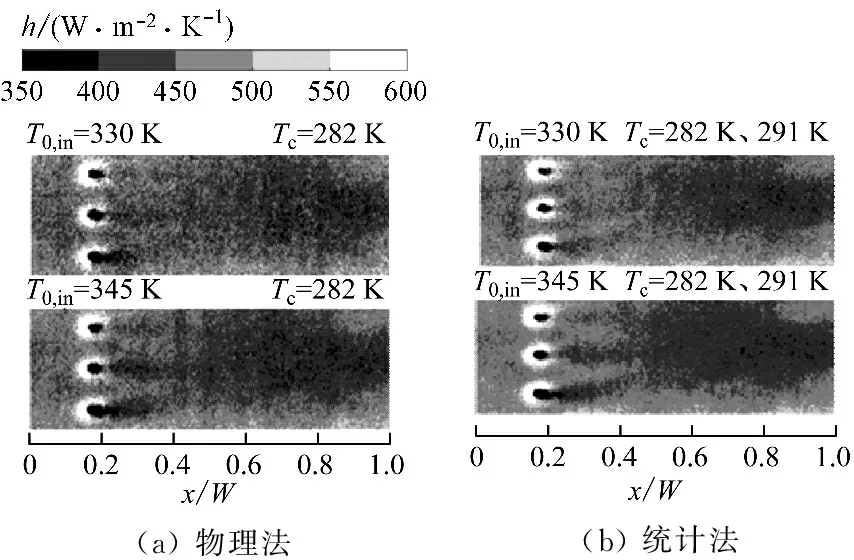
图7 物理法与统计法得到的对流传热系数分布

图8 物理法与统计法获得的沿z方向平均后的对流传热系数分布

3.2 绝热气膜冷却效率

图9 主流总温345 K时物理法与统计法获得的绝热气膜冷却效率分布

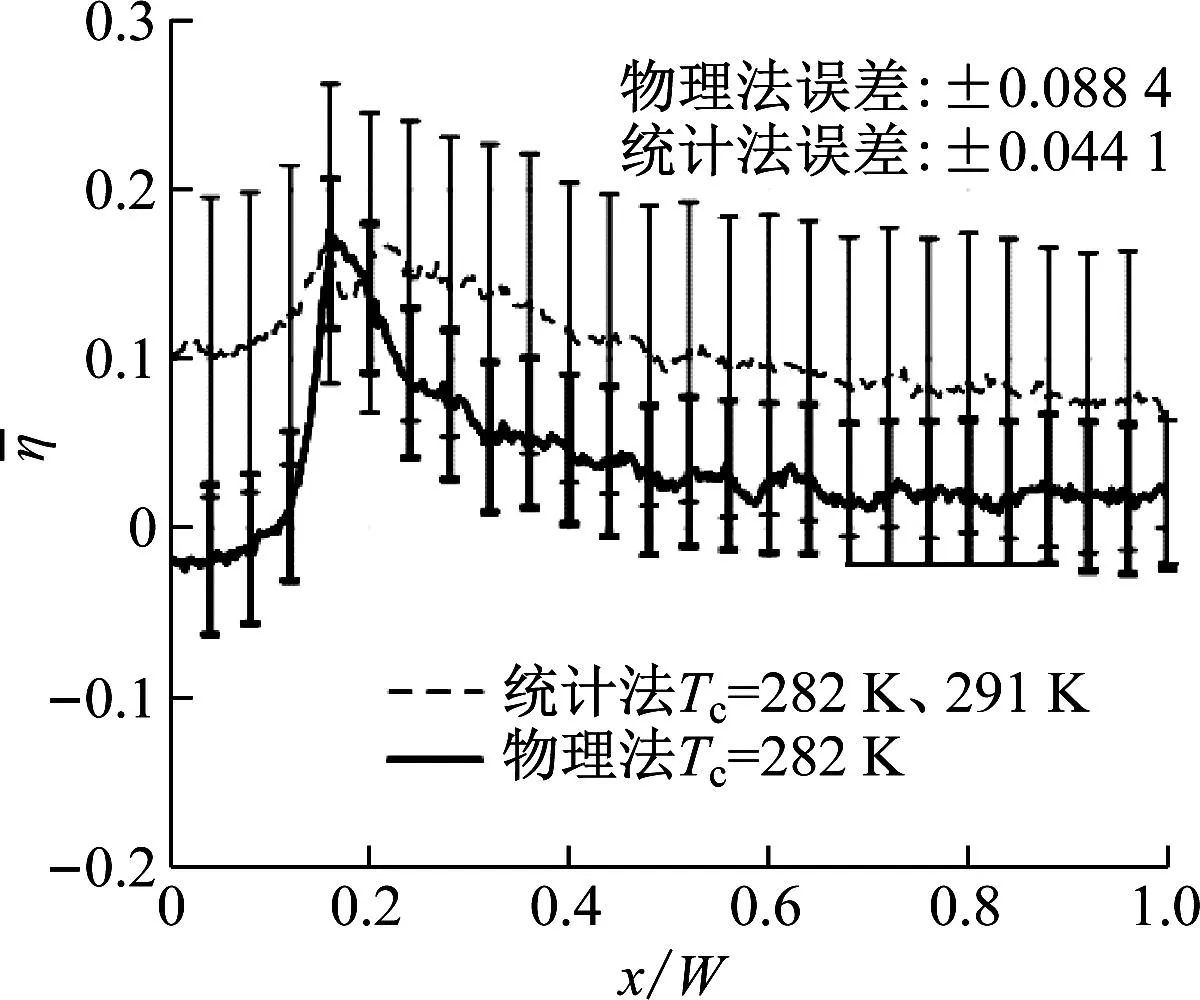
图10 主流总温345 K时物理法与统计法获得的沿z方向平均后的绝热气膜冷却效率及误差分布

图11为物理法获得的沿z方向平均后的绝热气膜冷却效率分布,主流总温为345 K时的绝热气膜冷却效率比主流总温为330 K时高。不同冷气温度下的绝热气膜冷却效率的变化趋势相同。图12为统计法获得的沿z方向平均后的绝热气膜冷却效率分布。与物理法类似,主流总温为345 K时的绝热气膜冷却效率比主流总温为330 K时高。在下游区域,绝热气膜冷却效率受冷气温度影响较小。总体来说,物理法与统计法得到的绝热气膜冷却效率在定性上存在较大的差异,物理法得到的绝热气膜冷却效率变化幅度更大,而统计法得到的绝热气膜冷却效率总体变化较平缓。

图11 物理法获得的沿z方向平均后的绝热气膜冷却效率分布

图12 统计法获得的沿z方向平均后的绝热气膜冷却效率分布

图13给出了主流总温为345 K时物理法与统计法得到的恢复温度分布。因为物理法将恢复温度定义为无冷实验的绝热壁温,所以其恢复温度分布较为平均;而从统计法获得的恢复温度分布中可以观察到气膜孔的位置,表明其恢复温度结果在一定程度上反映了冷气与主流之间的相互作用。2种方法得到的恢复温度之间的根本差别是导致2种方法所得绝热气膜冷却效率定性上存在差别的原因。