用于风功率平抑的SOEC系统功率控制策略

2024-01-01熊星宇

动力工程学报 2023年12期

武鑫, 冯歌, 熊星宇

(华北电力大学能源动力与机械工程学院, 北京 102206)

风力发电作为一种清洁高效的可再生能源,是最有希望替代以化石燃料为基础的能源之一,但因其具有地域性、随机性和间歇性等特点,不能稳定地保持供电,会对电网产生很大冲击。据统计,截至2021年10月底,我国可再生能源发电累计装机容量超10亿kW,其中风电装机容量达到2.99亿kW[1]。风电装机容量的持续上涨导致电网输送不及时,从而导致“弃风”现象出现。风电制氢是一种高效清洁的新能源利用模式,可以有效解决风力就地消纳问题。氢气是连接电能网络与其他能源的桥梁,可以将瞬时的电能转化成长期储存的能源形式。氢能作为一种新的二次能源载体具有能量密度大、来源广、零污染等优点,在航天、军工、建筑等领域都有广泛的应用。目前常用的电解水制氢技术主要有3种,分别是碱性电解 (AEC) 、质子交换膜电解(PEMEC)和固体氧化物电解 (SOEC)。其中,AEC技术最成熟,但存在氢氧气体混合易产生事故的危险;质子交换膜(PEM)电解技术对快速波动的电源适应性强,但造价昂贵;SOEC技术是近年来国内外学者研究的热点,是基于固体氧化物燃料电池(SOFC)的技术,可以看作是SOFC技术的逆运行,具有电解效率高、产氢量大等优点。

目前,国内外SOEC技术研究内容主要侧重于电极、电解质等材料的开发,尚未实现商业化,仍处在实验研究阶段,在电堆建模方面主要依据气体组分、Butler-Volmer 方程、Fick 扩散模型等建立电池状态与电流密度、温度、气量之间的关系[2]。Song等[3]选用一个30层的SOFC电堆,在不同炉温下实验并采集数据,然后选择反向传播(BP)神经网络、支持向量机(SVM)和随机森林(RF)建立电堆预测模型,对不同工况下的电堆输出电压进行预测。Ba等[4]基于替代映射概念建立SOEC电堆模型,并通过30层电堆实验验证了模型参数的正确性。Chandrasekar等[5]建立低温PEM和高温SOEC模型,分析了4种不同可再生能源场景的系统响应特征。Han等[6]采用Elman神经网络(ENN)和改进粒子群算法(MPSO)对固体氧化物电解池进行建模,研究了SOEC在H2O和CO2电解及共电解作用下的稳态效率。Mukelabai等[7]基于热电化学模型,建立可逆固体氧化物燃料电池模型,设计了电力-氨-电力系统。Vialetto等[8]提出采用SOFC/SOEC系统来改造造纸厂发电系统,结果表明该系统在制氢方面具有显著的效益和良好的经济性能。尉倥等[9]将SOEC系统与太阳能耦合,建立了一种采用光伏、光热协同驱动的SOEC高温蒸汽电解制氢系统。钟杰等[10]利用Aspen Plus软件建立3个1 kW固体氧化物燃料电池-热电联供系统模型,研究不同燃料利用率的电堆适用的最佳系统流程。

在风电场接入电力系统并网标准下,针对SOEC的非线性与时滞特性,需要提出一种控制策略来实现功率跟随效果,达到平抑风功率波动的目的,从而实现“弃风”的有效利用。Zhao等[11]提出了一种基于最小二乘支持向量机的超短期功率预测方法,对每个序列构建预测模型,验证了该算法对高波动风电数据的优越预测精度。卢捷等[12]针对风电场输出功率波动较大的问题,建立风氢耦合系统并提出超前控制策略,以最小化功率波动平滑为目标函数,有效减小实际输出与出力计划偏差。针对SOEC电解水制氢技术用于平抑风电场输出功率波动的控制策略研究较少,为了实现SOEC在风电场中的应用,需要在控制策略方面提出较高要求。

针对上述情况,笔者采用SOEC电解水技术,提出一种基于模型预测(MPC)的功率控制策略,以平抑风电场输出功率波动。首先,基于实际数据建立千瓦级SOEC电堆模型并验证了模型精度。然后,针对SOEC系统的非线性和时滞特性,提出一种基于MPC的功率控制策略,用于电解水制氢。接着,基于SOEC系统特性,采用集合经验模态分解方法(EEMD),提出一种风电场输出功率分解方法,获得SOEC系统的充电功率指令。最后,根据某15 MW风电场运行数据,通过仿真验证了提出的SOEC系统控制策略及其平抑风电场输出功率波动的性能。

1 SOEC系统建模

1.1 SOEC系统模型

SOEC系统主要由阴极、阳极和电解质3部分组成,呈“三明治”结构。阴极连接直流电源负极,阳极连接直流电源正极,在电解时阴极侧水蒸气扩散到三相界面,电解生成H2和O2-,O2-通过电解质层到达阳极侧,发生氧化反应,失去电子,生成O2。反应过程如下:

(1)

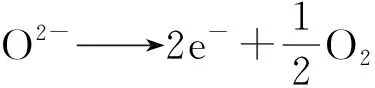
(2)

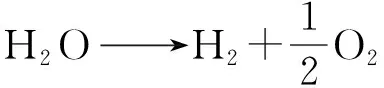
(3)

在实际的电解过程中,由于电荷传输、气体分子传输和材料电阻等因素存在,导致反应偏离平衡状态,产生极化现象。这就导致实际输入的工作电压高于电解水理论电压,且电流越大,损耗也越大。极化现象包括阴极、阳极中发生的浓度过电压ηcon,c、ηcon,a,活化过电压ηact,c、ηact,a以及在电解质和2个电极中发生的欧姆过电压ηohm。电解水反应所需要的实际电压E表示为:

E=Er+ηcon,c+ηcon,a+ηact,c+ηact,a+ηohm

(4)

式中:Er为SOEC开路电压。

根据能斯特方程,SOEC开路电压Er表示为:

(5)

E0=1.253-2.4516×10-4T

(6)

式中:E0为标准电动势,与运行温度T有关;PH2、PO2、PH2O分别为电极中组分氢气、氧气、水蒸气的分压力与标准压力的比值;R为普适气体常数;F为法拉第常数。

浓度过电压主要是由气体分子在多孔电极的传输导致的,多孔性、渗透性、扭曲度和孔径都会影响浓度过电压[13]。采用菲克扩散模型来描述气体运输特性,阴极、阳极浓度过电压分别表示为:

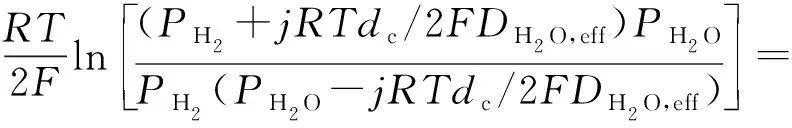
(7)

(8)

式中:j为电流密度;dc和da分别为阴极和阳极的厚度;DH2O,eff、DO2,eff分别为水分子和氧气的有效扩散系数;μ为氧气的动力学黏度;Bg为渗透率。

在缓慢电极动力学主导电化学反应时,活化过电压损失占比较大。根据Butler-Volme方程[14],活化过电压表示为:

(9)

(10)

式中:j0,i为交换电流密度;γi和Eact,i分别为阴极、阳极的指前因子和活化能。

电解质的导电性比连接体和电极的导电性要差,所以欧姆过电压主要与电解质有关,且受电流密度、电解质厚度和运行温度的影响。

(11)

式中:Ld为电解质的厚度。

依据电荷守恒定律求出阴极的产氢率NH2,然后根据电化学反应求出对应的氧气产率NO2,电解水过程中实际消耗的功率Pst以及氢气、氧气摩尔速率(NH2和NO2)分别为:

Pst=Vst·I=(E·N)·(j·ASOEC)

(12)

(13)

(14)

式中:ASOEC为单个电解池的有效面积;N为SOEC电解池数量;Vst为电堆电压;I为电堆电流。

1.2 模型验证

根据数学模型在Matlab仿真平台建立千瓦级SOEC电堆模型,如图1所示。

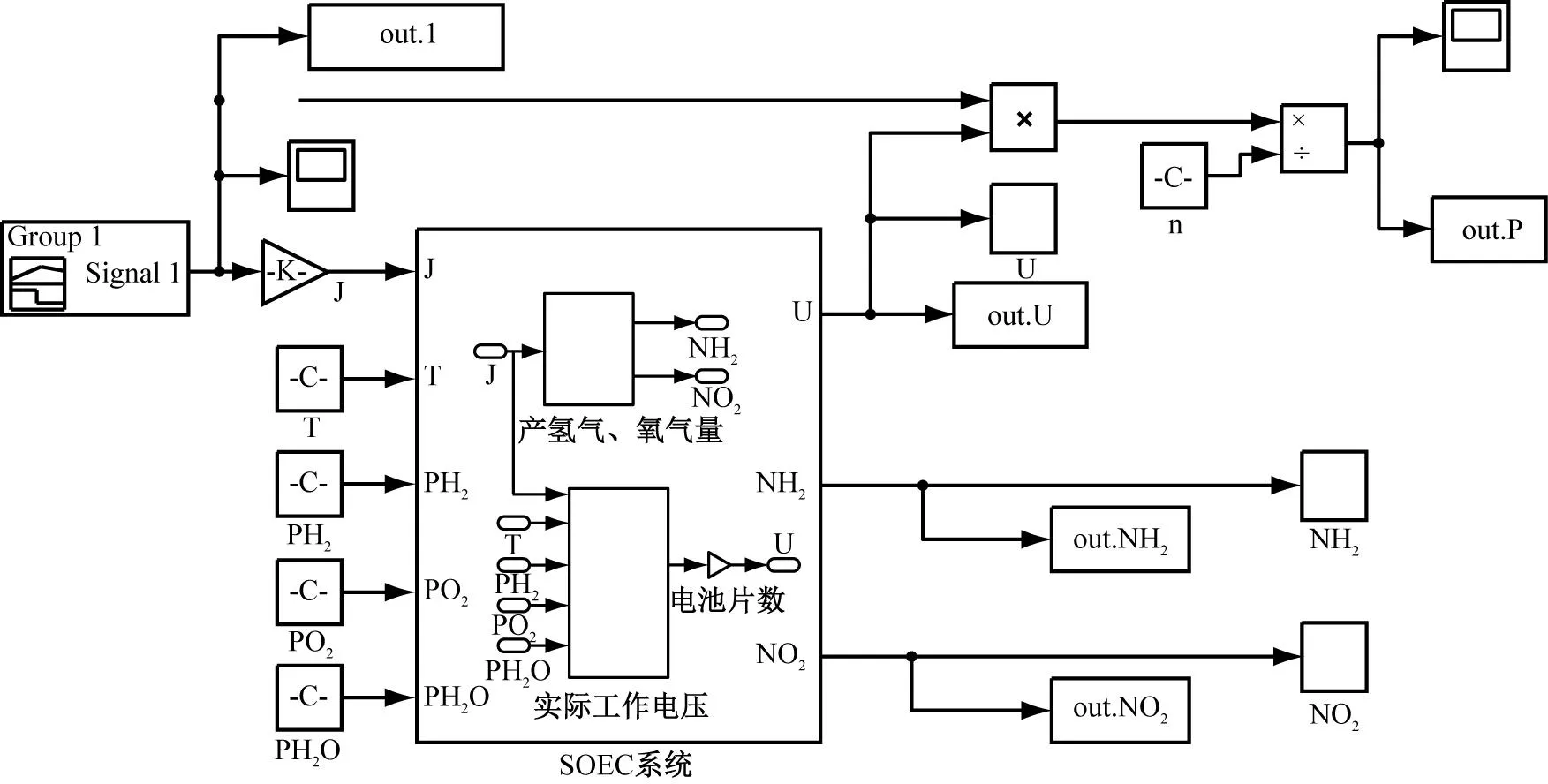
图1 SOEC电堆模型

将表1中实验设定的操作条件和选用的电解池结构参数代入建立的SOEC电堆模型中进行仿真。

表1 电解池结构尺寸参数和主要的操作条件

在700 ℃时,某层单电解池电压的实验值和模拟值如表2所示,计算相对误差并选取平均绝对误差(eMAE)、均方根误差(eRMSE)和平均绝对百分比误差(eMAPE)作为评价指标。具体计算公式如下:

(15)

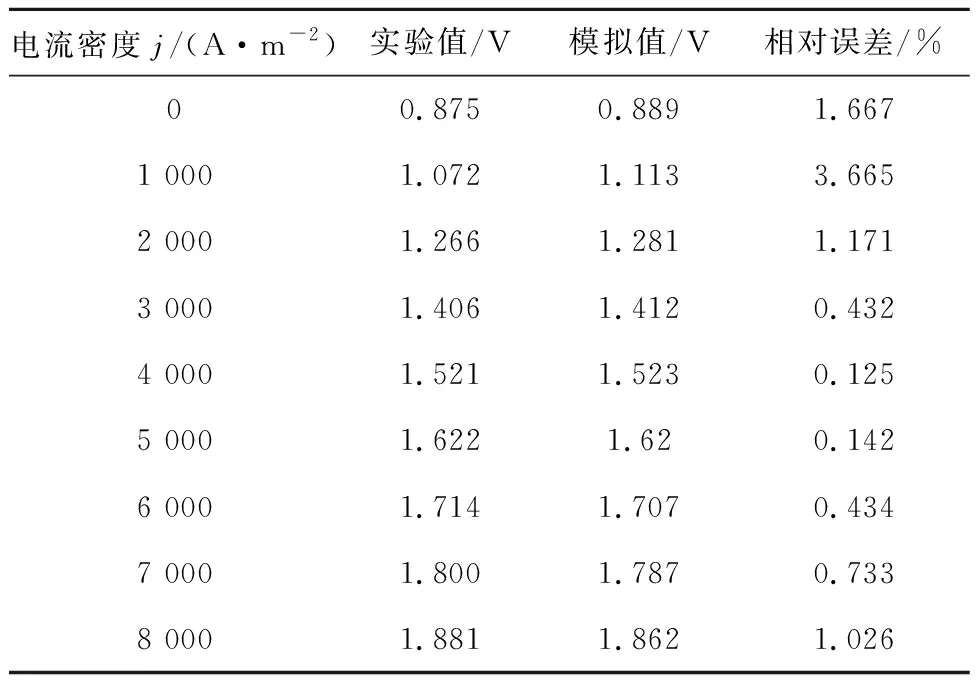
表2 单电解池电压模拟数据与实际数据的相对误差

(16)

(17)

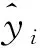
eMAE可反映预测误差的实际情况,eRMSE可反映模型的鲁棒性及其控制绝对误差的能力。两者较小的统计测量值对应于模型较好的预测能力,当其数值接近0时,表示模型输出与实际输出吻合。本模型中eRMSE为0.018 5,eMAE为0.015,表明模型具有较好的预测能力。eMAPE为1.043 8%,反映了模型预测结果的准确性。图2为某单层电解池的电流密度与电压特性,发现模拟数据与实验数据吻合,验证了单电解池模型的高精度,从而可以验证30层的千瓦级SOEC电堆模型的精度和准确性。

图2 单电解池电压模拟数据与实验数据的对比

2 SOEC系统功率控制策略

2.1 基于MPC的SOEC系统功率控制策略

SOEC系统在开环状态下存在非线性和时滞特性,在控制系统中时滞性对控制效果有着非常不利的影响,需要调节输入功率来实现SOEC电堆高效、稳定运行,因此提出一种基于MPC的功率控制策略。靳方圆等[15]以SOFC输出稳定电压为目标,设计了一种基于改进支持向量机(SVM)的非线性预测模型,并利用人工蜂群 (ABC) 算法优化支持向量机参数,并证明了ABC-SVM模型可以很好地跟踪电压设定值。本文采用精确预测模型来改进传统Smith预估控制,利用贝叶斯优化(BOA)来改进支持向量机,从而通过训练得到精确的SOEC模型,并采用高斯核函数解决数据中存在的内积问题,即实现预估模型与实际被控对象匹配,最大限度改善时滞现象。

2.1.1 SVM原理

SVM的基本原理是通过某个核函数将输入样本变化投影到高维空间,然后在该高维空间求出最优分类超平面。SVM方法步骤如下:

(1) 存在训练集P={(x1,y1),…,(xi,yi),(xn,yn)},其中xi为输入向量,yi∈(-1,+1)为类标签。

(2) 设定最优超平面为wTx+b=0,其中w为权值向量,b为偏置向量,x为最优超平面时的样本输入向量。

(3) 根据结构风险最小化原理将超平面求解问题转为二次规划约束优化问题。

(18)

式中:C为惩罚因子,用于权衡模型复杂性;εi为松弛变量。

(4) 引入拉格朗日乘子,将式(18)转化为对偶问题来求解,SVM分类器的表达式f(x)为

(19)

式中:ai为拉氏乘子;φ(xi,x)为核函数。

基于实际数据建立千瓦级SOEC电堆模型,在消耗功率为0～1 000 W范围内,输入变量为斜坡信号,共收集1 130个电流、功率信号作为输入、输出数据。在开展模型训练时,交叉验证折数为10,核函数为高斯核,核尺度为1,优化器选用贝叶斯优化。

SVR模型训练的预测功率和真实功率如图3所示。本模型中eRMSE为0.390 39,eMAE为0.339 42,训练时间为162.68 s,eRMSE和eMAE接近0,表明该模型具有较好的预测能力,说明利用改进支持向量机训练得到的SOEC模型精确度很高。

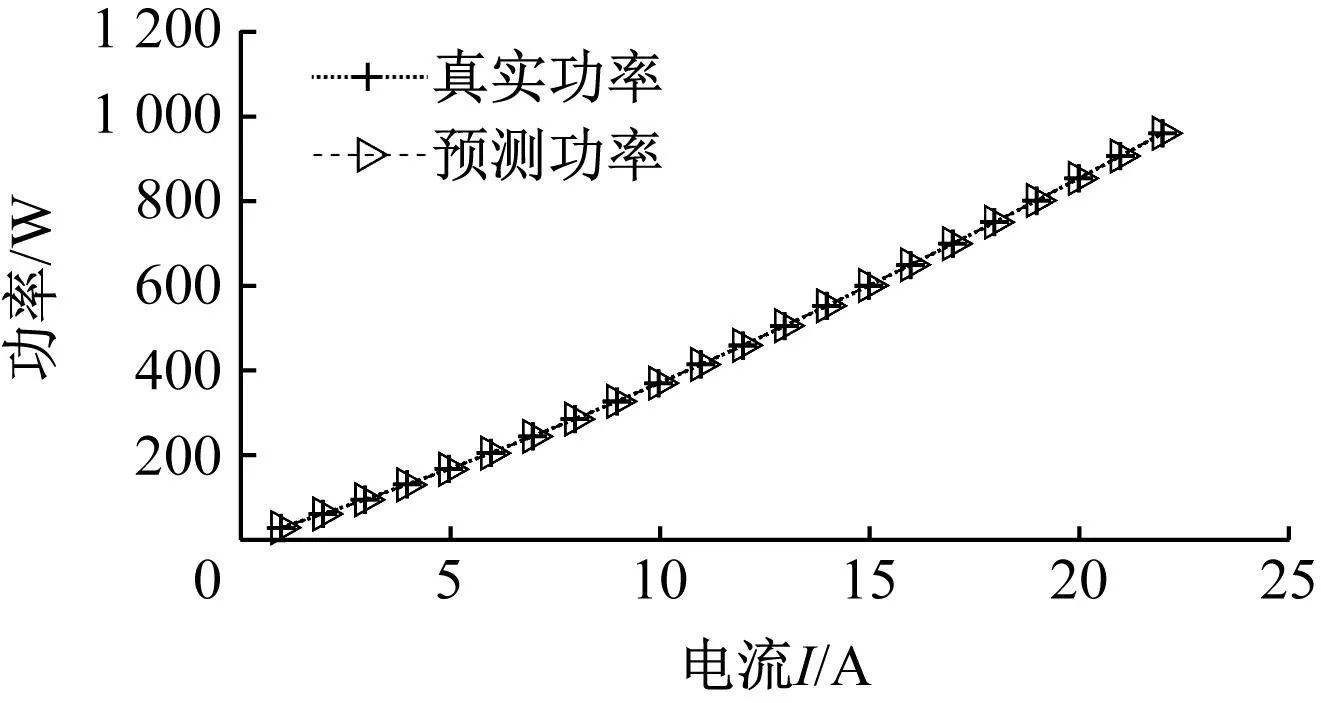
图3 SVR模型训练结果

2.1.2 基于MPC的功率控制策略

比例积分(PI)控制器具有稳定性高和结构简单等优点。常规PI控制器在遇到非线性和时滞环节会出现闭环稳定性差等问题。因为SOEC系统具有非线性和时滞特性,若只采用PI控制器或Smith控制器很难实现预期效果。针对上述情况,Kim等[16]针对遥控机器人系统的输入和反馈时滞问题,提出了对遥控系统时滞效应的补偿措施,对Smith预测器结构进行改进,利用递归神经网络代替线性估计器,结果表明该方案控制效果更好。笔者基于Smith预估器原理以及SOEC系统的非线性和时滞特性,利用SVM训练的SOEC模型来预测无延时部分功率消耗情况,提出了一种基于MPC的功率控制策略[17],具体原理如图4所示。预测模型为基于SVM方法建立的SOEC系统模型,其中e-τs为本系统时间延迟环节;R(s)为目标值;Cs(s)为系统反馈补偿值;e(s)为误差;h(s)为SOEC系统的输入值;C(s)为系统输出值。

图4 基于MPC的SOEC功率控制策略框图

当电流经过预测模型后得到无延迟部分的预测消耗功率P0,进而得到Smith预估器P0(1-e-τs),当电流经过SOEC系统后得到无延迟部分的消耗功率P1,则被控对象SOEC系统可以表示为P1e-τs,当P0=P1时,延迟部分e-τs被消除,因此Smith预估器可以完全消除系统中存在的纯滞后现象。当输入参考功率R(s),即利用EEMD分解之后得到充电功率指令,PI控制器通过调节控制输入SOEC系统的电流h(s),经过SOEC系统得出电解水实际电压,根据式(12)可以得到电解水过程实际消耗的功率,经过反馈补偿调节使误差趋近于0,从而实现功率控制。

本文采用PI控制器,利用PID Tuner工具箱进行参数整定,初步得到一组较为理想的控制参数Kp和Ki,在此基础上结合传统经验法并按照Kp、Ki的顺序反复调试优化,最终得到PI控制器最理想的参数,使控制系统达到稳定。

2.2 基于EEMD的风电场输出功率分解方法

EEMD方法的本质是一种叠加高斯白噪音的多次经验模式分解,其通过高斯白噪音频率均匀分布的统计特性,通过每次加入同等幅值的不同白噪音来改变信号的极值点特性,之后进行多次经验模态分解(EMD)得到相应固有模式函数(IMF)分量,进行总体平均来抵消加入的白噪音,从而有效抑制模态混叠的产生。EEMD方法步骤如下:

(1) 设定总体平均次数Z。

(2) 将具有标准正态分布的白噪音ni(t) 加到原始信号x(t)上,产生一个新的信号xi(t)=x(t)+ni(t)。

(3) 对所得含噪音的信号xi(t)分别进行EMD分解,得到各自IMF和的形式:

(20)

式中:ci,j(t)为第i次加入白噪音后分解得到的第j个IMF分量;ri,j(t)为残余函数,代表信号的平均趋势;J为IMF的数量。

(4) 重复步骤(2)和步骤(3)Z次,每次分解加入幅值不同的白噪音信号,得到IMF的集合为{c1,j(t),c2,j(t),…,cZ,j(t)}。

利用不相关系数序列的统计平均值为0的原理,将上述对应的IMF进行集合平均运算,得到EEMD分解后的最终IMF,即;

(21)

式中:cj(t)为EEMD分解的第j个IMF;i=1,2,…,Z;j=1,2,…,J。

采用EEMD方法处理风电场输出功率后,会得到频率由高到低排列的IMF分量以及残余分量,根据风电并网波动量限制要求,对高、低频功率进行调整重构,将符合风电并网要求的低频分量进行并网,将高频分量分配给储能系统[18]。以储能系统不能超过风电装机容量的20%为约束条件,将高频分量部分进行分配、次高频部分进行处理,进而得到SOEC系统充电功率指令。

3 实例验证

3.1 基于MPC的SOEC功率控制方法特性

随着风力发电的不断发展,风电输出功率的随机性和波动性使电能质量下降,电网调频难度加大。沈小军等[19]提出一种基于轮值思想的碱性电解槽阵列协调控制策略,并通过实例仿真证明在不同功率情况下,电解槽阵列可以很好地跟随风功率曲线,从而实现平抑风功率波动和氢能源的绿色获取。调峰调频的本质是风功率的变化,故在独立的SOEC模型基础上提出了基于MPC的功率控制策略,以实现风功率波动的平抑。

假设SOEC系统具有足够的储氢、储氧装置,同时保证充足的水蒸气供应,当将充电功率指令输入至SOEC系统时可持续工作,故暂未考虑该系统的荷电状态和储能电量限制。SOEC系统扩展性较强,可由多个电池堆组装而成,额定功率从数瓦到数千瓦不等,可根据不同需求进行灵活调整。所建千瓦级SOEC系统的输入功率可在0～1 000 W之间变化。

如图5所示,当SOEC系统输入参考功率为1 000 W时,通过调节PI控制器,SOEC系统可以快速准确地跟随参考功率信号并稳定到新的参考值,且响应时间为9.605 s,稳态时间为14.41 s,说明该系统具有良好的功率控制能力,可以满足平抑风电场功率波动的需求。

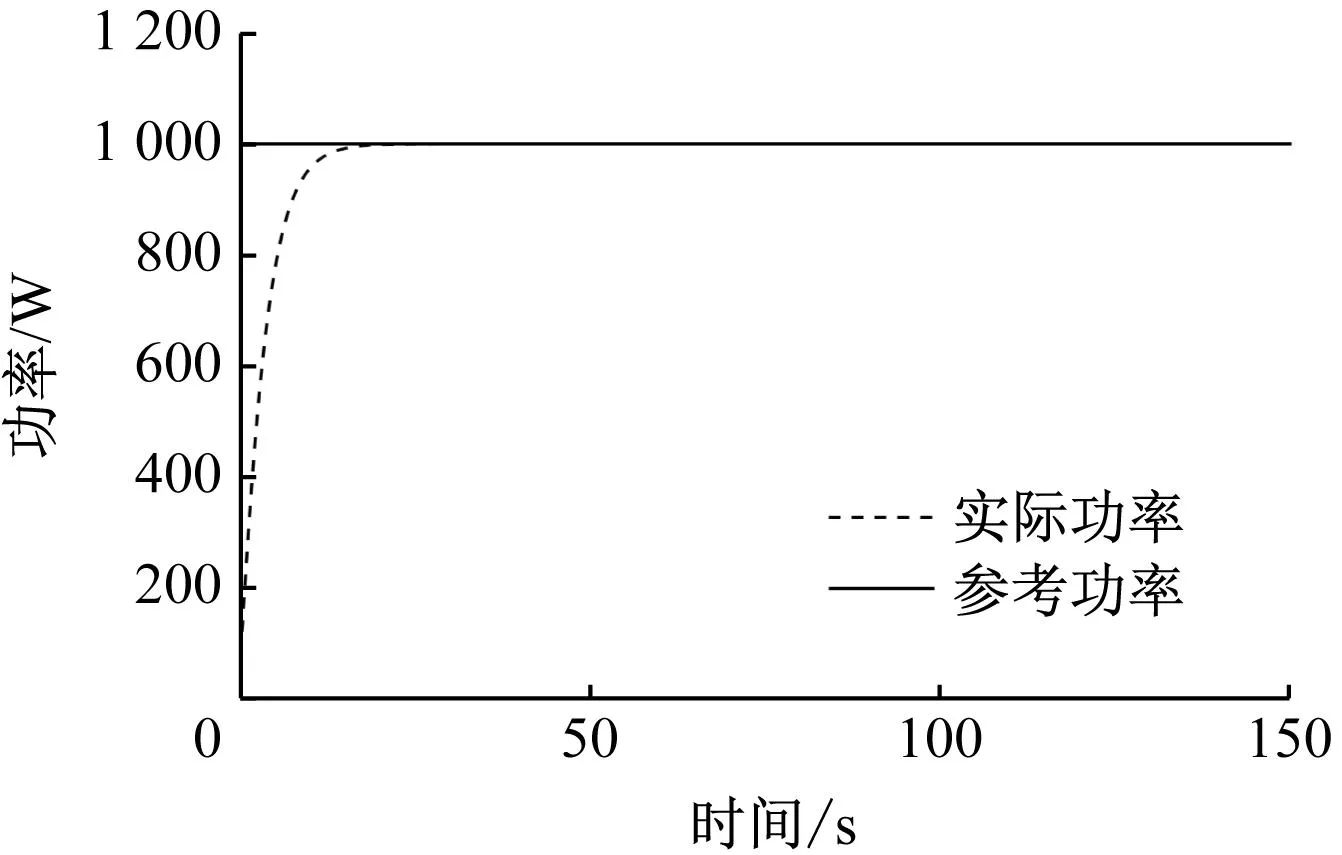
图5 SOEC系统功率控制特性

3.2 SOEC系统功率指令

采用某15 MW风电场实际运行数据,采样时间30 s,共采集480个数据点,风功率原始数据如图6所示,输出功率最大和最小分别为15.22 MW和1.86 MW。

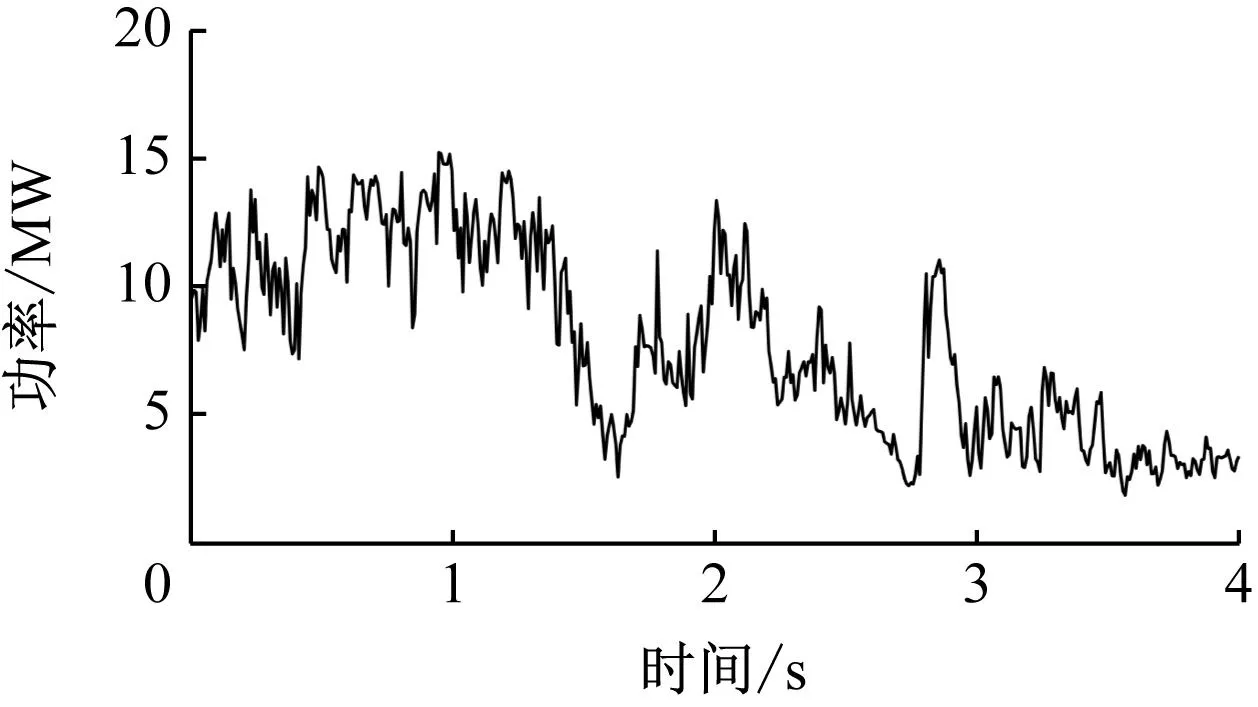
图6 风电场输出功率

根据GB/T 19963.1—2021《风电场接入电力系统技术规定》的细则,当风电场装机容量小于30 MW时,风电场1 min有功功率最大波动量应不超过临界线3 MW,才可满足风电场接入电力系统的标准并网要求。在1 min窗口长度内,定义最大功率Pmax与最小功率Pmin的差值为波动量Fp。

如图7所示,1 min中最大波动量为5.603 MW,最小波动量为0.016 7 MW,可见,原始风电场输出功率明显不满足并网标准,需要引入SOEC系统来平抑输出功率波动。采用EEMD方法处理风电场输出功率,得到各IMF分量的相关系数如表3所示。

表3 采用EEMD方法得到的IMF分量相关系数

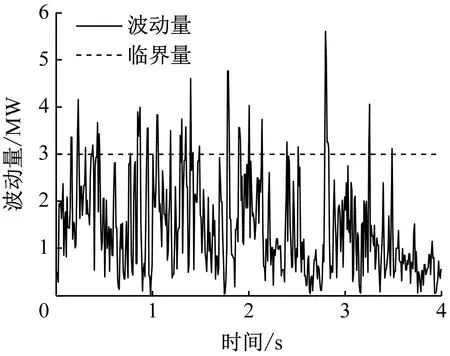
图7 1 min最大波动量

IMF1～IMF6信号依次由高频到低频变化,根据风电并网标准,利用信号重构将符合风电并网最大波动量要求的低频分量IMF2、IMF4～IMF6和余量R(重构简化为IMF2456R)进行并网,如图8所示。其中,IMF23456R表示用于获取并网和SOEC指令的参考功率,IMF2456R表示并网功率。

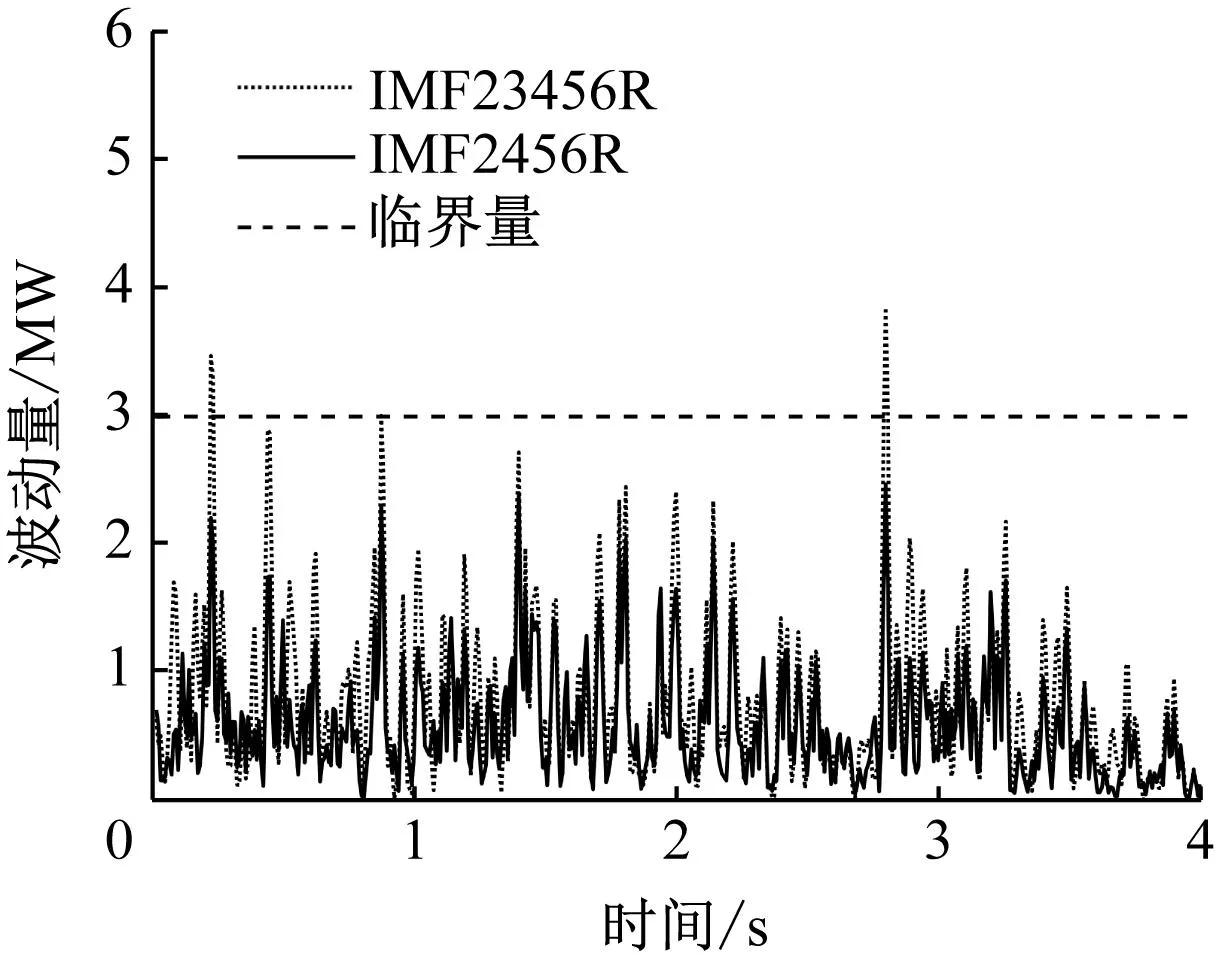
图8 信号重构后1 min最大波动量

根据频率特性,高频分量IMF1可采用功率型储能系统,如飞轮、超级电容等储能系统进行平抑,而次高频分量IMF3信号作为总充放电指令,如图9所示。以储能配置不超过风电场装机容量的20%为约束条件,符合储能配置要求。IMF3信号中正值部分作为充电功率指令被分配给SOEC系统进行平抑处理,负值部分作为放电功率指令需要SOFC系统进行处理,故只考虑充电功率指令,放电功率指令将在后续工作中研究。

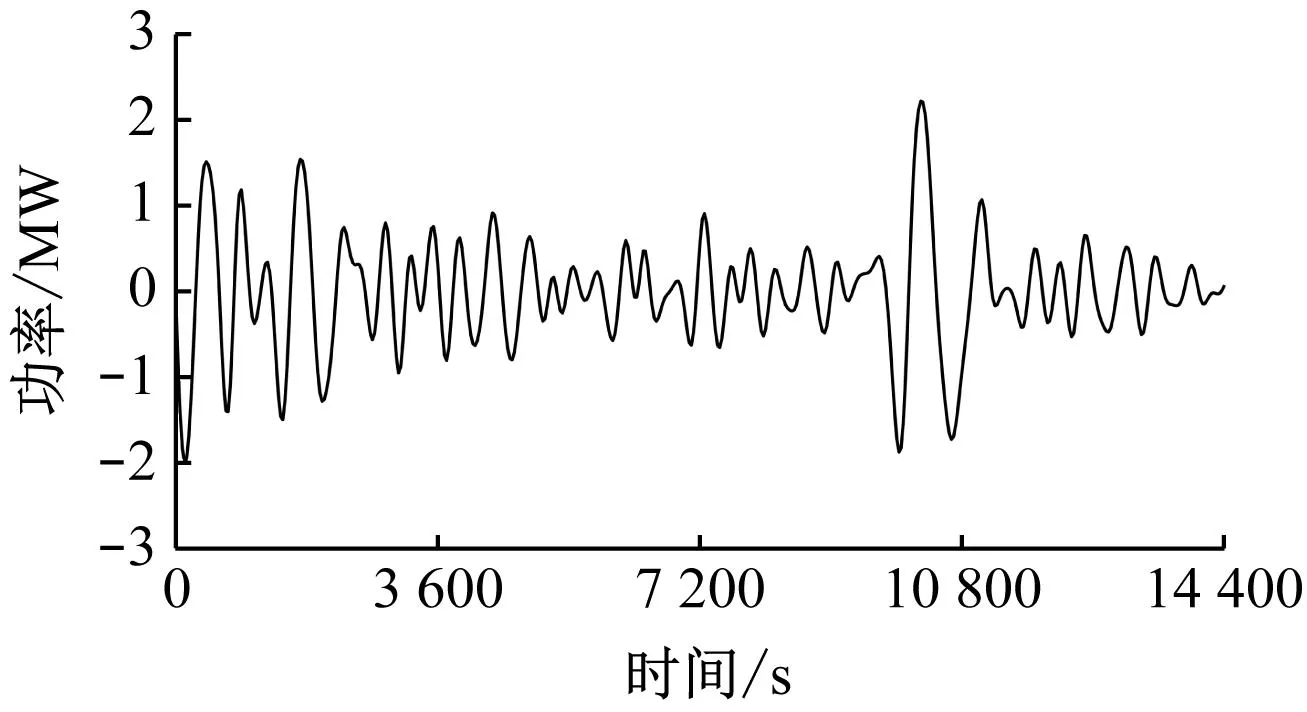
图9 总充放电指令

IMF3信号经过处理才可分配给SOEC系统进行平抑处理,基于IMF3信号提取正值部分得到充电功率指令,由于单组千瓦级SOEC系统容量为1 kW,故需要2.5 MW的SOEC阵列来平抑风功率波动,即2 500组千瓦级SOEC系统并联工作。对于每组千瓦级SOEC系统,充电功率指令的时间间隔为60 s,变化范围为0～1 000 W,如图10所示。

图10 SOEC系统充电功率指令

3.3 SOEC系统功率控制策略和制氢性能

将充电功率指令代入SOEC系统中运行时功率控制情况如图11所示。随机选取5个时间点的充电功率指令和模拟功率数据,并计算相对误差,如表4所示,其中最大相对误差为3.039%,最小相对误差为0.603%,且eMAPE为1.674%,说明SOEC系统具有很好的功率控制效果,从而可以有效平抑风电场输出功率波动。

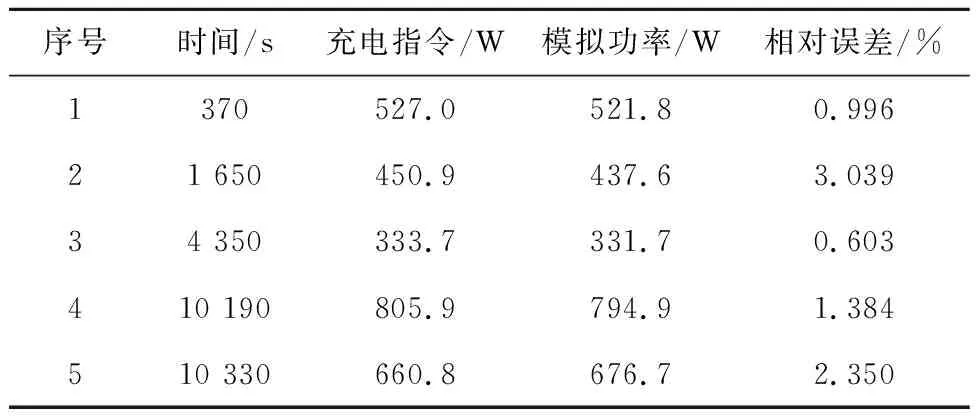
表4 SOEC系统充电功率的控制误差

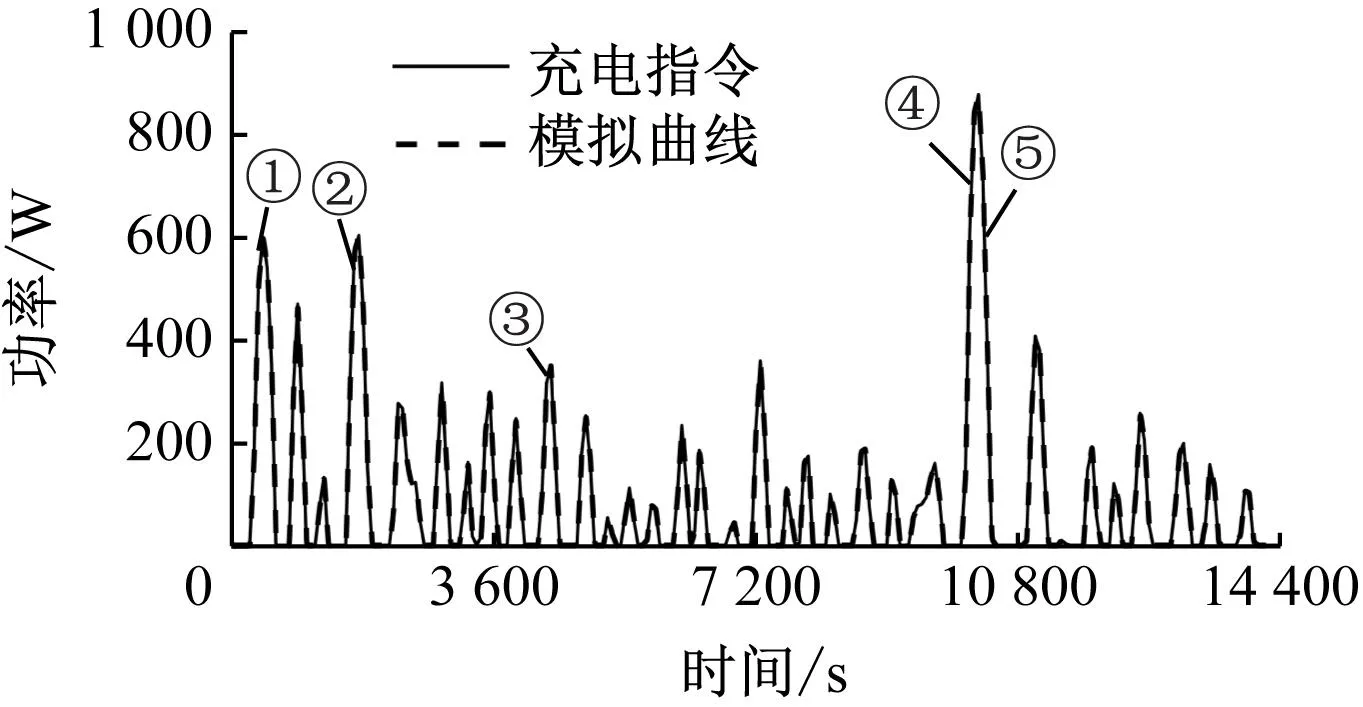
图11 SOEC系统充电功率控制情况

氢气产量如图12所示,在10 260 s时单秒产氢量最大,为3.18×10-3mol,即6.36×10-3g。4 h内SOEC电解水系统工作33次,总工作时间为118 min,氢气总产量为5.55 mol,即11.1 g。

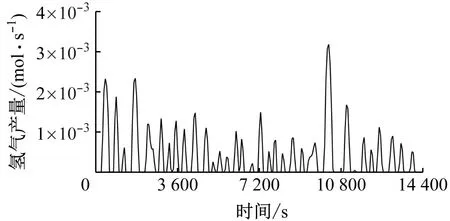
图12 氢气产量变化

氧气产量如图13所示,在10 260 s时单秒产氧量最大为1.59×10-3mol,即0.050 9 g。4 h内SOEC电解水系统工作33次,总工作时间为118 min,氧气总产量为2.775 mol,即88.8 g。

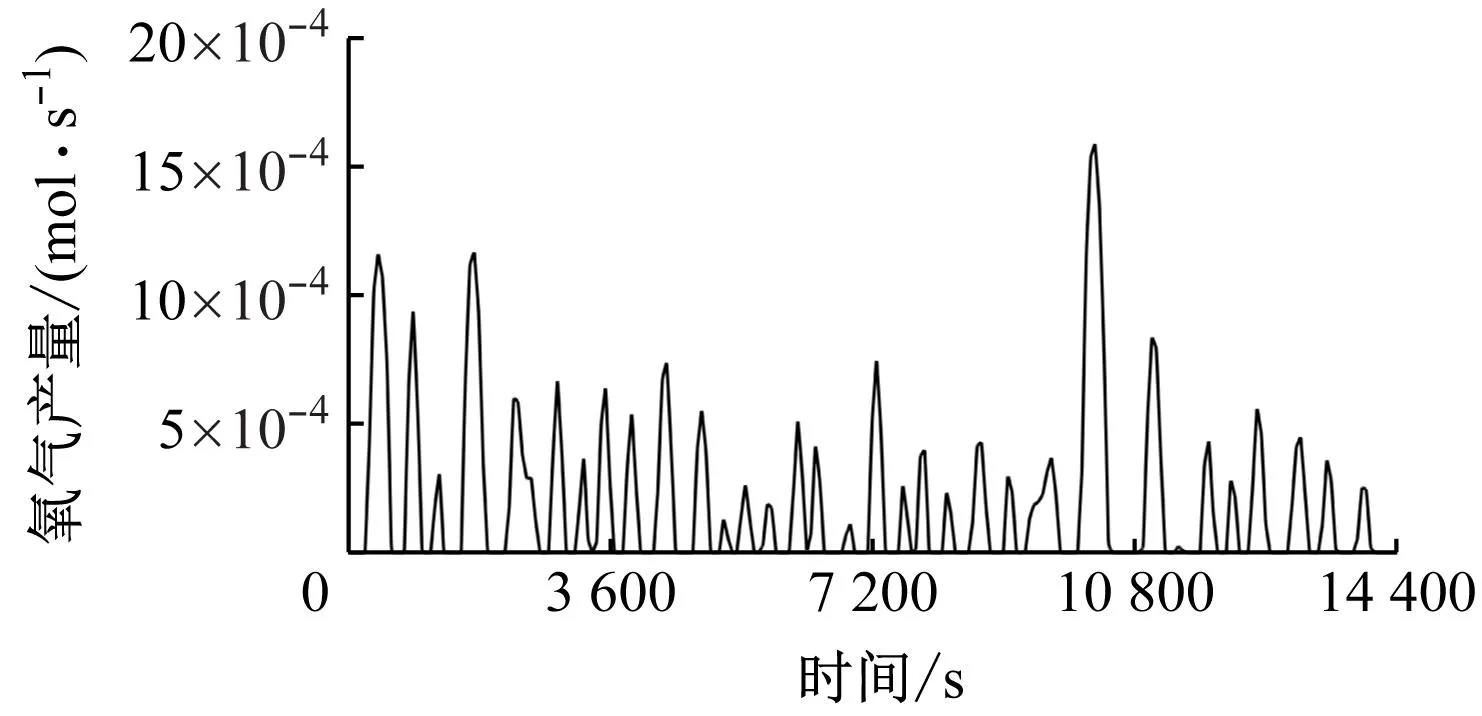
图13 氧气产量变化

上述为单组SOEC系统工作情况,2 500组1 000 W的SOEC系统并联进行工作,在4 h内氢气总产量为27 750 g,氧气总产量为222 000 g。对比图11～图13可以发现,氢气产量、氧气产量与SOEC系统三者的充电功率指令变化趋势一致,表明SOEC电解水制氢系统的准确性和控制策略的有效性,该系统可平抑风电输出功率的波动。