湍流普朗特数模型对水平圆管内sCO2传热预测的影响
2024-01-01谢雄州叶道铭黄俊辉王建勇
谢雄州, 叶道铭, 黄俊辉, 王建勇
(中山大学·深圳 航空航天学院,深圳 518107)
超临界二氧化碳(supercritical carbon dioxide, sCO2)是一种在动力循环和能量转换中能显著提高热效率的工质[1],在动力工程领域有着广阔的应用前景[2-3]。不同于一般的常物性流体,sCO2的热物理性质在拟临界点附近会发生剧烈变化。由于物理性质的剧烈变化而诱发的浮升力或热加速效应导致流场和温度场之间强烈耦合,从而影响流场和湍流结构[4-5],表现为传热强化(HTE)和传热恶化(HTD)等异常传热现象。传热恶化的发生会导致传热系数降低,局部壁面温度急剧升高,传热效率降低,并对超临界换热装置的安全、稳定运行带来严峻挑战。因此,深刻且准确了解sCO2湍流流动传热行为对于相关超临界流体换热部件的设计及研发至关重要。
为了可靠地预测超临界流体的流动传热特性,学者们尝试了各种不同的数值方法和模型。Reynolds Average Navier-Stokes(RANS)湍流模型在计算精度与成本之间达到了较好的平衡,因此在工程中得到广泛应用,但传热恶化时其对超临界换热的预测性能通常较差。对于RANS湍流模型,湍流普朗特数Prt是一个重要参数,且通常设定为定常值(Prt=0.85)。此举对常物性流体而言,其合理性得到普遍接受,但对于物性变化剧烈的超临界流体,其适用性遭到广泛质疑。因此,一些学者尝试提出湍流普朗特数修正模型以改善RANS湍流模型对超临界湍流传热的预测能力。Bae[6]基于混合长度理论提出了变Prt模型,并将其应用于多种超临界工质在竖直管内的湍流传热计算中,结果显示修正模型的计算结果与实验数据吻合良好。Tang等[7]在Kays[8]的总结推导上,基于SSTk-ω模型提出了分段函数式的变Prt模型;Du等[9]又在此模型基础上进一步引入压力修正因子和管径修正因子,形成了适用性更广的变模型。此外,还有众多研究者(Tian等[10]、Kong等[11])提出了一系列变湍流普朗特数模型。然而,上述变Prt模型的提出背景及修正应用均是面向竖直超临界管流的。水平布局同样在超临界换热设备中被广泛采用,但不同于竖直管道换热所呈现的周向均匀性,水平换热过程中密度不同的sCO2受浮升力的驱使会产生显著的流体分层现象,继而导致巨大的上、下壁温差。而RANS湍流模型应用于水平管道超临界传热计算时同样存在较大偏差,此情形下湍流普朗特数的适用性及其对计算可信度的影响有待进一步剖析,同时在竖直管流动预测上卓有成效且普适性较好的变Prt修正模型应用于水平超临界流动传热的预测亦值得尝试。
鉴于此,笔者分析了定常湍流普朗特数(Prt=0.85)在强、弱2种浮升力效应下对水平sCO2湍流传热的预测性能,而后引入现有典型的Prt修正模型进行数值模拟,并将模拟结果与实验数据进行详细对比,以探究传热预测的可靠性,并系统分析Prt及其相关修正模型对水平sCO2流动传热计算的影响。研究成果对水平超临界湍流传热RANS湍流模型模拟及其深层修正理论具有重要意义。
1 物理模型与数值方法
1.1 几何模型
本文开展数值模拟时所采用的物理模型如图1所示,图中:g为重力加速度;din为圆管内径;φ为圆管周向角;L1、L2和L3分别表示圆管发展段、加热段和缓冲段的长度。该模型的几何尺寸与Theologou等[12]和Adebiyi等[13]的实验圆管参数相同,其针对水平sCO2的湍流传热进行了宽工况范围下系统而细致的测量,具体参数见表1。加热段前、后分别设置了绝热段以降低进、出口效应。圆管周向角度φ为0°、90°(270°)和180°的位置分别对应圆管的顶母线、中母线和底母线。
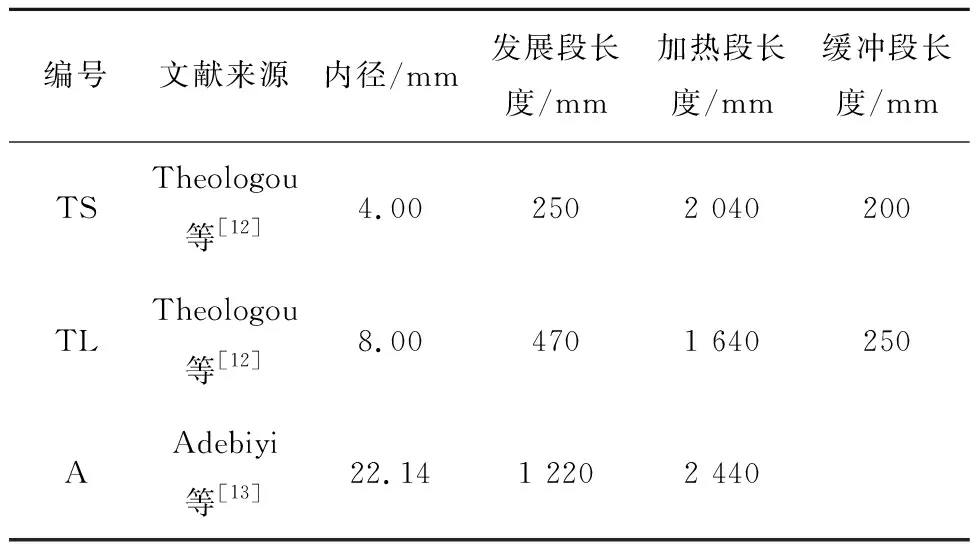
表1 计算模型几何参数

图1 物理模型
1.2 控制方程
采用ANSYS Fluent 19.2软件求解器开展模拟计算,笛卡尔坐标系下连续性方程、动量方程、能量方程的稳态形式分别如式(1)~式(3)所示。
连续性方程:
(1)
动量方程:
(2)
能量方程:
(3)
SSTk-ω模型由于近壁区域作了低雷诺数处理,可以满足边界层高精度的模拟需求,其在超临界流体传热计算中表现出色,受到众多研究者的青睐[14-15],因此也被选用至本文所探究的sCO2水平流动传热模拟中。SSTk-ω模型中湍流控制方程如下:
湍动能k输运方程:
(4)
比耗散率ω输运方程:
(5)
式中:Γk为湍动能k的有效扩散系数;Γω为比耗散率ω的有效扩散系数;Gk为湍动能生成项;Gω为耗散率生成项;Yk为湍动能耗散项;Yω为比耗散率ω的耗散项;Dω为交叉扩散项;Sk为湍动能k的自定义源项;Sω为比耗散率ω的自定义源项。
更多模型细节可参考文献[16]。
1.3 典型湍流普朗特数修正模型
现有Prt修正模型大多面向竖直管内超临界流动传热计算,且主要分为2类:第一类基于竖直管内超临界湍流传热状态,依靠相关理论推导及无量纲分析而得出,如Bae[6]基于混合长度理论提出的变Prt修正模型;第二类主要基于管内超临界湍流传热特征,对流动进行分层(尤其是边界层内)继而相应合理赋值湍流普朗特数。第一类湍流普朗特数修正模型的提出背景及依据与水平流动情形明显不同,故不能直接应用。因此,本文引入并测试第二类Prt修正模型针对水平sCO2湍流传热的计算预测。
此处选取普适性较好的Tang等[7]和Du等[9]提出的变Prt修正模型。其中,Tang等[7]提出的模型描述为:
(6)
式中:A为可调节的常数,Tang等[7]推荐A取值为15。
而Du等[9]提出的模型为:
(7)
式中:fd、α1、α2均为管径修正因子,fd=6.2(din-4)0.24,α1=0.24din-0.7,α2=0.05din-0.07;fp为压力修正因子,fp=[1+0.019(p/pcr)29],pcr为临界压力。
为方便叙述,Du等[9]、Tang等[7]提出的模型在后文分别称为Du模型和Tang模型。
1.4 网格划分与无关性验证
流体计算域网格由ANSYS ICEM软件生成,采用结构化六面体网格,圆管横截面采用O形网格划分。由于黏性底层和缓冲层的网格质量对SSTk-ω低雷诺数湍流模型求解近壁处流动传热细节至关重要,因此在近壁面处对网格进行局部加密,划分的网格横截面如图2所示。
图2 计算域横截面网格
为检验计算网格的独立性,分别对内径为4 mm、8 mm和22.14 mm的水平圆管进行网格无关性验证。以内径为4 mm的水平圆管为例,在保持第一层网格无量纲高度y+<1的情况下,对流体域近壁面处网格进行不同程度的加密处理,分别得到84.4万、115.8万、280.6万和445.3万等4种不同密度的计算网格。这些网格在质量流量G=800 kg/(m2·s)、均匀加热热流密度q=30 kW/m2、入口温度Tin=30 K的工况下计算得到的加热壁面平均温度Tw随轴线位置的变化分布如图3所示。由图3可以看出,当网格数大于280.6万时,加热壁面平均温度随网格数增加已无明显变化。为节省计算成本,4 mm水平圆管的计算网格数选定为280.6万。同理,分别对内径为8 mm和22.14 mm水平圆管的计算模型进行网格独立性分析,选用网格数分别为360.4万和437.6万。
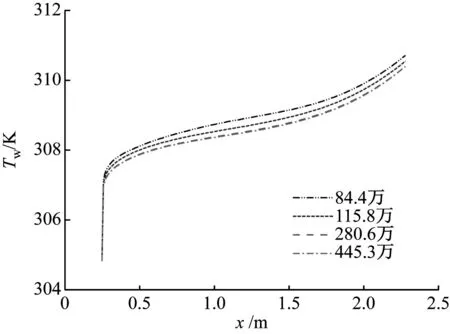
图3 网格独立性验证
1.5 边界条件与计算方法
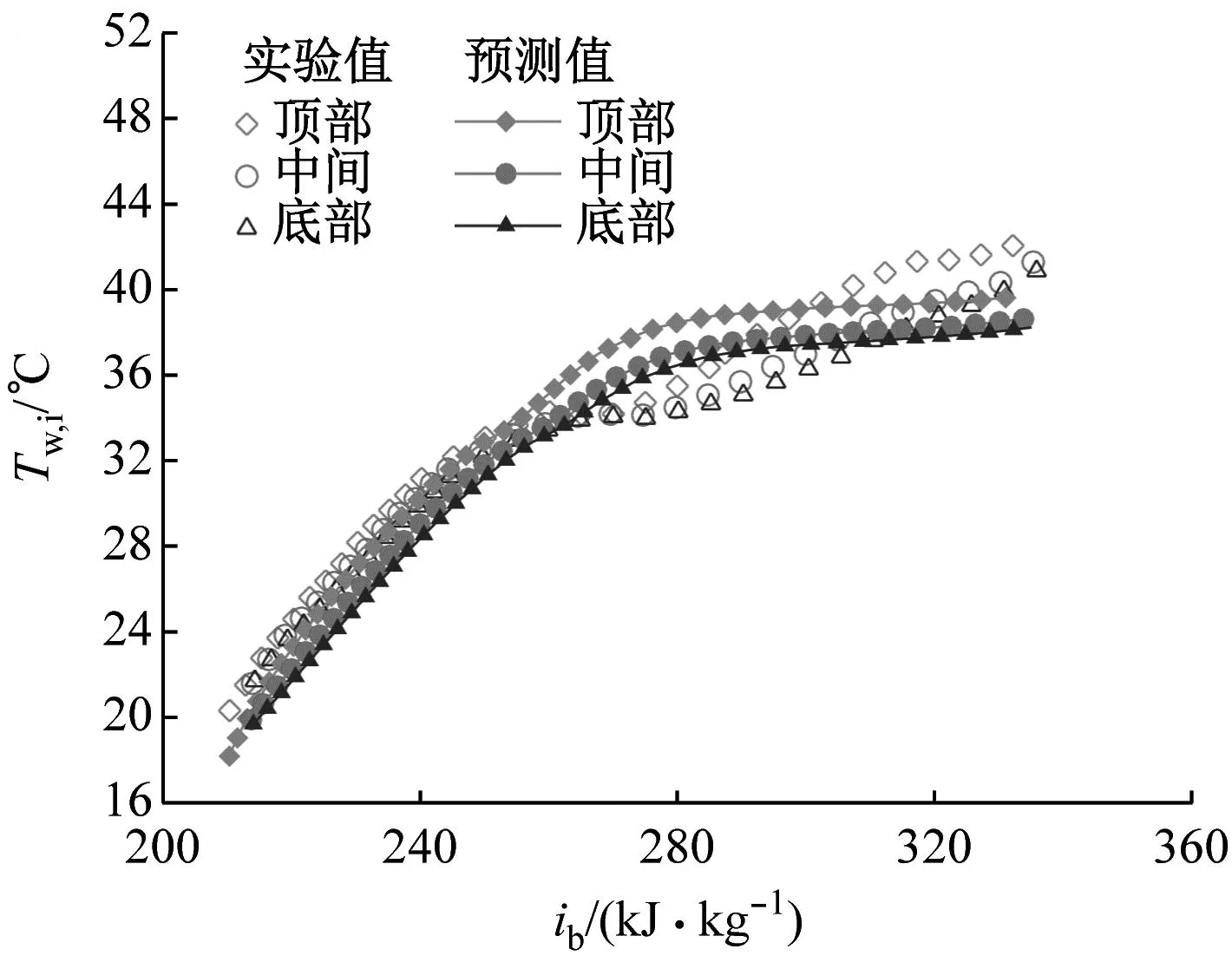
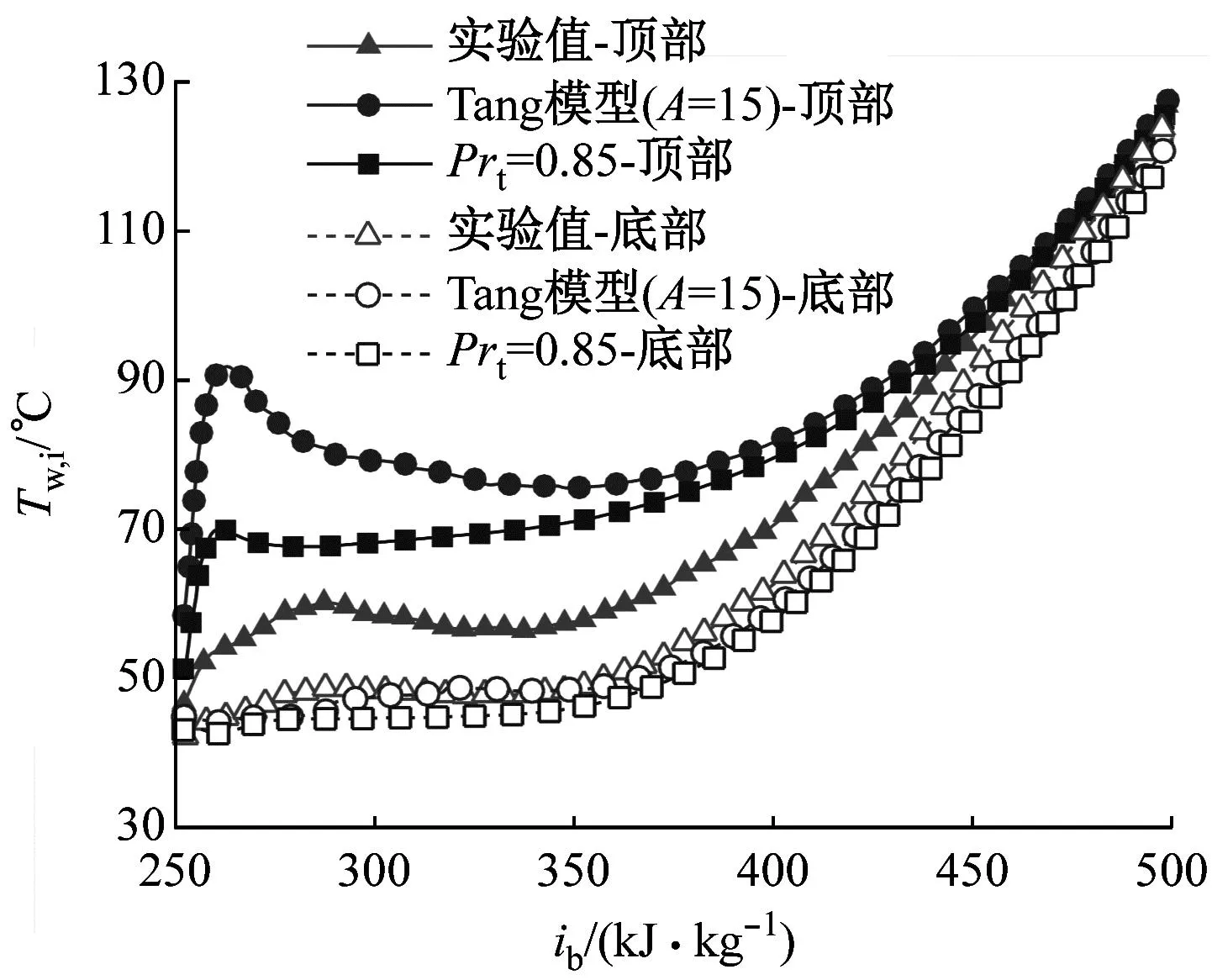
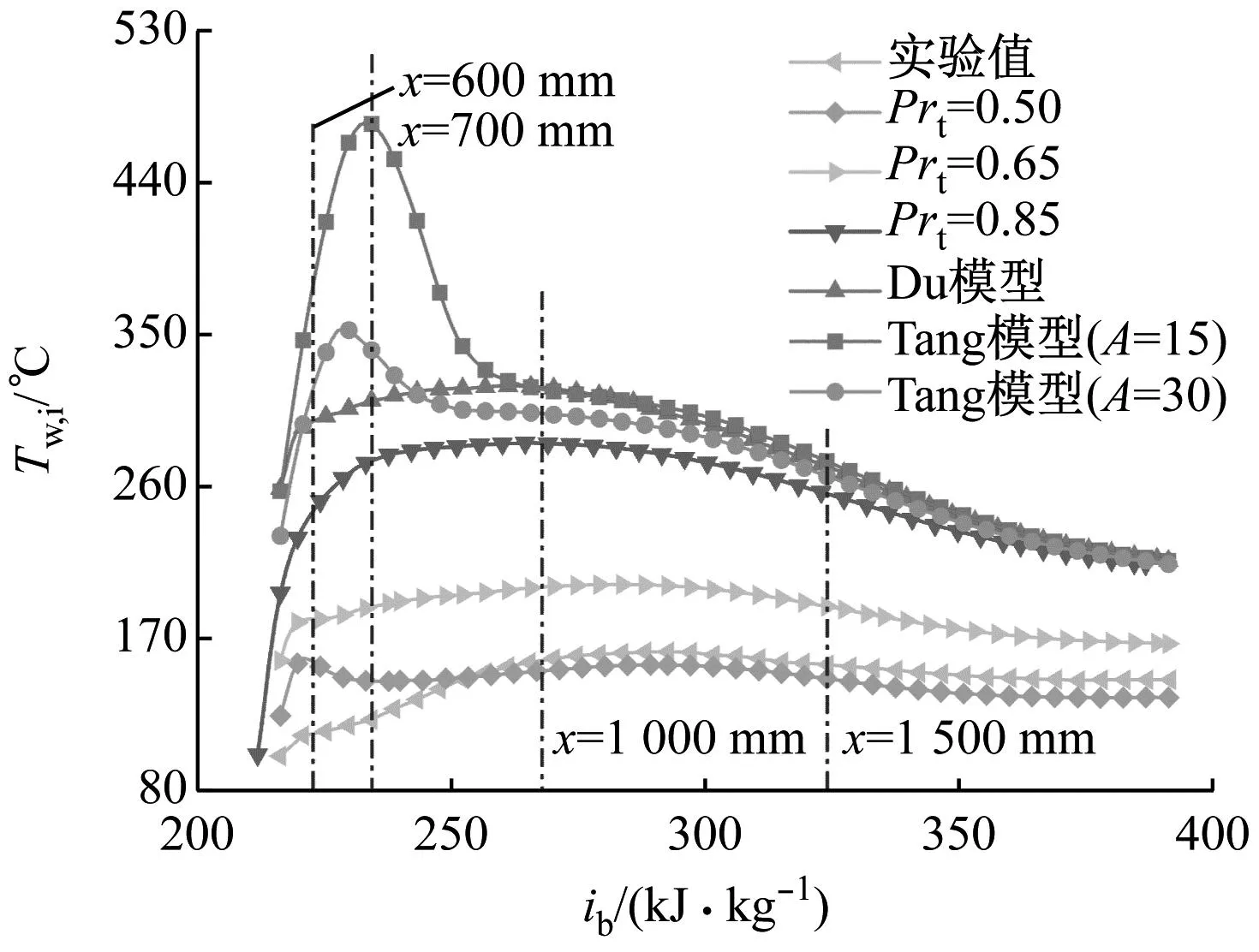
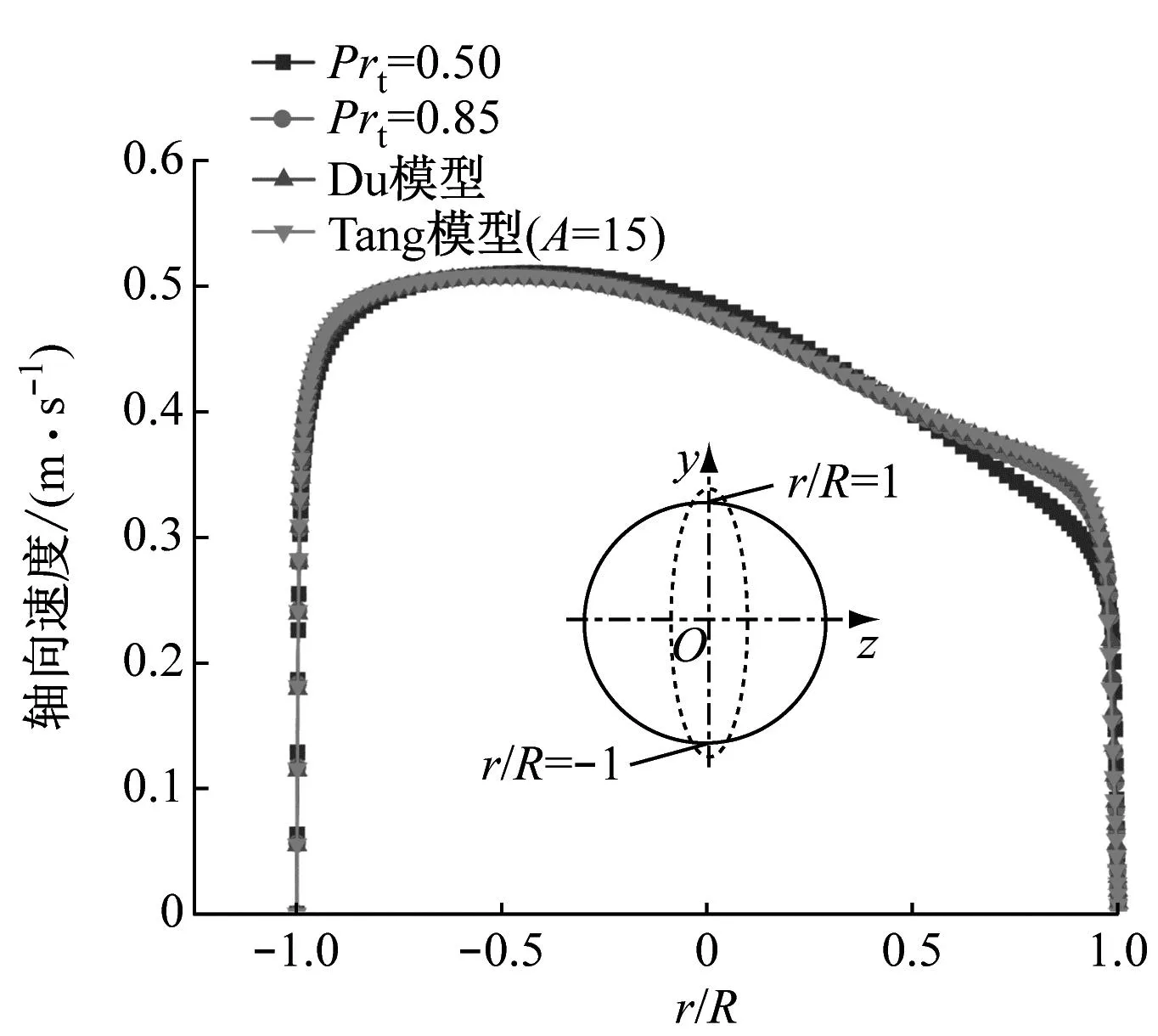
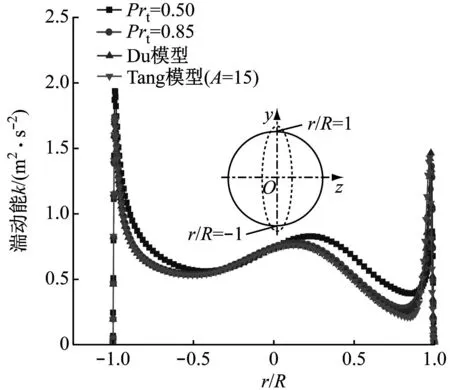
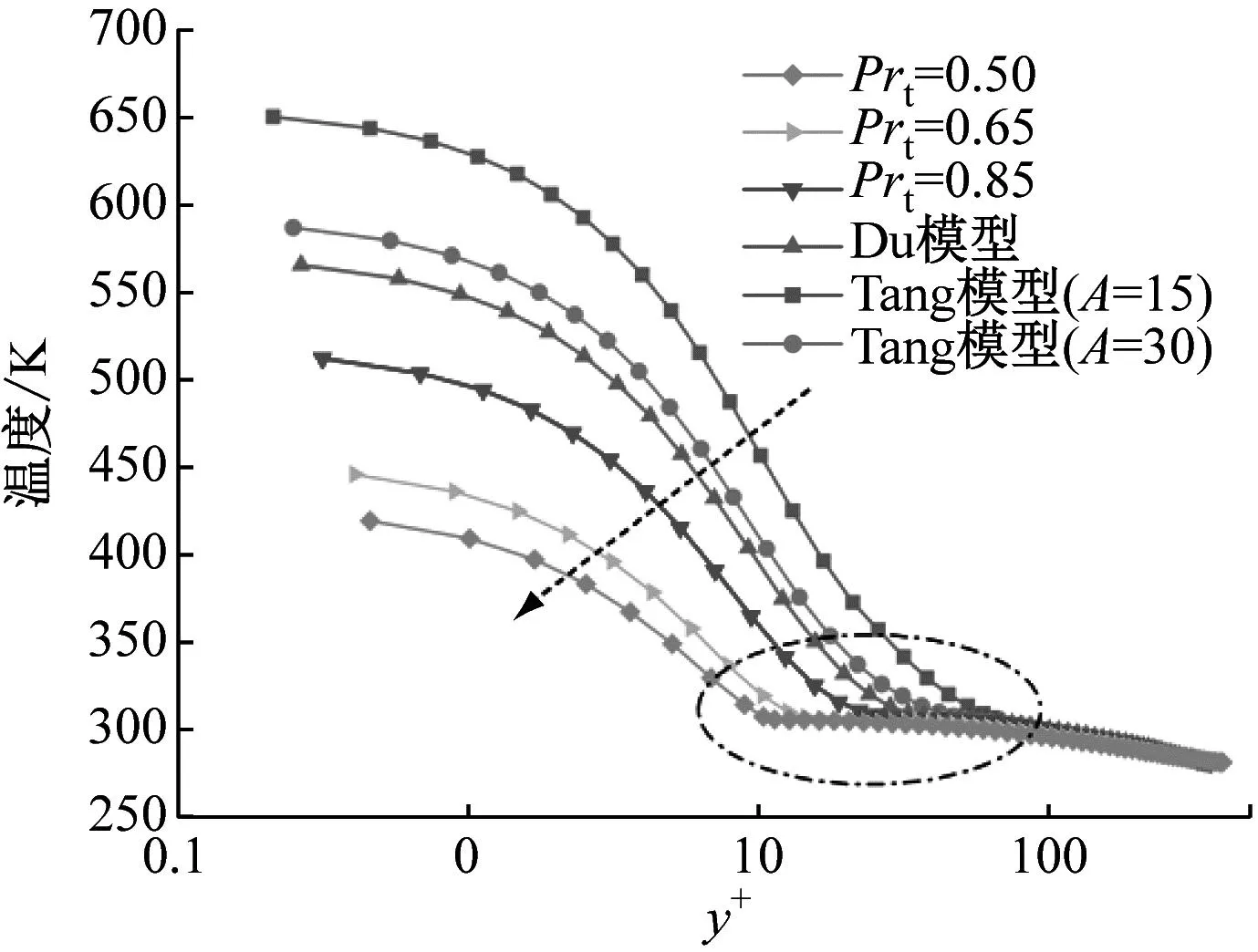
为与相应实验测量条件保持一致,表1中“TS”“TL”系列工况入口设置为质量流速入口,“A”系列工况入口设置为质量流量入口,出口均设置为压力出口,入口发展段和出口缓冲段的壁面设置为绝热。加热管壁设置为均匀热流密度且为无滑移边界。边界参数与实验工况相同,具体见表2。本文所选择的验证工况均处于临界点附近,CO2物性变化明显,典型热物性参数具体范围为:1.14 kJ/(kg·K) 表2 验证工况 控制方程采用有限体积法进行离散,压力-速度耦合运用Simplec算法求解,动量方程和能量方程采用Quick格式,动量方程中的压力项应用Body Force Weighted离散,除密度采用二阶迎风格式外,湍动能和耗散项均采用一阶迎风格式以获取更优的收敛性能。计算过程中,sCO2真实气体效应物性参数调用自基于求解器内嵌的NIST物性库所生成的查找表,变Prt修正模型通过UDF(User-Defined Functions)载入Fluent软件求解器。 为了验证SSTk-ω湍流模型采用定常Prt=0.85模型开展预测的准确性和可靠性,基于Theologou等[12]和Adebiyi等[13]的实验结果,开展了强、弱浮升力效应下的仿真验证。 2.1.1 弱浮升力效应 图4给出了弱浮升力效应下(工况 TS1、TL1、A1和A2)定常湍流普朗特数(Prt=0.85)模型对圆管内壁温Tw,i的预测值与实验值随主流焓值ib增加的对比结果。图4(a)的结果表明该工况下的浮升力还不足以使上下管壁产生明显的温度差,3条母线处的模拟值与实验值在趋势和数值上均有着较高的吻合度。图4(b)~图4(d)中的工况下受热流密度q和管径d增大的影响,sCO2顶部和底部温差略微增大,但采用Prt=0.85开展仿真的计算结果仍能较好地预测壁温的变化趋势,且顶母线处壁温预测偏差小于5 K。以上验证结果表明,浮升力较小时,采用Prt=0.85时模型具有较好的预测可信度。 (a) 工况TS1 2.1.2 强浮升力效应 浮升力效应随管径d的增大和热流密度q与质量流速G比值(q/G)的增加愈发显著,直观反映于上下壁温差[19-21]。图5给出了强浮升力效应下(工况 TS2、TS3、TL2、TL3、A3和A4)定常湍流普朗特数(Prt=0.85)模型对壁温预测值与实验值的对比结果。图5(a)、图5(c)、图5(e)的结果显示,强浮升力效应下,当q/G相对较小时,顶母线处壁温预测值较实验值存在明显偏差,存在高估或者低估上壁温的现象。而随着q/G增大,浮升力进一步加强,如图5(b)、图5(d)和图5(f)所示,两者偏差进一步加大,上述现象在顶母线处壁温预测时尤为突出。由此可见,强浮升力效应下仍采用Prt=0.85开展sCO2湍流换热预测将变得“力不从心”。 (a) 工况TS2 由于强浮升力效应下Prt=0.85模型的预测效果不佳,本节尝试引入典型Prt修正模型,结果如图6所示。由图6(a)和图6(b)可知,传热恶化严重时,所嵌入的变Prt修正模型并未能改善预测性能。其中,针对图6(b)中内径为8 mm的水平圆管,Du模型计算值在趋势上与Prt=0.85时的近乎一致,上壁温预测值略偏高(受限于构造形式,Du模型无法应用于4 mm管径的修正)。然而,Tang模型在温度预测上的表现比Prt=0.85时更差,尤其是在入口处出现非常尖锐的上壁温峰值,该峰值随着A增大而降低。这是因为边界层缓冲层中Prt=0.85+Pr/A(Pr恒为正值),A越大,缓冲层的Prt越小。可以设想,当A趋于无穷大时,Tang模型将会无限逼近Prt=0.85时的壁温预测值。 (a) 工况TS3 图6(c)和图6(d)所反映的传热恶化程度较图6(a)和图6(b)的相对较轻。其中,如图6(c)所示,载入Du和Tang等提出的Prt模型修正后,在加热段下游,上壁温预测值更加接近于实验值,但变化趋势并无明显改善,同时下壁温预测值与实验值的差异略微扩大。当q/G进一步增大使得浮升力效应加强时,Du模型和Tang模型的温度预测值均更加偏离实验值。综合图6可知,利用变Prt模型开展计算所得的壁温预测值均大于Prt=0.85时的预测值。这是由于变Prt模型在黏性底层、过渡层和湍流核心区的湍流普朗特数均不小于0.85,而根据能量方程(3),湍流普朗特数所在项为湍流扩散项,湍流普朗特数的增大使得湍流掺混效应减弱,传热性能下降,继而壁温升高,这与文献[7]和文献[22]的结论一致。 上述结果显示在强浮升力效应工况下,现有典型的分段赋值变Prt修正模型对水平sCO2流动传热的预测改善效果不佳。本节基于工况 TL3这一典型强浮升力效应工况进行计算,从主流(“宏观”)、边界层(“微观”)2个层面深层次探究Prt模型对水平sCO2湍流传热模拟的影响。为了更加全面地揭示Prt的影响规律及作用机制,此处直接改变定常Prt值进行计算分析。 2.3.1 湍流普朗特数模型对轴向主流的影响 图7在图6的基础上添加了不同定常Prt的计算结果,据前文可发现Prt的影响更突出体现在对上壁温的预测上,因此图7重点展示水平圆管上壁温的分布。由图7可以看出,Prt的减小会使上壁温大幅降低,其预测值的整体趋势与实验值更加吻合。 图7 不同湍流普朗特数模型上壁温预测值与实验值 图8给出了沿轴向方向不同截面处各Prt时计算得到的中垂线处速度轮廓,其中,图8(a)为x=600 mm截面处的速度分布,r为径向距离(某点到圆心的距离),R为半径。从图中可以发现,不同Prt模型获得的速度分布曲线底部几乎重叠,但顶部已呈现较为明显的差异。随着加热的持续进行,Prt对主流速度的影响进一步凸显,顶母线近壁区的轴向速度差异继续扩大。在x=700 mm截面处的顶母线近壁区,速度随Prt的增大而增加。其中,Tang模型所得速度轮廓在近上壁处出现第二速度峰值(半M型),这是Prt的增大使得流体传热受阻,浮升力效应影响进一步加剧的结果,即顶部积聚的“类气态”sCO2愈发增多,二次流向下动量输送中止,使得上半区域形成第二速度峰值。当sCO2流经x=1 000 mm截面处时,除Prt=0.5时外,其他模型所得速度剖面均于近壁处变平,直至加热段下游x=1 500 mm处,顶部流体速度已高于底部流体。 (a) x=600 mm 图9给出了不同Prt模型所计算得到的各截面处湍动能分布。由图9可以看出,Prt=0.5时在4个截面处的湍动能均呈现出底母线的比顶母线的高的特点,但Prt=0.85以及Tang模型、Du模型的载入使得湍动能在各截面呈现出一系列特殊现象。与图8中截面的上母线近壁区速度分布相对应,Prt的增大使得该区域速度剖面变平,甚至在r/R=0.85处形成第二速度峰值。这虽使紧贴上壁处的速度梯度增大,湍动能强度继而增大,但r/R=0.85处速度峰值带来的零速度梯度直接导致该径向湍动能最低值的出现,该湍动能值对流动传热起着更为决定性的负面影响(这一点反映在图9(a)中),因此传热恶化加剧。 (a) x=600 mm 2.3.2 湍流普朗特数模型对径向边界层的影响 由于动量传递和对流换热主要受速度边界层和热边界层的影响,以及Prt的影响集中体现在加热段上游的“类液区”,因此选取加热初始段x=600 mm处典型截面进行边界层层面的深入分析。鉴于不同Prt对底母线近壁区的各参数影响并不显著,因此下述分析将基于该截面中垂线处顶母线近壁区径向参数的变化展开。 图10(a)给出了近壁区的温度轮廓。从图10可以发现,对于定常和非定常Prt,Prt的减小使得壁温下降,同时热边界层厚度δt亦变薄,对流换热得到增强。图10(b)则展示了不同Prt模型计算下Pr的变化,由图10(b)可以看出,随着定常Prt的减小,Pr峰值变化不大(Pr与比热容cp的变化近乎同步,峰值所在处为拟临界点,Pr峰值附近为大比热区),但大比热区会朝缓冲层与黏性底层移动并靠近,边界层内(占据着绝大部分的热阻)传热热阻下降,这再次佐证了sCO2传热性能的上升。从图10还可以看出,变Prt模型时大比热区相较于定常Prt模型时更窄,Pr峰值亦更低,且均位于对数律区。而从图10(c)中近壁区Prt分布可以发现,针对Tang模型,A值的调整不仅会影响Prt峰值大小,还会影响Prt的分布。A值增大即模型缓冲层的Prt减小,会使得Prt整体轮廓沿无量纲距离y+左移,但峰值仍位于对数律区内,且与Pr的分布较为一致。但对于Du模型,Prt峰值与Pr峰值错位分布,Prt峰值已进入缓冲层。图10(d)展示了湍动能的分布,可以发现在y+<60紧贴壁面处,湍动能随着Prt的增大而减小,3个定常Prt和3个变Prt模型均在y+≈60处完成了数值高低的转换,而该处附近(对应图8中近上壁速度剖面的峰值处)的湍动能大小对sCO2传热起着更为主导的作用。 (a) 温度 (1) SSTk-ω低雷诺数湍流模型中Prt=0.85的设置在弱浮升力效应情形下能够比较可靠且准确地预测sCO2在水平管内的流动换热,而在强浮升力效应下则会产生较大偏差。 (2) 现有典型的分层赋值变湍流普朗特数修正模型应用于水平sCO2在弱浮升力效应工况下的传热模拟收效甚微,其并不能显著提升SSTk-ω模型的预测性能。 (3)Prt模型对sCO2湍流传热RANS计算具有深层次的影响,且对上壁区的影响显著大于下壁区。在轴向主流方面,Prt的增大会加剧浮升力效应,这使得上壁区出现第二速度峰值,进而影响顶母线近壁区的湍动能分布。边界层方面,Prt越小,上壁区热边界层越薄,大比热区往壁面靠近,传热热阻相应减小,壁温预测值随之下降。 (4) 后续针对水平sCO2传热计算Prt修正时,应更多聚焦于浮升力影响显著的上壁区,同时可在管径修正因子和压力修正因子的基础上,加入q/G修正因子,以更准确地反映浮升力影响。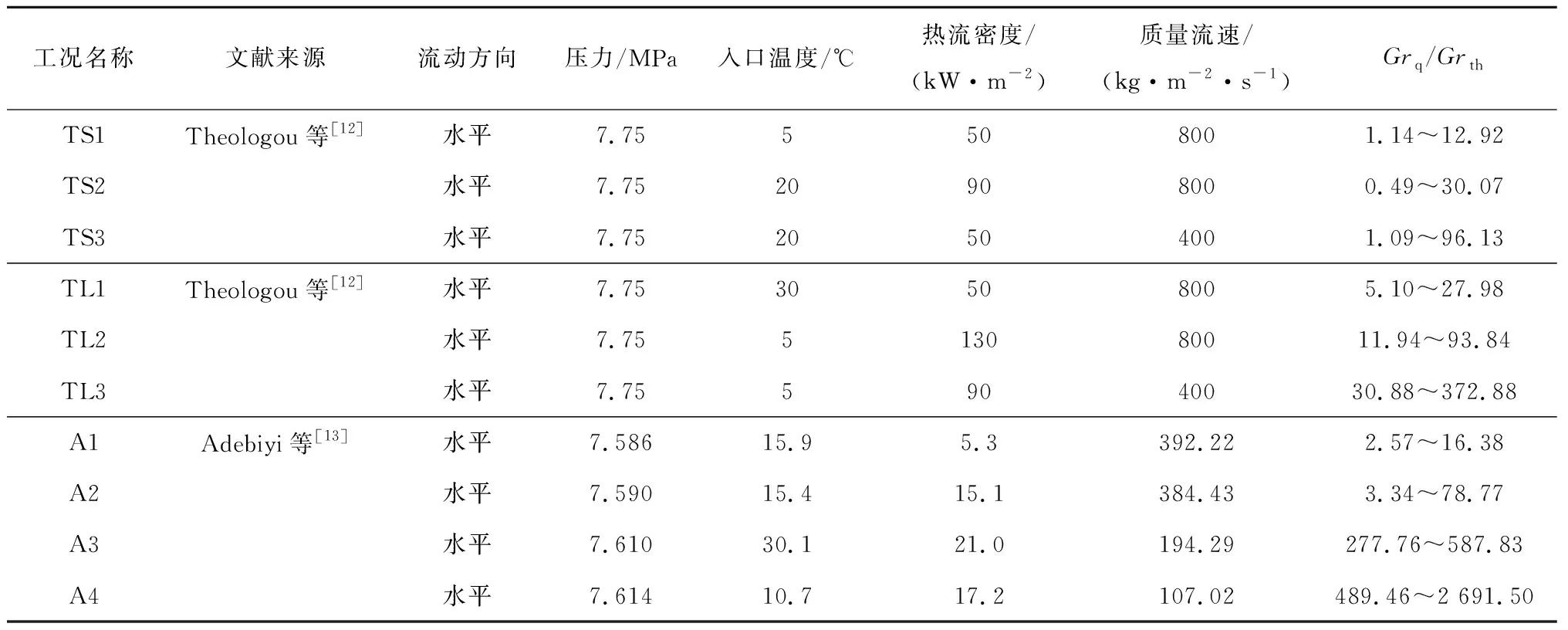
2 结果与讨论
2.1 恒定湍流普朗特数(0.85)模型对壁温的预测

2.2 变湍流普朗特数修正模型对壁温的预测
2.3 湍流普朗特数模型对水平sCO2流动传热的影响
3 结 论
