基于视觉的地外天体探测器着陆测速
2023-12-30赵尔迅张科备高晶敏
张 洋,赵尔迅,张科备,高晶敏
1. 北京信息科技大学, 北京 100192 2. 北京控制工程研究所, 北京 100094
0 引 言
根据我国未来深空探测任务的发展规划,地外天体附着采样探测是我国未来十到二十年深空探测领域的重点发展方向之一[1-2].为了顺利完成着陆探测任务,需实时估计探测器的下降速度,为探测器的自主制导、导航与控制(guidance, navigation and control,GNC)系统提供重要参考依据,保证探测器能够安全、准确地降落在天体地表.2021年5月成功着陆火星的天问一号通过惯性+测距测速模块修正导航,解决高动态下惯性模块精度下降或计算错误的问题[3],测距测速传感器的精度及稳定性直接影响软着陆效果.
光学相机作为着陆导航敏感器[4]的主要测量单元,负责记录探测器着陆过程中的视频图像.利用光学相机拍摄的天体地形视频帧进行实时测速,可辅助探测器执行自主导航、自主障碍识别、自主定位及对准等任务.
在基于视觉的速度测量研究中,目前代表性的方法主要分为如下两类:
(1)基于特征点匹配的测速算法.
文献[5]使用火星探测器搭载的光学相机拍摄降落过程中的图像,通过特征点匹配得到不同图像上对应点的像素位移,再根据惯性传感器的姿态信息和高度传感器的高度变化,推算出像素位移对应的实际位移并除以拍摄时间间隔,即得到探测器着陆速度.文献[6]提出一种基于图像序列特征点匹配跟踪的无人机测速方案,同时结合惯性导航装置、高度计和可见光或红外摄像机的多种测量信息,计算无人机的瞬时飞行速度.文献[7]将光流和尺度不变特征变换(scale-invariant feature transform, SIFT)数据进行卡尔曼滤波融合,实现无人机的速度测量.文献[8]建立实际距离到像素距离的二维映射表,将特征点在时间序列中的像素位置坐标转换成实际位置坐标,求取运动距离再除以单位时间,从而获得速度信息.以上方法存在天体表面地形单一造成特征点难提取以及特征点随着下降运动偏移出相机视域的问题,并且需要借助其它多传感器测量数据协同计算.
(2)基于深度神经网络的测速算法
在车辆测速方面,文献[9]利用EfficientNet网络对提取的光流特征进行速度预测,该方法只适用于近视距测速场景,而在远视距的航天器着陆测速中,由于受成像透视效应的影响,网络难以拟合,测量精度严重下降.文献[10]提出了一种基于长短期记忆网络(long short-term memory,LSTM)的车速测量方法,综合道路类型、交通状况、加速度等数据,通过当前时刻信息预测下一时刻速度.该算法需要的数据类型和数据量较多,计算复杂费时.以上方法无法解决远距离成像时透视效应对测速精度的影响,均不能直接应用于地外天体探测器着陆测速.
为了克服上述问题,本文提出一种基于深度学习的视觉测速方法:应用递归全对场变换(recurrent all-pairs field transforms,RAFT)[11]光流算法提取连续视频帧的光流场,然后通过卷积神经网络提取光流场对应的特征向量,最后构建长短期记忆网络对提取的光流特征与速度进行拟合.在实验测试中,与基于EfficientNet网络[9]的测速算法进行对比,证明提出的测速模型在引入时间序列后能够有效克服透视效应的影响;与基于时序前向传播网络回归模型[12]的测速算法进行对比,证明本文的长短期记忆网络具有更高的着陆全程测量精度.本文方法仅利用了光学相机获取的视频图像,无需依赖其它高精度传感器的测量数据,既可以解决传统测速算法特征点脱离视域的问题,也可以改善远距离成像中视觉透视效应对测速精度产生的影响.
1 视觉测速算法
本文构建LSTM长短期记忆网络训练测速模型,实现基于光流特征提取的连续视觉测速.该方法的前提是通过天体环绕探测任务提前获取降落地点的高精度地形、气候、大气密度等环境先验信息,用以构建降落仿真数据[13-14].核心思想是训练一个LSTM网络模型,用以拟合连续视频帧中的速度信息和实际速度,其中视频帧的速度信息由光流法获取,实际速度由降落过程的仿真建模获取.
本文提出的视觉测速算法总体框架如图1所示,实线表示模型训练过程,虚线表示实际应用过程.首先通过仿真模型模拟降落过程速度变化和降落相机拍摄的视频图像序列,然后采用RAFT递归全对场变换光流算法提取图像序列帧间变化光流场,再参考卷积神经网络(convolutional neural networks, CNN)提取特征的思想,构建卷积层和池化层提取光流场的特征向量,最后将特征向量和速度变化数据作为训练集输入到LSTM网络中进行训练得到测速模型.

图1 本文算法总体框架Fig.1 Framework of the proposed algorithm
1.1 视频帧光流场计算
光流法是估计空间物体在视频帧间运动信息的一种方法,光流反映了三维空间中的运动物体在二维像平面中移动的瞬时速度大小和方向,即速度矢量.根据原理的不同,光流法可分为稀疏光流[15]和稠密光流[16-17].其中稠密光流计算整幅图像或某一区域中所有点的偏移量,从而形成一个稠密的光流场.
本文采用RAFT递归全对场变换光流算法[11]提取天体地表视频帧的稠密光流特征.RAFT光流法计算过程如图2所示:通过特征编码器分别提取着陆视频相邻两帧中每个像素的特征向量,通过上下文编码器提取其中一帧的上下文信息特征;构建多尺度相关性查找表进行视觉相似性计算,用来表示两帧中每个像素对的相关性;更新迭代模块利用门控循环单元以及卷积操作,计算出残差光流作为补偿,并与上次迭代过程输出的光流进行叠加;最后经过邻域加权上采样恢复图像尺寸,生成光流场.该光流计算方法泛化能力强,对于单一背景运动的光流计算准确率高.
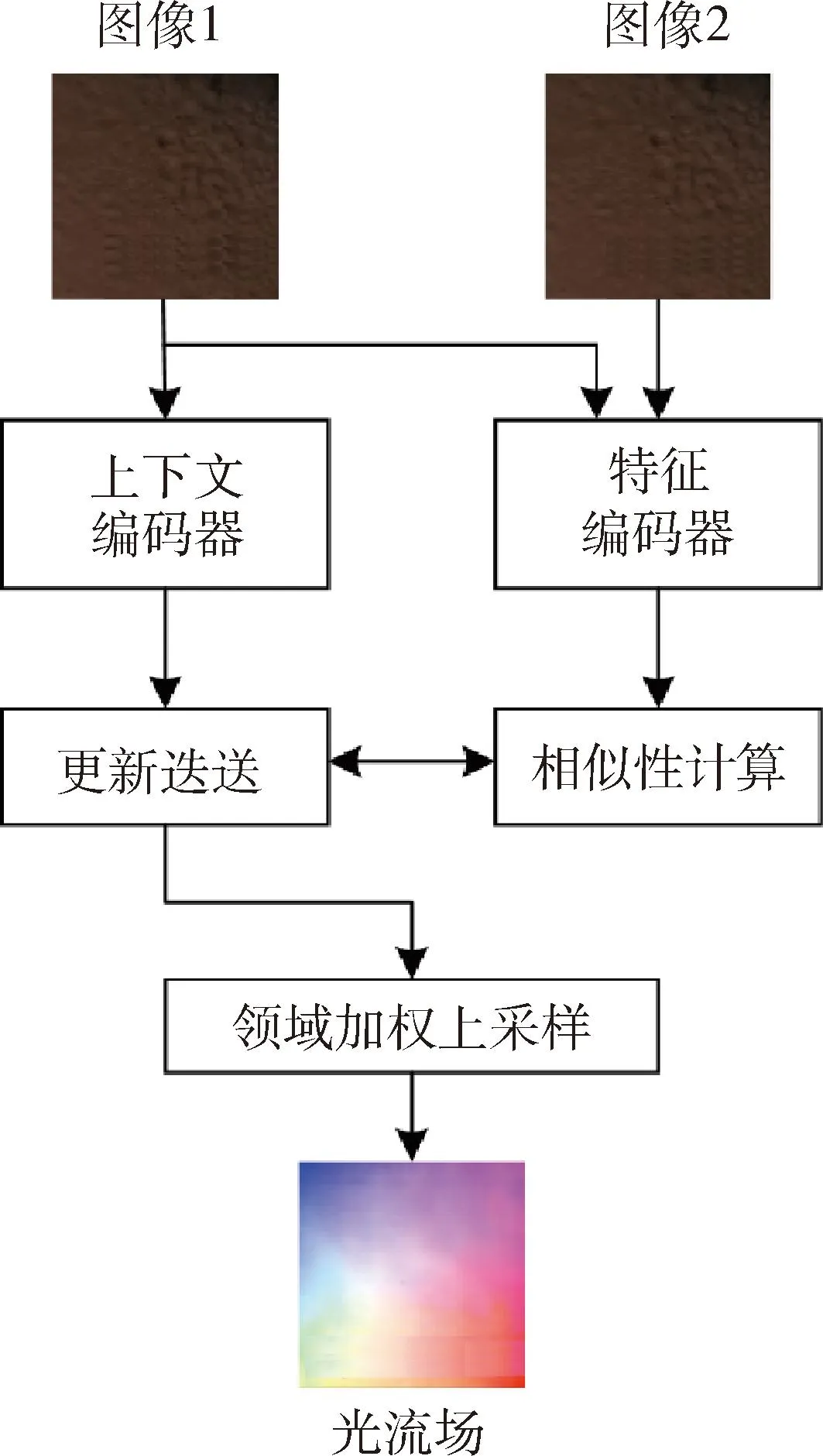
图2 RAFT光流场计算流程Fig.2 RAFT optical flow field calculation process
由于受火星表面气流的影响,相机的拍摄画面会以正下方为中心随机晃动.图2最后所得光流图是经过渲染后的可视化光流场,其中不同颜色代表速度矢量的方向,颜色深浅代表速度矢量的大小,从图中可知光流方向围绕中心向四周展开,且距离中心越远,速度矢量越大.
1.2 光流场特征向量提取
导航敏感器上的光学相机分辨率一般都在4 000×4 000 Pixel以上,虽能获取高分辨率的着陆视频图像,但过高的分辨率会导致光流法计算复杂耗时.另外光流法是通过帧间对应像素灰度变化估计像素速度矢量的,像素块越多,计算的准确率就会越低.考虑到RAFT光流法中特征编码器会将原始图像缩小为1/8,所以在进行光流提取前将视频帧尺寸缩小为8的整数倍,即256 pixel×256 pixel.
为满足实时测速的要求,必须通过尽可能简单的特征提取网络结构获取速度预测所需的有效信息.图像是每个像素点对应一个灰度信息,分为R、G、B三通道;光流场是前后两帧中对应像素的位移速度信息,分为x方向和y方向双通道.因此光流场与图像类似,实质上也是数据阵列,可参考CNN卷积神经网络提取特征[18]的思想对视频帧的光流场提取特征向量.
由于光流场是像素点在x、y方向的平面速度矢量,速度大小与光流方向无关.所以将光流场的两个通道合并为表示速度绝对值的单通道当量,公式如下:
(1)
其中,Vi,j为绝对速度,Vx为x通道速度,Vy为y通道速度,(i,j)为对应像素的坐标.
相较于原始图像,光流场包含的特征信息单一,不必使用复杂的CNN网络结构,以免特征提取过深造成错误的特征理解而发生过拟合.对整体256×256的光流场,使用步长为32的32×32×1卷积核,将其分为如图3所示的64个区块.该计算过程可表示为
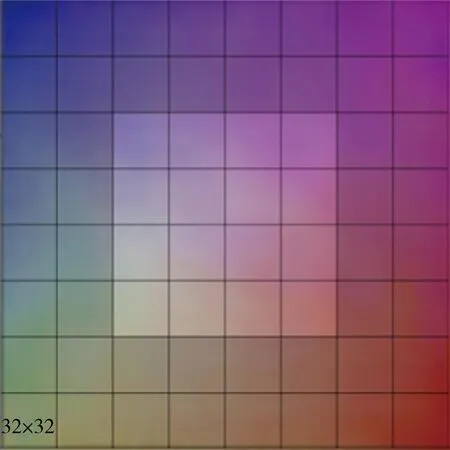
图3 光流场分块提取特征向量Fig.3 Eigenvectors extraction from optical flow field

(2)
其中,F为卷积后的特征值,f为卷积核,I为输入光流场,m,n为区块序号坐标.
因为光流场中心运动变化量低、特征少,为提高计算效率,提取出边缘两圈共48个区块的数据.对48个数据块进行平均池化操作,生成第t帧光流场的特征向量xt
(3)
1.3 基于LSTM网络的视频帧实时测速
(1)成像透视效应
探测器在下降着陆过程中,光学相机会产生透视效应[19],其最基本的特点就是成像目标“近大远小”.假设探测器下降速度不变,随着视距(地表目标与相机镜头之间的距离)的改变,同一地表目标在视频帧中的变化尺度不同,故不能直接根据光流场特征向量估算探测器着陆速度.
透视效应仅与视距有关,视距越近透视关系越明显.远处的物体接近透视灭点,所在相机中的成像小;近处的物体接近镜头,在相机中的成像大.当相机镜头以正前方的点为目标向其靠近时,图像中心点的位移为0,目标四周的点可以近似为从中心点出发围绕镜头做圆周运动,直至消失在视野外.根据角速度公式
(4)
当线速度v(真实运动速度)相同时,视距r越大,角速度ω(图像像素位移速度)越小,即感知速度越小.透视关系如图4所示,在探测器距离目的地8 852.92 m时相机视域为红线标注范围,距离3 154.04 m时视域为蓝线标注范围.假设真实世界中a点到b点与a′点到b′点之间的实际距离相同,若运动时间也相同,则vab=va′b′,根据式(4)可知ωab<ωa′b′.即运动速度相同的点在成像时,视距远则目标点对应的像素运动慢,反之视距近则目标点对应的像素运动快.
地外天体探测器的光学相机随着与天体表面距离越近,成像透视关系越强,这就造成在高处下降速度快时帧间对应像素变化小,在低处下降速度慢时帧间对应像素位移大.速度曲线与光流特征曲线无法一一对应,相同的光流特征向量可能对应多个速度值,不能准确计算实际着陆速度,所以一般的非线性回归方法无法解决视距变化范围大时的测速问题.
(2)LSTM网络结构与速度计算
为解决探测器着陆过程中光学成像透视效应造成的测速不精问题,构建LSTM网络对视频连续帧进行速度拟合.LSTM是循环神经网络(recurrent neural networks,RNN)的其中一种改良形式[20-21],与经典循环神经网络RNN相比,它能对输入的信息选择性的记录或遗忘,实现长时序预测.
本文的LSTM网络结构如图5所示,其中vt-1表示利用特征向量计算的上一时刻探测器着陆速度,训练时初始量设置为0;vt表示当前时刻探测器着陆速度;xt为当前时刻视频帧光流场的特征向量;ct-1为上一时刻网络隐层计算的单元状态,包含长期信息;ct为更新后当前时刻的单元状态.
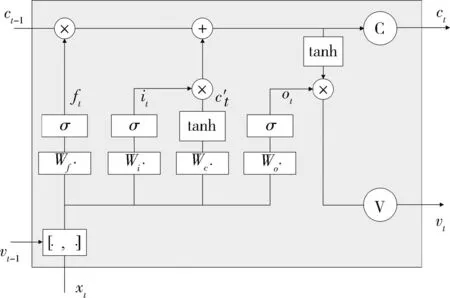
图5 LSTM网络结构Fig.5 LSTM network structure
将上一时刻输出的速度vt-1与当前时刻的光流特征向量xt通过contact的形式组合,采用遗忘门保留上一时刻单元状态ct-1的部分信息,遗忘门公式为
ft=σ(Wf·[vt-1,xt]+bf)
(5)
其中,σ为sigmoid激活函数;W和b分别为权重矩阵和偏置值.ft作为遗忘系数清除上一时刻单元状态中不重要的速度信息.
输入门与遗忘门的作用机制类似,但不同的是输入门生成输入系数it,用来记录保留上一时刻的速度信息和当前输入的特征向量
it=σ(Wi·[vt-1,xt]+bi)
(6)
单元状态计算模块根据上一时刻的输出速度与当前时刻输入的特征向量,使用tanh激活函数生成新单元状态的候选值
(7)
利用遗忘系数清除旧信息,输入系数添加新信息后,获得新的单元状态
(8)
与输入门的计算原理相同,输出门将特征向量xt与前一时刻速度组合,通过权重矩阵和偏置值计算输出系数ot
ot=σ(Wo·[vt-1,xt]+bo)
(9)
基于式(8)中新的单元状态,计算当前时刻探测器着陆速度
vt=ottanh(ct)
(10)
当前时刻的光流特征向量输入LSTM网络后会结合之前所有时刻的测速信息计算出当前速度,这样就避免了透视效应造成的当前时刻特征向量映射到之前时刻速度标签的问题,可实现利用连续视频帧准确计算探测器实时着陆速度.
2 实验结果与分析
为验证算法有效性,将本文方法、无时序的EfficientNet卷积神经网络[9]测速算法和加入时间序列的前向传播神经网络[12]测速算法进行对比测试.实验中以测试集结果的误差值曲线和平均绝对百分比误差(mean absolute percentage error,MAPE)作为模型测速效果的评价指标.MAPE是一种评价回归预测准确性的指标,常用于时间序列的预测,表示预测结果相较真实结果的平均偏离百分比.
2.1 数据集构建
本文采用NASA’s Eyes软件的仿真模型模拟地外天体着陆探测任务.以好奇号火星车降落任务的模型和数据构建训练集和测试集.
NASA’s Eyes是一款NASA官方推出的宇宙模型仿真软件,其中包含了火星模型和好奇号火星车下降全过程的仿真动画.着陆场景包含不同地形,视线方向可调,天气状况较好,成像清晰.通过调节成像视角模拟探测器下降时光学相机拍摄的天体地表画面,用于实验测试.图6为“好奇号”模型与降落画面.

图6 NASA’s Eyes“好奇号”模型与降落画面Fig.6 “Curiosity Rover” model and landing images in NASA’s Eye
好奇号火星车的着陆全过程分为:巡航装置分离阶段、火星大气减速阶段、降落伞减速阶段和反冲发动机减速阶段[22].在降落伞减速阶段,距离地面约8 km时隔热罩分离,降落雷达和光学相机开始工作,此时降落速度约为310 mile/h(140 m/s).从传感器开始工作到火星车安全着陆,时长约为140 s.
对光学相机拍摄的视频进行每秒10帧的画面取样,除去掉隔热罩刚分离时阻挡视线和降落前反冲发动机冲击火星表面激起灰尘阻碍光流计算的时段,视频时长为123 s,共提取出1230帧画面,速度从308 m/h下降到1.7 m/h.本组数据作为训练集进行训练.重新选取不同的降落视角模拟真实的降落任务,重复上述操作作为测试集,时长为125 s左右,共提取出1250帧画面,速度从308 m/h下降为1.7 m/h.
2.2 模型训练
综合考虑模型复杂程度和测试效果,搭建四层LSTM网络.网络的输入、输出均为单通道数据,隐藏层与输出层只在最后时刻连接.训练集共1 229个数据,抽取中间30%的连续数据作为验证集.
参考LSTM超参数设置[21,23],对训练集样本进行验证.设定最大训练轮数为2 000,四隐层神经元个数分别为32、64、64、32,隐藏层激活函数选用双曲正切函数,损失函数选用均方误差.Batch尺寸设置为200,初始学习率设置为0.01,在380轮训练后通过乘以因子0.218来降低学习率.为避免过拟合,加入正则化系数0.000 2,并在第三隐层后设置一个参数为0.2的Dropout层.最后使用Adam优化器,选用验证集损失最低的模型进行测试.
图7为LSTM网络训练过程的损失值变化,黑色曲线为当前损失值,红色曲线为平均损失值.图8为网络训练集拟合效果和训练集拟合误差,其平均均方误差为0.9748.由图7和8可知损失随训练次数增加而下降,训练集拟合效果优异.
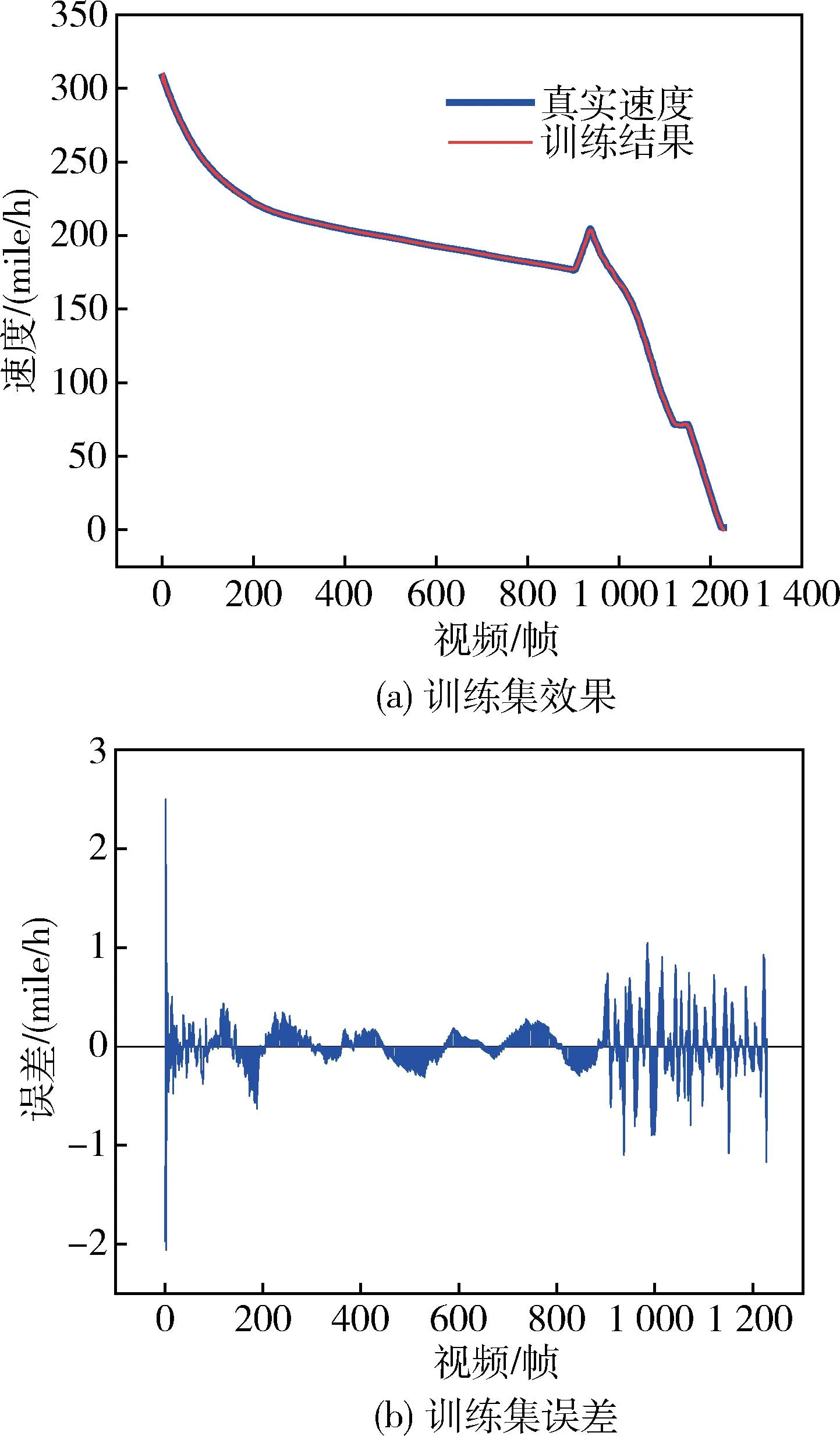
图8 训练集效果和误差Fig.8 Training results and errors of training set
2.3 模型测速效果对比
EfficientNet网络模型应用于车辆视觉测速[9],通过卷积神经网络提取特征并与速度标签拟合.前向传播网络是解决回归问题的常用模型,文献[12]给出了时序问题下的前向传播网络结构.将以上这两种方法与本文基于LSTM网络的测速算法进行对比测试.
分别将测试集数据输入到EfficientNet网络模型、前向传播网络模型和LSTM网络模型中进行测试,比较3种模型在探测器着陆全程的测速效果.速度测量值曲线和测量误差曲线如图9所示,从对比结果可以看出EfficientNet网络模型不具有时序特性,模型难以拟合,测速结果逐渐拟合到某一固定值并不断震荡,无法用于探测器长距离下降测速.相比之下,应用时序分析的前向传播网络和LSTM网络都能完成着陆全程的测速要求.
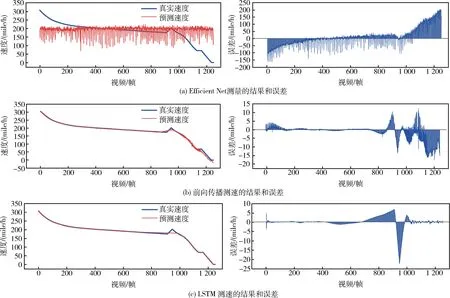
图9 不同算法测速结果对比Fig.9 Comparison of velocity measurement results between different algorithms
图9中第901~999帧为减速阶段转换时刻,无论是前向传播网络还是LSTM网络在该时刻附近都出现了测量误差波动,最大误差分别为13.65 mile/h(6.10 m/s)和22.76 mile/h(10.17 m/s).这是因为降落伞减速阶段(1~900帧)结束后反冲发动机并非立即启动,在减速阶段转换时,探测器速度先增后减,运动状态变化剧烈,难以提取相邻帧间的有效速度信息,不利于视觉测速.因此,重点考察降落伞减速阶段(1~900帧)和反冲发动机减速阶段(1 000~1 250帧)的测速效果.图10为降落伞减速阶段两种模型的测速效果曲线和测速误差曲线.图11为反冲发动机减速阶段两种模型的测速效果曲线和测速误差曲线.

图10降落伞减速阶段不同算法结果对比Fig.10 Comparison between different algorithms in parachute deceleration stage

图11反冲发动机减速阶段不同算法结果对比Fig.11 Comparison between different algorithms in engine deceleration stage
通过计算测量结果的平均绝对百分比误差 MAPE,进一步对比基于前向传播网络和本文基于LSTM的测速算法精度.不同减速阶段的MAPE指标和最大误差如表1所示.在降落伞减速阶段,前向传播网络的MAPE指标仅比本方法低0.34%,最大误差只相差0.52 mile/h(0.23 m/s),两种方法在该阶段的测速精度相差甚微.然而在反冲发动机减速阶段,本文方法的MAPE指标相较前向传播网络减小43.50%,最大误差仅为3.83 mile/h(1.71 m/s),本文方法在该阶段的测量精度明显更优.在整个着落过程中,本文算法的MAPE值(1.55%)也远小于前向传播网络(13.53%),因此提出的算法测速表现更稳定.

表1 测速评价指标对比Tab.1 Comparison of evaluation indexes on velocity measurement
在实际降落任务中,探测器越接近着陆点,测速精度要求越高,即反冲发动机减速段为着陆测速的关键阶段.在表1中降落伞减速阶段两种方法测速效果差别较小,但在反冲发动机减速的关键测速阶段,本文算法则明显优于前向传播网络.这是由于:1)随着时间的推移,前向传播网络的测量误差累积越大,其测速效果越差;2)前向传播网络模型本质上是求解输入输出的非线性关系,学习能力与训练样本有很大的关系.在降落伞减速阶段,着陆器运行平稳、减速均匀,训练集的降落数据与测试集相差不大,所以测试效果较好.而在反冲发动机减速阶段,着陆器状态变化相对剧烈,训练数据与测试数据相差较大,前向传播网络的测速误差就会增加.
综合考虑探测器下降过程中两阶段减速特点和关键测速阶段的精度要求,本文方法在整个着陆过程均能满足视觉测速要求,尤其在着陆关键阶段具有更精确的测量效果.另外,对测速效率进行记录,平均单帧计算时间为0.076 2 s,可满足实际工程中每秒至少10帧的实时测速需求.综上所述,本文提出的算法能够实现地外天体探测器下降的实时视觉测速任务.
3 结 论
为解决地外天体探测器着陆视觉测速中由于透视效应产生的图像速度特征与实际速度不匹配的问题,本文提出了一种基于LSTM长短期记忆网络的时序特征回归方法.利用卷积层提取光流场的特征向量,构建LSTM模型对特征向量和实际速度进行拟合,避免了视觉透视造成的影响.所得结论如下:
1)与同样应用时序特征的前向传播网络回归算法相比,本文方法在整个降落阶段和关键的发动机反冲减速阶段MAPE指标分别降低了11.98%和43.50%,测速精度更高;
2)提出的方法可以在高精度地外天体降落任务仿真模型的基础上训练测速网络,以满足实际测速要求;
3)由于仅依靠光学相机作为测速手段,该方法计算量小、硬件要求低且工作稳定,在实际应用中既可作为着陆导航敏感器的测速单元辅助执行自主导航任务,又可在其它测速传感器出现故障时作为临时备选方案使用.
未来的研究工作将重点解决减速阶段转换时刻测量精度下降的问题,并在不同着陆场景和探测器降落姿态变化较大的情况下进行测试,以进一步提升算法的泛化性能.
