一种基于双目视觉的立方星位姿参数估计算法
2023-12-30张杜祥
张杜祥, 刘 成
1. 中国科学院国家空间科学中心复杂航天系统综合电子与信息技术重点实验室, 北京 100190 2. 中国科学院大学计算机科学与技术学院, 北京 100049
0 引 言
立方星作为微小卫星具有成本低、体积小、研制周期短的特点[1],广泛应用于航天领域.立方星失去动力后会影响其他卫星正常运行,其结构参数和位姿估计对立方星回收有重大意义.立方星作为小卫星具有标准结构,形状与立方体相似,以10cm×10cm×10cm的规格称为1U,多个1U的立方星通过结构件组合可形成1U、2U、3U、6U和12U等相关规格[2].
立方星属于已知结构信息的非合作目标,非合作目标的位姿估计可分为基于图像[3-4]、基于点云[5-6]和图像点云相结合[7-9]的3种方法,后两类方法需要生成点云数据,在空间应用场景中计算量高,较为局限.完全依赖图像的位姿方法又分为基于几何特征[10]和基于点特征[11]的方法,基于特征点的方法对目标的局部特征要求较高,对没有局部特征或特征不清晰的目标不够通用,基于几何特征的方法只需要获取目标的矩形或圆形特征,进而实现对目标的位姿估计,在多数场景中有所应用.但通用的边缘提取算法存在鲁棒性差的问题,且局限于使用单一的几何特征确定目标信息.
针对空间环境中特征提取鲁棒性较差的问题,文献[12]将Sobel算子结合Hough线变换提取目标星体和帆板的边缘,但在实际场景中由于光照不均和目标旋转等情况导致提取效果差.文献[13]提出一种结合聚类、阈值分割和形态学操作的边缘提取方法,但提取的边缘为目标最大连通域,无法提取出目标连通域内的边缘信息.上述方法提取特征的能力有限,在图像对比度低时鲁棒性差,需要寻找更有效的方法实现目标边缘特征的提取.
针对空间中的矩形检测问题,文献[14]依据斜率的关系判别矩形特征.文献[15]提出了近距离矩形特征的拼接方法,通过两个相机的矩形信息拼接出目标完整信息.然而,现阶段的利用矩形信息的位姿估计方法都聚焦于单个矩形平面和平面上标志物的信息,并未考虑矩形之间存在的组合关系.立方星由于其体积较小,在图像中会以多个矩形组合的方式存在,针对矩形组的检测和判别对立方星位姿估计有很大的意义.
对上述非合作目标应用中出现的问题和不足,本文针对立方星目标提出了一套整体的设计方案框架,通过提取图像中目标关键顶点实现对结构和位姿参数的估计,包含边缘提取、多边形检测与筛选、目标关键顶点判别和目标规格判别与位姿估计4个部分,本文在实现整体框架的同时,也对部分算法进行了优化改进:
1)在边缘提取部分,针对当前传统Canny算法提取目标特征鲁棒性差的问题,本文提出结合HED网络和二值化形态学处理的算法,实现了图像边缘信息的强鲁棒性提取;
2)在目标关键顶点判别部分,设计了一套共边双框关键顶点判别算法:基于预处理好的多边形组,通过双框选择、公共边顶点判别和体对角顶点判别3个步骤,实现不同视角下的关键顶点判别,为后续的参数估计提供有效的对应点信息.
1 算法框架
本文的整体框架如图1所示.双目相机左右视角灰度图像经过HED网络结合二值化形态学处理的边缘提取方法生成二值边缘图像,通过多边形检测与筛选获得包含目标矩形信息的多边形组,并设计算法判别目标关键顶点,结合左右视图的对应点计算三维坐标,估算目标的规格和位姿信息.

图1 算法框架Fig.1 Algorithm framework
1.1 边缘提取
Canny边缘检测方法被广泛应用于空间非合作目标边缘提取过程,从边缘图像中提取出目标的几何特征,便可进行后续的位姿估计.但传统的Canny算法适用于成像效果好的场景,当场景中光照不均时,无法较好地实现完整的边缘提取.
HED网络于2015年提出,以VGG16网络为基础框架实现了端到端的室外场景中的景物和目标边缘提取[16].网络去除VGG16的最后一个池化层和用于分类的全连接网络,节省了在全连接层中消耗的参数资源[17].HED提出了一个整体嵌套的架构,将网络每一个块最后的卷积层提取后实现多通道融合,输出最终的边缘图像,整体网络结构如图2所示.
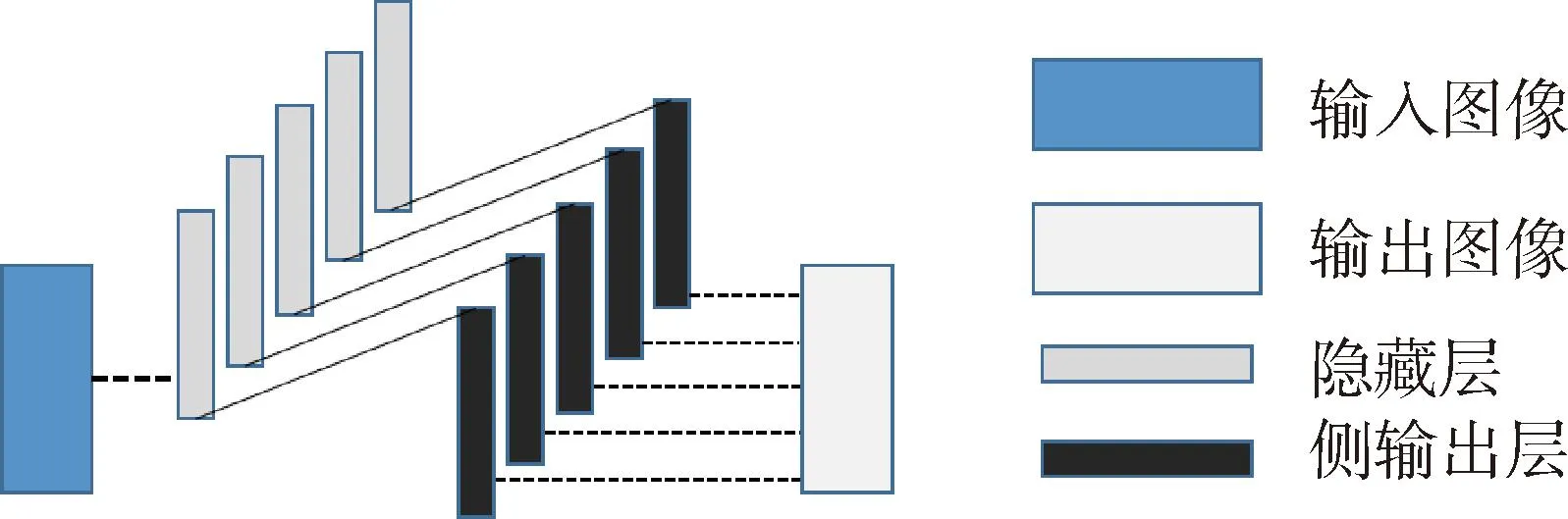
图2 HED网络结构Fig.2 HED Network Structure
本文依据太空中的成像环境和实际效果调整了HED网络权重,并优化了最终的输出结果,将其应用在空间非合作目标的边缘提取中.本文算法利用HED网络结合形态学处理的闭操作,提取场景灰度图像fgray(x,y)的边缘信息,在成像效果较差的情况下也能够生成具有较强鲁棒性的二值边缘图像fedge(x,y).

图3 未修改权重与修改权重对比图Fig.3 Comparison diagram of unmodified weight and modified weight
(1)
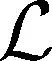
(2)
空间中的光照影响会导致成像效果较差,HED生成的图像会出现边缘断连现象,影响后续的多边形检测.为使算法适应当前应用场景,本文引入二值化形态学处理:将边缘图像基于给定阈值进行二值化分割,增强有效边缘信息的强度,再结合形态学处理中的闭操作,通过先膨胀后腐蚀的操作,连通邻近的断连像素.闭操作将缺口连接的同时并没有影响其他边缘效果,为后续检测提供有效的特征信息,对比效果如图4所示.

图4 断连与无断连对比图Fig.4 Comparison diagram of disconnected and connected
1.2 多边形检测与筛选
多边形检测与筛选是立方星体对角顶点判别的预处理过程,二值化边缘图像fedge(x,y)包含目标的有效矩形信息,对图像进行多边形检测提取矩形特征,再筛选出包含目标矩形信息的多边形组进行后续判别.
多边形检测包括轮廓提取和多边形近似两部分:
(1)轮廓提取
首先对二值化的边缘图像进行轮廓提取,SUZUKI[18]提出的基于边界跟踪方法判别二值图像像素的连通域,从而实现轮廓提取:根据光栅扫描法从左至右,从上至下提取出图像中被1像素值所包围的孔边界连通域,为每一条新的边界赋予边界特定的编号,检测的边界以轮廓拐点坐标的形式存储在数组当中,避免了保留轮廓所有像素点带来的数据量.
(2)多边形近似
接着采用DOUGLAS-PEUCKER迭代方法[19]拟合每一个轮廓的逼近折线:判断当前轮廓中距离首尾连线最大的点是否大于给定的阈值Tr,若大于阈值,则将曲线以最大点划分为两段分别处理,反之将该曲线近似为线段,直到轮廓全部被折线段近似.
本文将连续折线段顶点以集合的形式存储,即各个多边形的顶点信息,多边形Di表示为
Di={p1,p2,…,pn}
(3)
其中,pj对应多边形按顺序连接的各个顶点坐标,pj=(xj,yj),n对应多边形Di边的数量.为保留有效的矩形信息,选取n大于3的所有多边形保存到集合当中,进行后续判别.
检测出图像中的多边形特征后,根据多边形顶点之间的像素距离信息对多边形进行筛选,保留与目标相关的多边形信息,筛选过程包含多边形去重和孤立多边形滤除两步:
(1)多边形去重
轮廓检测过程中多次的阈值分割导致多边形顶点列表存在重复,干扰判断,需对其去重.考虑到重复的多边形所有顶点坐标都会相同或相近,判断多边形Di和Dj的所有顶点距离,若多边形相邻点个数超过3个,则判定为两多边形重复,保留两者中面积更大的多边形实现去重,如式(4)和图5所示.
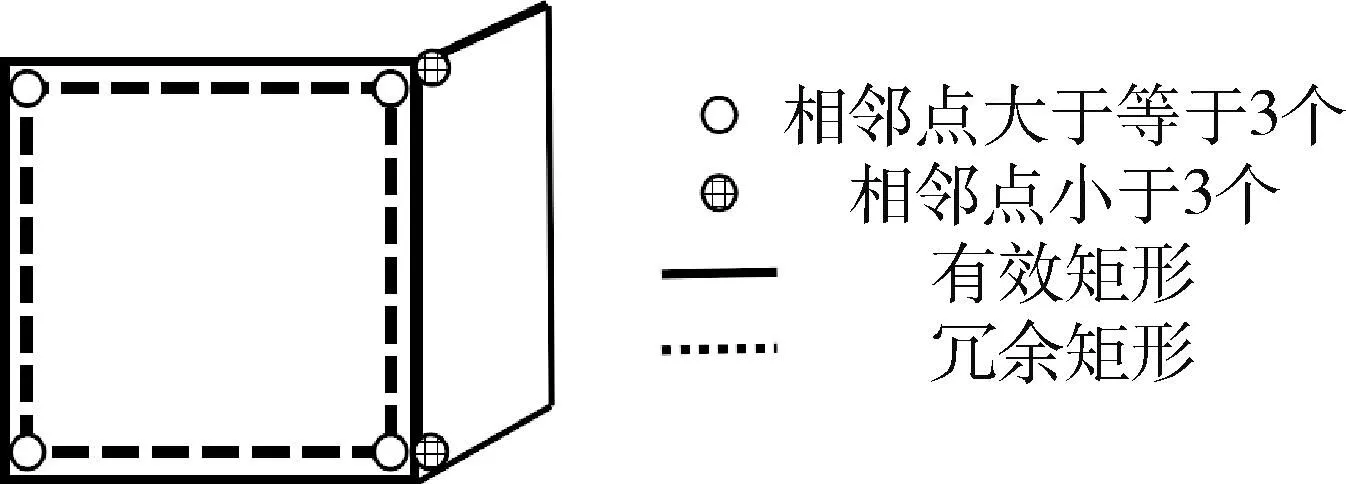
图5 多边形去重Fig.5 Deweighting of polygon
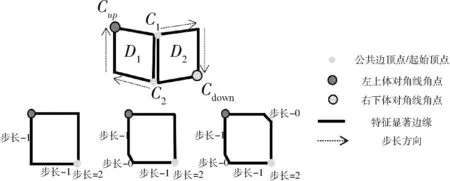
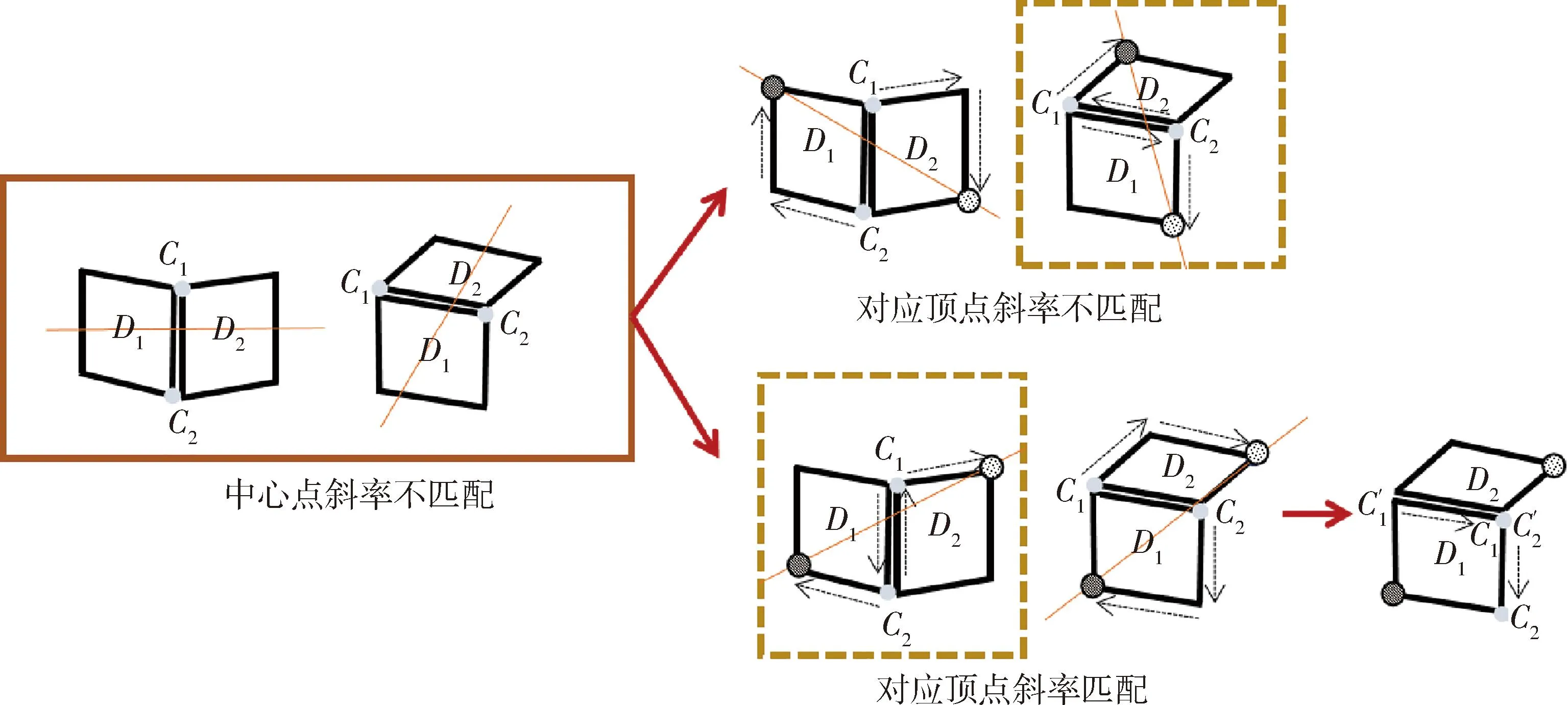
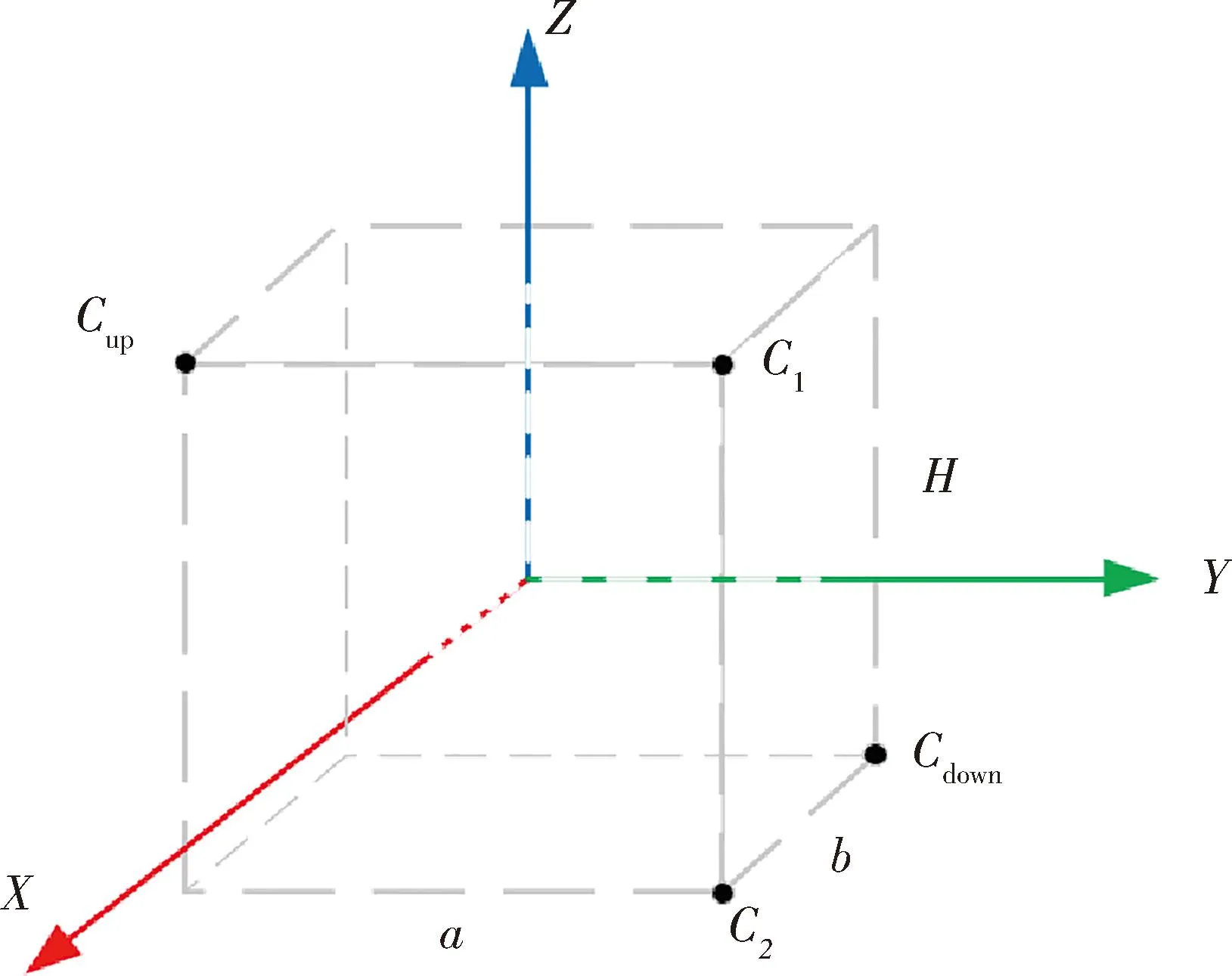
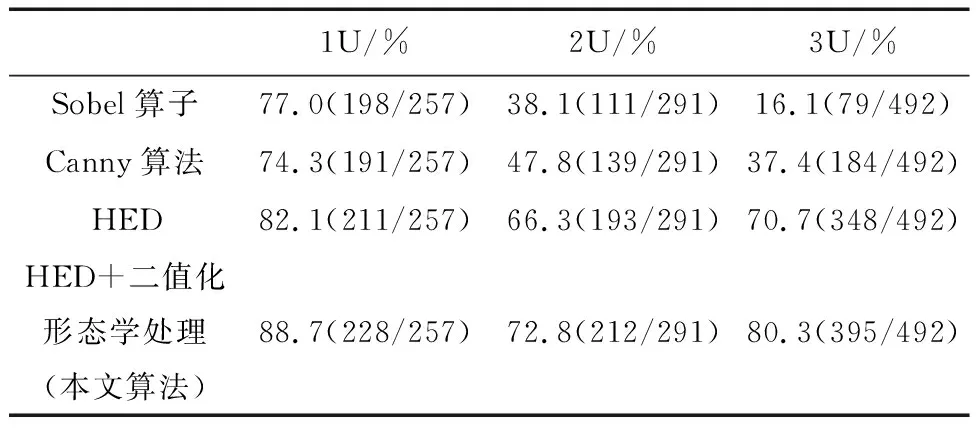
|Di{px}Dj{py}| (4) 其中:|Di{px}Dj{py}|表示多边形Di的像素点px与多边形Dj的像素点py之间的欧氏距离;Tr为设定的像素距离阈值,小于阈值则判别为相邻点. (2)干扰多边形滤除 视角中除立方星目标外,还可能会出现干扰判别的多边形,需要将相邻的多边形信息进行组合,滤除干扰的多边形:若多边形Di和Dj属于同一个目标,则会存在两个以上的相邻顶点,将其顶点信息进行组合;而场景中干扰的多边形与目标平面相邻顶点数量少于两个,对应的多边形不进行组合,如图6所示. 图6 干扰多边形滤除Fig.6 Interference polygon filtering 为获取有效的目标关键顶点信息,本节根据立方星目标矩形特征间的特殊位置关系,设计了一套共边双框关键顶点判别算法,用于判别目标公共边顶点和体对角顶点,包括共边双框选择、公共边顶点判别和体对角顶点判别: (1)共边双框选择 在相机视角中,立方星目标通常会呈现2~3个矩形平面的组合,当左右视图中多边形的数量大于等于两个时,计算各个多边形的中心坐标,将中心坐标两两连接计算斜率,保留左右视图中斜率最接近的两对多边形作为目标特征.对每一个视图,定义两个相邻的多边形列表为Di和Dj,根据两个多边形的位置关系对多边形进行标号:规定多边形中心坐标横纵之和较小的为D1,另一个为D2,选出用于判别关键顶点的共边双框. (2)公共边顶点判别 选择两个多边形列表中对应像素值最接近的两点,其表征的是目标两个矩形的公共边顶点C1和C2,规定顶点横纵坐标之和较小的为C1,当坐标之和接近一致时优先像素坐标y轴较小的为C1,以此为约束使左右视图的顶点和多边形做到一一对应. (3)体对角顶点判别 本文提出了一种多边形体对角顶点判别方法,对于一个多边形S,从多边形的某一顶点px到对角顶点py经过的边的数量之和为定值N,将边的数量演化为边的权重,此时每条边的权重为定值1,针对特殊情况,边的权重值也有所变化,具体情况将在后续进一步分析.对不同顶点数的多边形设置不同起始值和起始顶点,根据边的权重减少步值,直到步值减少为0,到达对应的顶点.式(5)中wij表示从点px到点py经过的边的权重. (5) 确定公共边顶点C1和C2后,从顶点C2沿多边形D1顶点顺时针采用对角顶点判别法判断目标的上顶点Cup;从顶点C1沿多边形D2的顶点顺时针判别目标的下顶点Cdown.对一般情况而言,多边形Di和Dj的顶点个数都为4个,将对角顶点判别法中N设置为2,各个边的权重为1不做改变;而由于前期的形态学处理可能会导致目标的顶点处出现短边的干扰,导致多边形的顶点数ND大于4,此时将多边形中(ND-4)条最短的边的权重设置为0,在经过该段时默认为无效顶点,实现了特殊情况的判别,如图7所示. 图7 平面对应情况下的关键顶点判别Fig.7 Key vertex discrimination in the case of plane correspondence 当双目相机检测出的左右目视图只存在两个矩形平面,但只有一对平面对应,而另一对平面在空间中相互垂直时,此时平面中心点的斜率无法得到匹配,依据上述的判别方式则会出现图8所示的情况,该情况下的体对角顶点并不是一一对应的,也无法进行后续的判别. 图8 特殊情况顶点判别失败Fig.8 Special case vertex check failed 针对这一特殊情况,通过修改上述顶点与多边形的对应关系便可得到解决.先对左右视图中的某一组多边形修改判别规则,规则改变为:从顶点C1沿着多边形D1的顶点顺时针旋转得到上顶点Cup,从顶点C2沿着多边形D2的顶点顺时针旋转得到下顶点Cdown,另一视角的规则不做变化,判断当前的对应体对角顶点斜率是否一致,反之则修改另一视图下的判别规则,找到对应的体对角顶点.此时,对未修改规则视图下的顶点C1和C2,还需要沿公共面顺时针跨过一个顶点实现顶点C1和C2的对应.由于顶点顺序已按照顺时针方向排布,即找到C1和C2的下一个顶点坐标作为新的C1和C2.如图9所示,当两个视图中共边双框的中心点斜率不匹配时,修改某一视图中的判别规则,找到对应顶点斜率匹配的情况,进而实现4个关键顶点的判别. 图9 平面不对应情况下的关键顶点判别Fig.9 Key vertex discrimination in the case of plane mismatch 针对某视图只能检测出单个平面的特殊情况,单一的多边形信息无法满足对各个顶点的判别,也无法得到有效的对应点,对于上述情况,位姿参数的估计存在一定局限性.依据单个表面的信息可继续对目标规格做出判别,但存在误判的风险. 通过上述判别后得到了目标的对应顶点C1、C2、Cup和Cdown,基于视差原理可将上述4个顶点的三维坐标信息复原. 对于平行式双目相机,根据相似三角形的特点,在已知两相机基线长度B,焦距f和目标点在左右图像中的像素坐标(xl,yl)和(xr,yr),推导出目标点的三维坐标(Xw,Yw,Zw)如式(6)所示,(xl-xr)对应图像的视差,(x0,y0)为图像的中心点坐标 (6) 图10 立方星模型示意Fig.10 CubeSat model schematic (7) 目标的体中心坐标(X,Y,Z)可表示为式(8),也即平移矩阵T (8) 式中,(Cup(x),Cup(y),Cup(z))和(Cdown(x),Cdown(y),Cdown(z))分别对应点Cup和Cdown的三维坐标. 目标的旋转矩阵R可由式(9)中向量之间的叉乘确定 (9) 最后将旋转矩阵R转换为旋转角[α,β,γ].当β≠±90°时,根据式(10)解算出目标相对于相机的位姿;当β=±90°时,α=0°,γ由式(11)计算得到.式中,rij对应旋转矩阵中第i行、第j列的值. (10) (11) 通过上述计算,实现了目标的结构参数和位姿参数的估计. 将1U、2U和3U的立方星模型通过悬挂的方式放置于暗室中,使用Realsense D435i相机采集目标在不同姿态下的左右视图,图像分辨率为640*480,双目基线长度为50 mm,像素焦距为381 pixel.最终获得1U目标图像257对,2U目标图像291对,3U目标图像492对,选取部分图像如图11所示. 图11 部分采集图像Fig.11 Partially acquired image 首先验证本文边缘提取算法效果:将采集到的左右视图作为输入传入算法框架当中,验证本文算法框架对立方星结构参数判别的准确率,并采用通用的Sobel算子和Canny算法进行比对实验,准确率的计算公式为 (12) 其中,分母TP+TN+FP+FN表示数据集中所有数据的数量总和,TP表示正类被正确分类,TN表示负类被正确分类.由于数据集中无负类样本,将TN置为0,可简化为 (13) 由表1数据可知,Sobel算子由于其提取特征的能力有限,无法保证将边缘完整地提取,目标的表面纹理也会被算子无差别地提取出来,导致判别的准确率较低.传统Canny算法在设置好参数后通过双阈值法可避免过度的表面纹理提取,但使用时需要设置较多参数,通用性较弱.随着目标规格的增大,光照不均匀的现象加剧导致上述2个传统算法对目标模型判别的准确率骤减.而HED网络能够更好地提取出有效的边缘信息,并弱化了目标表面信息,达到66%以上的判别准确率.本文算法结合HED和形态学处理,将判别准确率提高了6%~10%,具有更为鲁棒的边缘提取效果,部分实现效果如图12所示. 表1 不同算法判别准确率Tab.1 Discriminant accuracy of different algorithms 图12 边缘提取效果对比Fig.12 Edge extraction effect comparison 为验证本文算法对空间场景中不同光照方向和目标不同表面材质的鲁棒性,设计比对实验如下: 将表面粗糙和表面光滑的立方星模型悬挂于暗室当中,设置外界光照条件为从左侧、后侧以及无光照3种情况,验证特征点提取的效果,实现效果如图13所示,可以看出该算法在不同光照场景和目标不同表面材质的情况下都能实现鲁棒性的关键顶点提取. 图13 不同光照方向和目标材质的关键顶点提取效果Fig.13 Key vertex extraction effects of different lighting directions and target materials 最后,设计平视和俯视的工况,验证本文位姿估计的效果和准确性,并与ICP算法[20]进行对比. ICP(iterative closest point)迭代最近点算法通过建立对应点之间的最近点集对求解刚体变化矩阵,目的是使得通过变换后所有点集对之间的欧氏距离最小,目标函数为 (14) 其中,RT对应配准两点云之间的旋转平移矩阵,pi和qi代表一组对应点集,pi对应场景目标点云,qi对应待配准模板点云.将模板点云通过旋转平移后与场景中的目标点云重合,计算出的模板点云旋转平移矩阵即为目标相对于相机中心的位姿. ICP能够通过点云之间的变换关系计算出目标的位姿,但应用于空间探测的双目相机通常并不具备生成点云的能力,且点云之间的位置解算过程也会带来较大的计算量,在空间应用场景中存在局限性.本文采用的相机具有生成场景点云的能力,因此可以将ICP算法作为本文算法的结果参照,进而验证本文位姿结果的有效性. 工况1为平视,相机平视目标,双目连线水平,光轴水平,验证1U立方星目标与Z轴距离从30~70 cm变化下的位姿结果;工况2为俯视,相机俯视目标,双目连线水平,光轴倾斜,验证Z轴距离从40~70 cm变化下的位姿结果.平视和俯视状态下各参数均值与标准差结果如表2~3所示,平视和俯视状态下各参数与ICP精配准结果差绝对值如表4~5所示. 表2 平视状态各参数均值与标准差Tab.2 Mean value and standard deviation of each parameter in the head-up state 表3 俯视状态各参数均值与标准差Tab.3 Mean value and standard deviation of each parameter in overlooking state 表4 平视状态各参数与ICP精配准结果差绝对值Tab.4 The absolute difference between the head-up state parameters and ICP registration results 表5 俯视状态各参数与ICP精配准结果差绝对值Tab.5 The absolute difference between overlooking state parameters and ICP registration results 由表2~5可以看出,在平视和俯视工况下,Z轴的位置信息精度较高,但随着距离的增加,其他参数的标准差逐渐增大,这是由于随着目标远离相机,目标像素点的较小偏差会带来更大波动,但均值的一致性得以保证;将上述位姿估计方法与ICP精配准方法的结果进行对比,并将ICP精配准方法的结果作为基准对方法位姿估计准确性进行验证,旋转角结果最大差值为4.38°,距离最大差值为1.2 cm,能够满足位姿估计的需求. 本文针对立方星检测与位姿估计中的缺陷与不足,提出HED网络结合二值化形态学处理的方法实现了鲁棒性的边缘提取,还提出一套共边双框关键顶点判别算法,实现了对立方星规格判别和位姿估计.对比其他边缘提取算法实现更为鲁棒的提取效果,判别规格准确率提升4%~10%.位姿结果相比ICP精配准方法位姿最大差值4.38°,距离最大差值1.2 cm,为空间非合作目标立方星的检测跟踪技术路线提供了新思路. 但双目视觉探测效果受基线长度影响,距离较短,近距离也存在遮挡现象,后续可以考虑实现多双目联合探测以适应更多检测场景.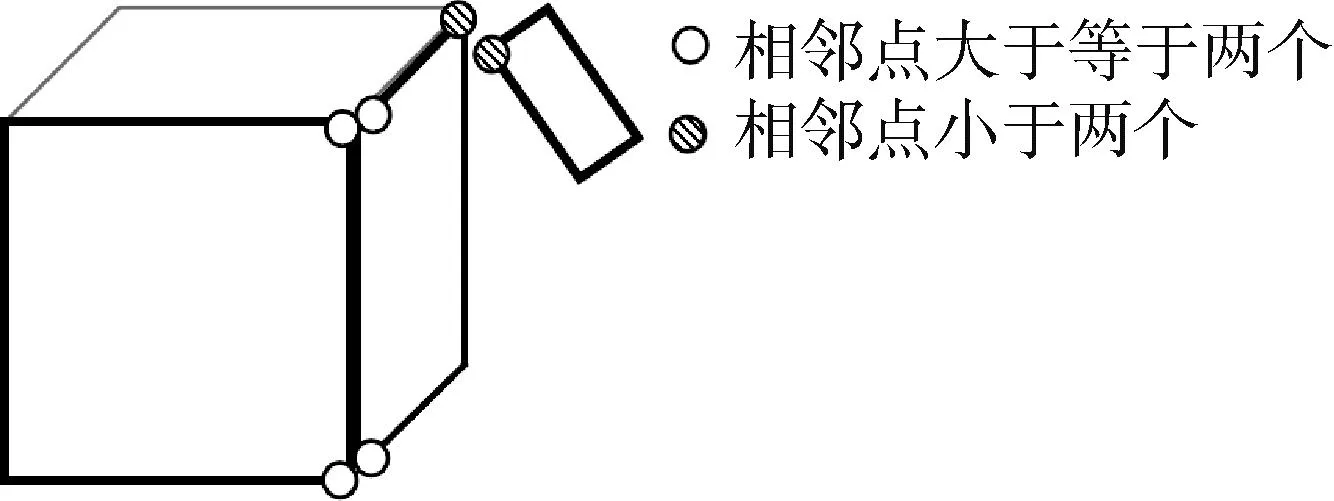
1.3 目标关键顶点判别

1.4 目标规格判别与位姿估计
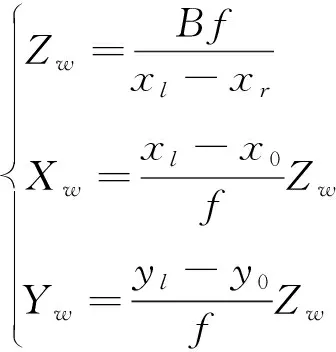
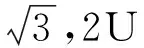
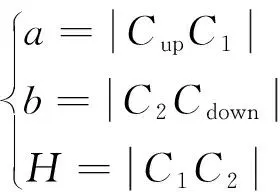
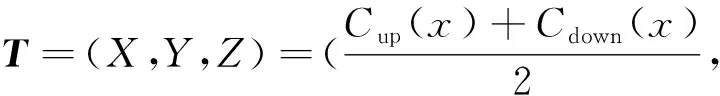
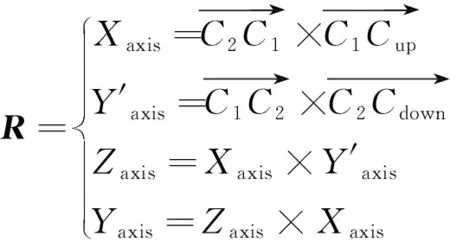
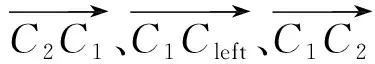
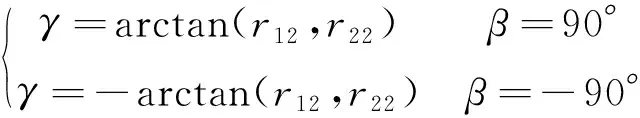
2 算法验证
2.1 数据采集

2.2 边缘提取实验验证


2.3 位姿估计实验验证




3 结 论
