深度学习视域下一道电磁感应高考题的探讨
2023-12-30徐富锋
徐富锋






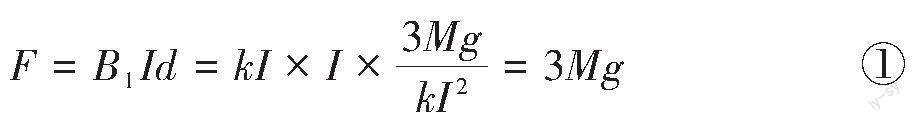

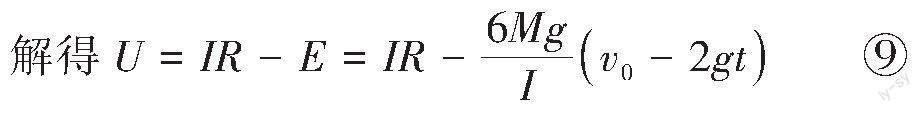

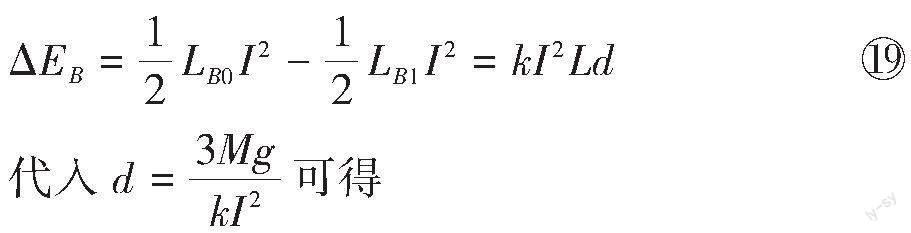
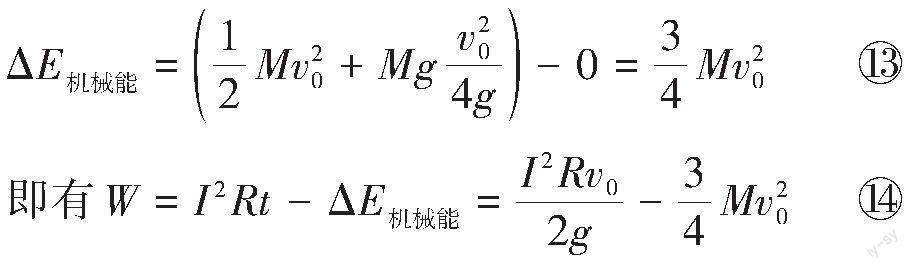
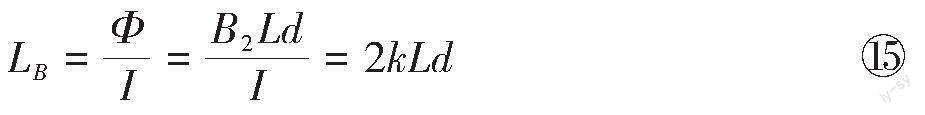


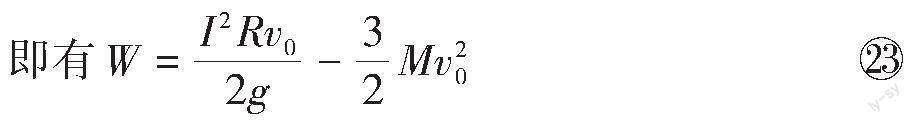



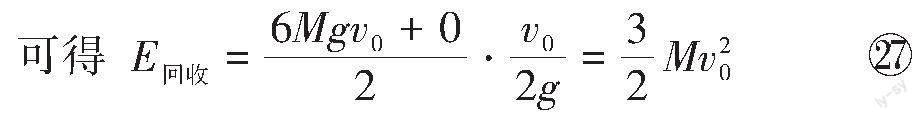
[摘 要]通过分析探讨2023年浙江6月选考物理第19题的不同解法及其矛盾,引导学生领悟磁能的存在并了解其计算方法。在深度学习理论的指引下,通过提出问题、初步探讨、深入探究、迁移运用、拓展思考等过程,引导学生经历分析、评价、创造等思维过程,使得探讨层层递进、不断深入。通过深入探讨,明确了问题的关键所在,并找到了问题的解决办法,培养了学生的批判性思维和辩证思维。
[关键词]深度学习;电磁感应;磁能;矛盾
[中图分类号] G633.7 [文献标识码] A [文章编号] 1674-6058(2023)26-0035-04
深度学习是指在教师的引领下,学生围绕具有挑战性的学习主题,全身心投入、积极参与、体验成功、获得发展的有意义的学习。它是我国全面深化课程改革、落实核心素养的重要路径。因此,教师在高中物理教学中要以学生为中心,将学习探索的主动权交给学生,引导学生开展形式多样的探究活动,从而促进学生自主建构知识,独立思考和解决问题,使学生真正实现深度学习。
在深度学习理论的指引下,笔者在讲解2023年浙江6月选考物理第19题时引导学生从不同角度思考与解决问题,化解答案不一致的矛盾。同时,引导学生进一步思考题目条件设置的严谨性和解题中遇到的问题,以此激励学生深入思考问题,进而探讨问题的解决方法。这样通过思考与解决问题,学生的批判性思维和辩证思维得到了很好的发展。
一、真题呈现
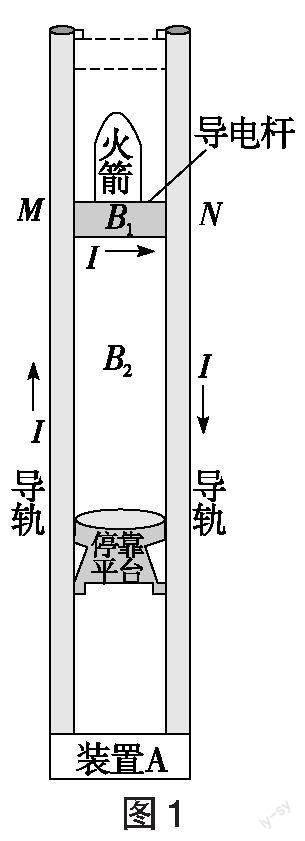
某兴趣小组设计了一种火箭停落装置,简化原理如图1所示,它由两根竖直导轨、承载火箭装置(简化为与火箭绝缘的导电杆[MN])和装置[A]组成,并形成闭合回路。装置[A]能自动调节其输出电压确保回路电流[I]恒定,方向如图所示。导轨长度远大于导轨间距,不论导电杆运动到什么位置,电流[I]在导电杆以上空间产生的磁场近似为零;在导电杆所在处产生的磁场近似为匀强磁场,大小[B1=kI](其中[k] 为常量),方向垂直导轨平面向里;在导电杆以下的两导轨间产生的磁场近似为匀强磁场,大小[B2=
(1)求导电杆所受安培力的大小[F]和运动的距离[L];
(2)求回路感应电动势[E]与运动时间[t]的关系;
(3)求装置[A]输出电压[U]与运动时间[t]的关系和输出的能量[W];
(4)若[R]的阻值视为零,装置[A]用于回收能量,给出装置[A]可回收能量的来源和大小。
二、基本问题解答
(1)导电杆所受安培力的大小为:
对导电杆,由牛顿第二定律可得
[3Mg-Mg=Ma] ②
解得 [a=2g] ③
根据运动学公式可得 [02-v20=2(-2g)L] ④
评析:第(1)问和第(2)问以安培力的计算、牛顿第二定律和法拉第电磁感应定律的基本运用为背景考查学生在运用物理知识分析与解决综合问题的能力,设问具有基础性和综合性。
三、提出疑问
对于第(3)问,从不同角度去思考,会得到截然不同的结果。
解法1:根据右手定则和闭合电路欧姆定律可得 [U+E=IR] ⑧
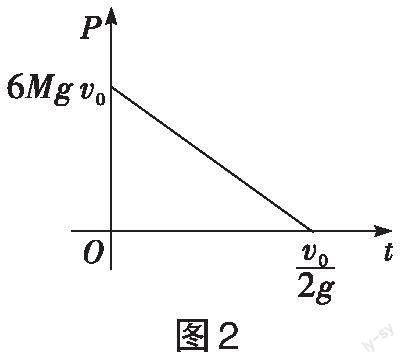
装置A输出的功率为
解法2:从能量守恒观出发解题。电源提供的能量、导电杆与火箭减少的机械能都转化为回路产生的焦耳热。可得:
[W+ΔE机械能=I2Rt] 12
全过程减少的机械能为
疑问:解法1和解法2分别从不同的角度出发解决问题得到了不同的结果。究竟是什么原因导致的呢?到底哪一种解法的结果是正确的呢?
四、初步探讨
分析第(3)问两种解法的异同发现,解法1用到了闭合电路欧姆定律、电源功率计算式和功与功率的关系式;解法2用到了能量守恒定律和机械能表达式。以上提到的定律和表达式对本问题都适用,方法上没有问题。解法1从功率计算式[P=UI]出发得到[P与t]的关系式,由于功率随时间线性变化,因此可用功率的平均值计算装置[A]输出的能量W。该解法的逻辑思路没有问题,可判定其得到的结果是正确的。解法2从能量守恒的角度看待问题,考虑了电源提供的能量、导电杆与火箭减少的机械能以及回路产生的焦耳热。那么整个装置系统中,仅仅考虑这三类能量全面吗?回顾高中物理必修第三册磁场的相关章节可知,运动的电荷形成的电流周围会产生磁场,即回路的电流会产生磁场。而磁场也具有相应的磁能。分析11和14式可知,解法2所得的结果比解法1所得的结果要大,显然是忽略了某一种能量而导致的错误。通过分析可知,解法2是忽略了磁能而导致的错误。那么,我们能否计算出磁能的大小,从而使得两种解法得到的结果一致呢?
五、深入探究
从定量计算的角度看,设整个回路的自感系数为[LB],此时回路中导轨有电流的长度為[L]。由 [Φ=B2Ld] 可得自感系数为
磁场能量为
回路初状态的自感系数为
[LB0=2kd(L0+L)] 17
回路末状态的自感系数为
[LB1=2kdL0] 18
则初末状态的磁场能减少量为
[ΔEB=3MgL] 20
因此装置[A]输出的能量为
[W=Q-WA-ΔEB] 22
Q为焦耳热,WA为克服安培力所做的功
此时得到了与解法1相同的结果。这里的定量计算中运用到了自感系数的定义式和磁能的表达式,超出了高中物理知识范围,但能为强基优生进一步深入思考问题和一线教师解答学生疑惑提供适当的参考。
六、迁移运用
对于第(4)问,可分别从三种视角切入思考与解决问题,从而训练学生运用多种物理规律思考与解决问题的综合思维能力,加深学生对物理规律与概念的理解,促使学生的思维从浅层走向高阶,实现发展学生高阶思维的目标。
解法1:若[R]的阻值视为零,装置[A]用于回收能量,可得
负号表示装置[A]回收能量,则有
装置A回收的能量来源于火箭和导电杆减少的机械能和全过程减少的磁场能。
以上的解答过程是对处理好上面的矛盾后所得到的结果的直接运用。那么在没有处理好矛盾的情况下,即本题回避运用23 式这一表达式的情况下,该如何解答呢?其实,可以类比第(3)问解法1的做法,运用功率的计算式来求解,这样可以回避之前的矛盾。
解法2:导电杆向下运动的过程使得回路的磁通量逐渐减少而产生感应电动势,当回路产生的感应电动势提供的电流大于[I]时,装置[A]处于充电状态,可得[E-U=IR] ,于是有 [U=E-IR] ,当[R=0] 时,有[U=E]。
由于装置[A]的作用是保持电流大小和方向不变,因而其产生的磁场大小和方向不变,即安培力大小和方向不变,从而火箭和导电杆做匀减速运动的加速度不变。
给装置[A]充电的功率为
解法3:
我们根据能量守恒定律可知,装置[A]回收的能量等于全过程减少的机械能和减少的磁能之和,由[⑬]和 21 式可得
评析:从三种不同的视角思考可得出三种不同的解法。解法1直接运用前文中输出能量[W]的表达式,然后令表达式中的[R=0],从而得出答案,较为简单,很容易得到正确答案。解法2则是类比第(3)问解法1的思路与处理方法进行求解,同样可以得到正确答案,同时回避了磁能矛盾的计算。解法3从能量守恒的视角将机械能和磁能的减少量相加得到最终答案。从上述讨论可以看出,从不同角度切入思考与解决问题,能加深学生对物理规律与结论的理解;开展多角度思考问题的训练,有助于增加学生思考问题的思维深度。
七、拓展思考
为培养学生的批判性思维和辩证思维,促进学生高阶思维的发展,教师可以引导学生探讨题目条件设置的合理性,以及如何修正题干以提高试题命制的严谨性与科学性。此外,因为该装置源于生活生产,为加深学生对该装置工作机制的理解,教师可以引导学生分析装置运行过程中感应电动势的具体产生过程。
问题1:为什么导电杆处的磁场与导电杆下方的磁场成两倍关系?
题目中给出“在导电杆所在处产生的磁场近似为匀强磁场,大小为[B1=kI](其中[k] 为常量),方向垂直导轨平面向里;在导电杆以下的两导轨间产生的磁场近似为匀强磁场,大小为[B2=2kI],方向与[B1]相同”这一近似磁场大小关系条件。
对于题目中的假设条件,我们可以这么理解:
由题意可知,导轨长度远大于导轨间距,因此可认为左右均为无限长的电路导线,则两导轨间可近似认为是磁感应强度为[B]的匀强磁场。在导电
当导电杆距离停靠平台较远时,满足可将某一位置处两侧导轨电流视为无限长的合理区域较多,因而题目条件成立的合理性较强。当导电杆不断靠近停靠平台时,满足合理位置条件的区域变少,因而题目条件成立的合理性降低。因此,该题的导电杆处和其下方的磁感应强度关系是准确性比较低的近似,严谨性不够。要使題目条件保持较好的准确性和科学性,应给题目加上一个说明条件:停靠平台到装置[A]的距离远大于两导轨的间距。
问题2:为什么安培力公式、感应电动势公式中的磁感应强度用不同的值?
由安培力公式[F=BId] 可知,公式中的磁感应强度应该是导电杆所在位置的磁感应强度[B1]。那么,在计算感应电动势时,运用公式[E=B1dv]是否正确呢?
做法一:
当导电杆的速度为[v]时,回路的磁通量为
[Φ=B2L'd] 29
上式中,[L'] 为导电杆距离装置[A]的距离。由法拉第电磁感应定律可知,此时产生的感应电动势为
做法二:
由公式[E=Bdv]可知,磁场强度[B]应该是切割部分的磁场的强度,故有
[E=B1dv] 31
评析:做法二显然是错误的。这种做法的错误之处在于没有考虑磁场是变化的,即导电杆处与其下方的磁感应强度大小不同,为变化磁场,因此单纯用动生电动势来计算是不合理的。我们之前运用动生电动势公式求解电动势时所遇到的均是匀强磁场。题目中的情境属于是磁通量和磁感应强度同时变化的磁感应类问题,不能做单一变量处理,比较复杂,需要慎重思考。运用法拉第电磁感应定律解决问题时,我们需要考虑闭合区域的磁通量大小,而不必考虑边界处磁感应强度微乎其微的影响。题目中导电杆处的磁感应强度与其他区域的磁感应强度大小不同,便于利用法拉第电磁感应定律解答,从而规避运用动生电动势计算出现的错误。
本文通过分析不同解法出现的矛盾,让学生领悟磁能的存在并了解其计算方法,同时也让广大教师产生电磁感应问题中磁能不可忽略的认识。此外,通过多角度引导学生思考物理问题强化思维训练,有助于发展学生的高阶思维,培养学生的关键能力。文中对题目条件设置合理性的探讨,有助于培养学生的批判性思维,引领学生思维发展和讨论层层深入,进而达到发展学生高阶思维的目标。文中各个部分的探讨与解决问题的过程中蕴含评价、分析、应用、创造等高阶思维,有助于培养学生的科学思维,落实物理学科核心素养的培养目标。
[ 参 考 文 献 ]
[1] 刘月霞,郭华.深度学习:走向核心素养[M].北京:教育科学出版社,2018.
[2] 李万杰.深度学习视域下一道椭圆摆问题的探讨[J].中学物理教学参考,2022(31):17-21.
[3] 梁灿彬,秦光戎,梁竹健.普通物理学教程:电磁学[M].4版.北京:高等教育出版社,2018.
