基于BO-GRU神经网络的锂离子电池剩余使用寿命预测*

□ 安元超 □ 张岳君 □ 林文文 □ 沈伟豪

1.宁波大学 机械工程与力学学院 浙江宁波 315211 2.浙江工商职业技术学院 机电工程学院 浙江宁波 315699

1 研究背景

锂离子电池具有能量密度大、功率密度高、使用寿命长、自放电低且无记忆效应等优点,目前已经广泛应用于各类储能装备,尤其是在新能源汽车中,得到了广泛应用。锂离子电池在使用过程中,电池容量会不断衰减。有多个特征能够用于衡量电池容量的衰减,电池最大可用容量下降至初始容量值的80%,就可以认为电池失效[1]。锂离子电池剩余使用寿命指锂离子电池最大可用容量从当前时刻衰减到失效阈值所经历的充放电循环周期数[2]。

目前,国内外关于锂离子电池剩余使用寿命预测方法的研究中,最多的是使用基于数据驱动的方法。基于数据驱动的方法不需要对锂离子电池内部机理进行深刻分析,而是通过挖掘出锂离子电池数据的变化规律,建立预测模型,就可以得到比较准确的锂离子电池剩余使用寿命。

常用的基于数据驱动的方法有支持向量机[3]、相关向量机[4]、极限学习机[5]、人工神经网络[6]等。人工神经网络的改进网络在锂离子电池剩余使用寿命预测研究中具有很好的应用,如循环神经网络[7]、长短期记忆神经网络[8]、门控循环单元神经网络[9]等。其中,支持向量机、相关向量机、极限学习机等属于浅层学习方法,一般用于处理小规模预测问题,而循环神经网络、长短期记忆神经网络、门控循环单元神经网络属于深度学习方法,具有更强的处理复杂非线性大数据的能力,适合处理锂离子电池的非线性退化问题。

锂离子电池在退化过程中会出现不同程度的容量回升现象[10],这种容量回升会导致模型的预测准确性降低,对此,不少学者考虑融合其它算法来提高模型的精度。Ren Lei等[11]考虑锂离子电池在实际使用时会受到外部因素的影响,以及标准放电得到的退化数据量的有限性,提出一种Auto-卷积神经网络-长短期记忆神经网络方法,预测锂离子电池的剩余使用寿命。Pan Dawei等[12]提出一种基于长短期记忆神经网络融合粒子滤波的预测锂离子电池不同工况下剩余使用寿命的方法。Kara[13]提出一种卷积神经网络-长短期记忆神经网络-粒子群优化方法,预测锂离子电池的剩余使用寿命。然后,融合型方法虽然能够在一定程度上提高单一模型的预测精度,但是依然存在建模困难、融合不确定、模型参数调节困难等问题。

笔者在以上各研究的基础上,提出一种基于贝叶斯优化-门控循环单元神经网络的锂离子电池剩余使用寿命预测方法。这一方法通过提取循环数作为新特征,与对应的容量特征进行融合,来完成特征数据的升维;采用滑动窗口方法,通过分割特征数据集,完成数据集的扩充;引入随机失活技术,搭建神经网络模型,采用贝叶斯方法优化模型,进而实现对锂离子电池剩余使用寿命的准确预测。

2 试验数据

2.1 数据获取

笔者采用的数据为美国国家航空航天局实验室的B5号、B6号、B18号电池容量数据与自主测试的1号、2号电池容量数据。为了验证模型在不同数据集上的表现,自主测试的电池型号、试验条件、测试环境设置与美国国家航空航天局数据不同。自主测试的电池为INR1865025P三元锂离子电池。

充电方案如下:以4 A恒流方式对锂离子电池充电至电压为4.2 V,然后以4.2 V恒压方式对锂离子电池充电至容量为0.25 Ah,停止充电,静置10 min。在充电过程中,每隔1 min收集一次电流、电压等数据。在充电结束的静置过程中,每隔3 s收集一次电压等数据。

放电方案如下:以20 A的放电电流对锂离子电池放电至电压为2.5 V,停止放电,静置30 min。在放电过程中,每隔1 s收集一次电流、电压等数据。在放电结束的静置过程中,每隔2 min收集一次电压等数据。

上述充电、放电各进行一次为一次完整的充放电,通过重复充放电进行循环测试,收集测试数据。

2.2 数据处理

在锂离子电池剩余使用寿命预测中,大多数学者会将容量作为直接特征输入至网络中,进行未来的容量的预测,输入的特征只有一维特征。笔者考虑将每个容量点所对应的循环数作为第二个特征,与容量特征组合为二维特征。考虑到两个特征的量纲不同,采用Z分数标准化公式对数据进行标准化。

(1)

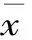
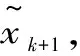
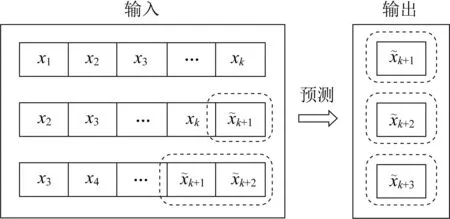
图1 滑动窗口法预测

3 预测原理

3.1 预测框架

基于贝叶斯优化-门控循环单元神经网络对锂离子电池剩余使用寿命进行预测,预测框架如图2所示。

图2 预测框架

3.2 门控循环单元神经网络

传统的循环神经网络在解决时间序列问题时容易出现梯度消失、梯度爆炸的问题,一旦出现这种问题,就很难学习到新的信息,因此需要对循环神经网络进行改进。循环神经网络常见的变体有长短期记忆神经网络、门控循环单元神经网络。门控循环单元神经网络是在标准的长短期记忆神经网络基础上改进的,主要将长短期记忆神经网络中的遗忘门和输入门改为一个更新门,从而减少模型参数,加快训练速度。门控循环单元神经网络结构如图3所示。图3中,zt为更新门,rt为重置门,门控循环单元神经网络通过这两个门实现对信息的传输。

图3 门控循环单元神经网络结构

对门控循环单元神经网络结构中的输入、输出进行计算,为

zt=σ(Wz·[ht-1,xt])

(2)

rt=σ(Wr·[ht-1,xt])

(3)

(4)

(5)

其中,遗忘门和输入门合并之后,zt是需要记住的信息,忘记信息则通过1-zt实现。

3.3 随机失活

随机失活指在深度学习中,通过以一定的概率随机丢弃一些隐含层的神经元,切断神经元与前后神经元之间的信息传递,使其暂时失去活性,目的是防止神经网络对训练数据的过拟合而失去对未来预测的泛化能力。

在门控循环单元神经网络训练过程中,加入随机失活,表现为在每一次迭代预测时都会根据一定的概率随机选中一些神经元,使其暂时失活,失活的神经元不再参与前向和后向的传播计算。

3.4 贝叶斯优化

对深度学习模型进行参数耦合较为复杂,在依靠人工经验调节的基础上,确定参数范围,加入参数优化算法,能够进一步寻找到最优的模型参数。

贝叶斯优化是机器学习常用的参数寻优算法,适合在深度学习中复杂的神经网络参数调节。笔者采用贝叶斯优化来确定最优参数组合,贝叶斯优化结果见表1。

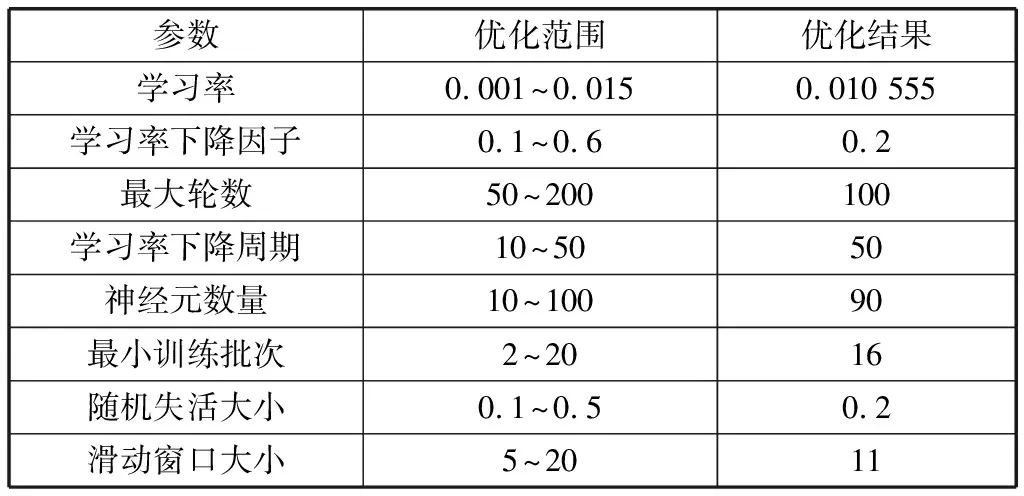
表1 贝叶斯优化结果

4 评价指标

预测锂离子电池的剩余使用寿命,指从预测起点EOP开始预测,直到寿命结束点EOL期间所历经的循环次数。

为了定量评价预测性能,采用三种评价指标,分别为绝对误差RULae、相对误差RULre和均方根误差RMSE,计算式为:

RULae=|EOP-EOL|

(6)

RULre=RULae/EOL×100%

(7)

(8)

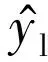
5 预测结果分析

5.1 贝叶斯优化

初始化长短期记忆神经网络参数、门控循环单元神经网络参数,分别开展训练,对两种锂离子电池分别进行剩余使用寿命预测,再根据表1参数重新设置长短期记忆神经网络参数、门控循环单元神经网络参数,分别进行训练、预测。

两种锂离子电池的剩余使用寿命预测结果如图4、图5、表2所示。

表2 贝叶斯优化预测结果

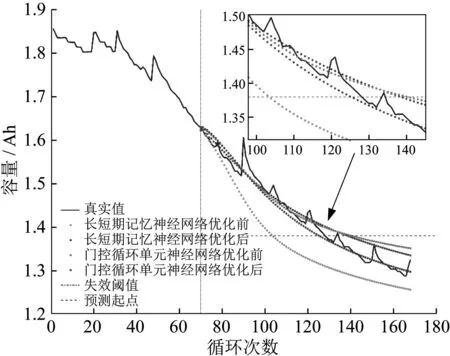
图4 B5号电池剩余使用寿命预测结果

图5 1号电池剩余使用寿命预测结果

由表2可知,对于美国国家航空航天局实验室数据,贝叶斯优化后长短期记忆神经网络、门控循环单元神经网络的平均相对误差减小约13.5个百分点,对于自主测试数据,平均相对误差减小约17.7个百分点。门控循环单元神经网络在两类数据上的平均相对误差约为2.5%,低于长短期记忆神经网络的6.6%,由此证明贝叶斯优化-门控循环单元神经网络的优越性。

5.2 随机失活

对于长短期记忆神经网络和门控循环单元神经网络,在不同起点下选择是否加入随机失活,对锂离子电池剩余使用寿命进行行预测。

美国国家航空航天局实验室数据电池预测结果相似,B5号电池不同起点剩余使用寿命预测结果如图6所示,B5号电池预测绝对误差如图7所示。1号电池以90为起点剩余使用寿命预测结果如图8所示。锂离子电池剩余使用寿命预测结果对比见表3。

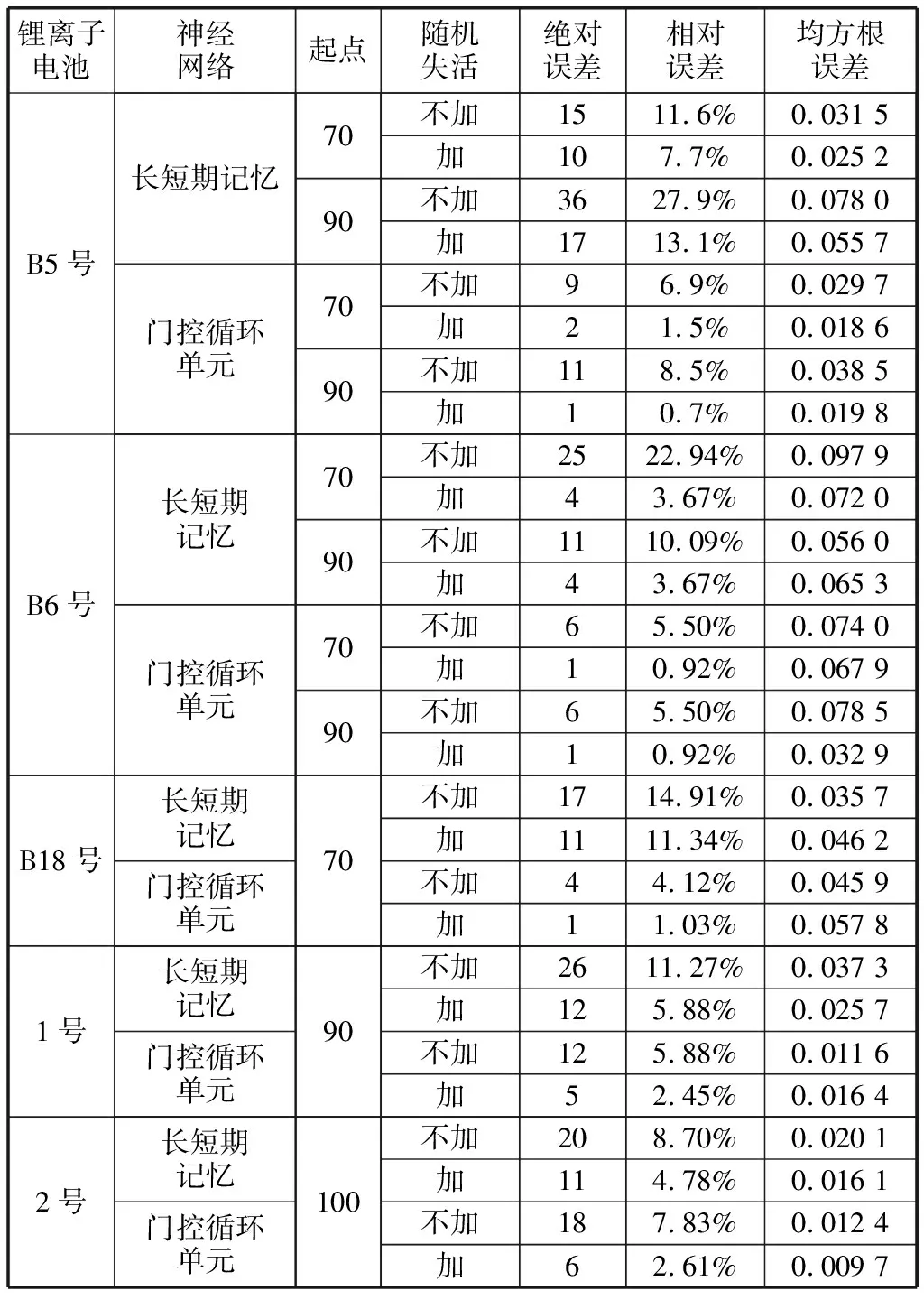
表3 锂离子电池剩余使用寿命预测结果对比

图6 B5号电池不同起点剩余使用寿命预测结果

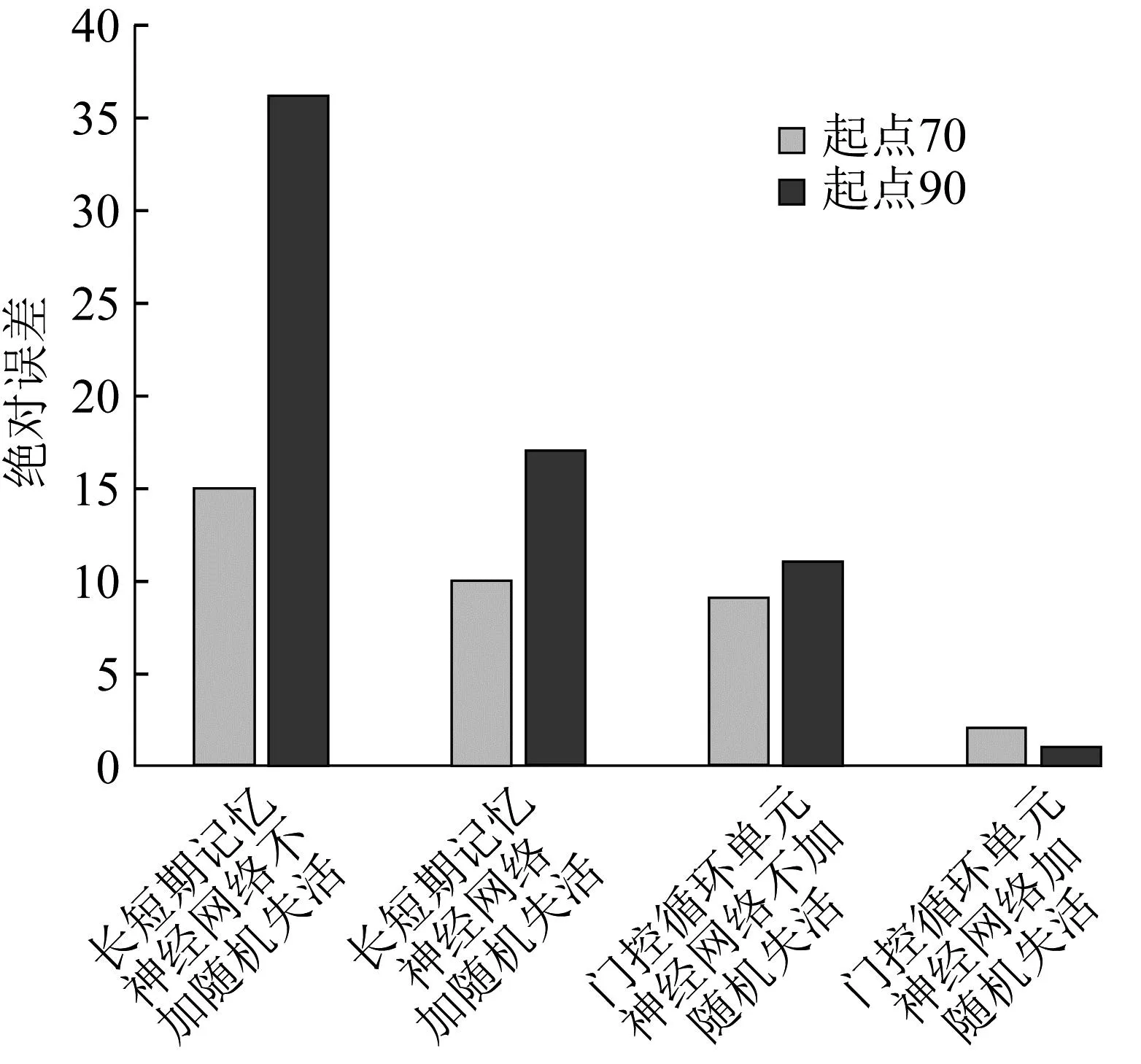
图7 B5号电池预测绝对误差

图8 1号电池以90为起点剩余使用寿命预测结果

由图7可知,长短期记忆神经网络以70为起点的锂离子电池剩余使用寿命预测误差小于以90为起点,原因在于第90周期出现了较大的容量回升,导致预测精度降低。加入随机失活后,两种神经网络的预测精度大幅提高。

通过以上试验可见,加入随机失活后门控循环单元神经网络对于美国国家航空航天局实验室数据的平均相对误差稳定在1%,对于自主测试数据的平均相对误差约为2.5%,由此通过两种锂离子电池验证了贝叶斯优化-门控循环单元神经网络具有较高的剩余使用寿命预测精度,并且在不同锂离子电池中具有一定的通用性。

6 结束语

笔者提出一种基于贝叶斯优化-门控循环单元神经网络的锂离子电池剩余使用寿命预测方法,通过提取循环数与对应的容量融合作为新特征,采用滑动窗口方法分割特征数据集,构建门控循环单元神经网络,加入随机失活,采用贝叶斯优化来优化门控循环单元神经网络参数,进而对锂离子电池剩余使用寿命进行预测。在美国国家航空航天局实验室数据和自主测试数据上进行试验验证,相对误差均小于3%,平均均方根误差小于0.027,能够实现对锂离子电池剩余使用寿命的准确预测,具有一定的通用性。