环形流道内扰流柱参数优化的模拟分析
2023-12-29王风录
王风录 虞 斌 吕 林 许 蕾
(南京工业大学机械与动力工程学院)
套管式热交换器[1]被广泛应用于石油、化工等行业的生产过程中。 相较于其他形式的换热器,套管式热交换器具有结构简单、换热面积增减自如、传热效能高及纯逆流传热等优点。 在设计过程中基于传热介质物性的不同,可使用多种被动方式提高套管结构的传热效率,如改变套管的形 状[2,3],加装 翅片[4~7]、肋槽[8,9]、扰流 柱[10~12]及内插物[13,14]等,通过破坏或消除流体壁面 的边界层、产生二次流促进流体的混合、改变流场和温度场的分布特性以及增大换热面积等方式,达到强化换热的效果。
张延静等指出,钉头管换热器具有良好的强化传热效果,与光管相比,其总传热系数可提高约88%[15]。钉头结构既增大了传热面积,也使套管环形流道中的流体更易形成湍流,能够进一步强化换热。 ZHANG L等指出,安装扰流柱的螺旋流道具有更高的流速,速度分量的功率谱范围也更宽[16],扰流柱能够显著增加湍流的生成。 虞斌等研究的一套高温高含尘炉气急冷器系统中采用了套管结构[17]。设备中的套管结构可将1 500 ℃的高温炉气在极短时间 (0.01 s) 内急速冷却到750~900 ℃,过程中可获取大量热能。 在内、外套管之间须设置支撑结构, 保证总长度约12.5 m的内管在压力和温度的作用下,具有足够的刚度,不致发生屈曲失效等;同时,套管间的支撑结构也能够起到强化传热的效果。 笔者在之前的研究基础上, 在套管的环形流道内周期性地布置不同参数的扰流柱, 并采用正交试验结合数值模拟的方法对其进行优化,使之获得更好的强化传热效果。
1 模型描述
1.1 模型建立与基本假设
高温高尘炉气急冷器的结构如图1所示,中段部分为套管结构,取该部分作为研究对象。 套管的内外管长度均为7.5 m,外管尺寸为φ89 mm×6 mm,内管尺寸为φ62 mm×5 mm;扰流柱的截面为椭圆形,短轴长度为a,长轴长度为b,扭转角为α,相邻两环扰流柱的圆周差角为β,扰流柱数量为每环m个,如图2所示。为得到更好的模拟结果,在套管的出入口处均同时延长一段距离。 套管内管中的介质为高温烟气,密度0.474 kg/m3[18];环形流道中的介质为软水,密度951 kg/m3。 套管材料为15CrMo。

图2 套管和扰流柱局部结构示意图
对模型的数值计算做如下假设:
a.物理模型为三维结构,最外层壁面不与环境发生热交换;
b.忽略重力对流场的影响;
c.流体为不可压缩流体,是稳态的、充分发展的湍流。
1.2 边界条件与数值处理方法
边界条件:内管的进口为速度入口62 m/s,温度1 500 ℃; 环形流道的进口为速度入口0.6 m/s,温度110 ℃; 内管与环形流道的出口均采用压力出口,分别为0.3、4.0 MPa。 所有壁面均采用无滑移边界条件;固-液交界壁面设置为耦合壁面;最外侧壁面采用绝热壁面, 不与外界发生热量交换。
数值处理方法:
a.采用双精度求解器, 选取RNG k-ε方程模型,并对壁面采用增强壁面函数处理;
b.由于内管介质是高温烟气,套管的换热除了对流传热外, 还必须考虑烟气的辐射换热,因此激活P-1辐射模型;
c.压力和速度耦合采用Simple算法,动量、能量、湍动能和湍流耗散率离散均采用二阶迎风格式,以提高精度。
2 正交试验及分析
2.1 评价指标
努塞尔数Nu和阻力系数f的定义如下:
式中 de——当量直径;
h——对流换热系数;
L——有效长度;
u——流场平均流速;
ΔP——进出口压降。
为了评价环形流道内设置不同尺寸参数扰流柱的综合强化传热性能,引入工程上普遍使用的综合评价指标(PEC),其计算式为:
式中 f——有扰流柱的套管的阻力系数;
f0——无扰流柱的套管的阻力系数;
Nu——有扰流柱的套管的努塞尔数;
Nu0——无扰流柱的套管的努塞尔数。
2.2 正交试验
正交试验可以在短时间内用较少的试验次数确定不同因素的最佳匹配关系。 模拟因素包括扰流柱椭圆截面的短轴长度a、长短轴之比c、扰流柱的环向布置个数m、轴向布置环数n、相邻两环的圆周差角β和扰流柱的扭转角α,共6个因素,目标函数是Nu、f和PEC。 在不考虑交互作用的情况下,本次研究使用正交表L18(36)。
2.3 网格无关性验证
对模型进行网格无关性计算分析,选取正交试验中第2组试验, 以环形流道的压降作为观测变量,其网格无关性分析规律如图3所示。 网格数量达到60万之后,压降变化趋于平缓,故选取70~80万网格作为计算网格。

图3 计算网格独立性验证
2.4 试验结果与极差分析
正交试验选取的因素、水平、方案和计算结果见表1。采用极差分析法对结果进行分析。极差分析法是计算相同试验因素在不同水平下的平均值,通过一组平均值中的极大值与极小值之间差值的大小,可以直观地表现出各个因素影响目标函数的影响程度。 差值越大,说明该因素对目标函数的影响程度越大。

表1 扰流柱正交试验表及数值计算结果
基于正交试验结果分别对目标函数Nu、f和PEC进行极差分析。
基于极差分析结果得到各因素水平对Nu、f和PEC的影响趋势如图4所示。

图4 各因素水平对Nu、f和PEC的影响趋势
因素水平对Nu的影响见表2,分析表2中的数据可知, 各因素水平对Nu影响的主次顺序为:扰流柱的短轴长度a>扭转角α>相邻环圆周差角β>长短轴之比c>轴向环数n>环向个数m。 图4中,随着扰流柱短轴长度的增加,Nu显著上升。 Nu对于长短轴之比、 环向个数和轴向环数3个因素的水平变化相对不敏感。 相邻环圆周差角和扭转角对Nu的影响受到多因素耦合作用,变化规律并不是随着水平变化而单纯的增加或减少。若只考虑Nu这一个指标, 最优的水平组合是A3B3C3D3E3F3,即为正交试验中的第18 组试验, 此时PEC 值为1.633。
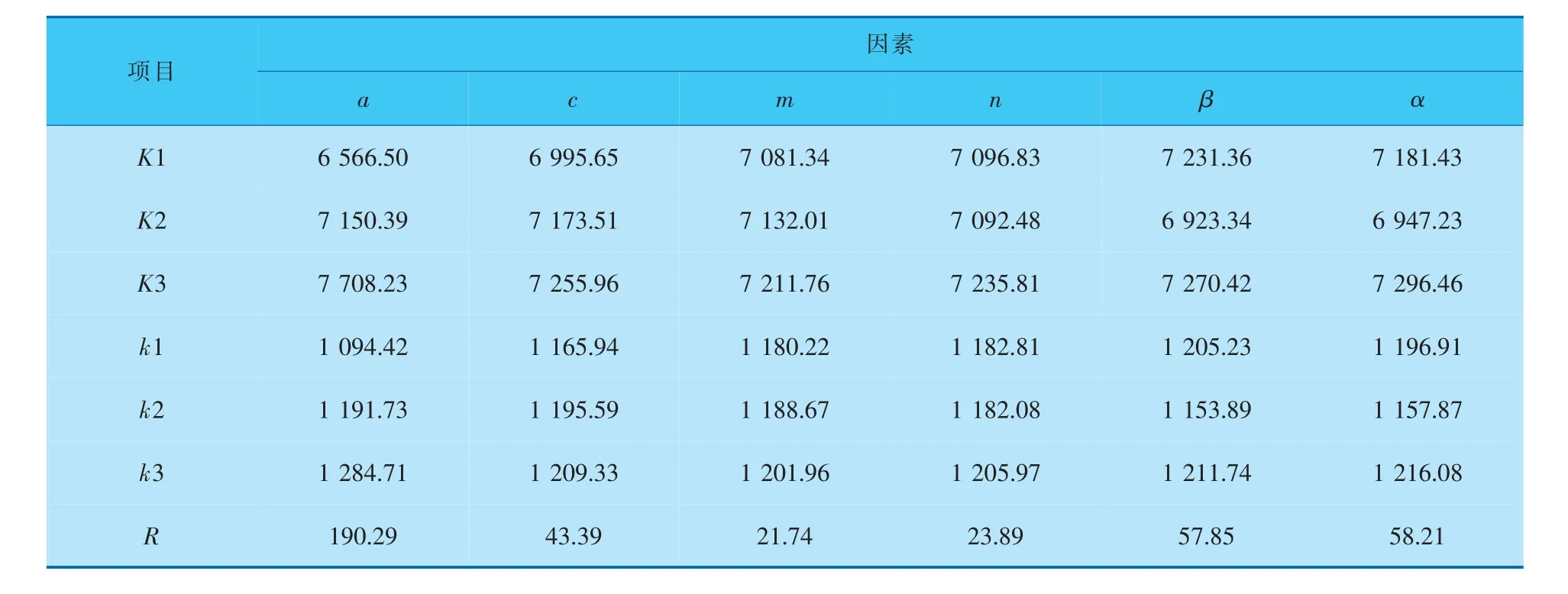
表2 Nu极差分析表
因素水平对阻力系数f的影响见表3,分析表3中的数据可知, 各因素水平对f影响的主次顺序为:扰流柱相邻环圆周差角β>环向个数m>短轴长度a>轴向环数n>长短轴之比c>扭转角α。 图4中,f随着短轴长度的增加、环向个数和轴向环数的增多显著上升; 相邻环圆周差角的增加使f显著下降。f对于长短轴之比和扭转角的水平变化相对不敏感。 若只考虑f这一个指标,最优的水平组合为A1B2C1D1E3F1,经再次建模并数值模拟验证其PEC值为1.50。
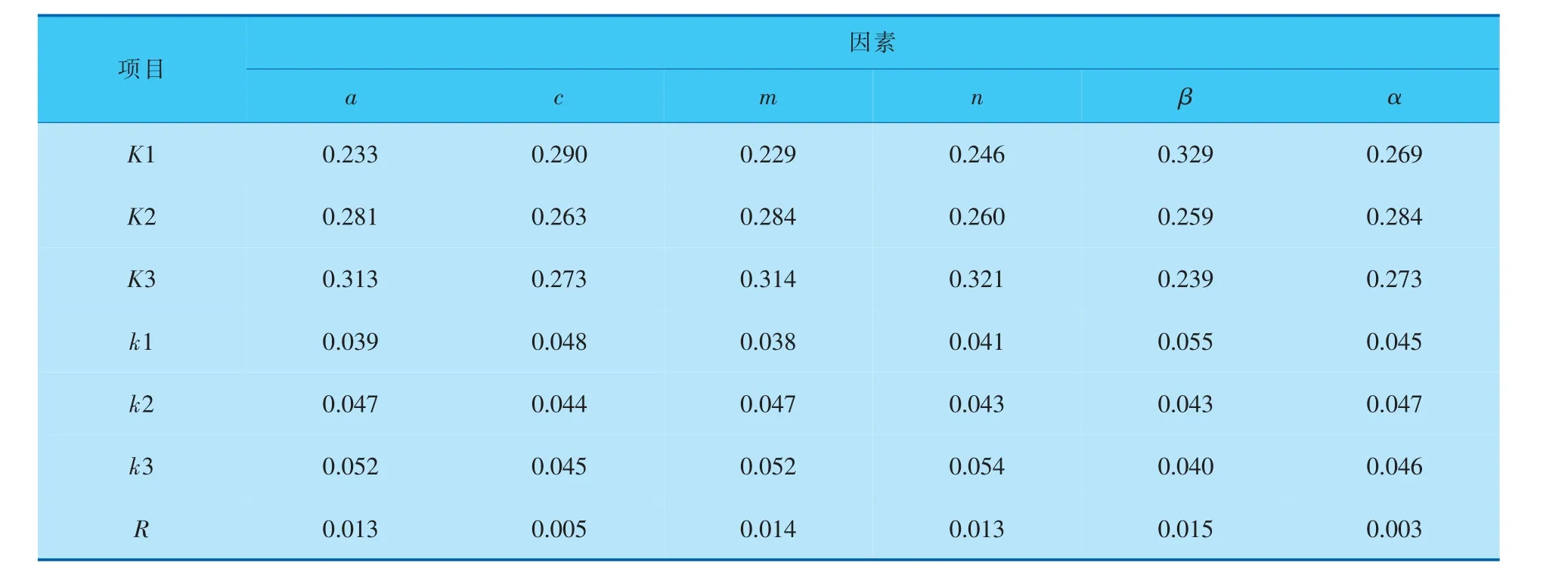
表3 f极差分析表
因素水平对PEC的影响见表4,各因素水平对PEC影响的主次顺序为: 扰流柱的相邻环圆周差角β>环向个数m>短轴长度a>扭转角α>长短轴之比c>轴向环数n。 图4中,扰流柱的相邻环圆周差角β的增大会大幅降低流动阻力而使PEC显著提高。 环形流道内的换热面积随着短轴长度的增加而增大,同时流场的压降也会相应增大,使Nu、f和PEC同时显著提高。 扰流柱环向个数和轴向环数的增加,仅会使Nu小幅度提升,但会大幅增加f,使得PEC大幅下降。 当扰流柱的长短轴之比大于1, 即采用椭圆形扰流柱对环形流道进行传热强化时,流场中的Nu、f和PEC均优于圆形扰流柱。此时优化组合方案是A3B2C1D1E3F3,即短轴长度为6 mm、长短轴之比为2、环向个数为1、轴向环数为6、相邻环圆周差角为60°、扭转角为30°。经数值模拟验证其Nu为1 341.46,f为0.032,PEC为1.973。

表4 PEC极差分析表
3 场协同分析
场协同原理[19]认为,对流换热的性能不仅取决于流体的速度、 物性和流体与壁面的温差,还取决于流体的速度场和温度场之间的协同程度。在相同的速度和温度边界条件下,速度场与温度场之间的协同程度越好,换热强度就越高。
管内对流换热的温降主要发生在径向,其径向温度梯度远大于轴向温度梯度, 一般径向温度梯度比轴向温度梯度大2~3个数量级甚至更多[20]。对于套管的环形流道内的温度场也具有相同规律。 因此,只要提高流体径向速度,即可对换热产生显著的影响。 图5是光管和PEC=1.973组合的套管环形流道内的径向速度和轴向速度绝对值之比沿径向方向的变化。 相较于光管,环形流道内设置的具有扭转角的椭圆形扰流柱使径向速度大幅提升,约可达到轴向流速的4%。

图5 径向速度和轴向速度绝对值之比沿径向方向的变化
取r/R=0.90处的柱面温度云图并沿圆柱母线展开,如图6所示。 可以看到具有扰流结构的环形流道内的温度场分布更均匀。 这种强化措施显著改善了流道内的场协同效果,起到了强化传热的作用。
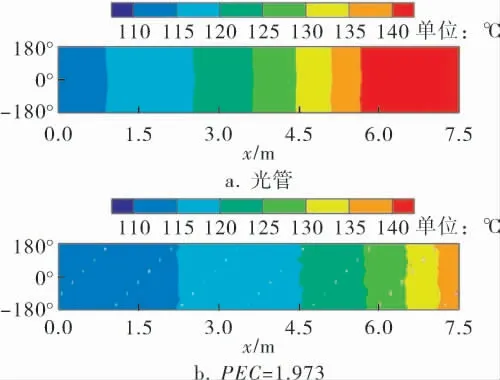
图6 r/R=0.90处的温度场圆周展开示意图
4 结论
4.1 基于数值模拟和正交试验结果对综合评价指标PEC进行极差分析, 套管中安装具有扭转角的椭圆形扰流柱的结构参数中,扰流柱的相邻环圆周差角对其流动特性和传热性能综合影响最大,并得出一组综合换热效果最优的结构参数组合,其PEC=1.973。
4.2 基于场协同理论分析,环形流道内设置的具有扭转角的椭圆形扰流柱使径向速度大幅提升,约可达到轴向流速的4%。这种强化措施显著改善了流道内的场协同效果,起到了强化传热的作用。
