计及柔性直流的系统短路电流实用计算方法
2023-12-28陈启超王智冬蒋维勇
陈启超,李 晖,王智冬,张 怡,蒋维勇,王 菲
(1. 国网经济技术研究院有限公司,北京 102209;2. 国家电力调度控制中心,北京 100031)
相比于常规直流输电技术,柔性直流输电VSC-HVDC(voltage source converter based high voltage direct current transmission)技术具有控制灵活、有功和无功可独立调节、无换相失败问题、占地面积小等优势,更适用于深入负荷中心改善潮流分布、整体提高电网的供电能力[1-5]。但负荷中心系统强度高,网架密集,往往面临短路电流超标问题。而VSC-HVDC可实现故障穿越,为减少系统恢复时间,短路故障期间不闭锁,同时也会向短路点注入短路电流,导致短路电流水平接近或超过断路器的遮断极限,短路故障难以清除,给系统安全稳定运行带来严重威胁。随着VSC-HVDC容量的增加,其对交流系统短路电流的影响已不容忽略。
相关学者已经针对VSC-HVDC对交流短路电流的影响与抑制开展了广泛研究。文献[5]基于换流站输出短路电流在基准相位下的相角值,提出了电流限幅与有功优先相结合的并网点短路电流降低策略;文献[6-7]分析了VSC-HVDC贡献短路电流的特性和机理,得出了限幅器幅值直接影响短路电流稳态值水平的结论;文献[8]分析了VSC-HVDC运行工况对短路电路的影响,提出了限制外环功率控制器的正序电流q轴指令值以降低贡献短路电流的方法;文献[9]分析了VSC-HVDC 贡献短路电流的暂态特性及关键影响因素,并指出提高计算精度的关键是正确处理短路电流间的相位差;文献[10]基于变流型电源的故障特性形成相应的阻抗矩阵,对高密度变流型电源并网的输电系统三相短路电流进行了准确评估;文献[11]给出了将VSC-HVDC等效为电流源参与交流系统三相短路电流计算的理论分析方法;文献[12-13]提出了提升多馈入短路比的VSC-HVDC控制策略,增强了对受端电网的稳定支撑能力。
已有研究对于含柔性直流接入的交流系统任意节点故障的短路电流计算较少涉及,无法支撑柔性直流工程在规划与设计阶段的短路水平校核。目前对含柔性直流接入的交流系统短路电流计算的研究主要有3 方面不足:①VSC-HVDC 输出电流限幅并与交流短路电流做简单叠加,高估了VSCHVDC 提供的短路电流,导致冗余的短路电流抑制措施;②简化柔直提供短路电流与交流短路电流的相位关系,做简单的矢量叠加,未考虑VSC-HVDC控制策略与控制参数、系统网架结构、运行方式等对计算结果的影响,往往存在较大误差;③通过电磁暂态仿真计算短路电流,由于构建模型复杂、仿真时间过长而缺少工程应用价值。此外,由于VSC-HVDC输出电流与并网点电压存在耦合关系,导致传统短路电流计算方法求解包含柔性直流的短路电流难以实现。为此,文献[14-15]提出了网络电压和故障网络短路电流相互修正的迭代计算方法,以及基于近似求解并网点电压解耦的等效网络短路电流统一求解方法,但也存在迭代计算不收敛及求解过程复杂等问题。
综上所述,本文首先根据电力系统运行方式确定系统的节点阻抗矩阵;然后,在分析VSC-HVDC控制策略及其输出电流特性的基础上,将其合理等效为幅值恒定的理想电流源,弱化了VSC-HVDC输出电流与并网点电压的耦合关系,进而提出一种基于叠加原理的计及VSC-HVDC 的三相交流短路电流计算方法;最后,通过PSCAD/EMTDC 搭建测试系统,验证了所提短路电流计算方法的有效性。
1 柔性直流输电控制策略
1.1 dq 解耦控制
对于并网运行的VSC-HVDC换流器,主要采取dq坐标系下的双闭环解耦控制,由内环控制器、外环控制器和锁相环PLL(phase locked loop)等构成,整体控制结构如图1所示。图1中,Vdc、Vrms分别为柔直直流电压值与并网点电压有效值,vd和vq、id和iq分别为柔直并网点电压vabc、输出电流iabc的d、q轴分量。内环控制属于直接电流控制,能够获得优良的动态响应性能,ud、uq为解耦控制生成的目标值,再经dq反变换后得到调制信号Uabc。外环控制根据控制目标,d轴可设置为参考值等于Pref的定有功功率控制或参考值等于Vdcref的定直流电压控制;q轴可设置为参考值等于Qref的定无功功率控制或参考值等于Vacref的定交流电压控制。d、q轴的PI 控制均设置限幅,同时为避免发生过流设置了限流环节,其中Id,max为d轴PI 控制输出的限幅,Iq,max为q轴PI 控制输出的限幅,Imax为限流环节输出的限幅,为限幅后注入内环控制的参考值。
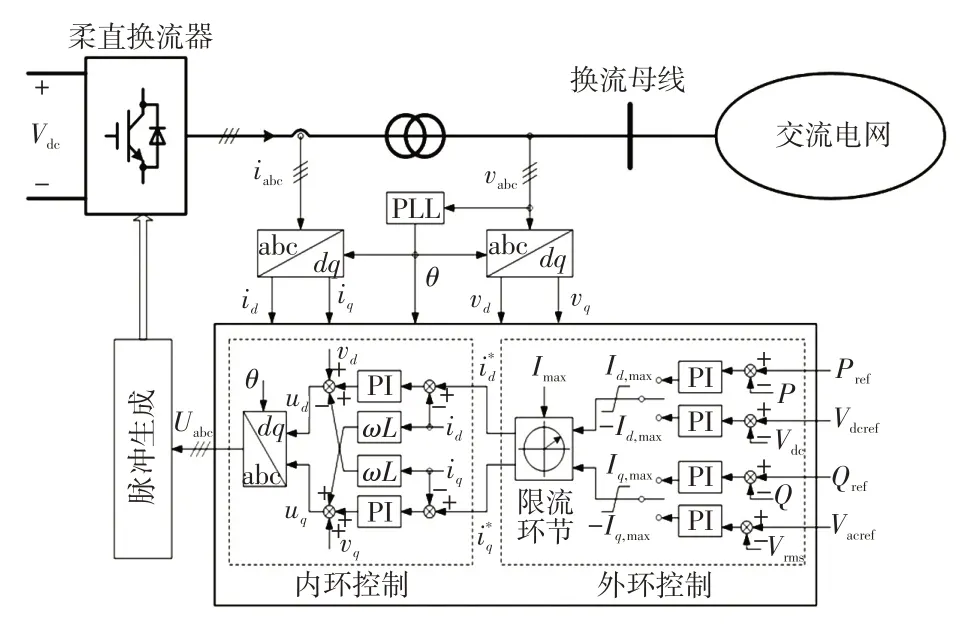
图1 柔性直流输电系统控制示意Fig.1 Schematic of control of VSC-HVDC system
1.2 低电压穿越控制
交流短路故障后,VSC-HVDC 并网点电压跌落,但因其具备低电压穿越能力仍然能够稳定运行。受限于换流阀开关器件的耐流能力,外环控制都设置了限流以防止过载。常用的限流方式主要有等比例、无功优先、有功优先[9],外环PI 控制的输出电流I经过等比例、无功优先、有功优先限流后得到的电流参考值分别为。不同限流方式下柔直内环参考值设定如图2 所示。相应的内环电流参考值具体设置如下。
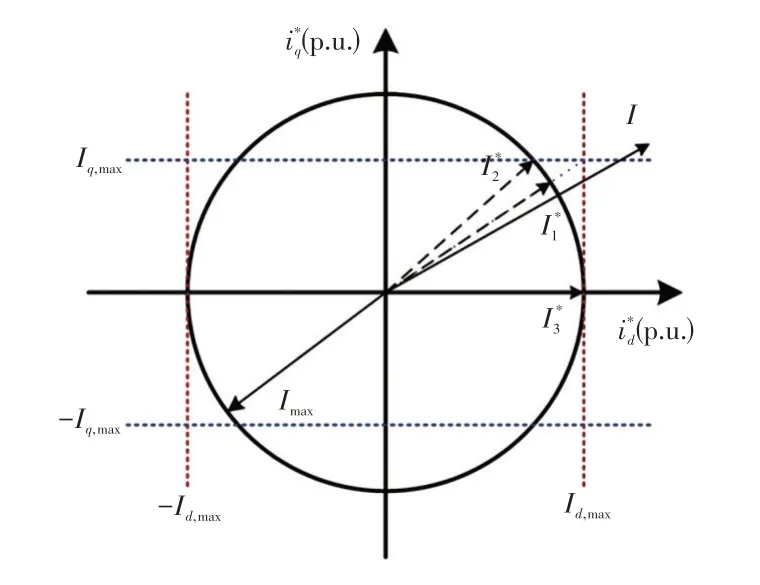
图2 不同限流方式下柔直内环参考值设定Fig.2 Reference value setting of inner ring-loop in different current limiting modes
(1)等比例限幅可表示为
(2)无功优先限幅可表示为
(3)有功优先限幅可表示为
低电压穿越控制中限流方式的差异将直接影响故障期间VSC-HVDC 输出电流与并网点电压的相角,进而影响VSC-HVDC提供的短路电流。
2 基于叠加原理的柔性直流输电提供短路电流计算方法
2.1 基于叠加原理的短路电流计算
电力系统三相短路计算主要是短路电流周期分量的计算,在给定电源电势时,实际就是稳态交流电路的求解,可利用节点方程进行故障计算[16]。首先根据给定的电力系统运行方式制定系统等值电路,形成不含发电机的节点阻抗矩阵Z。其中,负荷一般作为节点的接地支路并用恒定阻抗表示,在不要求精确计算的场合,可以不考虑负荷电流的影响。图3 给出了含VSC-HVDC 接入的多电源交流网络短路故障后系统的等值电路。系统中有n个节点接入发电机,每个发电机都等效为电压源与阻抗zi的串联支路(i= 1,2,…,n),VSC-HVDC 作为电压源型变换器也等效为电压源与阻抗zm的串联支路接入节点m,其输出电流与并网点电压分别为、。假设节点f发生短路故障,短路电流为。
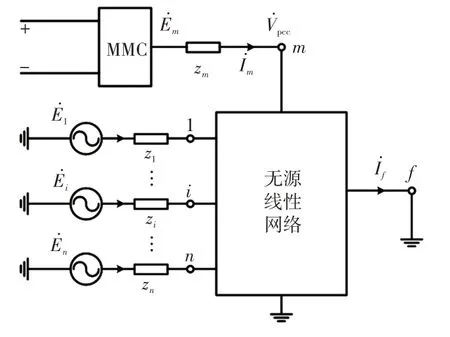
图3 含VSC-HVDC 接入的多电源交流网络短路故障示意Fig.3 Schematic of short-circuit fault of multi-power AC network connected with VSC-HVDC
当电网中只有电源i单独存在且其他电源都为0 时,系统等值电路如图4 所示,电源i提供的短路电流为
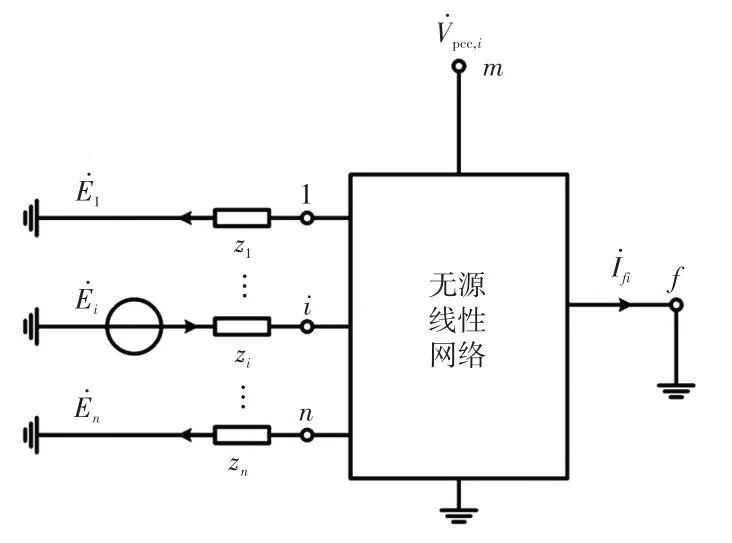
图4 单独电源提供短路电流示意Fig.4 Schematic of short-circuit current provided by single power source
式中,zfi为电源i对短路点f的转移阻抗,可表示为
式中:Zff为节点f的自阻抗;Zfi为节点f与节点i的互阻抗,可利用节点阻抗矩阵Z求得。
不含VSC-HVDC且电网中电源全部投入时,系统等值电路如图5 所示。根据叠加原理可以得出节点f的短路电流为
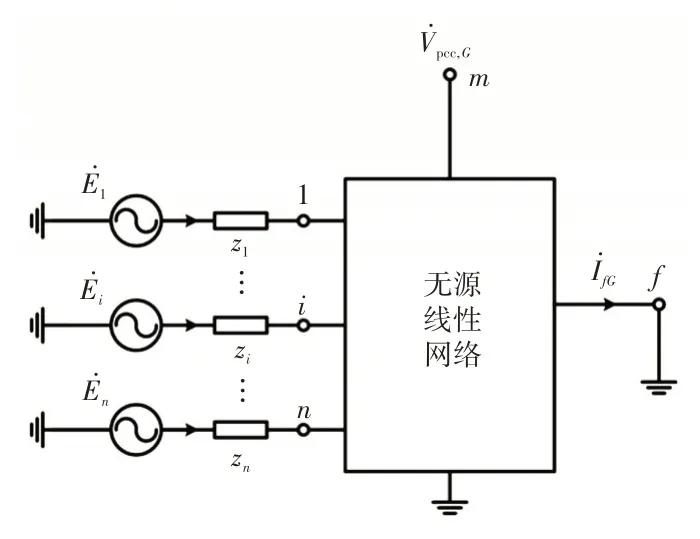
图5 不含VSC-HVDC 的多电源提供短路电流示意Fig.5 Schematic of short-circuit current provided by multiple power sources without VSC-HVDC
式中:Vpcc,G、α分别为并网点电压的幅值和相角;IfG、β分别为短路电流的幅值和相角。
2.2 VSC-HVDC 的等效算法
根据上述对VSC-HVDC控制策略的分析可知,正常运行时,外环控制作用下柔性直流呈功率源特性;故障穿越时,限流环节作用下柔性直流呈电流源特性,当进行计及柔性直流的短路电流计算时,可将其等效为电流源处理。但如果柔性直流采用基于PLL的跟网型控制策略,其特性应等效为压控电流源,即输出电流与并网点电压是耦合的。采用基于叠加原理的短路电流计算方法时,需进一步分析处理。
短路故障期间,VSC-HVDC进入低电压穿越控制。当短路点f发生在距离VSC-HVDC并网点m较近时,并网点电压跌落较深,VSC-HVDC 输出电流幅值达到限值Imax;当短路点f发生在距离VSCHVDC 并网点m较远时,并网点电压跌落不多,或是故障前VSC-HVDC输出电流较小时,故障期间输出电流幅值未达到限值Imax,但此情况下VSCHVDC 提供的短路电流本身有限,可假定VSCHVDC 输出电流达到限值Imax,虽然高估了VSCHVDC 提供的短路电流,但高估程度较小。同时,故障期间VSC-HVDC 输出电流与VSC-HVDC 低电压控制策略、故障前控制模式、控制参数设置等紧密相关,难以穷举计算。因此,计算短路电流时,可将VSC-HVDC 输出电流幅值设定为限值Imax,得到的结果是保守且合理的。

图6 VSC-HVDC 提供短路电流示意Fig.6 Schematic of short-circuit current provided by VSC-HVDC
式中,Zfm为柔直并网点m与短路点f的互阻抗,可利用节点阻抗矩阵Z求得。因此,可以得到VSCHVDC 等效电流源作用下并网点电压和短路电流的时域表达式分别为
式中:Vpcc,m、φ分别为电压的幅值和相角;Ifm、γ分别为电流的幅值和相角。
保持网络结构不变,当λ为任意值时,等效电流源与其生成的并网点电压之间的夹角θ1不变,其提供的短路电流与其自身的夹角θ2不变,生成的并网点电压与提供的短路电流的幅值Vpcc,m、Ifm也都不变,如图7所示。随着λ的变化,φ、γ也发生变化,体现在图7中只是波形平移。
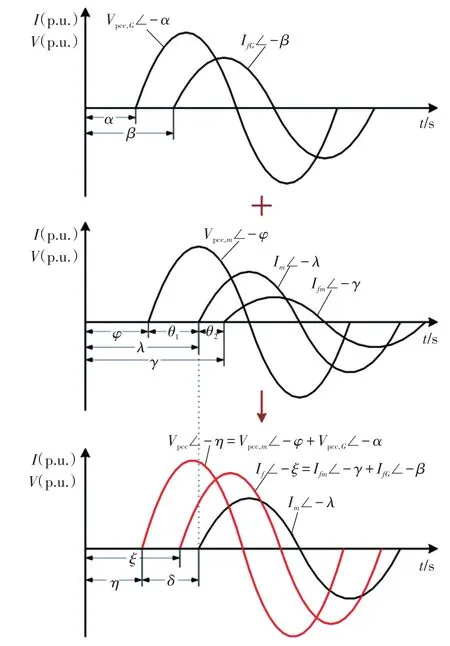
图7 VSC-HVDC 提供短路电流的计算原理Fig.7 Calculation principle for short-circuit current provided by VSC-HVDC
式中:Vpcc、η分别为电压的幅值和相角;If、ξ分别为电流的幅值和相角。
式(13)和式(14)的矢量相加体现在时域中的结果如图7 所示。而实际中,VSC-HVDC 采用的是跟网型控制,即通过PLL锁定并网点电压。故障期间经过限流环节后,可以确定VSC-HVDC输出电流与并网点电压的夹角δ。根据故障穿越策略及限流环节的设置可确定δ,限流环节可采取等比例、有功优先、无功优先等,以限流环节采取等比例限幅为例,角度δ可表示为
角度δ确定后,可以得到与的夹角为δ-θ1,则有
将式(18)代入式(15)可得
在复数形式下,根据实部虚部相等可得
由式(20)可以求解得
根据图7可得
由式(22)可求得γ,将γ代入式(14)进而可以求得f点短路电流为
2.3 计及VSC-HVDC 的短路电流计算方法
综合上述分析,本文提出了一种含VSC-HVDC接入的交流系统短路电流计算方法,具体流程如图8 所示。当系统中存在多回VSC-HVDC 接入时,可列写每个VSC-HVDC并网点电压的矢量叠加方程,然后统一求解。本文所提方法能够在考虑运行方式的情况下计算交流系统任意节点短路电流,同时还可以根据式(24)计算出VSC-HVDC 对故障点提供最大短路电流时输出电流的相角δIf,max,然后将δIf,max代入式(21)~(23)即可计算出考虑VSC-HVDC影响的故障点最大短路电流,为短路电流校核提供准确的计算结果,支撑相关的规划设计方案。同时,也可以计算VSC-HVDC提供最小电流时输出电流的相角δIf,min,进而可以制定相应的限流策略,以达到短路电流抑制效果。
3 仿真分析
为了验证所提短路电流计算方法的有效性,在PSCAD 仿真平台中搭建测试系统。仿真模型基于IEEE39 节点系统搭建,在不改变潮流的情况下将节点39 的电源替换为输出功率相同的VSC-HVDC系统,具体网络结构如图9 所示,其中VSC-HVDC的换流器采用模块化多电平结构,换流站主要参数见表1。
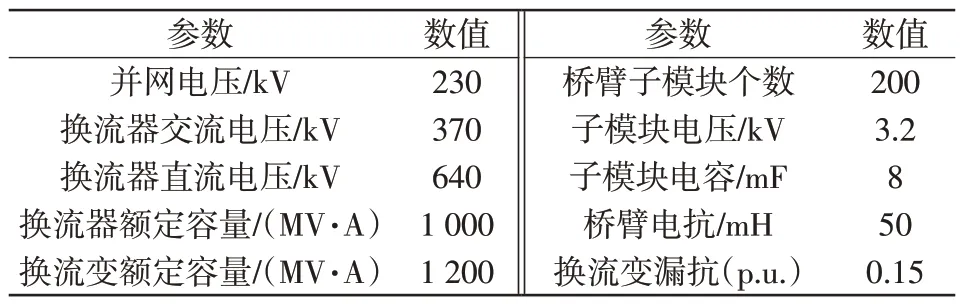
表1 VSC-HVDC 换流站主要参数Tab.1 Main parameters of VSC-HVDC converter station
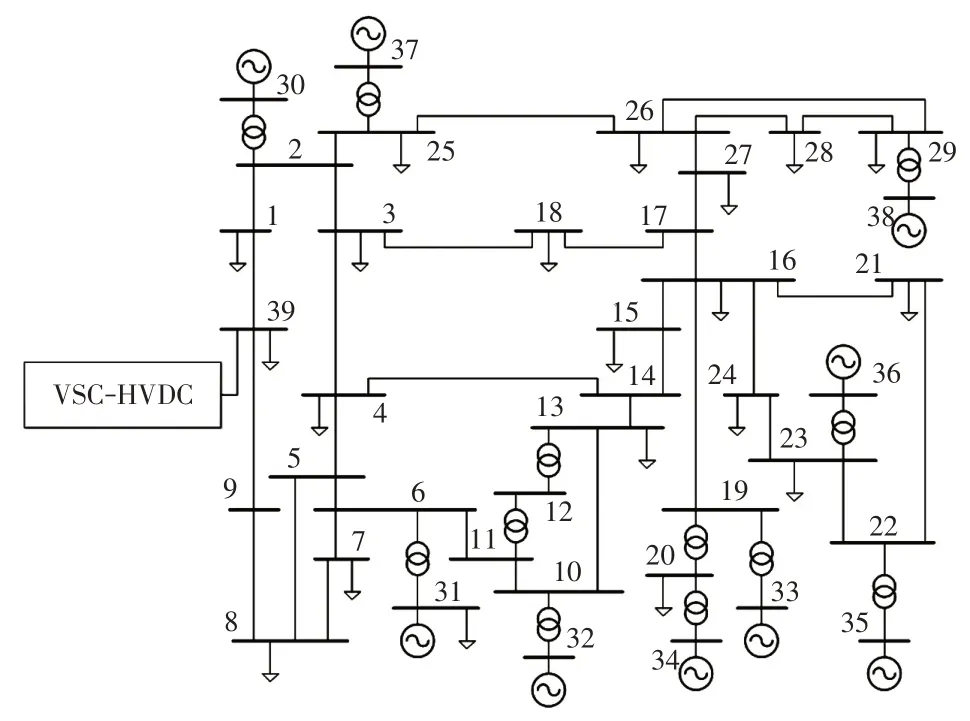
图9 含VSC-HVDC 的IEEE39 节点测试系统Fig.9 IEEE39-bus test system including VSC-HVDC
3.1 VSC-HVDC 等效电流源的仿真验证
在VSC-HVDC 并网点较远处节点16 设置三相金属性接地短路故障,在VSC-HVDC采用等比例限幅的详细控制模型下,分别针对故障穿越与闭锁、等效电流源3种情况进行仿真,计算故障点短路电流。VSC-HVDC详细控制模型的d、q轴分别采取定有功功率和定交流电压控制,限流环节设定为Id,max= 1.0 p.u.、Iq,max= 0.5 p.u.、Imax= 1.0 p.u.。根据式(17)可以得到VSC-HVDC 等效电流源输出电流与并网点电压的夹角δ= 26.6°。VSC-HVDC按照额定运行,具体仿真结果如图10所示。
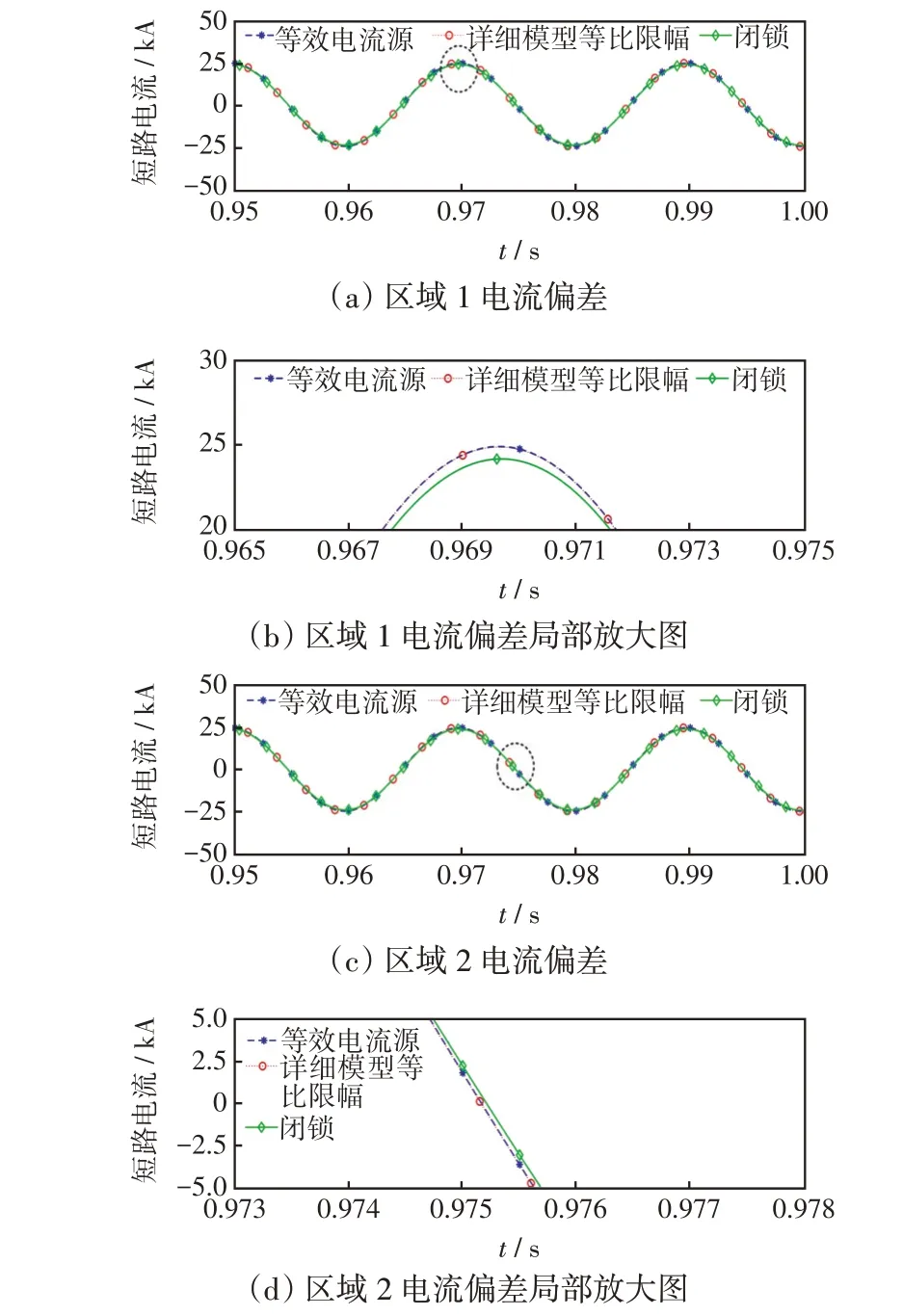
图10 3 种情况下短路电流的仿真结果对比Fig.10 Comparison among simulation results of shortcircuit current in three cases
从图10可以看出,VSC-HVDC闭锁后不向短路点注入电流。而在VSC-HVDC 不闭锁实现故障穿越情况下,短路故障发生后,VSC-HVDC 并网点电压跌落,VSC-HVDC 输出的无功功率增加,但并不能将并网点电压抬至额定状态,因此外环控制d、q轴的PI 输出均达到限值,经等比例限幅后,输入给内环的参考值分别为。仿真结果表明,VSC-HVDC贡献了约1 kA的短路电流,采用等效电流源与详细控制模型故障穿越的仿真结果保持一致。
针对不考虑VSC-HVDC 和采用等效电流源分别进行仿真,可得到参数α、β、θ1、θ2、Vpcc,m及Vpcc,G。由式(24)可计算出最大短路电流的相角δ=35.1°,此时短路电流应与不考虑VSC-HVDC时的短路电流同相位。保持Id,max= 1.0 p.u. 、Imax= 1.0 p.u.不变,根据式(17)可以求得Iq,max= 0.7 p.u. ,故障期间经等比限幅后有。仿真结果表明,修改q轴限幅后,VSC-HVDC采用等效电流源与详细控制模型故障穿越下的短路电流仍然保持一致,且与详细控制模型闭锁下的短路电流同相位,VSC-HVDC 贡献的短路电流增加了约0.05 kA。
改变详细控制模型的限幅及相应地设置等效电流源相角进行仿真,两种情况下节点16 的短路电流都能保持一致且小于相角δ= 35.1°。仿真结果验证了上述VSC-HVDC 提供最大短路电流分析的正确性与等效电流源的有效性,如图11所示。

图11 VSC-HVDC 提供最大短路电流仿真结果Fig.11 Simulation results of maximum short-circuit current provided by VSC-HVDC
3.2 所提理论计算方法的仿真验证
采用所提方法分别对节点8、节点18、节点26开展计及VSC-HVDC情况下的短路电流计算,并与仿真结果进行对比。其中,仿真采用等比例限幅的详细控制模型,有功环为定有功功率控制,无功环为定交流电压控制,限流设置为Id,max= 1.0 p.u. 、Iq,max= 0.5 p.u.、Imax= 1.0 p.u.。仿真值与理论计算值对比结果如表2所示。对结果对比分析可知,所提短路电流计算方法能够准确有效地计算出计及VSC-HVDC的交流短路电流。
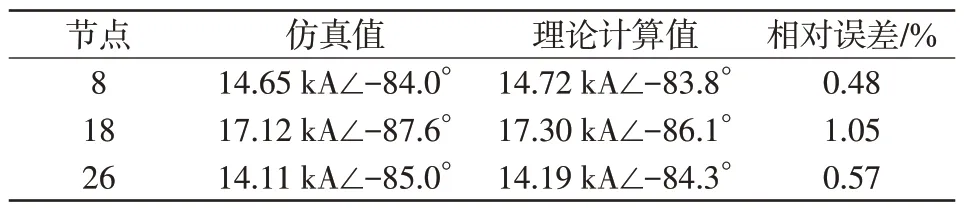
表2 不同节点短路电流的仿真值与理论计算值对比Tab.2 Comparison between simulation and theoretical calculation values of short-circuit current at different nodes
由于VSC-HVDC控制响应迅速,故障过程中输出电流可认为不存在直流分量与非周期分量[6],并可以不考虑二者影响。因此,在计算起始次暂态电流时,仍可以采用本文所提方法,只需将系统元件都用次暂态参数表示即可。
4 结 论
针对具有VSC-HVDC 接入的交流系统的短路电流计算难以求解的问题,本文在分析交流系统发生短路故障后VSC-HVDC 注入系统电流特性的基础上,将VSC-HVDC 等效为合理简化的理想电流源,提出了基于叠加原理的计及VSC-HVDC的短路电流计算方法。主要结论如下。
(1)VSC-HVDC在短路故障期间进入低电压穿越控制,分析其对短路电流的影响,将其等效为幅值固定且等于所设定限值的电流源,弱化VSCHVDC 输出电流与并网点电压的耦合关系,计算出的短路电流结果是保守且合理的。
(2)将VSC-HVDC 等效为电流源后,短路电流计算转化为不同电源提供短路电流的矢量叠加,VSC-HVDC 提供的短路电流可通过其输出电流与并网点电压的夹角来求解。
(3)所提方法可对含有VSC-HVDC接入的交流系统三相短路电流进行准确评估,为电网规划设计和运行方式制定提供依据。
