一种基于双层纳什博弈的微电网双层电能交易策略

2023-12-28朱瑞金崔世庭

电力系统及其自动化学报 2023年12期

朱瑞金，吴军，崔世庭

（1. 西藏农牧学院西藏土木水利电力工程技术研究中心，林芝 860000； 2. 西藏农牧学院电气工程学院，林芝 860000； 3. 武汉大学电气与自动化学院，武汉 430072；4. 西藏农牧学院水利土木工程学院，林芝 860000）

微电网MG（microgrid）作为一种微型电力系统，已广泛应用于电力系统中[1]。然而单个MG的调控能力不足，并且受到运行环境变化的影响，其抗干扰能力有限[2]。

随着MG 技术的发展，多个MG 可以通过一个公共耦合点连接起来，以构建微电网群MGC（microgrid cluster），使MG 可以与上级电网或其他MG相互协作，以获得稳定的电力支持[3]，并有效提升本地可再生能源RE（renewable energy）的消纳能力，减少对上级电网的依赖[4-5]。目前，MGC已被用于许多实际工程中[6]。但是，不同MG在结构、供需水平、合作需求等方面存在差异，同时MG之间的电能、信息和资金的多方向流动及MG之间的互动协调与电能共享也会使MGC 的组成和拓扑结构更复杂、规模更大，更难协调和控制[7]。

目前，MGC的电能交易方式可划分为集中式和分布式[8-9]。集中式交易存在通信信息量大、涉及各主体隐私等缺点；分布式交易种类较少，难以解决分层、多主体交易中MG 的全局优化问题。相比之下，端对端P2P（peer-to-peer）交易方式可通过有限的信息交互实现MG 之间的电能交易，既可保护用户隐私，又具有去中心化、易于扩展的优势[10-11]，因此在MGC 电能共享和电能交易中得到广泛的应用[12-13]。随着MG 的增多，在多数应用场景中（例如偏远地区、海岛等），常形成“一配网多微电网群互联”的树形结构，即配网的每个支路都与多个MG互联，使单个MGC难以适应调控需求。

目前，针对MGC电能交易的研究主要有3个方面：①借助区块链技术实现产消者P2P电能交易[14]，但目前未得到大规模应用；②基于联邦学习进行隐私计算[15]，但存在数据训练量大和算力成本高的问题；③利用博弈论来解决P2P交易[16]，该方法应用最为广泛，包括非合作性博弈和合作性博弈[17]两种。非合作博弈模型的各主体只追求自身的利益最大化，忽视了主体间的协调互动，因此很难考虑整体能源效率[18-20]。而合作博弈通常基于联盟博弈或纳什博弈，故联盟博弈模型只能实现部分全局最优[21]。基于纳什博弈模型可以保证所有参与者的利益，并克服上述问题[22]。文献[9]建立了基于纳什博弈理论的激励机制，提升了MG 个体参与交易电能的积极性，并通过交替方向乘子法ADMM（alternating direction method of multipliers）进行分布式求解，有效保护MG 个体的隐私。文献[23]建立了MGC的合作博弈模型，利用纳什议价来协调微电网之间的收益分配，并分析MG 之间的最优交易功率和电价。文献[15]研究表明联邦学习效果要优于非合作博弈、机器学习的方案，但并未对比合作博弈。文献[24]基于联邦学习对机器学习算法进行训练，用于管理多MG 协同运行。现有研究主要集中在单个MGC 的电能交易，无法适应配电网-MGCMG之间互动交易的需求。文献[25-26]也指出不考虑MG 对电能共享的不同贡献，有利于提升利润分配的公平性。因此，有必要在构建MGC间和MG间的双层电能交易的同时，考虑更加公平的利润分配模式。

综上所述，本文提出一种基于双层纳什博弈的微电网双层电能交易策略。首先，依据配电网支路构建MGC，形成MGC-MG 的双层结构，并构建双层电能交易模型，各主体仅通过有限信息进行交易，在确保优化效率的同时满足主体隐私需求。然后，借助纳什博弈理论和ADMM，构建社会成本最小化和利润分配两个子问题。社会成本最小化问题通过双层电能交易模型求解。在MGC 优化中，尝试借助改进多变异协作差分进化IMMCDE（improved multi mutation cooperative differential evolution）算法和Gurobi 求解器共同辅助ADMM 求解。对于利润分配子问题，以公平利润分配为目标，构建MGC议价模型，并借助电能共享贡献指数改进MG 利润分配模型，以实现多主体利益公平分配，提升MG在电能交易中的经济性。最后，设置场景验证所提模型的有效性和利润分配的公平性。

1 微电网群电能交易模型

图1为交易模型结构。图1中，模型包含i={1,2,…,N} 个MG，并依据支路位置组成j={1 ,2,…,M}个MGC，MGC 由微电网聚合商MGA（microgrid aggregator）管理。交易模型分为双层，并通过对应的母线公共节点进行电能交易，上层交易发生在MGC之间，下层交易发生在MG 之间，MGC 作为中间载体实现不同区域MG 的交易。与单层交易相比，双层交易模型可以减少通信压力和远距离电能输送量。

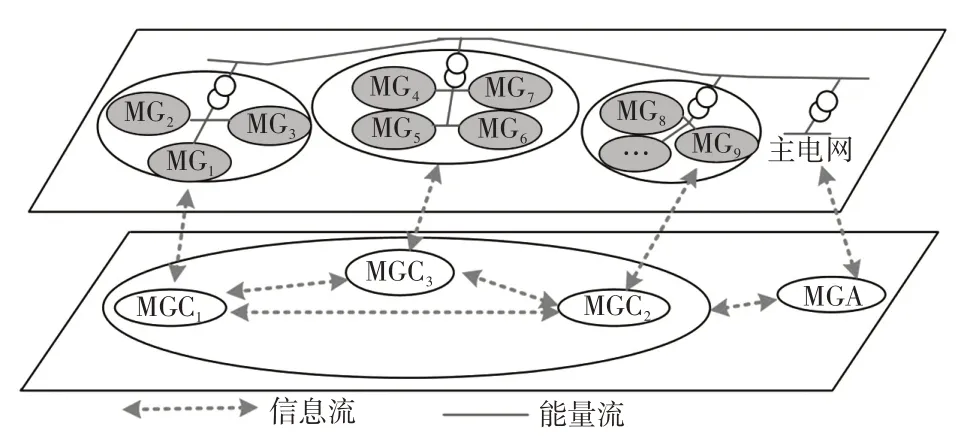
图1 交易模型结构Fig.1 Structure of trading model

MG的运营目标为消纳RE、满足供需平衡和实现效益最大化等；MGC的运营目标为实现MG间互联互济和上层交互电能成本最小化；MGA的运营目标为协调各主体参与电能交易，实现效益最大化。MGA、MGC和MG之间通过无线通讯的方式进行信息交互，例如4G/5G。考虑到隐私保护的问题，MG和MGC 只交互期望功率信息，内部优化策略在本地求解。在电能交易中，优先考虑与同一MGC 内的MG进行交易，其次是其他MGC的MG，最后是上级电网，且遵循由近到远的交易原则。

1.1 MG 结构

MG 结构如图2 所示。MG 配备有燃气轮机GT（gas turbine）、有机朗肯循环ORC（organic Rankine cycle）、RE 发电装置和电储能，其中ORC 用于余热发电，能量管理系统负责信息交互、优化设备单元的出力及负荷的需求响应DR（demand response）计划。

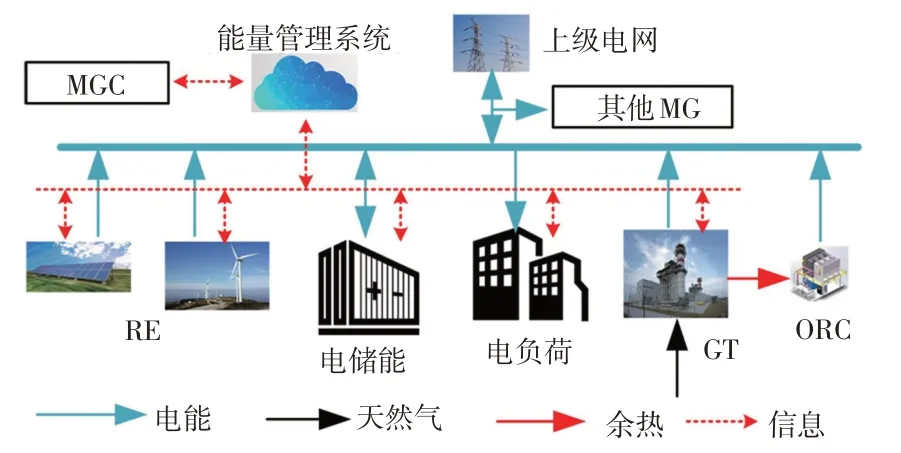
图2 MG 结构Fig.2 Microgrid structure

各MG 可以与配电网进行电能交互，应满足如下约束：

式中：Pbuy,i,t、Psell,i,t分别为向配电网的购电量和售电量；Pbuy,i,t_max、Psell,i,t_max分别为购电、售电量的上限。

MG的RE消纳模型可表示为

式中：Pre,i,t为MG 的RE 发电功率；Pre,cur,i,t为MG 的RE损耗功率；Pre,pre,i,t为MG的RE预测发电功率。

每个MG 以自身运行成本最小为目标，包括燃气成本Cfuel,i,t、DR 成本Cdr,i,t、向电网购售电成本Cgrid,i,t、储能运行维护成本Ces,i,t、RE 损耗成本Ccur,i,t。每个MG的目标函数及约束条件可表示为

式中：CMG,i为各MG 交易后的运行成本；Fgas,i,t为燃气量；cgas为天然气的价格；ctran、ccut为负荷的DR成本系数，kW/¥ ；μbuy、μsell为电网的购电价与售电价；ces为电储能系统的运行维护成本系数，kW/¥ ；ccur为RE 损耗成本系数，kW/¥ ；πi为MGi的电能交互成本；Pch,i,t、Pdis,i,t分别为储能系统的充电、放电功率；Pcut,i,t为电负荷削减量；Ptrani,t为电负荷转移量；T为运营优化周期。

GT 通过燃烧天然气产生电能，然后将余热传输至ORC进行发电，两者的出力可表示为

其中

式中：PGT,i,t为GT 的发电功率；PORC,i,t为ORC 的发电功率；PG+O,i,t为GT和ORC的总发电功率；ηGT为GT 的发电效率；HLHV为天然气低热值；ηORC为ORC的发电效率。

MG 内的DR 模型、燃气轮机和ORC 的约束、储能模型参考文献[27]进行建模，不再赘述。

功率平衡约束为

式中：Psha,i,t为MG 的期望共享功率，Psha,i,t＞0 表示MG 可共享多余的电能给其他MG；Le,i,t为DR 后的负荷。

共享功率约束为

式中：Psha,j为MG电能交易约束；Wsha,j,t为MGC期望共享功率；Wsha为MGC电能交易约束。

1.2 双层电能交易模型及其求解方法

MGA 收集内部Psha,i,t和Wsha,j,t，发布MGA 期望的MGC 共享功率Esha,j,t和MG 共享功率Qsha,i,t。MGC 收集Psha,i,t，并实现运营目标优化。MG 根据Qsha,i,t进行本地优化，并上报Psha,i,t。MGC 和MG作为独立主体，只代表自身利益。本文基于双层纳什博弈，建立双层电能交易模型，以最大化利润为目标。然后在MGC内部，依据MG各自的利益进行利润二次分配，以提升交易的公平性。本文模型可表示为

式中：Cgap,j为MGCj合作前后成本的差值；Cpre,j、Cpost,j分别为MGCj合作前、后的成本；τj为MGCj能量共享收益，τj> 0 表示MGCj共享多余的电能从其他MGC获得收益；M为参与能量共享的MGC的个数。

纳什谈判模型（见式（10））是一个非凸非线性优化问题，该模型同时优化两个变量，即交易电量和支付成本，直接求解难度较大，故将其转换为2个易于求解的子问题，即社会成本最小化子问题和支付谈判子问题。

1.2.1 社会成本最小化子问题的双层能量共享模型及优化流程

（1）MG 间能量共享问题的目标是社会成本最小，可以使用增广拉格朗日函数重新描述，即

式中：ρ为社会成本最小化子问题中MG 间的惩罚因子；αi为社会成本最小化子问题中MG间第i个拉格朗日乘子；λ为常系数；N为参与能量共享的MG的个数。

（2）MGC的目标函数及约束条件可表示为

（3）MGA 的目标函数可表示为

社会成本最小化子问题的优化流程如图3 所示，其中ξ为收敛精度，ξ= 0.01 ，k1和k2分别为内层和外层的迭代次数。

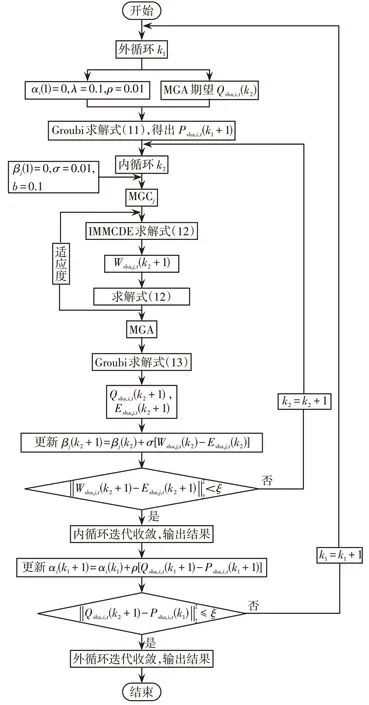
图3 社会成本最小化子问题优化流程Fig.3 Social cost minimization sub-problem optimization process

社会成本最小化子问题包括内、外两个循环，外循环负责下层优化，借助Gurobi 求解器求解MG最小社会化成本（见式（11））。Psha,i,t(k1+ 1) 和Qsha,i,t(k2)互为对偶变量，设Qsha,i,t(k2= 1) = 0 。内循环负责上层优化，本文借助IMMCDE算法和Gurobi求解器共同在内循环中辅助ADMM求解MGC最小社会化成本问题。

首先，利用IMMCDE 算法求解式（12），得出MGC 的Wsha,j,t和最小过网成本；其次，借助Gurobi求解器求解式（13），得出Esha,i,t和Qsha,i,t，并更新βj和进行MGC交易收敛性判别，若符合收敛精度，则完成内循环；最后，在外循环中更新αi和MG 交易收敛性判别，若符合收敛精度，则完成外循环。

1.2.2 IMMCDE 算法模型

综合考虑模型求解的需求，本文对标准差分进化DE（differential evolution）算法进行改进，避免局部最优并提高收敛速度。具体算法如下。

（1）改进交叉概率CR 和放缩系数F。引入加权Lehmer均值修正CR、F，即

式中：ACR 为CR 的加权Lehmer 均值修正值；CRk为第k代交叉概率且服从柯西分布，CRk=randc( C R,0.1) ；fbest,k为第k代全局最优参考值；fk为第k代适应度；wF为F的权重，而Fk= rand( )F,0.1为正态分布；MCR 为CR 的权重修正值；wCR,k为MCR 的权重；c为常数；K为最大迭代次数。F与CR 的修正策略类似，不再详细叙述。

（2）变异协作策略可分别表示为

式中：AF 为F的加权Lehmer 均值修正值；p、pbest和pbad分别为种群个体、最优个体和最差个体；pr1、pr2、pr3为种群的随机个体；Gbest为全局最优个体；N( ) 为高斯分布；δ为常数；；v1、v2和v3分别表示3 种变异策略。策略v1用于提升全局寻优能力，当pbest进入局部最优时，用Gbest引导pbest跳出局部最优。正常寻优时也会加速收敛。

（3）通过并行变异策略选择适应度f(v)。适应度f(v)可表示为

1.2.3 支付谈判子问题的议价和利润分配模型

在完成电能交易后，根据支付谈判子问题中MGC 的主体需求，求解最小化交易成本，并根据MG的主体需求，分配电能交易产生的利润。因此，本文采用议价谈判实现MGC 间电能交易成本最小化，通过利润分配向MGi分配收益。

1）MGC间的议价模型

式中，κj为MGCj合作后的交易成本，κj=Wsha,j,tηp,j,t。

依据ADMM原理建立MGCj的议价模型，即

式中：ηp,j,t和为MGC 间的共享电价，互为对偶变量；γj为MGCj的拉格朗日乘子；ς为MGC 间议价模型的惩罚因子。

2）MG不对称利润分配模型

MGC 完成议价支付后，MGC 内部的各MGi根据自身利益分配MGC的利润。考虑到MGi对电能共享的贡献不同，参考文献[25]引入MGi的电能共享贡献指数，以建立MG 利润分配问题的优化模型，即

式中：θ为MGi不对称利润分配模型的惩罚因子；τi为各MGi期望分配的利润；为MGA 期望MGi得到的利润；为各MG合作前后的成本差值。

其中

对于任意i，令和，并作为电能交易贡献的最大边界。由于为负值、为正值，始终小于0，始终大于0，故，同时w+≥w-，因此根据式（24）可得出。这样使得MG 有正向的议价能力，同时避免参数过大而影响收敛。

MGA的优化模型为

支付谈判子问题的求解流程分为MGC 间的议价支付和MG不对称利润分配两个阶段。具体流程不再论述。

2 算例分析

2.1 基础数据和情景设置

本文以图1中的MGC1和MGC2为例进行说明，MGC1接入风机WT（wind turbines），MGC2接入光伏PV（photovoltaic），各MG的电负荷如图4（a）所示，风光预测出力Pre,pre,i,t如图4（b）所示，系统运行参数见表1。

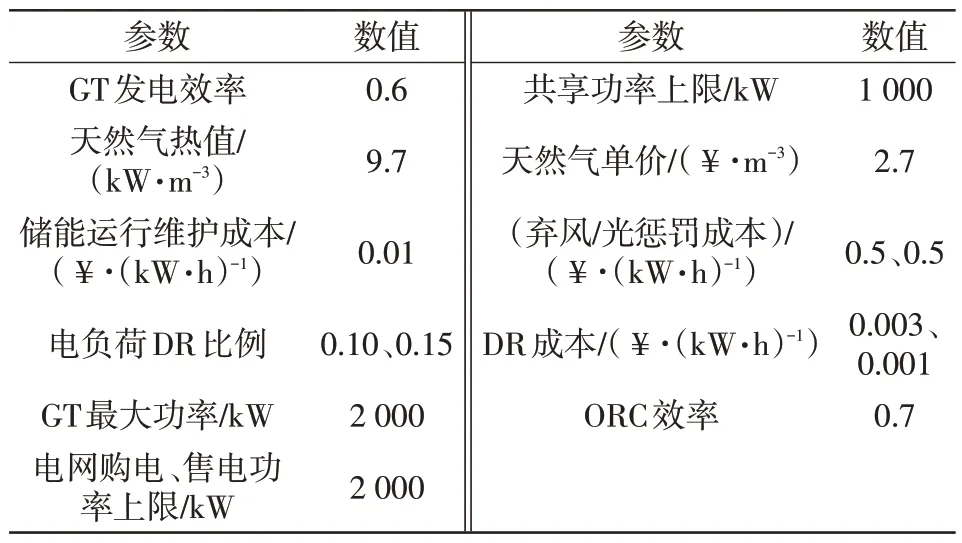
表1 MG 系统运行参数Tab.1 Operation parameters of MG system

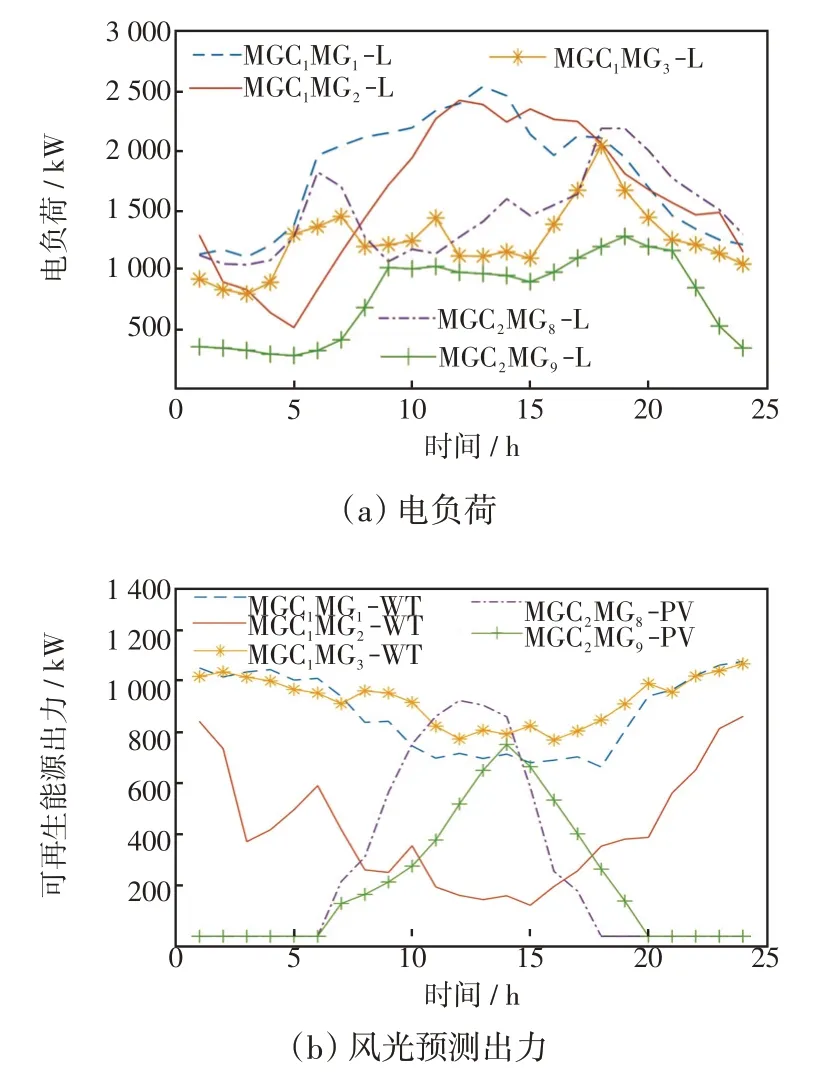
图4 电负荷和风光出力预测Fig.4 Forecasting of electrical load and WT/PV output

根据社会成本最小化子问题和支付谈判子问题的相关公式，可以通过设置以下5个场景求解不同的优化结果。

场景S1：基础场景，不考虑MG 合作，各MG 独立运行。

场景S2：不考虑MGC 电能交易，仅考虑MG 单层电能交易。

场景S3：采用本文所提的双层电能交易模型。

场景S4：借助MG纳什博弈进行对等利润分配。

场景S5：采用本文所提的MG不对称利润分配。

考虑风光出力占比为100%、80%和60%的情况，用于模拟Pre,pre,i,t受不同天气影响。此外，设置λ取不同值分别进行仿真，用于对比其对利润分配的影响。

2.2 优化结果分析

图5 中给出了MG1的功率平衡。可见，在WT出力不足时，GT 与ORC 补足功率缺额；在高电价时，储能放电并向电网售电，低电价时储能充电；DR 集中在负荷高峰和高电价时段。图6 为MG 交易电能曲线。结合图4，MG 的净负荷基本都为正值，这表明风、光的出力余量并不多。相较于同其他MGC进行共享电能，MG会优先与同一MGC内的MG 进行共享电能，以减少MG 的购电量，而额外的电能会通过MGC进行共享。

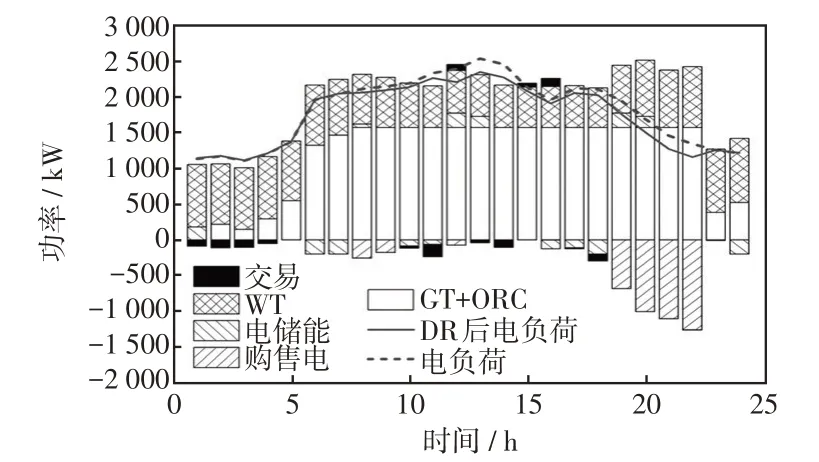
图5 MG1 机组和负荷功率平衡Fig.5 Power balance between MG1 unit and load

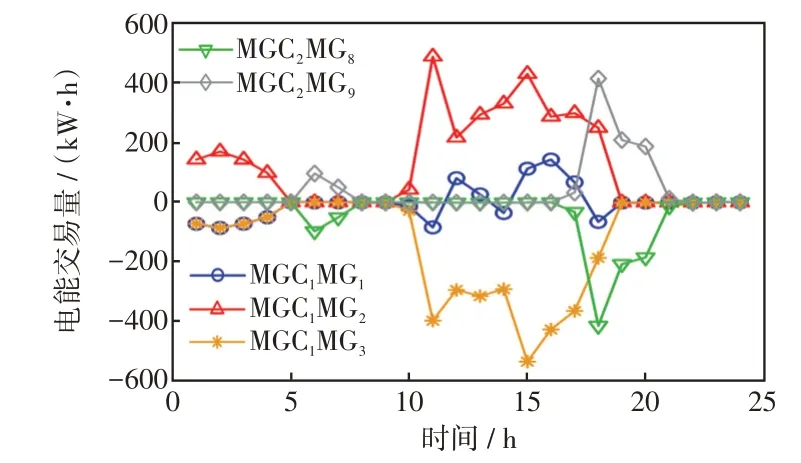
图6 MG 电能交易结果Fig.6 Power trading result of MGs

图7给出了MGC之间共享电功率的电价，可以看出，MGC 之间通过合作博弈，得到最优的共享电价，使各MGC 得到帕累托最优收益。详细的成本结果见表2和表3。

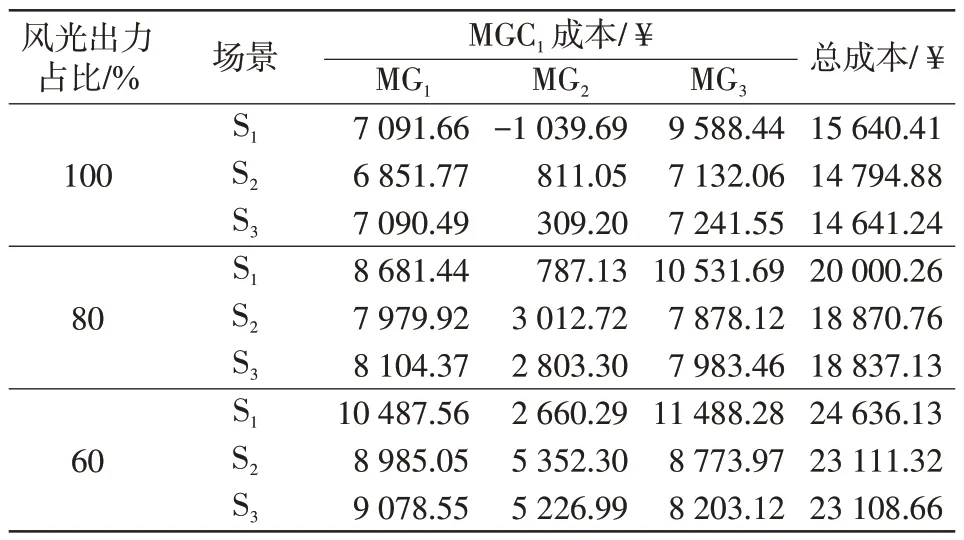
表2 不同情景的MGC1 优化结果Tab.2 MGC1 optimization results under different scenarios

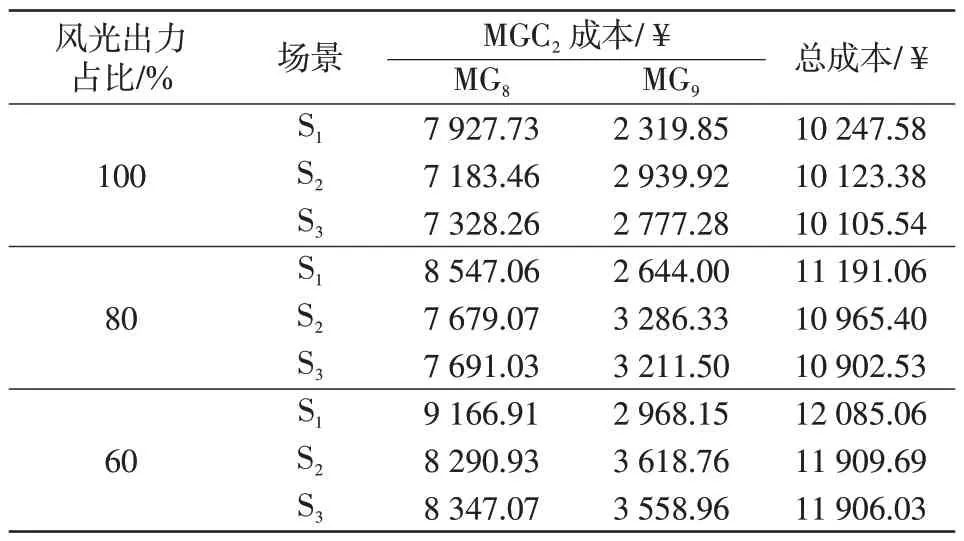
表3 不同情景的MGC2 优化结果Tab.3 MGC2 optimization results under different scenarios

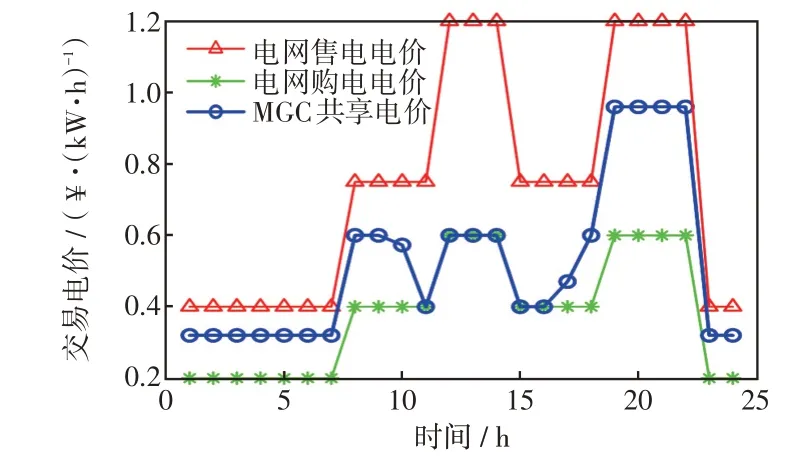
图7 电网电价与MGC 间交易电价Fig.7 Grid price and trading price between MGCs

表2 和表3 分别给出了MGC1和MGC2的优化结果。可见，随着风光出力降低，MGC在场景S1和场景S2下的总成本差值减少，这主要是由于MG的剩余能量减少，额外供应给MGC 间交易的电能减少。因此，风光出力越高，双层电能交易模型的效果越好，MGC间电能交易的作用越大。不同风光出力下，对比MGC在场景S1～场景S3下的总成本可以得出，配电网-MGC-MG 双层电能交易模型效果更好，能够为MGC带来更多的收益。

在表2 中，由于MG2把更多的电能用于和MG3交易，不同风光出力下，MGC1中MG2的成本都出现大幅度上升，MG1和MG3的成本都出现大幅度下降，这表明各MG 对于电能共享的贡献不同，其中MG2的贡献最大，MG3次之，MG1最小。

在表3 中，由于MG9把更多的电能用于和MG8交易，不同风光出力下，MGC2中MG9的成本都出现大幅度上升，MG8的成本都出现大幅度下降。这表明各MG 对于电能共享的贡献也不同，其中MG9的贡献最大，MG8最小。由表2和表3可知，在风光出力占比为100%时，相较于场景S1，本文所提模型（场景S3）成本下降了1.46%，相较于场景S2，本文所提模型（场景S3）成本下降了0.69%；在风光出力占比为80%和60%时，总成本同样低于场景S1和场景S2。这表明本文所提的双层纳什博弈模型经济效益更好。

表4给出了利润分配结果对比，其中场景S5和场景S4的总成本分别为1 141.29 ¥ 和1 141.21 ¥ ，支付谈判子问题中MGC1支付给MGC2的共享成本为119.33 ¥ ，过网成本为1.26 ¥ ，可忽略不计。不对称利润分配方案中，根据不同的，在优化结果中改变了各MG的利润分配值。相较于对等利润分配方案，降低了MGC1中MG1和MG3分配的利润，提升了MG2分配的利润。 MGC2与MGC1类似，这对MG更加公平。因此，相较于对等利润分配，不对称利润分配更加合理。

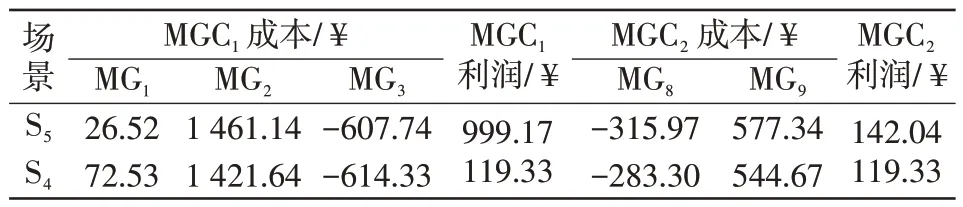
表4 不同场景的利润分配Tab.4 Profit allocation under different scenarios

表5 为不同参数的量化贡献，其中当λ= e 时，MG1、MG2、MG3、MG8、MG9的分别为0.29、1.72、0.63、0.63、1.74。

从表4 和表5 可以看出，MGCj利润固定，当λ从2变化到4时，随之增加，而且越大，MGi分配的利润越多。只有MGC1中MG2和MGC2中MG9分配的利润在提升，其他MG 分配的利润均在降低。结果表明，λ表示MG 参与电能交易时对电能贡献的重视程度，λ越大，越重视MG的贡献。

2.3 算法分析

图8 为社会成本最小化子问题优化迭代。可以看出，社会成本最小化子问题经过34 次迭代后收敛，本文所提模型只需要交互MG和MGC的期望功率，在有限信息下即可完成收敛，并达成电能交易共识，有效保护各主体隐私。支付谈判子问题与社会成本最小化子问题类似，不再论述其迭代过程。

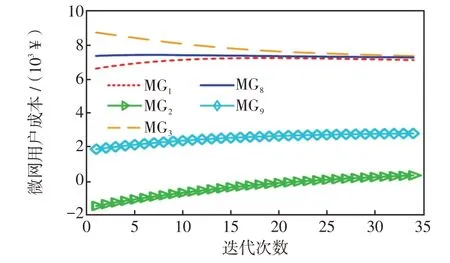
图8 社会成本最小化子问题优化迭代Fig.8 Social cost minimization sub-problem optimization iterations

表6 对比了3 种辅助ADMM 求解方式的成本，其中A1为Gurobi 求解器辅助ADMM 求解，A2为IMMCDE 算法和Gurobi 求解器共同辅助ADMM 求解，A3为DE算法和Gurobi求解器共同辅助ADMM求解。

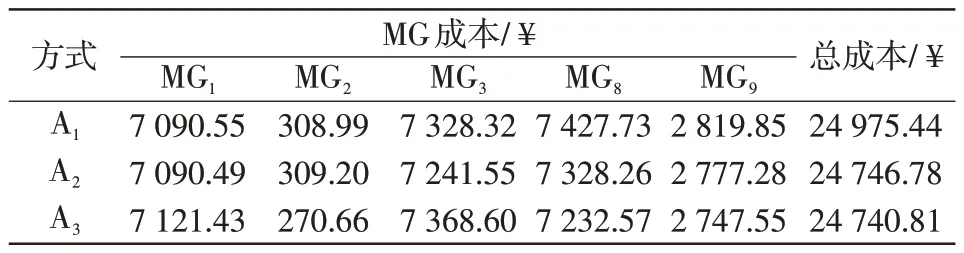
表6 不同求解方式下的MG 成本Tab.6 MG cost under different solution methods

从表6可以看出，当采用A1方式时，MG总成本为24 975.44 ¥ ，过网成本为87.16 ¥ ；当采用A2方式时，MG总成本为24 746.78 ¥ ，相比于A1方式，A2方式的MG 总成本下降了0.92%，同时A2方式也降低了MGC 间的电能交互量，过网成本大幅度下降至1.26 ¥；当采用A3方式时，MG总成本为24 740.81 ¥ ，过网成本为10.95 ¥ ，但不能达到收敛精度。