Thin-shell wormholes and modified Chaplygin gas with relativistic corrections

M Z Bhatti,Z Yousaf and M Yousaf

Department of Mathematics,University of the Punjab,Quaid-i-Azam Campus,Lahore-54590,Pakistan

Abstract In this paper,we analyze thin-shell wormholes from two identical copies of charged static cylindrically symmetric spacetimes using Visser’s ‘cut and paste’ approach under the influence of f(R,T) gravity Harko,Lobo,Nojiri,and Odintsov (2011,Phys.Rev.D 84,024020).In this scenario,the modified Chaplygin gas supports the exotic matter in the shell which allows,one to examine the dynamics of constructed wormholes.We utilize the junction condition to connect the interior and exterior geometries across the hypersurface and calculate different components of the Lanczos equation recently computed by Roza in Rosa (2021,Phy.Rev.D 103,104069).We analyze the stability of the thin-shell wormhole models under linear perturbations while keeping the cylindrical symmetry and also examine the influence of charge on their stability.The positive quantity of the second derivative of potential at the throat radius might be interpreted as the stability criterion.We find both unstable and stable wormhole solutions for different parameters included in the equation of state and specific forms of considered gravity and illustrate them theoretically as well as graphically.We examine the impact of electric charge on the stability region of a constructed wormhole,which suggests that a wormhole model with a charge may exhibit more stable behavior compared to an uncharged system.

Keywords: wormholes,gravitation,mathematical and relativistic aspects of cosmology

1.Introduction

The wormholes are solutions to field equations of Einstein’s general relativity(GR)and other theories of gravity.They are structural connections in spacetime that link two cosmos or separate sectors of the Universe.Traversable Lorentzian wormholes are geometric structures with a throat connecting two areas of the identical universe or two different universes.The Schwarzschild or Lorentzian wormholes,featuring the boundary on the wormhole mouth,were the inaugural ideas put forth by Einstein and Rosen in[1].The wormholes should always be laced with exotic stuff that deviates from the null energy requirement in the paradigm of GR.By choosing the wormhole’s geometry appropriately,it is possible to reduce the amount of exotic material required across the throat to any desired level,however,it might result in high stresses near the throat.After Morris and Thorne's [2] ground-breaking mathematical investigation in 1988,this topic has acquired a lot of attention.Although a lot of investigation has been done on black holes,particularly to look for signs of a supermassive black hole at the galactic core.This situation is just significantly altered by the new revelation that thin-shell wormholes can replicate recent times demonstrated gravitational ring-down post-merger waves,which were previously thought to be restricted to the black hole horizon.As a consequence,analysis of the stability of thin-shell wormholes is highly critical.Visser’s concept was intended to contain exotic material in a very small area known as a thin shell.Thus,geometrically two manifolds must be cut and pasted together to create a novel manifold that is geodesically comprehensive and contains a shell inserted in the linking region.Within the shell seems to be the unusual material necessary for their preservation,while elsewhere on this shell ordinary stuff may be found.There have been numerous investigations that study the stability of thin-shell wormholes against perturbations while maintaining the inherent symmetries.To establish a thin-shell wormhole,two Schwarzschild models were joined and this was the subject of linearized stability investigation.The researchers investigated the stability of radially perturbed cylindrically symmetrical traversable wormholes featuring the linearized equation of state at the throat [3,4].The f(R) gravitational paradigm is a major modification of the Einstein–Hilbert action,where R is a Ricci scalar.Investigating the Universe’s expansion and evolution,particularly its early-time inflation and late-time growth,has been extensively studied in this gravitational theory [5–13].Even if geometry and matter are on the same level,Einstein’s GR does not account for any conceivable implications associated with a non-minimal connection between geometry and matter.Harko and his collaborators developed f(R,Lm) gravity [14] and f(R,T) [15] theory of gravitation,where R is the Ricci curvature invariant,Lm,i.e.matter lagrangian density and T represents the trace of the stress-energy tensor.Exotic imperfect materials or quantum fluctuations may influence the decision-making process of the stress-energy tensor in the action of f(R,T) gravity.While matter and gravity are inextricably linked,this gravity framework may address the source element.The sample particle’s path deviates from its geodesic trajectory as a result,which may have significant ramifications for cosmic studies.Additionally,modified gravity theories have been used to examine wormhole geometries.The study of thermodynamics,the enigmatic growth of the Universe,gravitational wave phenomena,cosmological packed structures,and dynamical in/stability restrictions with and without electromagnetic interactions have all been done using this expanded form of gravitational theory [16–30].

In any scientific framework,the methods to treat discontinuous surface areas and their characteristics should be taken into account.The junction conditions may establish a link between the compact structural system of the surface and discontinuities of the physical quantity.At the hypersurface Σ,the matching conditions are usually needed to put together strong connectivity across the interior and exterior space-time regions.The most significant contribution to academic frameworks was provided by Lanczos [31],who developed the concept of gravitational matching conditions for a particular hypersurface within the context of GR.These matching conditions were then employed to locate correspondences between several spacetimes.In modified gravity theories,each gravity theory includes its distinctive system of matching conditions that are produced from their equations of motion to address discontinuous surface areas,which incorporate various essential properties (see for more information[32–37]).However,in such gravity theories,the need for the exotic matter stuff may be removed since the matter that makes up the geometry of the wormhole fits the energy conditions and higher-order components of scalar curvature make it easier to create wormholes [38–41].The influence of traversable as well as non-traversable wormholes by choosing numerous types of functions,varying instances by adjusting parametric values of the considered models,and noting how wormhole symmetry performs in these scenarios have all been comprehensively studied in [42–47].The increasing growth of the cosmos breaches the strong energy restriction in GR.Furthermore,modified gravity theories such as f(R,T)gravity have piqued the curiosity of academics,primarily even though they claim to provide a sliver of usable empirical support for faster cosmic evolution [48–51].Bhatti et al[52–54] studied the in/stability of different compact structures with and without electric charge to check the influence of modified gravity theories by using some mathematical techniques under various backgrounds.They [55–57] also checked the relativistic effects upon compact objects and studied the complexity of charged self-gravitating systems in the background of various gravity theories.

Banerjee et al [58] examined wormhole geometries for spherical symmetry and conformal Killing symmetry to improve astrophysical relevance in f(R,T)gravity.Two cases were studied: one with isotropic pressure matter sources,which does not meet wormhole conditions,and the other with an equation of state connecting pressure and density,using phantom energy to violate the null energy condition.They analyzed various physical properties,especially energy conditions,confirming positive energy density from a static observer’s perspective.Graphs supported their findings,and they briefly discussed the volume integral quantifier’s role in understanding exotic matter requirements for traversable wormholes.Banerjee et al [59] studied static,spherically symmetric wormholes supported by matter with isotropic pressure in modified gravity theories.They used various methods to construct solutions meeting wormhole criteria and found examples where matter within the wormhole obeys all energy conditions.They also proposed a transformation to simplify field equations,obtaining more consistent results.These findings suggest specific exact wormhole solutions without exotic matter.The relativistic effects are studied by many researchers with different fluid configurations in the background of modified gravitational theories,one can see for further details [41,60–67].

The universe appears to be expanding more quickly than previously thought,which means that the strong energy criterion must be breached according to GR.There have been several explanations put up for the situation that led to this scenario.Chaplygin gas comprises among them,Chaplygin was the pioneer to establish this model as a model for aerodynamic investigations.It is a perfect fluid with the equation of state ρp=A,where A has a positive constant value.Regardless of the situation of unusual matter stuff,the Chaplygin gas[68]has the feature that the squared sound velocity is indeed positive.Although it had been proposed for phenomenological purposes,rather than cosmological,reasons,this equation of state can be derived via string theory.The notions of exotic stuff that are relevant to astrophysics,for the development of wormholes have recently been taken into account.Some authors have studied the wormholes sustained by phantom energy,utilizing the equation of state p=ωρ,where the parameter involved in this equation of state satisfies the inequality ω<-1.The exotic matter continues to facilitate a wormhole of the Morris-Thorne form in [2].A generalized Chaplygin gas [69,70] with an equation of statehaving two parameters A and γ with conditions A>0 as well as 0<γ ≤1.Therefore,the wormhole metric might have been linked to an exterior vacuum metric to maintain the exotic matter inside a relatively limited zone of space.However,in some kind of a thin-shell wormhole,exotic stuff could be constrained from the outset to the shell at the connecting region,which has already been accomplished with the primordial Chaplygin gas (γ=1) in [71].Consequently,a modified Chaplygin gas model has been put forth in [68] with the paradigm of Friedmann Robertson Walker cosmos.This approach is constructed on the equation of state given below and incorporates an introductory radiation era:It contains three parameters A,B,and γ,where γ is a constant parameter.This equation of state easily reduces to the form p=Aρ,for B=0 and original generalized Chaplygin gas modelfor the case A=0.The current investigation aims to examine charged cylindrically symmetric thin-shell wormholes incorporating the matter in the form of a modified Chaplygin gas under the influence of f(R,T)gravity.In the geometrical formulation of this gravitational theory,we keep investigating the stability of charged static wormhole solutions across symmetry-preserving perturbations.We utilized the ‘cut and paste’ methodology and found both stable and unstable wormhole solutions for the minimally coupled with logarithmic corrections in curvature f(R,T) model,i.e.In this context,the equation of motion at separation hypersurface is obtained by just replacing the derivative of the function f(R,T),i.e.the fRRand fRT,in the general equation provided by Rosa [35] to analyze the construction of thin shell wormhole models and their stable or unstable behavior.The effects of mass,the equation of state parameter,and charge are investigated for the stability of statically charged wormhole models for the greatest possible range of involved parameters.In the framework of this gravity model under consideration,we analyze the stable and unstable static-charged cylindrically symmetric wormhole solutions.

The article is structured as follows: section 2 contains a description of the notations and suppositions that may be utilized in this study.We provide the generalized version of the action integral for f(R,T) gravity and calculate the different components of Lanzos’s equations for thin cylindrical shell matching in the geometric presentation of the theory in the same section.Around the electrically charged static solution at the wormhole throat,the stability analysis is conducted in section 3.The same section will address some additional elements that affect the stability of the investigated fluid configurations and also discuss the constraint formula for wormholes and the minimally associated gravity model.In a corresponding segment,a graphic illustration of the stable/unstable behavior of the studied electrically charged static cylindrically symmetric wormhole formations is shown.We employ the presumption that G=C=1,where C stands for the speed of light and G for the gravitational constant at which all particles gravitate.The discussions and concluding remarks are briefly summarized in the final section 4.

2.Charged wormhole models in geometric representation of f(R,T) Gravity

The basic f(R,T) paradigm and its associated Lanczos equation at separation hypersurface for the construction of wormholes under a specific equation of state will be covered in this section.The following is the generic action of f(R,T)gravitational theory:

in this form of generic action,Lmis the matter lagrangian also k is the coupling constant,i.e.k2=,here G and C demonstrate the gravitational constant and the speed of light,respectively.Furthermore,g and T represent the determinants of the metric gbidefined in terms of xbaccompanied by a signature (-,+,+,+)as well as the trace of the stress-energy tensor Tbi,respectively.Also,f is clearly defined as a generic function of the Ricci curvature invariant and the trace of the stress-energy tensor.In this study we will be used,the Latin indices which cover the range of{0,1,2,3}.We imagine an electrically charged static cylindrically symmetric space-time that has a charged thin cylindrical shell at the junction of the interior and exterior regions.It also assumes that the fluid stress-energy tensor is ideal,i.e.Sηδ=diag (ρ,pθ,pz),where ρ and pφ,pzare surface energy density as well as the surface pressure on the thin shell.The following is a possible formulation for the general static cylindrically symmetric solution under the influence of electric charge:

The radius at which the throat is located can be described by the physical quantity a(τ),where τ represents the appropriate time over the separation hypersurface and a stands for each partial manifold.We defined a unit normal-vector,i.e.ncat hypersurface Σ which is represented in the direction of the interior to exterior space.As a result,f(xb(yη))=0 can be used to represent the separation hypersurface parametric equation.Using this parametric equation,the ncto the hypersurface can be described as follows:

where ncdenotes the unit normal in covariant format,implying that0by definition.Consequently,we conceived a unit four-vector for charged static cylindrically symmetric space-time which can be portrayed as:

The dot represents the derivative with respect to the proper time ‘τ’ all across the analysis of the whole document.For sub-manifolds,the first and second fundamental forms at hypersurface can be defined as:

where xb=(t,r,φ,z) andare non-zero Christoffel symbols of(1).Thus the computation offor metrics in equation (2) are as follows:

where a prime(′) exhibits a derivative with respect to ‘r’.Utilizing the definition as:equation (11)yields:

Using the equation (9) and the constraintwe may obtain:

The Ricci scalar invariant may be expressed as:

Furthermore,the updated gravitational field equation across Σ under the assumption of perfect fluid f(R,T)theory of gravity is determined as follows:

We continue our systematic investigation by assuming the intrinsic stress-energy tensor,i.e.Sηδwhose diagonal entities produce surface energy density(ρ)and surface pressures(pφ,and pz).Here,hηδand [Kηδ] both represent the first and second fundamental form,respectively,at Σ,also ∊has fixed real constant numeric values.Next,we define an alternative expression for the jumping across two different physical values Y over the hypersurface Σ: [Y]=Additionally,utilizing the values of equations (5),(8),(10)and(12)in equation(13),may yield the components of ρ and p at throat radius a as:

in this study p=pφ=pz.Here,it is illustrated how the thin shell model relates to a charged static cylindrically symmetric matching at the hypersurface.For f(R,T)gravity,the first and second fundamental forms must be continuous.Consequently,the six key equations give the complete set of matching conditions for the f(R,T)gravity in the generalized form of matching to a narrow shell over separation hypersurface Σ in geometrical representation,which Rosa’s recently established in [35] as:

In this charged cylindrically symmetric thin shell situation,aforementioned first five matching conditions criteria equations must met,namely: [hηδ]=0,[K]=0,[R]=0,[T]=0,andAdditionally,by plugging the values of equation (11) in (14),we may determine the expression

The equation above demonstrates unequivocally that this is a real scenario since the existence of exotic stuff in wormhole throats is traced by ρ<0.Astashenok [72],added that the equation of state would develop a stable configuration under modified gravity theories,i.e.f(R),f(R,T) gravities.Consequently,stable model construction and dynamical equilibrium may be achieved via various equations of state.A generalized Chaplygin gas [69] with the equation of statetwo parameters A and γ,and constraints A>0 and 0<γ ≤1.There,the wormhole metric may have been coupled to an outside vacuum metric to keep the unusual matter contained inside a relatively small zone of space.Furthermore,novel material may be limited from the start to the shell at the connection sector in some form of the thin-shell wormhole,as has previously been achieved with the primordial Chaplygin gas(γ=1)in[71].As a result,a modified Chaplygin gas scenario with the Friedmann Robertson Walker cosmos has been proposed in[68].This method is based on the equation of state presented below and includes an initial radiation era:

It has three parameters:A,B,and γ,where γ is an arbitrary constant.This equation of state is easily reduced to the form p=Aρ,for B=0 and the classic generalized Chaplygin gas modelfor the case A=0.The proposed study intends to investigate charged cylindrically symmetric thinshell wormholes containing matter in the form of a modified Chaplygin gas under the effect of modified gravity.

3.f(R,T) model and constraint equation

Throughout this sector,the stability of static cylindrically symmetric wormhole solutions underneath the effect of electric charge will be analyzed.This includes evaluating the potential function (V) as well as its first and second derivatives to study the stability across the throat radius a0.It is a key point to keep in mind that the subscript ‘0’ denotes that the quantity under consideration is calculated at the position of equilibrium.In this study,we will examine the charged static cylindrically symmetric thin shell wormhole under specific f(R,T)gravity scenarios having realistic equations of state.A relativistic gravity model comprises variables that have altered and are in line with the facts at hand.The modified gravity theories are therefore investigated in terms of their cosmological feasibility to retrieve a continuous matter dominant period,fulfill solar system tests,and construct stable higher curvature structures capable of reproducing the conventional GR.As a result,considering any option of generic f in the context of f(R,T)gravitational theory,one may acquire a variety of theoretical models that correlate to various matter models,based on the characteristics of the matter origin.Consequently,the general f(R,T) gravitational function can be portrayed in a variety of ways:

• In the first instance of a f(R,T) modified theoretical gravity model,let us suppose that the function f(R,T) is defined as f(R,T)=R+2f(T),while f(T) is a freely chosen function of the trace of the matter’s stress-energy tensor.

• One next looks at the situation for an arbitrary matter source when the function f is defined as f(R,T)=f1(R)+f2(T),where f1and f2are arbitrary functions of Ricci curvature invariant R and trace of stress-energy tensor T,respectively.

• One may also define the action for an arbitrary matter source of f(R,T) gravity being provided by f(R,T)=f1(R)+f2(R)f3(T) as the third type of theoretical model scenario of generalized f(R,T)gravity,where fj,j=1,2,3,are arbitrarily chosen features of the argument.

Let us now assume the scenario of modified gravity for the minimally coupled f(R,T)model with logarithmic corrections in curvature [72] which is worthwhile to study,i.e.

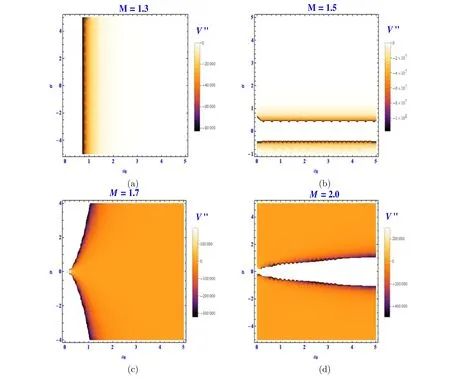
Figure 1.Graphs of V″(a0) relating to different values of mass parameter M=1.3,1.5,1.7,and 2.0,which show the in/stability of our constructed charged static cylindrically symmetric wormhole models provided with some fixed value of charge parameter Q.

Here,we consider a minimally coupled f(R,T) gravitational model that deviates from Einstein’s theory of gravity by effectively generalizing the f(R) theory.This gravitational model might satisfy all local gravity criteria and be considered a suitable tool for examining the stability investigation of relativistic charged or uncharged compact structures.The redial perturbation methodology is used to examine the implications of the f(R,T) model under this study on the development of charged static wormhole model geometry.In this model,the arbitrary constants ‘ξ1,’ ‘β’,and ‘λ’ are used.Additionally,λT is thought to be the correction term to the f(R,T)gravitational theory,whereasare correction term to the f(R) theory.Using λ=0 will simplify our findings and diminish the influence of f(R,T) gravity.Furthermore,GR can be quickly recovered by utilizing ξ1=β=0=λ.Without a doubt,we address the case in which the stable and unstable behavior of the fluid under consideration may be discussed.The following is the presentation of the Ricci curvature invariant for studying the structure of a charged static wormhole around the throat radius:

Now,we calculate how the surface pressure and density of the thin shell relate to each other over the radius a0,which results in the formulae shown below.Thus,the algebraic expressions equations (15) and (18) turn out:

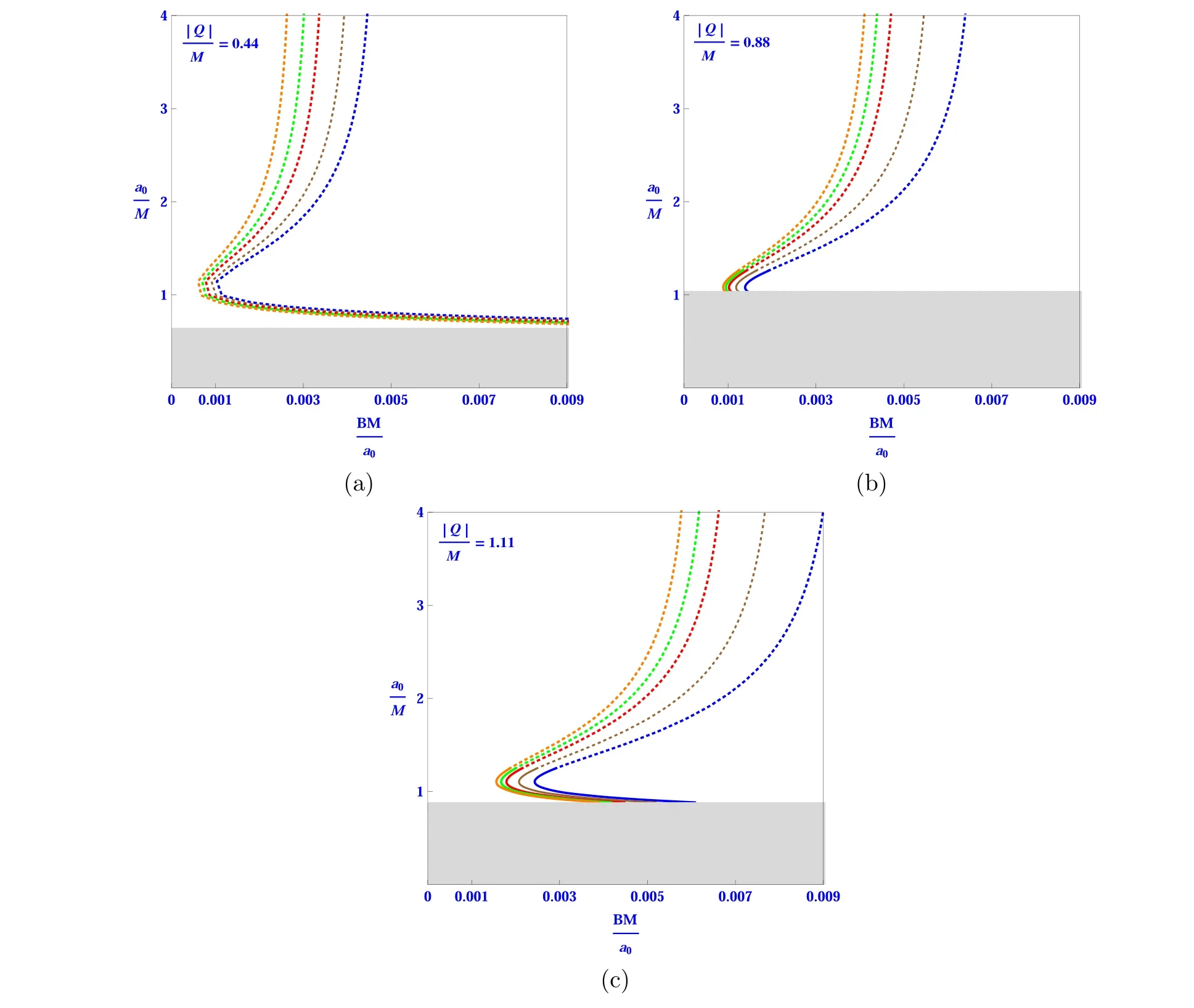
Figure 2.Schematic diagrams of stable and unstable behavior for static cylindrically symmetric wormhole models under the influence of electric charge are shown by a modified Chaplygin gas with fixed value of equation of state parameter as γ=0.44 and the correction parameters to considered modified gravity λ ∊(0.44(blue),0.55(brown),0.69(red),0.95(green),1.0(orange)),in the panels(a),(b),and(c),respectively.The solid plots illustrate static configurations with a throat radius of a0 that are stable solutions,whereas the dotted curves depict the unstable behavior of electrically charged static wormholes with radial perturbations.The fundamental manifold’s horizon radius is greater than the throat radius of the grey sectors,which indicates that the grey areas are unpredictable.

Let us consider the second derivative of the throat radius as a basis for a detailed analysis asalso one may introduceE(a)=to make analysis ease,consequently equation (11) yields

Applying integration,the equation above w.r.t.‘a’ results in

An analytical expression for V(a) at thin shell written as

In this scenario,the potential function is denoted by the symbol V(a);as a result,the equation of V(a) provides the whole dynamic behavior of traversable wormholes.Furthermore,in our instance,the expression for V(a) is presented as

The potential function’s derivative might have the following form:

The expression for F′(a)may obtain from the equation(11)as

In our study,it is easy to confirm that V(a0)=0.Additionally,one may show thatV′(a0)=0by utilizing equation (29) via radial perturbation around a=a0.In the evaluation of the potential at a0,we take the second derivative of the potential

Figure 3.Schematic diagrams of stable and unstable behavior for static cylindrically symmetric wormhole models under the influence of electric charge are shown by a modified Chaplygin gas with fixed value of equation of state parameter as γ=0.77 and the correction parameters to considered modified gravity λ ∊(0.24(blue),0.35(brown),0.59(red),0.75(green),0.9(orange)),in the panels(a),(b),and(c),respectively.The solid plots illustrate static configurations with a throat radius of a0 that are stable solutions,whereas the dotted curves depict the unstable behavior of electrically charged static wormholes with radial perturbations.The fundamental manifold’s horizon radius is greater than the throat radius of the grey sectors,which indicates that the grey areas are unpredictable.

The metric coefficientF,its first and second derivatives at a=a0may be expressed as

By combining equations (31) and (33) in (30),the required outcomes are achieved as follows

It follows that the condition V″(a0)>0 must hold for a wormhole having radius a=a0to be stable.We substitute the values of energy density and surface pressures for the thin shell at a0in EoS which enables us to conceive the constraint equation.Also,we introduce the derivatives of our considered gravitational model at the same stage,i.e.

We obtained the concise form of constructed constraint equation by plugging the values of metric coefficient as F (a0),its derivatives F′ (a0),F″ (a0)and Ricci curvature invariant R(a0) in equation (35) for the charged static case in f(R,T) gravity quadratic in R with logarithmic corrections in curvature is obtained as

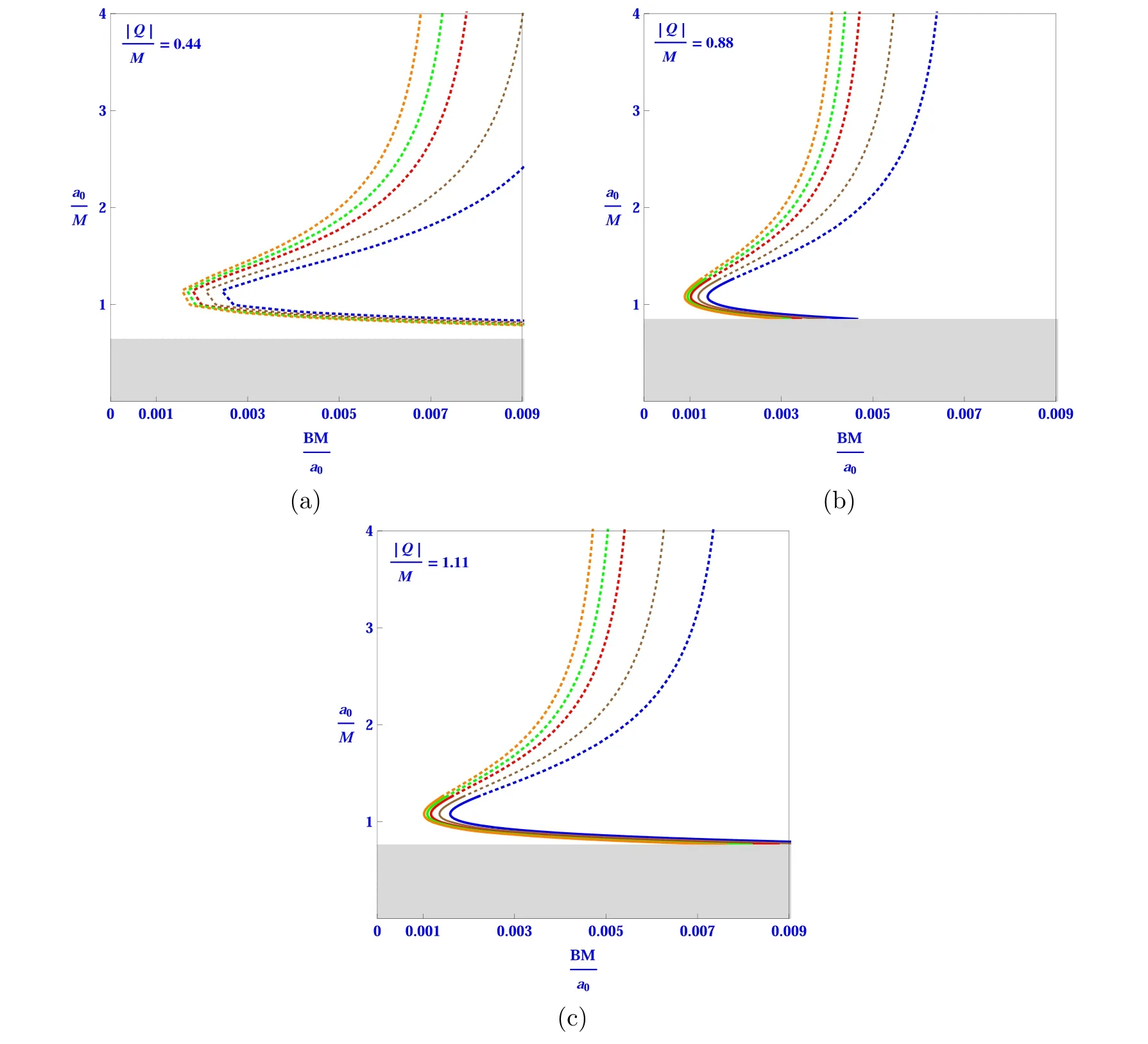
Figure 4.Schematic diagrams of stable and unstable behavior for static cylindrically symmetric wormhole models under the influence of electric charge are shown by a modified Chaplygin gas with fixed value of equation of state parameters as A=0,γ=1 and the correction parameters to considered modified gravity λ ∊(0.14(blue),0.15(brown),0.16(red),0.19(green),0.20(orange)),in the panels(a),(b),and(c),respectively.The solid plots illustrate static configurations with a throat radius of a0 that are stable solutions,whereas the dotted curves depict the unstable behavior of electrically charged static wormholes with radial perturbations.The fundamental manifold’s horizon radius is greater than the throat radius of the grey sectors,which indicates that the grey areas are unpredictable.

The Ricci curvature invariant R(a0) at throat a0turn out:

One may easily verify that the factorwhich appears in equation(35)identically disappears after incorporating the value of metric coefficient F(a0)across the throat radius and also consider the same notion thatThe viable throat radius may be determined using the aforementioned equation with different constants (ξ1,β,η,λ,∊,A,B,and exponents ξ).Since V″(a0) determines whether we possess an un/stable solution for a0radius,we may illustrate this solution via the schematic diagram.

3.1.Graphical analysis

Since the constraint equation is a complicated one,we used graphs to show the charged cylindrically symmetric thin-shell wormhole findings.We arrive at F (rh)=0and F′ (rh)=0,since the charged static solutions rely on critical factors.The critical charge does indeed have a considerable impact on the systems,even though we are working with charged thin-shell wormhole solutions,its effects may be observed in this situation.The solutions to these problems will now beaccumulated and examined.The potential function explains both the unstable and stable structural system of thin-shell wormhole models: if V″(a0)>0 it specifies the stable behavior of constructed models with solid lines,and V″(a0)<0,illustrates the unstable behavior with dotted lines,whereas V″(a0)=0,signifies the unpredictable behavior.The graphs of V″(a0)relating to the varying parametric values of mass M and charge density are subsequently used to show the stability of our system.Also,we illustrate the stable and unstable behavior of our constructed charged static cylindrically symmetric wormhole models with the help of our established constraint equation,consequently in this analysis potential function plays a vital role.In figure 1,we analyze the stable and unstable behavior of static thin-shell wormhole models under consideration for different values of mass and charge.The various EoS parameter (A,γ) and model parameters (ξ1,β,η,λ) combinations are also examined in figures 2 through 4.

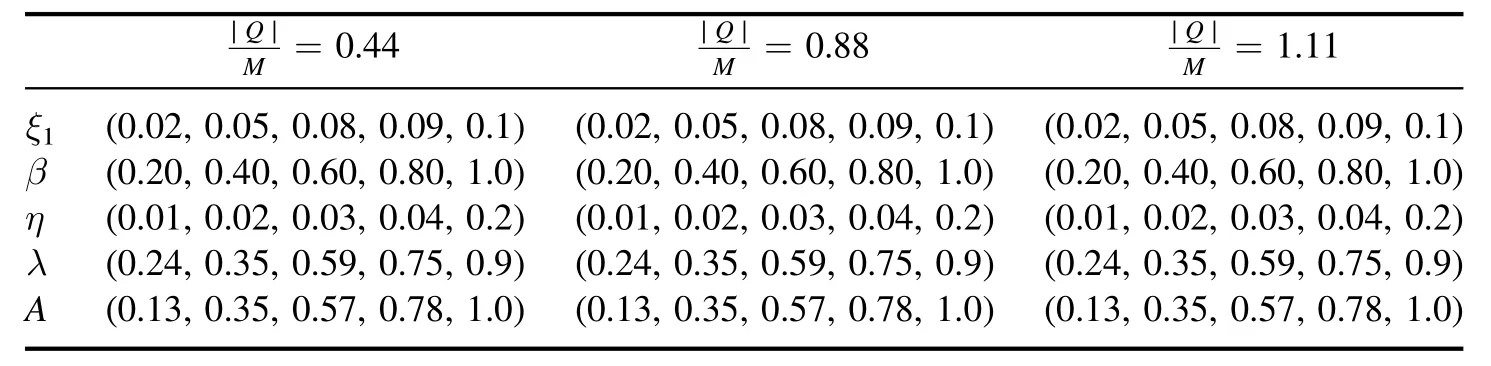
Table 2.Static thin-shell wormhole models under the influence of electric charge with the widest possible parametric values of the model when the modified Chaplygin gas exponent γ=0.77.

Table 3.Static thin-shell wormhole models under the influence of electric charge with widest possible parametric values of the model when the modified Chaplygin gas exponent γ=1 and parameter A=0.

• The schematic diagram in panels (a) and (b),of figure 1 for different values of M=1.3,1.5,respectively,demonstrate only unstable behavior,as the second derivative of the potential function shows a negative value,i.e.V″(a0)<0.

• The graphs in panels (c) and (d) of figure 1 for different values of M=1.7,2.0,respectively,show both stable and unstable behavior as the second derivative of the potential function demonstrates positive as well as negative value,i.e.V″(a0)>0 and V″(a0)<0.

Our analysis explored different scenarios within the framework of modified Chaplygin gas and f(R,T) gravity,varying parameters like charge Q,the gas exponent γ,and correction factors.For specific parametric combinations,the study found unstable solutions in the presence of charge and examined how stable and unstable regions evolved with changes with considered values of different parameters.The results revealed distinct behaviors depending on the values of Q and γ,demonstrating how these factors influenced the stability of the solutions and the sizes of stable and unstable regions within the wormhole geometries.In cases where the charge approached 1 closely,two solutions were observed within a limited range,with stable solutions being shorter and wider.When the charge exceeded 1,two solutions emerged for certain parametric values,with stability regions changing with varying gas exponents.The study also noted that as the charge influence increased,stable regions expanded,and grey zones decreased as the gas exponent increased from 0.44 to 1.

4.Summary and discussion

We examined the effects of f(R,T)gravity on the formulation of wormholes and their stable or unstable behavior.The matching conditions are used to correlate two space-times around the Σ in the geometric representation of considered gravity.Using the fundamental requirements of f(R,T)gravity and thin shell formalizations,we have constructed a charged static cylindrically symmetric wormhole model.For examining the properties of thin shell material and behavior on separation hypersurfaces,the Lanczos equation is extremely helpful.This paper develops charged static cylindrical thin shell wormhole models using the usual cut-and-paste strategy for generic criteria.Consequently,we hypothesized that isotropic perfect fluid accurately characterizes the matter sector,indicating that modified Chaplygin gas supports matter at the shell.It does so because it provides a credible explanation for the Universe’s fast expansion and because it has already been considered in earlier wormhole analysis.Recently,the cosmology has become very interesting in this kind of fluid.For an important gravitational f(R,T)model,we conducted our analysis using logarithmic corrections in R.With the help of some common software,we got some astounding outcomes.In light of this,it is possible to compare the results to those found in earlier studies with the fundamental Chaplygin gas [69].

In this analysis,the constraint equation seems to be complicated,so we used graphs to show the findings regarding our constructed wormhole models.The charge shows the impact on the systems,as we are working with charged thin-shell wormhole solutions,its effects may be observed via graphs.The potential function explains both the unstable and stable structural components of thin-shell wormhole models: if V″(a0)>0,it denotes the stable behavior of constructed models,V″(a0)<0 denotes the unstable behavior,and V″(a0)=0 denotes the unpredictable behavior.The graphs of V″(a0)relating to the varying parametric values of mass parameter M and charge density parameter are subsequently used to show the stability of our system.Also,we illustrate the stable and unstable behavior of our constructed charged static cylindrically symmetric models with the help of our established constraint equation,consequently in this analysis potential function plays a vital role.In figure 1,we analyze the stable and unstable behavior of our constructed static models for different values of mass and charge.We analyzed stable and unstable behavior from figures 2–4 which is summarized as:

• For the assumption that 0 ≤|Q|<1,also |Q| is not very near to 1 and M=1,i.e.Q=0.44 from panels (a) of figures 2–4,only unstable solutions exist when the qualities of the desired modified Chaplygin gas exponent are γ=0.33,0.66,1.0,respectively.It is also worth noting that different values of the correction factor ξ1of the f(R,T) theory of gravity,as well as the parametric values of correction factors in R2,influence the respective areas shown in tables 1–3.

• We also achieve the non-physically significant sector(grey zones).In this case,all unstable solutions are shown by dotted lines which depart fromto go closer toas the gas exponent grows,while grey zones nearly remain the same.We also accomplish the sector with no physical significance (grey zones).In this situation,all unstable solutions are portrayed by dot curves that move away fromto come closer toas the gas exponent increases,and grey zones almost remain same during this similar scenario.

• It follows that there will always be an unstable solution area for an appropriate confined range ofThe throat radiusdecreases in magnitude asincreases,and the original manifold’s horizon radiuscan be produced for large values ofConsequently,in this case of Q=0.44,different curves exhibit nearly similar closeness to each other when different values of the modified Chaplygin gas exponent γ=0.44,0.77,1.0 are evaluated.

• When |Q|≈1 and |Q| get very close value to 1,i.e.Q=0.88 and M=1 from the panels (b) of figures 2–4,one got two solutions for different values of parameters which are illustrated in tables 1–3,for a restricted range of,stable solutions are shorter as well as wider are unstable ones,and also no solution appears beyond this range.

• The solutions curves move away fromand grey zones get short portions with the increasing values of the gas exponent in panels(b)and(c)of figures 2–4 but in panels(a) of similar figures the grey zone almost remains the same.For β=0.66,1.0,the observed stable regions are greater as compared to β=0.33.

• If|Q|>1 and M=1,there are two solutions for different values of parameters for small values of,as shown in tables 1–3.Interestingly,the ranges offor stable and unstable curves change for varying values of γ which is an exponent of modified Chaplygin gas.In this context,the larger one is unstable whereas the smaller one is stable,while no solution emerges outside of a confined range of.For Q=1.11 from the panels(c)of figures 2–4,we got two solutions:the shorter ones are stable,while the larger ones are unstable.The solutions curves move away fromand grey zone depletion with the increasing values of the gas exponent in panels (b) and(c) of figures 2–4 but in panels (a) of similar figures the grey zone almost remains the same.For γ=0.44,0.77,the observed stable zones are smaller as compared to γ=1.

• In the scenario when γ=0.44,0.77,and 1.0,for Q=0.44,0.88 and Q=1.11 the solutions have the almost same behavior.The stable solutions,however,have bigger regions for Q=0.88 than they do in this case when Q=1.11.It is important to note that in every one of the above situations,the stable zones expand as the influence of charge rises and the grey zones shrink as the gas exponent rises from 0.44 to 1.

Finally,One can note that the associated stable or unstable solutions are affected by the values of parameters of the correction terms in the R2of the f(R,T)theory of gravity.As a result,the gravitational model under consideration is cosmologically feasible and meets the local gravity limitations.It is also essential to emphasize that the grey sectors have no physical significance and cannot show us anything about wormhole solutions.In each case,if the relevant mass and charge parametric values are specified for a certain assumed functional form of f(R,T) gravity and constant curvature R(a0),stable or unstable static solutions are always obtained.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

ORCID iDs