Stable bulk nanobubbles can be regarded as gaseous analogues of microemulsions

Changsheng Chen,Hongguang Zhang and Xianren Zhang

State Key Laboratory of Organic–Inorganic Composites,Beijing University of Chemical Technology,Beijing 100029,China

Abstract In our previous work [2022 Phys.Chem.Chem.Phys.24 9685],we used molecular dynamics simulations to show that bulk nanobubbles can be stabilized by forming a compressed amphiphile monolayer at bubble interfaces.This observation closely matches the origin of stability of microemulsions and inspired us to propose here that,in certain cases,stable bulk nanobubbles can be regarded as gaseous analogues of microemulsions: the nanobubble phase and the bubble-containing solution phase coexist with the external gas phase.This three-phase coexistence is then validated by molecular dynamics simulations.The stability mechanism for bulk nanobubbles is thus given: the formation of a compressed amphiphilic monolayer because of microbubble shrinking leads to a vanishing surface tension,and consequently the curvature energy of the monolayer dominates the thermodynamic stability of bulk nanobubbles.With the monolayer model,we further interpret several strange behaviors of bulk nanobubbles: gas supersaturation is not a prerequisite for nanobubble stability because of the vanishing surface tension,and the typical nanobubble size of 100 nm can be explained through the small bending constant of the monolayer.Finally,through analyzing the compressed amphiphile monolayer model we propose that bulk nanobubbles can exist ubiquitously in aqueous solutions.

Keywords: bulk nanobubble,stability,compressed monolayer,three-phase equilibrium

1.Introduction

Bulk nanobubbles (BNBs) are spherical bubbles of submicrometer size,typically 100 nm,suspended in aqueous solution [1–4].Their discovery originated in early studies on ultrasound and cavitation [5],and indirect evidence for the existence of bulk tiny bubbles was then given in a sonar study[6].After 2000,experimental reports on nanobubbles emerged due to the extensive use of advanced experimental techniques,including dynamic light scattering,phase microscopy,infrared spectroscopy and nanoparticle tracking analyzers[7–10].BNBs have aroused strong interest due to their long lifetime and numerous applications,such as water treatment [11–14],agriculture [15,16],biomedicine [17,18]and micro-reactors [19].

The unexpected stability of BNBs seems to contradict classical theory.According to the Epstein–Plesset theory[20],a bubble of radius 100 nm will have an internal pressure about 14.4 times atmospheric pressure and would dissolve within 1 μs.However,experiments reported that the period of existence of observed nanobubbles ranged from several hours to weeks [4,7–10].Such a long lifetime indicates that the reported BNBs are in fact thermodynamically stable.

Obviously,new theories are needed to explain BNB stability.The mechanisms proposed in the last 20 years for BNB stability can be divided into two categories: the enrichment of interfacial charges(zeta potential)[21,22]and the adsorption of contaminants [23,24].Although these models are partly capable of explaining why BNBs are stable,there are some phenomena that cannot be explained by these models: the stability of BNBs at low gas saturation or at zeta potentials close to 0 [25–27] and their almost constant size(∼100 nm) in different reports [26–29].

In detail,for both mechanisms the stable radius of nanobubbles always depends on the number of charges and of contaminants enriched on the nanobubble interface.If the number of charges and adsorbed contaminants changes,stable nanobubbles of any size can be possible.However,the experimentally reported nanobubble size is often around 100 nm [26–29].In addition,both the zeta potential and the contaminant mechanisms[23,24]require the dissolved gas to reach a certain level of supersaturation,which provides an additional pressure (Laplace pressure) to balance the surface tension of bubble interfaces.This requirement is obvious in molecular dynamics (MD) simulations of BNB stability.Weijs et al[30]proposed with MD simulations that diffusive shielding stabilizes BNB clusters.Through MD simulations,Gao et al[31],Hewage and Meegoda[32]and Dixit and Das[33] further analyzed the performance of BNBs at certain levels of gas supersaturation.These studies help us to understand the properties of BNBs.However,the results of these studies still partly contrast with some experimental observations that BNBs remain stable for a long time at rather low gas saturations(S ∼0)[25]as a result of the exposure of nanobubble solutions to the ambient atmosphere.Experiments also show that,at least for certain cases[26]at low gas saturation,the required interfacial charge density and zeta potential for stabilizing BNBs [22] are out of reach.These disagreements demonstrate the existence of some important unidentified characteristics for the stabilization mechanism of real nanobubbles:the stabilization mechanism of BNBs is still an open question.

In our recent work [34],we found that adsorption of amphiphiles (organic contaminants or surfactants) with certain structures can lead to stable nanobubbles.With the dissolution of gas in a large bubble,the areal density of amphiphiles at the bubble interface becomes increasingly high,and correspondingly the surface tension decreases.Once a compressed amphiphilic monolayer is formed,the BNB becomes stable with a vanishing surface tension [34].These findings demonstrate an obvious similarity between BNBs and microemulsions.Microemulsions are known to be thermodynamically stable,with a well-interpreted stability mechanism [35–38].

This similarity inspires us to explore the theory of BNB stability,in analogy with microemulsions.By extending our simulation results [34],in this work we further propose that BNBs can be regarded as gaseous analogues of microemulsions: in nanobubble systems the bubble phase and the solution phase coexist with the external gas phase (see figure 1).We analyze the characteristics of stable BNBs from the following aspects: (i) the similarity between nanobubbles and microemulsions;(ii) shrinking of large bubbles and the adsorption of amphiphilic molecules causing the formation of a compressed amphiphilic monolayer at nanobubble interfaces;(iii)thermodynamic analysis of three-phase coexistence of BNB systems,which is then validated with molecular simulation;(iv) determination of nanobubble size from the rigidity of the compressed amphiphilic monolayer;(v) trace organic contaminants as a source of amphiphiles for the formation of a compressed amphiphilic monolayer.

2.Results and discussion

2.1.The similarity between BNBs and microemulsions

Microemulsions are thermodynamically stable,isotropic liquid mixtures of two immiscible fluids,stabilized by amphiphilic surfactants [35–41].According to the IUPAC definition,a microemulsion is a ‘dispersion made of water,oil,and surfactant(s) that is an isotropic and thermodynamically stable system’[41,42].The typical size of oil-inwater (O/W) microemulsions is close to the experimentally observed diameter of long-lived BNBs (∼100 nm).As schematically shown in figure 1(a),an O/W microemulsion mainly contains three components:solvent(water),surfactant molecules forming the monolayer and oil molecules encapsulated by the monolayer and/or in the excess phase.The whole system is in a coexistence state(Winsor I domain in the Winsor classification) [43]: the O/W microemulsion phase coexisting with an excess oil phase.Such a system exhibits an ultralow interfacial tension,and so far the thermodynamic stability and polymorphic coexistence of microemulsions have been well explained [37–40].

The similarity between BNBs and microemulsions can be summarized as follows.(i) They are both nanoscale entities observed in experiments,with a typical size of ∼100 nm.(ii)Both are thermodynamically stable,although the underlying stabilization mechanism for BNBs [29–32] is still under debate.(iii)Surfactant monolayers on their interfaces play an essential role in their stability.Careful experiments[24]have proved that trace organic contaminants are necessary for nanobubble stabilization,and we further demonstrated that a compressed amphiphile monolayer is required for nanobubble stability at low gas supersaturation [34].(iv) The vanishing interfacial tension would provide a necessary condition for stability,both for microemulsions and for BNBs.For stable BNBs at low gas supersaturation,the vanishing surface tension comes from the dissolution of gas bubbles,which decreases the bubble area until an ultralow surface tension is reached [34].This is again similar to microemulsions.A microemulsion is recognized as a thermodynamically stable object,and the extremely low interfacial tension is the key to its stability.

Based on the aforementioned similarities between BNBs and microemulsions,we further propose that stable BNBs are a special kind of microemulsion,with the oil in the O/W microemulsion simply being replaced with insoluble or slightly soluble gas (see figure 1(b)).Here we will first give the stability mechanism for BNBs;then we will use the mechanism to interpret some strange behaviors of BNBs reported experimentally.

We also need to point out the difference between BNBs and microemulsions:in BNBs the tail groups of surfactants in the monolayer contact gas molecules,while for microemulsions it is oil molecules(figure 1).This difference may lead to different requirements for obtaining ultralow interfacial tension.Regarding the analysis of microemulsion stability,Winsor [44] proposed the so-called R ratio,where ACOrepresents the molecular interactions (per unit interface area)between the tail groups of the surfactant and oil molecules and ACWthose between surfactant heads and water molecules.For microemulsions,ultralow interfacial tension(Rratio=1) can be achieved by changing either ACOor ACW.For BNBs with water–gas interfaces,Rratioshould be rewritten asHere ACG,which comes mainly from tail–tail interactions since the tail–gas interaction is rather weak,is difficult to change.However,ultralow interfacial tension can still be achieved by modulatingACGthrough altering the ionic or steric repulsion between neighboring head groups by various means,such as adding saline solution or co-surfactant.

2.2.The compressed amphiphilic monolayer model and the stabilization mechanism of BNBs

The similarity of BNBs and microemulsions leads us to propose a compressed amphiphilic monolayer model for BNB stability.In this mechanism,we assume that most stable BNBs come from the shrinking of large bubbles,for example microbubbles,as suggested in numerous studies [22–24,45,46].Experimentally,microbubbles can be generated by shaking[47],ultrasound[26,28]and alcohol–water exchange[29].Alternatively,swelling of micelles at high gas supersaturation or macrobubble collapse can also induce microbubbles.Then,at low gas supersaturation the gas dissolution causes the shrinkage of the microbubbles until a compressed amphiphilic monolayer is formed at the bubble interface,which would lead to the formation of stable BNBs (see figure 2).

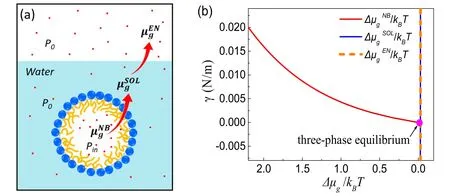
Figure 3.Schematic of three-phase equilibrium.(a)The chemical equilibrium of gas at different phases.are the chemical potentials of the gas inside the bubble,in solution and in the environment,respectively.The chemical equilibrium for gas molecules requires (b)The requiredgas–liquid surface tension for a BNB in mechanical equilibrium with its surrounding as a function of the chemical potential for gas inside the nanobubble,under the conditions of P0 ≈100 kPa and R ≈50 nm.For the purpose of simplification in the figure we assume that the gas in solution and the gas in the environment are in chemical equilibrium,namely,The pink dot indicates the particular situation where the chemical potentials for the three phases are the same,i.e.three-phase coexistence.

During the process of microbubble shrinking,the gradual adsorption of amphiphilic molecules and decrease in bubble area would lead to the interfacial enrichment of amphiphiles for both insoluble and soluble surfactants.For soluble surfactants the enrichment may be because the typical time of surfactant desorption is larger than that for bubble shrinking.The increasing areal density of surfactant at the interface would lead to a decrease in surface tension until a certain value of areal density is reached (see figure 2).Once an extremely low(close to 0)surface tension is reached[34],the compressed amphiphilic monolayer is regarded as being formed.When the monolayer is further compressed,the decreasing average area occupied by each surfactant would become highly energetically unfavorable.Instead,the monolayer can deform in the normal direction (bending) and therefore the interfacial free energy per nanobubble is dominated by the curvature free energy.

2.3.The mechanical and chemical equilibriums of BNBs in three-phase coexistence

In particular cases,the remarkable long lifetime of BNBs is related to the thermodynamic equilibria of different phases:the dispersed BNB phase,the solution saturated with dissolved gas and the ambient gas phase.Therefore,the whole system containing stable BNBs is a three-phase coexistence state.Here we analyze how gas equilibrates in the three phases from the corresponding driving force,i.e.the chemical potential of the gas.We will show that within the framework of the compressed amphiphile monolayer model,both the mechanical and chemical equilibrium of BNBs could be reached,even in a gas-saturated solution.For stable BNBs in such a gas-saturated state we will deduce the vanishing interfacial tension from the quality of three chemical potentials,namely the equality of chemical potentials is the cause and the vanishing surface tension is the result.

The requirement for chemical equilibrium of gas molecules is schematically shown in figure 3(a).Since the partial pressure for solvent is negligibly small inside the nanobubble,only dissolved gas was taken into account here[2,3,20–23].Gas in the nanobubble can be simplified as ideal gas,and the corresponding chemical potentialis

For gas dissolved in solution the chemical potential,is given by

In above equations,P0is the ambient pressure,Pinis the pressure of gas inside the bubble and cgis the actual gas solubility that equilibrates with the bubble.Here a reference state at a pressure Psatis chosen with the gas is saturated in solution,andare the corresponding chemical potential and solubility of the dissolved gas.

Therefore,for a nanobubble in a state of thermodynamic equilibrium,the equality of chemical potential for gas molecules requires

The mechanical equilibrium can be described by the Laplace equationThe Laplace equation,along with Pin=P0,gives rise to an ultralow surface tension(γ ≈0)for stable nanobubbles.Therefore,the vanishing surface tension is a consequence of the thermodynamic (both mechanical and chemical) requirement for stable BNBs.

Note that until now we have not considered the effect of bending energy of the surfactant monolayer.We will demonstrate in a subsequent section that by taking into account the monolayer rigidity,a small but not exactly zero surface tension is sufficient to stabilize BNBs.

2.4.MD simulations validate that three-phase equilibrium can be reached

The three-phase equilibrium coexistence mechanism for a nanobubble system (figure 3(a)) can be verified through MD simulations.Unlike our previous MD simulations for twophase (nanobubble phase and solution phase) coexistence[34],here we considered three-phase equilibrium: a BNB dispersed in a solution coexisting with an ambient gas phase(figure 4).A number of surfactant molecules,H5T3,which are nearly insoluble in solvent,were initially distributed near either the bubble interface or the gas–liquid interface.A given number of gas molecules were inserted into the pre-existing bubble and/or into the gas phase above the solution.The isotropic isobaric ensemble (NPT) was performed at temperature T=0.846ε/kBand pressure P=0.0122εσ−3.The simulation methods and detailed parameters are summarized in the Supplementary Information,and more details can be obtained from our previous work [34].Note that the effect of charge enrichment is not taken into account in our simulations.

The extensive simulation runs demonstrate that the surfactant would rapidly reach the bubble interface and form a surfactant monolayer.In several cases with a sufficient number of surfactant molecules adsorbed on the bubble interface the nanobubble may become stable,although dramatic exchange of gas molecules in three phases and strong shape fluctuation of the bubble are observed.

The typical simulation results are shown in figures 4(a)–(c).Figure 4(c)gives the evolution of the bubble volume over time.The figure indicates that although the bubble volume changes sharply in the initial stage of simulation,the bubble size then fluctuates around a constant size,demonstrating that the nanobubble has reached both mechanical and chemical equilibrium with its surroundings.We also simulated different cases with various numbers of surfactant molecules.The simulation results(see,e.g.,figures 4(d)–(f))show that adding more surfactant would lead to extra adsorption of surfactant at the flat gas–liquid interface,while the BNB remains stable.In general,both cases in figure 4 validate the three-phase coexistence mechanism for stable BNBs displayed in figure 3(a).

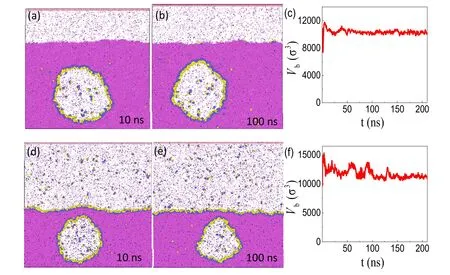
Figure 4.Verifying the three-phase equilibrium with MD simulation.(a),(b) Two typical snapshots for a BNB fully covered by H5T3surfactant molecules.(c) The time evolution of the bubble size.In this case,the numbers of surfactant,liquid and gas molecules added are 492,121 848 and 768,respectively.(d)–(f) A different situation in which both the bubble and the flat gas–liquid interface are covered by H5T3 surfactant molecules.In this case the numbers of surfactant,liquid and gas molecules added are 1092,162 936,and 1952,respectively.

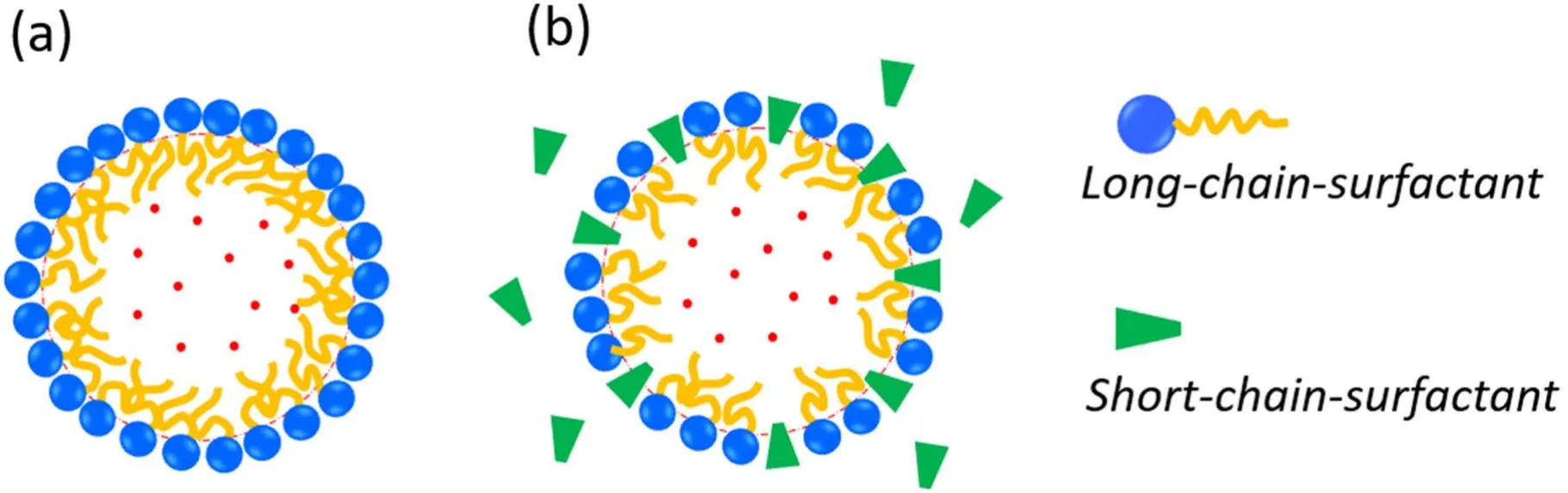
Figure 5.Schematic drawing of two different models for the compressed amphiphile monolayer: (a) the monolayer comprises only longchain-surfactant molecules and (b) the monolayer contains both long-chain and short-chain surfactant molecules.

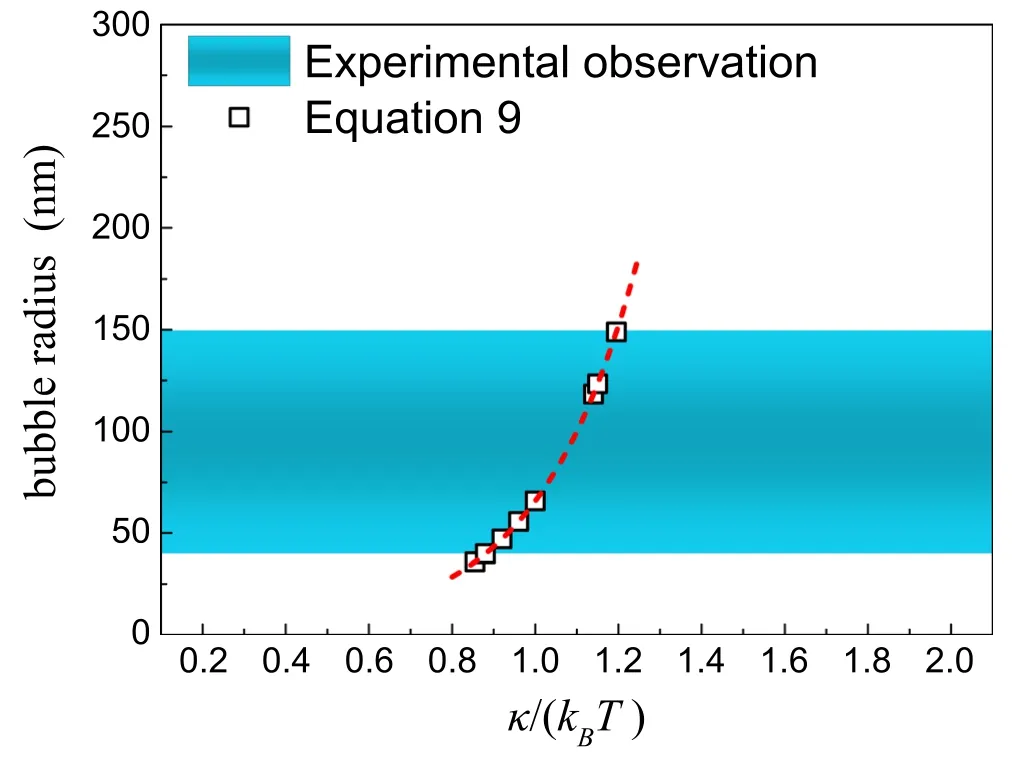
Figure 6.Comparison of predicted nanobubble radius(equation(9))with the range of radii of stable nanobubbles reported experimentally.The symbols indicate the predicted bubble sizes with the stiffness k given in literature [37–39,48–51].The shaded areas indicate the size range of stable BNBs observed experimentally.

For the stable nanobubbles obtained,we also extended the simulation time to 300 ns.As expected,coexistence of the three phases continued (see figures S2(a)–(b) in the SI).The figures clearly show that the nanobubbles are still stable.

2.5.Nanobubble size can be estimated from the rigidity of the compressed amphiphile monolayers

We now turn to the question of why the typical size of BNBs observed experimentally is around 100 nm.First,we stress again that once a compressed amphiphilic monolayer is formed it shows a tendency to resist certain changes in its curvature.This is because,for the compressed monolayer,further decrease in the monolayer area would become energetically unfavorable.In contrast,a compressed monolayer can deform more easily in the bending mode and thus the interfacial deformation of the nanobubble is dominated by the curvature free energy.This curvature energy for a tensionless monolayer with a curvature that deviates from its spontaneous curvature was emphasized by Helfrich[48].Accordingly,the interfacial free energy of the surfactant monolayer reads

in which k is the bending rigidity,is the saddle-splay modulus and f0is the interfacial tension of the surfactant monolayer without considering bending energy [49].The spontaneous curvature,c0=1/R0,with R0the spontaneous radius of curvature,reflects the asymmetry between the inside and outside of the monolayer.For a spherical nanobubble,the actual curvature c1=c2=1/R,and thusFs=Here,the interfacial energy of the planar surfactant monolayer per unit area [49].When the surfactant monolayer is flat,the actual curvature c1=c2=0 and the interfacial free energy of the surfactant monolayerFs=∫γ0dA.

The spontaneous curvature c0and the bending stiffness k of surfactant monolayers are important factors that determine nanobubble size.k can decrease strongly once mixtures of surfactants of different chain lengths are introduced because of the resulting disorder of surfactant chains [50].Szleifer et al [50] found that for a one-component surfactant membrane k increases from kBT to tens of kBT by increasing the chain length or decreasing the area per surfactant molecule.They also demonstrated that addition of relatively short-chain alcohol or other co-surfactant additives is sufficient to lower the bending constant by an order of magnitude.Based on these findings [50],we suppose that there exist different situations for a compressed amphiphilic monolayer of BNBs depending on the experimental conditions (see figure 5).

For the first case (figure 5(a)),for which a single type of large and insoluble surfactant comprises the monolayer,the stiffness k of the compressed monolayer for BNBs is rather large (k >>1kBT) [38,51].With equation (6),the minimization of Fswith respective to bubble radius at constant total area A (or equivalently,the fixed number of surfactant molecules at the nanobubble interface) gives the optimal bubble radius Rewith [38,51,52]

Therefore,for a stiff monolayer(k>10 kBT),the minimized bending free energy Fswill force the equilibrium size of the nanobubble to approach R0becauseis relatively small[39,40].In other words,it is the spontaneous curvature c0=1/R0that determines the size of BNBs.c0or R0can be directly related to the packing parameter of amphiphilic molecules,indicating the tendency of the interface to curve toward either the water(c0>0)or the gas(c0<0).As shown in our MD simulations [34],c0<0 is required for stable nanobubbles.

The second situation is for a multicomponent amphiphilic monolayer (figure 5(b)),in which the mixing of longchain and short-chain surfactants (e.g.alcohol) substantially lowers the bending constant k [50].We believe that this situation represents BNBs stabilized by trace organic contaminants.When k is small enough(kBT),it is the stiffness of monolayer k rather than spontaneous curvature that dominates the observable bubble size.In this case,the competition between thermal and bending energies can be described by the notion of persistence lengthξk,which plays an essential role in determining nanobubble size,as for microemulsions[38–40,53].

Following Helfrich [53]and Peliti and Leibler [49],we assume that a stable nanobubble would reach its actual size R≈ξkwhen the effective stiffness keapproaches zero.The effective stiffness is determined by [49]

withξ0the molecular length close to the surfactant layer thickness and wave number q (with ξk∼q-1) in the thermal fluctuation process.For nanobubbles with a soft monolayer,equation (8) leads to

Note that a similar equation was given for microemulsions[53],with 4π/3 replaced by 2π [38,51].Here we determine bubble ξkfor BNBs by setting the typical stiffness of flexible surfactant monolayers around 1kBT [50],i.e.k ∼kBT.When we choose the typical values for a surfactant monolayer,ξ0～ 10Å[38–40] and k ∼1kBT [50],equation (9) givesξk≈65.8 nm.Thus,the bubble size predicted from the compressed amphiphilic monolayer model is roughly consistent with the experimentally observed values that are mostly around 100 nm (diameter) [24,25].

For flexible amphiphilic monolayers,the typical stiffness k reported experimentally is close to 1kBT,i.e.0.8–1.2 kBT[38–40,50–52].With equation (9),we can therefore predict the size of a stable BNB (figure 6).The range of predicted bubble radii is consistent with those from experimental observations (about 40–150 nm) [24–29].

If the stiffness k of the monolayer is further reduced,k is much smaller than kBT.ξkis of the order of a molecule's length.In this case,well-defined surfactant monolayers become unstable due to the dominant shape and thermal fluctuation.Thus,the nanobubble structure becomes unstable and one would obtain a micelle-like structure [34].

In general,we distinguish two different situations,both leading to compressed amphiphilic monolayers that can stabilize BNBs.The first corresponds to a one-component rigid monolayer.In this case,the bulk size is mainly controlled by the spontaneous radius of curvature,R0,which is directly related to the packing parameter of amphiphilic molecules.The second situation corresponds to a multicomponent soft monolayer,which is featured with a lower bending constant,k ∼kBT.In this case the bubble size would be around 100 nm.In case of k<

2.6.The ubiquitous existence of BNBs in aqueous solutions

Here we focus on an open question for the compressed amphiphile monolayer model: where do the amphiphilic molecules come from?First,we will illustrate that even trace organic contaminants in solution can provide amphiphilic molecules to stabilize BNBs.Then we propose that BNBs can exist ubiquitously in aqueous solutions.

A careful experimental work [24] shows that concentration of the generated BNBs becomes negligible if various source of contaminants are properly avoided.This clearly indicates that trace organic contaminants are necessary for nanobubble stabilization.However,at present it is still difficult to avoid contaminants completely: they may come from the gas source,from exposure of the solution surface to airborne contaminants,from the contacting solid or from the solution itself.

Here we just illustrate that even a small quantity of trace organic contaminants dissolved in a so-called‘pure’solvent is sufficient to supply the amphiphile molecules for stabilizing a large number of BNBs.To analyze whether this small level of contaminants is sufficient to stabilize the BNBs we take the radius of the nanobubble as R=50 nm and assume that the cross-sectional area a of the surfactant molecule is about 9 Å2,which is close to the values reported in the literature[54–58].For a single nanobubble of 100 nm,the number of surfactant moleculesn1required for the compressed monolayer can be estimated asThe total number of surfactant molecules needed for all BNBs in 1 ml of solution is aboutN1=n1cNB≈3.49×1 013.Here the typical concentration of BNBs,cNB∼108ml–1,was used [26–29].

Then we roughly estimated the amount of surfactant existing in the solution from the reported carbon content(TC),which mainly comes from organic contaminants in the solution and acts as a surfactant.In nanobubble experiments the TC of pure water is often given,with a typical value of<50 parts per billion (ppb).Here we can approximate the concentration of surfactants (contaminants) in water,csurf,by a typical TC value of 24 ppb [59].The total number of surfactant molecules N2actually contained in 1 ml of water can be estimated byHere Msurfis the molar mass of the surfactant,having a value of 288 g mol−1with reference to sodium dodecyl sulfate,and NAis the Avogadro’s constant.If we assume that 60%of the TC consists of surfactants,=N2× 60%≈3 × 1013.It is clear thatmeaning that even the ultrapure water used in experiments still contains a sufficient quantity of contaminants to stabilize BNBs with a typical nanobubble concentration of cNB≈108ml–1.

Note that this is just a rough estimate,without considering the distribution of the organic contaminants between dissolution and the nanobubble interface.If the distribution is taken into account,the concentration of stable BNBs would decrease.This agrees with the experimental observations that nanobubble concentration would substantially reduce if the solution was carefully prepared to remove different sources of organic contaminants [24].However,the trace organic contaminants dissolved in the solution itself are not the only source of amphiphilic molecules.They may also come from,for example,exposure of the solution surface to airborne contaminants and the container.Several reports have demonstrated that graphite surfaces exposed to air may accumulate a thin organic layer[60–62].Regardless of where they come from,organic contaminants and other factors have been used to interpret the stability and behavior of interfacial nanobubbles [63–66].

When there is surfactant adsorption,the compressed amphiphilic monolayer model allows us to anticipate the ubiquitous presence of BNBs in some aqueous solution,with a greater or lesser bubble concentration.This ubiquity is based on the following facts: the unavoidable presence of trace organic contaminants may act as a source of amphiphiles;adsorption of amphiphiles and shrinking of large bubbles leads to the formation of a compressed amphiphile monolayer;and BNBs with such a compressed monolayer are thermodynamically stable in some cases.Therefore,we can conclude that the appearance of BNBs may be much more common than we expected,in particular in an aqueous solution exposed to the ambient atmosphere.

3.Conclusion

The stabilization mechanism of BNBs is still an open question.Based on our discovery of the existence of a compressed amphiphilic monolayer on stable nanobubbles [34],in this work we further proposed that BNBs can be regarded as gaseous analogues of microemulsions: the nanobubble phase and the bubble-containing solution phase coexist with the external gas phase.This three-phase coexistence was subsequently validated by MD simulations.The stability mechanism for BNBs is given as follows.The shrinking of large bubbles and adsorption of amphiphiles lead to the formation of a compressed amphiphilic monolayer at nanobubble interfaces.The compressed monolayer has an ultralow surface tension,and thus it is the curvature free energy,rather than surface tension,that dominates the interface free energy and nanobubble stability.

In the presence of surfactant adsorption,with the compressed amphiphilic monolayer model,we can interpret two mysterious experimental observations: the stability of BNBs at low gas saturation and stable nanobubbles often having a typical size of around ∼100 nm.For the first observation,the unexpected stability of BNBs at rather low gas saturations can be well interpreted by the ultralow surface tension of nanobubbles.Due to the formation of a tensionless amphiphilic monolayer,gas supersaturation is no longer a necessary condition for stability of BNBs.We also explained why the typical reported size of stable BNBs is often around 100 nm.We proposed that most experimentally reported BNBs are stabilized by adsorbed trace organic contaminants,the multicomponent nature of which leads to a very low bending constantkof the formed monolayer.Under conditions of k ∼kBT,a simple estimate from persistence length predicts a stable nanobubble size of around 100 nm.

We also suggest that BNBs can exist ubiquitously.We show that even the small amount of trace organic contaminants dissolved in chemically ‘pure’ solvent is sufficient to supply the amphiphilic molecules needed for stabilizing BNBs at a typical nanobubble concentration cNB∼108ml–1.In real situations,there are many more sources of organic contaminants that can stabilize BNBs.Therefore,the ubiquity of BNBs is a direct consequence of the compressed amphiphilic monolayer model: unavoidable existence of trace organic contaminants that act as a source of amphiphiles,and the interface adsorption of amphiphiles;shrinking of large bubbles that lead to the formation of a compressed amphiphilic monolayer;and the BNBs with such a monolayer being thermodynamically stable.The ubiquity of BNBs in some aqueous solutions may have significant effects on a variety of processes that are related to bubble formation and disappearance.

The stability mechanism presented here might offer guidelines for studying stable BNBs experimentally.(i) We can take inspiration from the extensive experimental study of microemulsions because of the similarity of stability mechanisms between nanobubbles and microemulsions.(ii)Pre-existing large bubbles (either microbubbles or macrobubbles)are essential for the generation of stable nanobubbles because nanobubbles come from the shrinking of large bubbles—spontaneous nucleation of nanobubbles seems unlikely at low levels of gas supersaturation.(iii) The simultaneous addition of both surfactant and co-surfactant may be more effectively in stabilizing nanobubbles.(iv)The elimination of nanobubbles requires control of the introduction of trace contaminants not only from water but also the ambient environment,and the instrumentation and electrophoretic removal of pre-existing charged nanobubbles if necessary.

Our findings offer a theoretical foundation for the stability of BNBs,but reliable experimental validation is needed to establish their existence.Additionally,it is important to note that the proposed model and the zeta potential model are not necessarily incompatible.Although we do not include the impact of enriched charges on the BNB interface in our model,this does not mean that the zeta potential does not play an important role in nanobubble stability.In fact,we think the two mechanisms should work in concert with one another,at least in some circumstances.

Acknowledgments

The work was supported by the National Natural Science Foundation of China (Grant Nos.21978007 and 22278013).

ORCID iDs