The influence of a self-focused laser beam on the stimulated Raman scattering process in collisional plasma

Keshav Walia and Taranjot Singh

Department of Physics,DAV University Jalandhar,India

Abstract The influence of a self-focused beam on the stimulated Raman scattering (SRS) process in collisional plasma is explored.Here,collisional nonlinearity arises as a result of non-uniform heating,thereby causing carrier redistribution.The plasma density profile gets modified in a perpendicular direction to the main beam axis.This modified plasma density profile greatly affects the pump wave,electron plasma wave(EPW)and back-scattered wave.The well-known paraxial theory and Wentzel–Kramers–Brillouin approximation are used to derive second-order ordinary differential equations for the beam waists of the pump wave,EPW and the scattered wave.Further to this,the well-known fourth-order Runge–Kutta method is used to carry out numerical simulations of these equations.SRS back-reflectivity is found to increase due to the focusing of several waves involved in the process.

Keywords: self-focusing,back-reflectivity,back-scattered beam,electron plasma wave,nonuniform heating

1.Introduction

In recent years,technological advancement has led to the production of intense lasers with intensities exceeding 1018W cm-2[1,2].Several researchers have been investigating the interaction of intense lasers with plasmas due to its applicability to distinct applications,such as inertial confinement fusion,particle acceleration and relativistic nonlinear optics [3–15].Success can be achieved in these applications on the basis of deeper laser beam transition through plasmas.The interaction of lasers with plasma causes the generation of many nonlinear phenomena,including selffocusing,filamentation and scattering instabilities.Laser–plasma coupling efficiency is greatly reduced as a result of these nonlinear phenomena [16–24].Therefore,experimental/theoretical research groups are working on these instabilities so that laser–plasma coupling efficiency can be improved.Out of the various instabilities mentioned above,a crucial role is played by scattering instabilities,such as stimulated Raman scattering (SRS) and stimulated Brillouin scattering (SBS),as they cause a reduction in the coupling efficiency of laser–plasma interaction.The input beam is split into an electron plasma wave (EPW) and scattered wave in the SRS process.The relativistic electrons are produced due to this EPW;there is also the possibility of the target core being preheated due to these relativistic electrons.The information regarding the wasted energy is obtained through the scattered beam.Therefore,Raman reflectivity is basically useful for getting the information of useful and dissipated energies in laser–plasma coupling.

A literature survey has already confirmed that the past research work on SRS was explored through the concept of plane waves.If a pump beam with non-uniform irradiance is taken,then a phenomenon like self-focusing becomes dominant.Many other nonlinear processes,including SRS,SBS and electrostatic waves,are strongly affected due to the selffocusing phenomenon.Therefore,the consideration of selffocusing is an essential requirement while exploring the SRS process in laser-driven fusion.Many researchers have already explored the interplay between scattering instabilities and self-focusing[25–34].Barr et al[35]explored the growth rate of SRS while incorporating the self-focusing phenomenon.Rozmus et al [36] explored the generation of thermal electrons through EPWs in the SRS process.Bulanov et al [37]explored the interplay between self-focusing in the SRS process in underdense plasma.Tzeng and Mori explored the inter-connection between SRS and self-focusing [38].They also found that the SRS process causes suppression of both cavitation and self-focusing.The effect of self-focusing on SRS has also been explored by Russell et al[39].Fuchs et al[40]explored the growth of SRS under distinct conditions via variation in suitable laser–plasma parameters.Mahmoud and Sharma [41] explored the impact of self-focusing and pump depletion on the SRS process.In their work,they followed the approach of modified Raman gain.Rose et al[42]found that Landau damping associated with electrostatic waves gets increased due to the small density of superthermal electrons.Matsuoka et al [43] explored the formation of filaments via particle in cell (PIC) simulations and further investigated the correlation between these filaments and the SRS process.Many researchers have also explored the impact of selffocusing on the SRS process in different plasma environments.The incitement of the current study is to explore the self-focusing effect on SRS in collisional plasma.

The present work explores the effects of a self-focused intense beam on SRS in collisional plasma.The pump wave(ω0,k0)interacts nonlinearly with the pre-excited EPW(ω,k),resulting in production of a back-scattered wave(ω0-ω,k0-k).Here,we have considered(k≈ 2k0)as a special back-scattering case.The nonlinearity in the dielectric function of plasma is created as a result of non-uniform heating of carriers.This further leads to focusing of the input wave.There is also a change in the dispersion relation for the EPW,and focusing of the EPW is observed under special conditions.As the intensity distribution of the input wave and EPW is linked with the back-scattered wave,enhanced backreflectivity is found with the focusing of waves.The wellestablished approximations,namely,paraxial approximation and Wentzel–Kramers–Brillouin (WKB) approximation,are utilized to derive nonlinear ordinary differential equations(ODEs)for the beam waists of distinct waves involved in the process and SRS back-reflectivity.The present paper is structured in three sections: in section 2,second-order ODEs for the beam waist of the EPW are set up.In section 3,second-order ODEs for beam waists of the input wave,scattered wave and the expression for SRS back-reflectivity are set up.A discussion and conclusions are presented in sections 4 and 5,respectively.

2.Wave equation solution for the EPW

The high-power beam with angular frequencyω0and a propagation vectork0is assumed to be propagating in unmagnetized plasma.Suppose the direction of the propagation of the beam is along the z-axis.Initial irradiance distribution associated with such a beam is represented as

In the above equations,r0,c,ε0andrdenote the initial beam radius,the speed of light,the linear part of the dielectric function and the radial coordinate of the cylindrical coordinate system,respectively.One can express the modified electron concentration for collisional plasma as [44–46]

In equation (3),the various types of collisions existing in collisional plasma are governed through parameter .χIfχ=-3,then collisions between ions and electrons are dominant.Ifχ=2,then collisions between electrons and diatomic molecules are dominant.Ifχ=0,then collisions are dependent on speed.In equation (3),the nonlinearity coefficient ‘α’ is denoted asHere,N0,e,m,KBandT0correspond to the number density in the beam’s absence,electronic charge,electronic mass,Boltzmann’s constant and the temperature of plasma in equilibrium,respectively.In the hydrodynamic approach,the motion of plasma particles can be described through the following fluid equations [47]

(1) Equation of continuity

(2) Equation of motion

(3) Poisson’s equation

In the above equations.,Ncorresponds to instantaneous electron density,whileVandPdenote the speed of electron fluid and pressure,respectively.Here,we have takenγ=3,which is the ratio of specific heats,andΓ is the Landau damping factor.By using a perturbation approach and further following standardized techniques,one can write the equation for electron density variation as

Following [44–46],the solution of equation (7) may be expressed as

In equation (8),ωdenotes angular frequency,kdenotes the wave vector for the EPW andSdenotes the eikonal for the EPW.Further,one can write the dispersion relation for the EPW as

Now,put equation(8)in equation(7)and equate the real and imaginary parts separately,

Following [44–46],the solution of equations (10) and(11)is represented as

In equation (12),the damping factor is denoted byki.The beam waist for the EPW is denoted byf‘’and it satisfies the following differential equation

The boundary condition isf=1 andatz=0.Further,f0andr0denote the beam waist and initial radius of the beam for the input beam.(cf equation (21)).

3.Wave equation solution for the pump wave and scattered wave

We know that the total electric field (ET)is the addition of fields due to pump wave (E)and scattered wave(Es)

The wave equation for the field vectorETmay be expressed as

In equation (16),the total current density is expressed asJT=NeV.By equating 0th-order and first-order terms,one can get

In equation (18),the complex conjugate ofnis *n.We have ignored the pump depletion in equation (17).This is because there is a depletion in energy due to pump depletion,which produces a major impact on the self-focusing of various waves involved and SRS reflectivity.Further,to solve equation (18),we ignored the term ∇(∇ ∙E)in comparison to ∇2Es,assuming that the scale length of change in the dielectric function in the radial direction is greater than the wavelength of the main beam.Also,we can say thatr0≫2π/k0.These approximations are actually helpful for mathematical simplicity.Following [44–46],one can write the solution of equation (17) as

In the above equations.,f0denotes the beam waist for the input beam,and the differential equation satisfied by it is mentioned below;

Now,the solution of equation (18) is mentioned below

Upon putting equation(22)into equation(18)and further e quating terms with the same phases

Equation (24) has a solution of the form

By substituting equation (25) into equation (24),further ignoring space differentials,one can get

Further,equation (23) has a solution of the form

Using equation(27)in equation(23)and further equating real terms and imaginary terms separately,

Following [44–46],the solution of equation (28) and (29)may be written as

In the above equations,bandfsrepresent the initial radius and beam waist of the back-scattered beam.Further,the differential equation satisfied byfsis given below;

The initial conditions are dfs/dz=0andfs=1atz=0.To obtain the value ofB1,let us assume thatEs=0atz=zc,i.e.

Atz=zc,the amplitude of the scattered wave is zero,i.e.

Now,one can express SRS back-reflectivity as,

4.Discussion

The second-order ODE for the beam waistsf,f0andfsof an EPW,main beam and scattered beam are expressed by equations(14),(21)and(32),respectively.It is not possible to obtain an analytical solution of these equations.Therefore,these equations are numerically solved for established laser–plasma parameters;

In all these three equations,the first term causes a diffraction phenomenon,while the second term causes convergence of the beam.The dominance of the first term in each equation causes diffraction of the beam,while dominance of the second term causes convergence of the beam.When both terms of each equation balance each other,then neither convergence nor diffraction takes place and the beam goes into self-trapped mode.

The impact of the intensity of the laser beam on the beam widthsf0,fandfsof the pump wave,EPW and scattered wave is shown in figures 1,2 and 3,respectively.The black,red,and green curves represent2.0,2.5 and 3.0,respectively.The beam widths of each beam get shifted towards higherηwith a rise in theparameter.The focusing behavior of these waves is reduced with a rise invalues.This is due to the supremacy of the divergence term in comparison to the convergence term at largervalues.

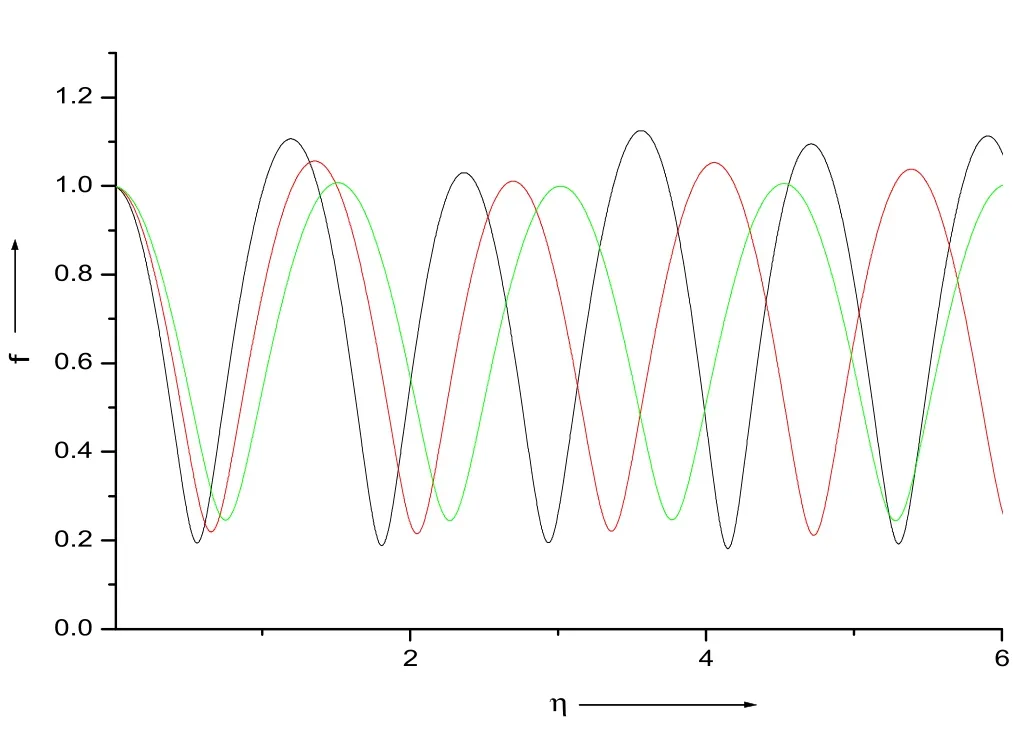
Figure 2.The impact of the intensity of the laser beam on the beam width f of the EPW.The black,red,and green curves represent=2.0,2.5 and 3.0,respectively.

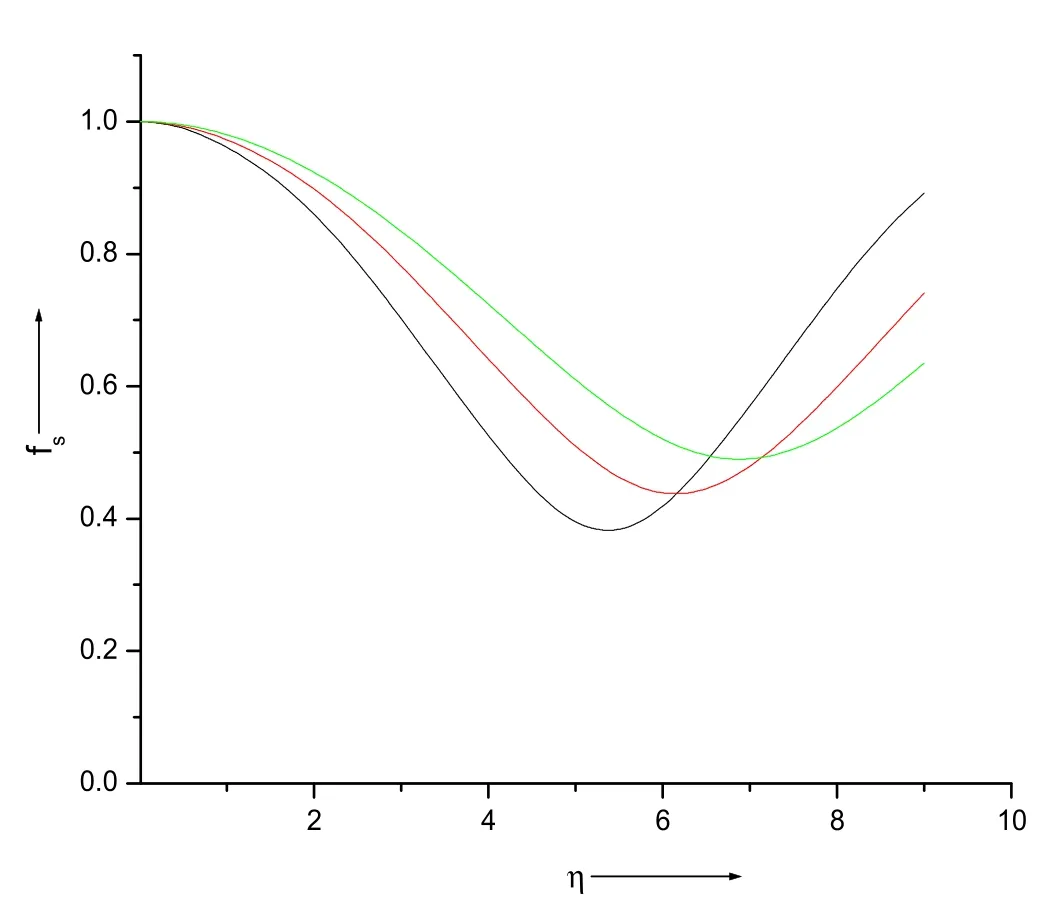
Figure 3.The impact of the intensity of the laser beam on the beam width fs of the scattered wave.The black,red,and green curves represent=2.0,2.5 and 3.0,respectively.

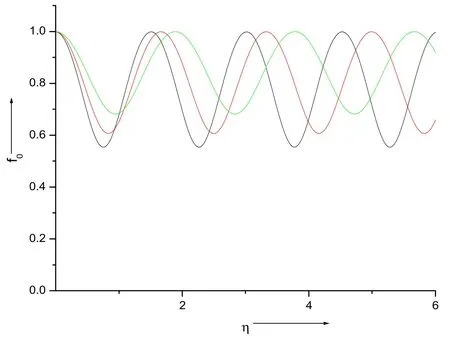
Figure 4.The impact of the density of plasma electrons on the beam width f0 of the pump wave.The green,red and black curves represent =0.15,0.20 and 0.25,respectively.

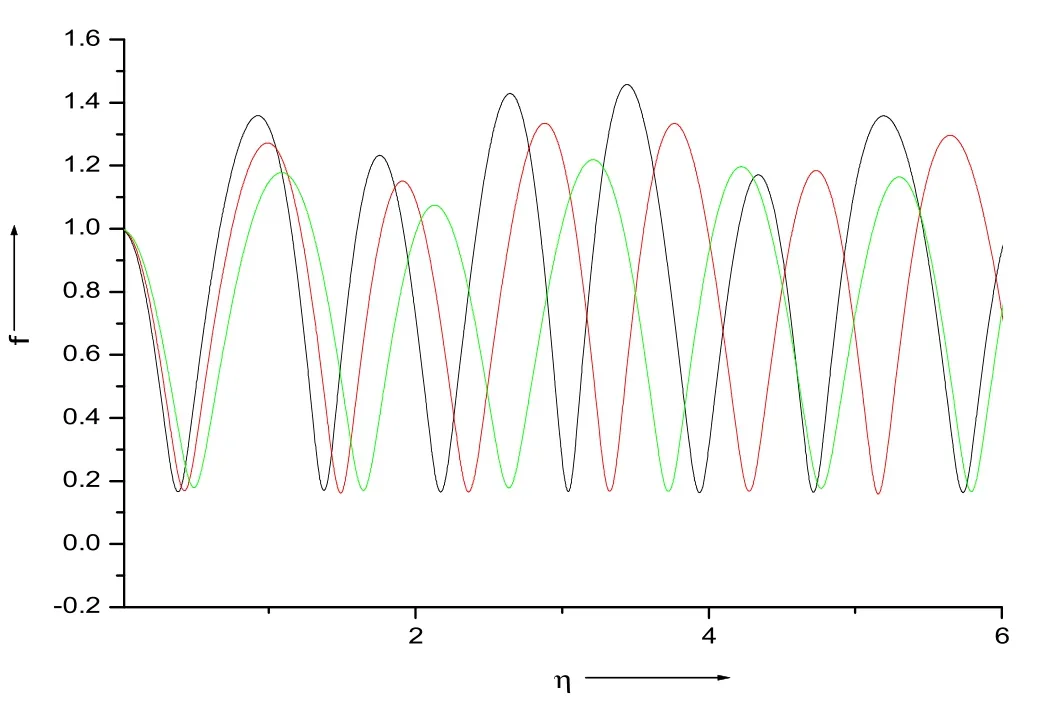
Figure 5.The impact of the density of plasma electrons on the beam width f of the EPW.The green,red and black curves represent=0.15,0.20 and 0.25,respectively.

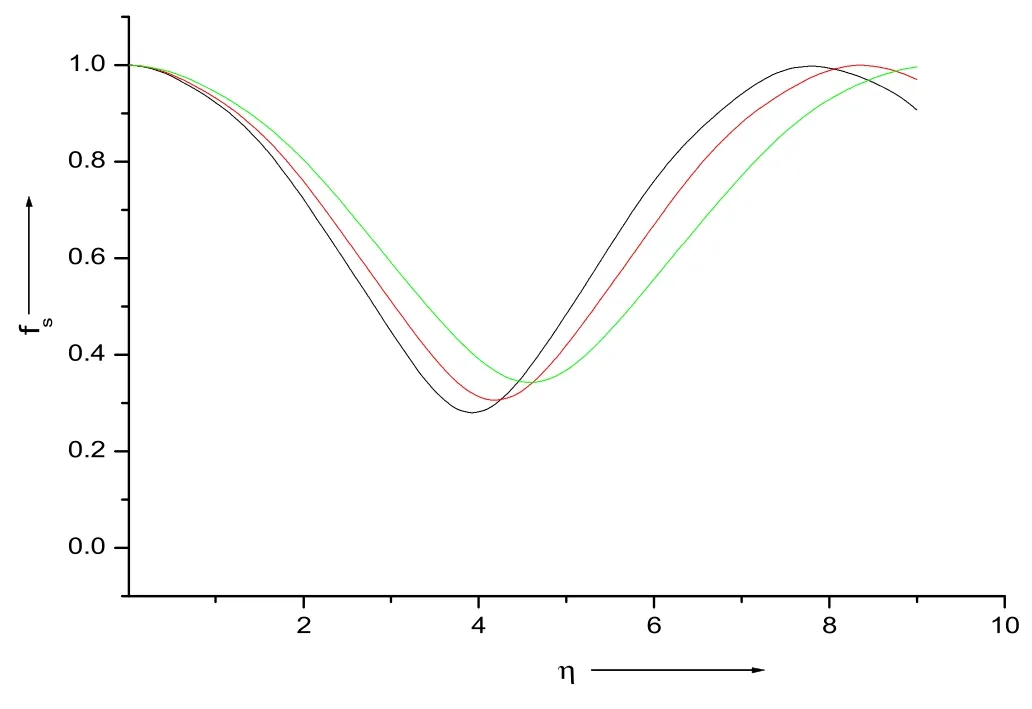
Figure 6.The impact of the density of plasma electrons on the beam width fs of the scattered beam.The green,red and black curves represent =0.15,0.20 and 0.25,respectively.

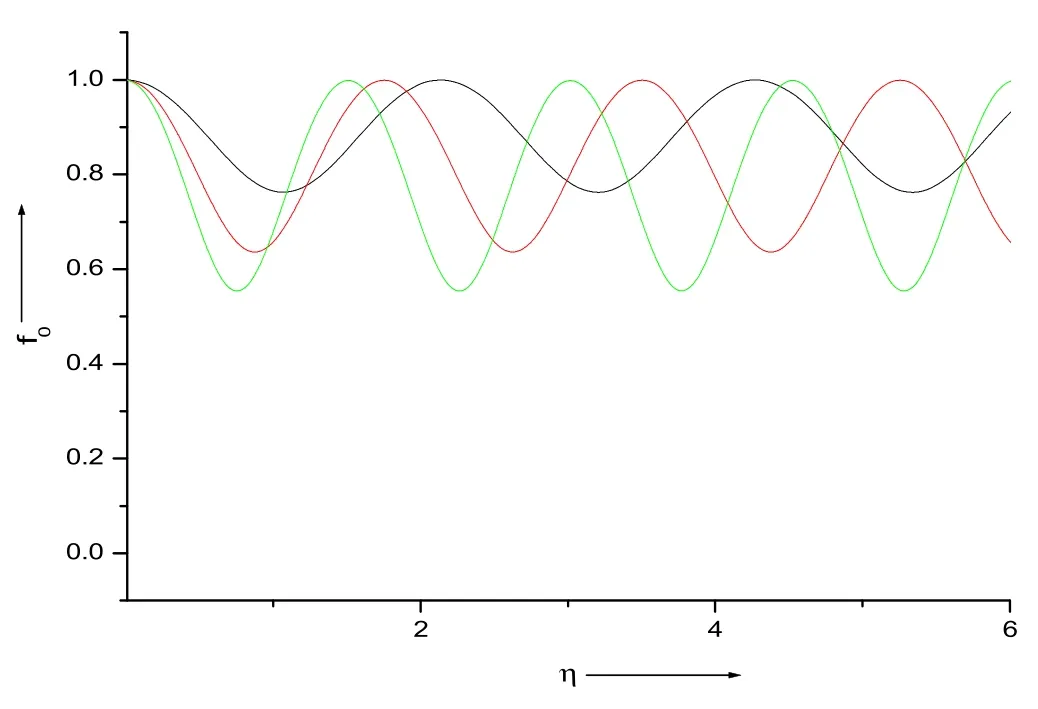
Figure 7.The impact of the pump radius of the beamr0 on the beam width f0 of the pump wave.The black,red and green curves represent r0=20 μm,25 μm,30 μm,respectively.

Figure 8.The impact of the pump radius of the beamr0 on the beam width f of the EPW.The black,red and green curves represent r0=20 μm,25 μm,30 μm,respectively.

The impact of the pump radius of the beamr0on the beam widthsf0,fandfsof the pump wave,EPW and scattered wave is shown in figures 7,8 and 9,respectively.The black,red and green curves representr0=20μm,25μm,30μm,respectively.The beam widths of each beam get shifted towards smallerηvalues with a rise inr0values.The focusing behavior of these waves is increased with a rise inr0values.This is due to the supremacy of the convergence term in comparison to the divergence term at largerr0values.

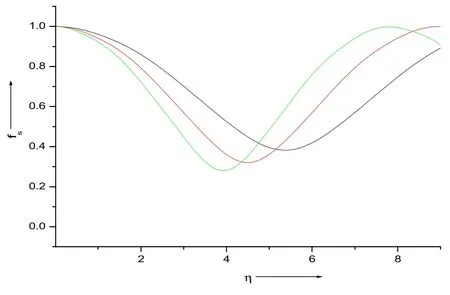
Figure 9.The impact of the pump radius of the beamr0 on the beam width fs of the scattered wave.The black,red and green curves represent r0=20 μm,25 μm,30 μm,respectively.

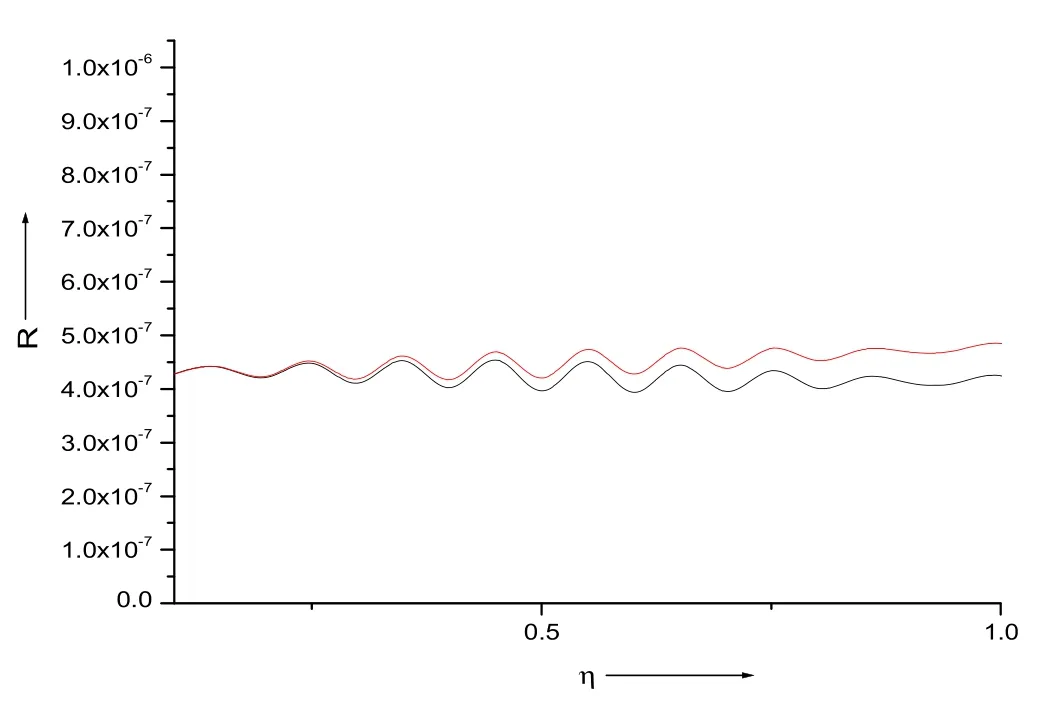
Figure 10.The impact of the intensity of the laser beamon SRS back-reflectivity ‘R’.The intensity parameters=2.0 and 3.0 are for the red curve and black curve,respectively.

The impact of intensity of the laser beamon SRS back-reflectivity ‘R’ is shown in figure 10.The intensity parameters2.0 and 3.0are for the red curve and black curve,respectively.An increment in theparameter causes a reduction in SRS back-reflectivity ‘R’.This is because the extent of the focusing ability of distinct waves involved in the SRS process is reduced at largervalues.The results are in agreement with experimental results [48].

The impact of the density of plasma electronson SRS back-reflectivity ‘R’ is shown in figure 11.The plasma density parameters0.15 and 0.25are for the black curve and red curve,respectively.An increment in theparameter produces an increase in SRS back-reflectivity ‘R’.This is because the extent of the focusing ability of distinct waves involved in the SRS process is increased at largervalues.The results are in agreement with experimental results [49].

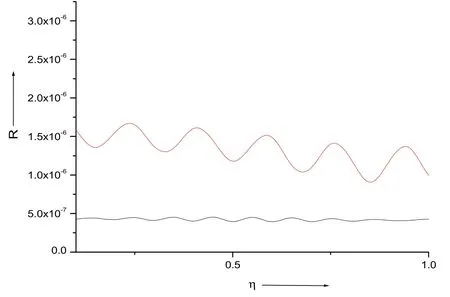
Figure 11.The impact of the density of plasma electronson SRS backrefelctivity‘R’.The plasma density parameters =0.15 and 0.25are for the black curve and red curve,respectively.

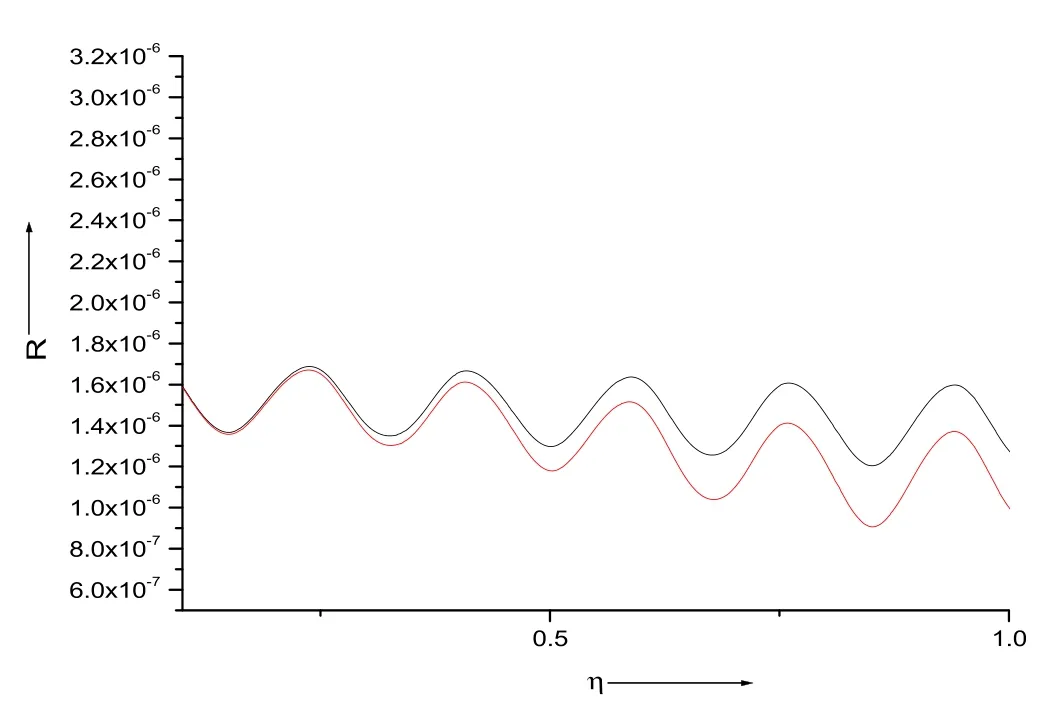
Figure 12.The impact of the pump radius of the beamr0 on SRS back-reflectivity ‘R’.The beam radius parametersr0=20 μ m and 25 μ m are for the red curve and black curve,respectively.

The impact of the pump radius of the beamr0on SRS back-reflectivity ‘R’ is shown in figure 12.The beam radius parametersr0=20μmand 25μm are for the red curve and black curve,respectively.An increment in ther0parameter produces an increase in SRS back-reflectivity ‘R’.This is because the extent of the focusing ability of distinct waves involved in the SRS process is increased at largerr0values.

5.Conclusions

The influence of a self-focused beam on the SRS process in collisional plasma is explored in the present study.The focusing ability of various waves involved in the process is found to get enhanced with a decrease in theparameter and with a rise inandr0values.SRS back-reflectivity is found to get enhanced with a decrease in theparameter and with a rise inandr0values.The results of the present study are really useful in inertial confinement fusion.This is because a decrease in SRS back-reflectivity causes improvement in laser–plasma coupling efficiency.