Disassociation of a one-dimensional cold molecule via quantum scattering

Wen-Liang Li ,Hai-Jing Song ,Tie-Ling Song and D L Zhou

1 Institute of Physics,Beijing National Laboratory for Condensed Matter Physics,Chinese Academy of Sciences,Beijing 100190,China

2 School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3 National Innovation Institute of Defense Technology,AMS,Beijing 100071,China

4 Department of Fundamental Science,Space Engineering University,Beijing 101416,China

Abstract Motivated by the recent experimental developments in ultracold molecules and atoms,we propose a simple theoretical model to address the disassociation,reflection,and transmission probability of a one-dimensional cold molecule via quantum scattering.First,we show the Born approximation results in the weak interaction regime.Then,by employing the Lippmann–Schwinger equation,we give the numerical solution and investigate the disassociation’s dependence on the injection momentum and the interaction strengths.We find that the maximum disassociation rate has a limit when increasing the interaction strengths and injection momentum.We expect that our model can be realized in experiments in the near future.

Keywords: cold molecule,quantum scattering,disassociation rate

1.Introduction

Laser cooling makes atoms or molecules ultracold,e.g.the temperature may arrive at the regime of nano-Kelvin [1–5],which results in the emergence of quantum features of the atoms or molecules,which are usually hidden in the thermal noises from the environments.Thus,the ultracold atoms or molecules become an ideal platform for investigation of fundamental quantum mechanics problems,quantum chemistry,precise quantum metrology,quantum simulations,and even quantum computing [6–13].

Among these applications,ultracold chemistry is closely related to laser-cooled atoms or molecules [14,15].Along this direction,one-dimensional ultracold atoms/molecules,which are formed by a tight confinement with a wave guide[16],play a crucial role due to their relatively simple theoretical model with rich physics [17].

Currently,different kinds of molecules formed from several atoms have been investigated intensively in the literature [18–21].However,the converse process,i.e.the disassociation of molecules into atoms,deserves further studies to deepen its understanding.Here,we propose a simple theoretical model to address the disassociative probability of a one-dimensional cold molecule,and investigate its dependence on the injection momentum and the interaction strengths,which can be arbitrarily tuned via the Feshbach resonance technique[22,23].Our results show that there is a limit of the maximum disassociation rate when increasing both the injection momentum and interaction strengths.

This article is structured as follows: in section 2,we introduce our theoretical model of the scattering problem and give the Hamiltonian.In section 3,we give the eigenstates and the in state of our scattering.Then,we solve the model and show our numerical results by applying Born approximation in section 4 and an integral equation method in section 5.Finally,we present our discussion and conclusions in section 6.

2.The model

We consider a one-dimensional molecule,which is the unique weakly bound state formed by an attractive one-dimensional contact interaction.Then,the one-dimensional molecule scatters with a heavy atom.The Hamiltonian of our system is modeled by

where m1,m2are the masses of the two particles,p1,p2are their momentum operators,and x1,x2are their position operators in one dimension.Here,α,γ1,γ2>0 are interaction strengths of the three contact potentials,where αδ(x2−x1)represents the contact potential between particle 1 and particle 2,γ1δ(x1) represents the contact potential between particle 1 and particle 3,and γ2δ(x2) represents the contact potential between particle 2 and particle 3.Here,we assume that the position of particle 3—a heavy atom—is at zero,and the motion of the heavy atom is neglected.

To solve the scattering problem,we split the Hamiltonian into two parts:

Through this coordinate transformation,we rewrite the Hamiltonian as the representation of the center-of-mass coordinate X and relative coordinate x,where M is the total mass of the two particles and μ is the reduced mass.Then,P is the total momentum and p is the relative momentum.

3.The in state of our scattering

In this section,we will examine the in state of our scattering.Let us start with the eigen problem of H0,which can be divided into two parts:

where

where the eigen wave function is

where |φb〉 is the unique bound state with energyEband the wave function for the bound state

Here,we observe that 〈x|φ(−p)+〉=〈−x|φp+〉,i.e.〈−x|φp+〉is also an eigenstate ofwhich results from the symmetry of space inversion ofi.e.the Hamiltonian is invariant under x→−x.In the Hilbert space of the relative motion,we can show the following complete relation

Now we are ready to give the in state of our scattering

which describes a one-dimensional molecule in the bound state|φb〉scattering on the potential V with the momentum of the mass center P.

4.Born approximation in the molecule channel

In this section,we will apply the Born approximation to our scattering problem.We start with the Lippmann–Schwinger equation:

where the Green function and the free Green function are given by

Therefore,the S matrix in the molecule channel is

The out scattering state in the molecule channel is

Then,the reflection rate and the transmission rate for the molecule are

Therefore,in the Born approximation up to the second order of V:

Note that

Equation (38) implies that Cnbis the disassociation rate,i.e.the rate that the molecule becomes two atoms after the scattering.In addition,only whenis Cnbpositive.

From detailed calculations,we obtain

which can be inserted into equation (39) to numerically calculate the disassociation rate Cnb.

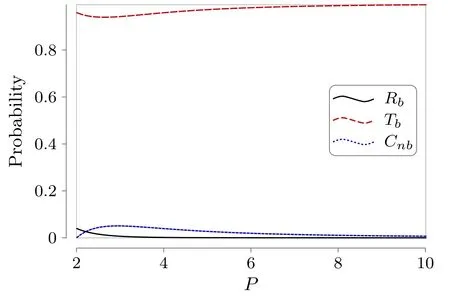
Figure 1.Disassociation under the Born approximation.Here,the parameters are given by m1=m2=1.0,γ1=γ2=0.2,and α=2.0.

Now we are ready to present our numerical results on the transmission rate Tb,the reflection rate Rb,and the disassociation rate Cnbin the first-order Born approximation in figure 1.Here,the parameters are given by m1=m2=1.0,γ1=γ2=0.2,and α=2.0.Due to the energy conservation,only when the mass-center momentum P>2 does the disassociation process occur.With the increase in the momentum P,the transmission rate Tbincreases while the reflection rate Rbdecreases.In particular,the disassociation rate Cnbtake its maximum ≃0.05 at P ≃2.9.

5.Integral equation method

Note that Born approximation is valid only when the momentum P is large,and the interaction strengths γ1and γ2are small.To obtain more general information on the disassociation process,we may resort to the direct numerical solution of the Lippmann–Schwinger equation.

From equations (34),(35),we need to calculatewhich can be obtained from the Lippmann–Schwinger equation (25) and satisfies

Therefore we arrives at the integral equation

and the amplitudes of reflection rate and the transmission rate are given by

5.1.Free Green function

To numerically evaluate the integral equation(43),we need to calculate the free Green function

By detailed calculations (see appendix for more details),the free green function is given by

To further simplify the calculation oflet

Then the second term in the free Green function can be rewritten as

It can be simplified as follows:

Case i: When κ2P2−q2<0,σ=−1,and then

5.2.Numerical results

Now we are ready to perform the numerical solution of the integral equation (43) to obtain |Φ1〉 and |Φ2〉,and calculate the reflection rate Rband the transmission rate Tbvia equations (44) and (45).The basic method of the numerical calculation involves writing the integral equation (43) in a matrix form by discretizing the position variables and taking a suitable cutoff after checking the numerical convergence,and then solving the eigen problem.The disassociation rate can be obtained by Cnb=1 −Rb−Tbin figure 2,where the parameters are given by m1=m2=1.0,γ1=γ2=0.5,and α=2.0.Compared with the case calculated in the Born approximation,we take larger scattering strengths γ1and γ2while keeping the other parameters invariant.As expected,the disassociation channel opens only when the mass-center momentum P>2.With the increase in the momentum P,the transmission rate Tbincreases while the reflection rate Rbdecreases.The disassociation rate Cnbtakes its maximum≃0.1 at P ≃3.2.We also show the Born approximation results in the same parameter setting,which become increasingly accurate with the integral results as P increases,just as one can expect.

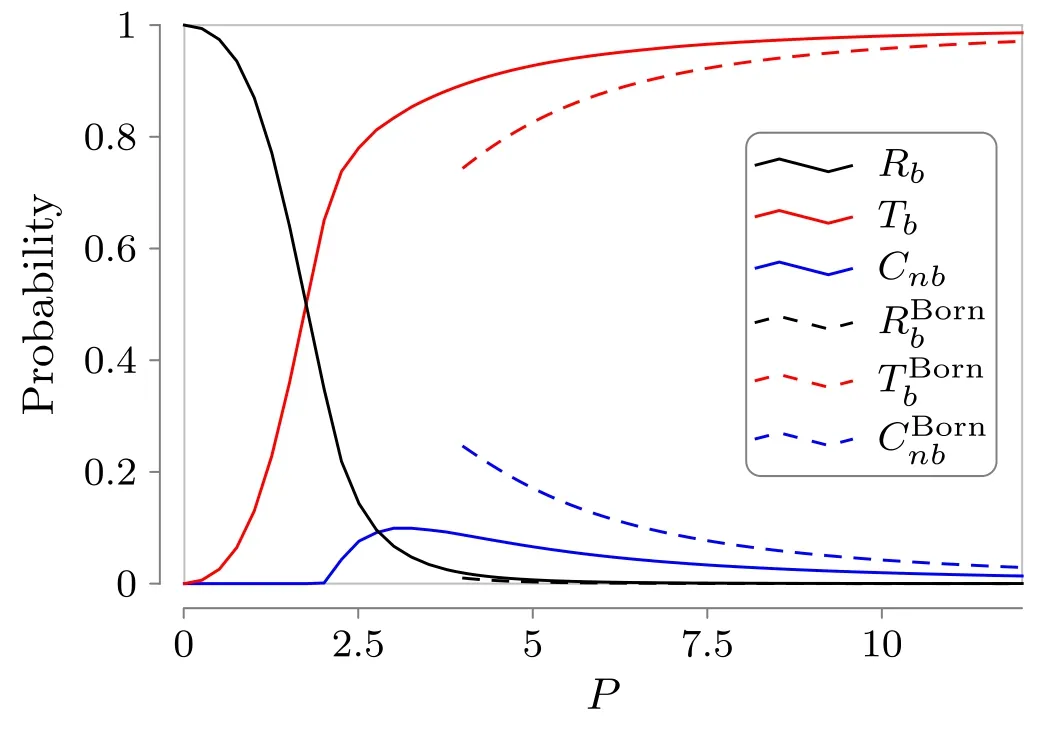
Figure 2.The disassociation rate from numerical solution of the integral equation compared with Born approximation,where the parameters are given by m1=m2=1.0,γ1=γ2=0.5,and α=2.0.

We also care about how the parameters influence the maximum of the disassociation rate.The disassociation rate depends on the mass of each particle,the interaction strengths{γ1,γ2},and the center-of-mass momentum P for a fxied bound strength α.In figure 3,we show that the disassociation rate takes its maximumunder different parameter settings.The solid black lines in figure 3 showwith equal interaction strengths γ1=γ2=γ,and equal mass m1=m2=1.0,while the dashed lines showwith m1=0.5,m2=1.5,and different interaction strengths.The bound strength is α=2.0.Figure 3(a)shows the conditions of P and γ whenwhich means that to reach the maximum disassociation rate,one should increase both P and γ by following the relationships revealed in figure 3(a).This relationship between P and γ comes from the constraint that,for a wave packet which has a typical length,larger incoming momentum P takes more energy to disassociate the molecule but also reduces the interaction time with the potential while,during a long interaction time (which means small P),a larger interaction strength γ would cause the oscillation of the reaction procedure.More precisely,from equations(44) and(45) we can calculate the disassociation rate(A and B are coefficients containing inner products of scattering states and projective states),which approximates to a quadratic function ofand exists as a maximum.Figure 3(b)gives the values ofunder different parameter settings that change with the interaction strength γ,from which we can see that they increase as γ increases and asymptotically reach some limits.For equal mass and equal interaction strengths,the limit ofis 0.5.For γ1=5γ2,the limit is about 0.72,and for γ2=5γ1,the limit is about 0.75.For γ1=0 or γ2=0,the limit approximates to 1.In conclusion,if one wants to reach a higher disassociation rate,one would tune stronger interaction strengths and center-of-mass momentum by following some similar relations given in figure 3(a)and a larger difference between the interaction strengths γ1and γ2.In fact,this maximum valueis irrelevant to the coupling strength α in this situation because this can be reduced to a scaling problem.

Figure 3.The parameters of the solid black lines are m1=m2=1.0,γ1=γ2=γ,and α=2.0.The parameters of the dashed lines are m1=0.5,m2=1.5,and α=2.0.(a) The conditions of center-ofmass momentum P and interaction strengths γ when the disassociation rate Cnb takes its maximum.(b)The maximum of the disassociation rate changing with the interaction strengths γ.

Meanwhile,for different interaction strengths (γ1≠γ2),one would suppose that a larger difference between γ1and γ2would induce a larger disassociation rate.Figure 4 shows more details of the effect,where we keep γ1+γ2=1.0 in figure 4(a)to see the main influence of the difference between γ1and γ2.Figures 3(b)4(b)also show that a lighter particle in the molecule with weaker interaction strength has a higher disassociation rate than that of a lighter particle with stronger interaction strength.

Figure 4.The disassociation rate with different interaction strengths{γ1,γ2 },where the parameters are given by (a) m1=m2=1.0,α=2.0 and (b) m1=0.5,m2=1.5,and α=2.0.

When the coupling of the molecule is strong enough,in the regime of low-injection center-of-mass momentum P the molecule would not disassociate and behave as a single particle.We know the reflection rate Rsingleand transmission rate Tsingleof a single particle scattered by a δ potential,which is a kind of quantum tunneling [24],and in our problem:

Figure 5 shows the reflection and transmission rates of the molecule compared with a single particle for P<10,where the parameters are given by m1=m2=1.0,γ1=γ2=0.5,and α=12.0.

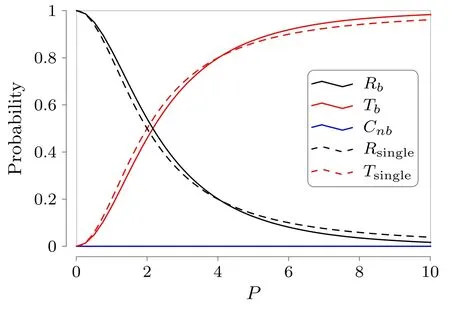
Figure 5.Reflection and transmission rates of the molecule compared with a single particle,where the parameters are given by m1=m2=1.0,γ1=γ2=0.5,and α=12.0.

6.Discussion and conclusion

In this paper,a simple model with contact interactions,which contains the basic process of disassociation of a onedimensional molecule,is proposed to describe the corresponding system of ultracold atoms.The first-order Born approximation is made to obtain the basic physical picture of the process:only when the kinetic energy associated with the injection center-of-mass momentum P is larger than the bound energy can the disassociation process occur.To further validate this picture,we develop the numerical method to solve the integral equation of quantum scattering.With the increases in the interaction strengths and the injection centerof-mass momentum,the maximum disassociation rate will increase.With a larger difference between the interaction strengths,the disassociation rate will increase.And under different parameter settings,the maximum disassociation rate has different limits when increasing the interaction strengths and injection momentum.

In the state-of-the-art experiments of ultracold atoms and molecules [15],ultracold bialkali molecules,such as bosonic23Na39K and23Na87Rb combined by unequal mass atoms,and Na2and K2combined by equal mass atoms,can be produced.Optical confinement can be used to constrain the scattering in one dimension.One can move the molecules using optical tweezers or can relatively introduce a moving heavy atom or scattering potential.While putting all the techniques together is not a straightforward endeavor,we see no major roadblock in implementing such a scattering model.We expect that our model can be realized in the experiments of ultracold atoms and molecules in the near future.

Acknowledgments

We thank Peng Zhang for the useful discussions.This work is supported by the National Key Research and Development Program of China (Grant No.2021YFA0718302 and No.2021YFA1402104),the National Natural Science Foundation of China (Grant No.12 075 310),and the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB28000000).

Appendix

In this appendix,we show the details of the derivation of equations (59) and (60) giving the free Green function.

The first term of the Green function

When x>0,y>0,the above equation becomes

ORCID iDs