用于食品冷冻温度控制的模糊控制系统设计

刘向勇 高雪飞 董 强 李 琼

(1. 中山市技师学院,广东 中山 528400;2. 广东工业大学,广东 广州 510006;3. 华南农业大学,广东 广州 510642)

食品加工作为一个关键的生产环节,对食品质量的保障和生产效率的提升具有重要意义[1-2]。在这个背景下,就使用低温冷冻隧道的食品加工厂而言,对食品传送带滚子转速的控制以及冷冻隧道温度提出有效的控制策略显得尤为关键[3]。周舟等[4]研究了冷冻温度和冷冻中心温度对面条冷冻面团与最终面条品质的影响,从而确定最佳的冷冻温度和冷冻中心温度。Bao等[5]综述了影响肌肉类食品冷冻和冷冻贮藏的主要理化因素。Wang等[6]开发了一种综合建模方法来估计加工厂制冷温度升高对能源消耗、产品温度和食品微生物的影响。Svendsen等[7]综述了冷冻加工生产线中可采用的工业方法和技术。

国际上,比例—积分—微分(proportional-integral-differentiation,PID)控制器作为一种经典的控制方法,被广泛应用于工业自动化中[8]。有学者[9]尝试使用PID控制器来实现对食品传送带滚子转速的控制,但在面对非线性和时变特性时,其控制性能受到限制,在实际应用中,仅使用传统PID控制策略可能难以满足食品加工过程中对精确控制的要求[10]。

针对冷冻隧道温度调节,传统的比例—积分(proportional-integral,PI)控制器被广泛应用于工业领域,但在一些具有时滞和非线性特性的系统中,其控制性能受到挑战[11]。研究[12]表明,单一的PI控制策略可能难以应对温度变化较快或系统动态性较强的情况。吴光辉[13]分析了冷冻调理食品的主要特性和质量控制方法,重点介绍了几项冷冻调理食品的质量控制方法的具体应用。王安敏等[14]设计出一种通过BP神经网络调节PID算法参数的温度控制系统,该系统通过脉冲宽度调制技术控制压缩机冷冻以达到精确控制温度的目的。

尽管已有研究提出了针对食品传送带滚子转速和冷冻隧道温度的一些控制策略,然而在实际应用中仍然面临控制器参数调整困难、非线性和时变性方程难以处理、系统鲁棒性不足、设定点调整困难等问题[15]。例如,由于变量与食品系统的非线性之间的强耦合,通过使用低温冷冻设备对食品温度的控制变得复杂。目前,大多数使用低温冷冻隧道的食品加工厂通过手动调节冷冻隧道的速度和温度控制回路的设定值来进行控制,导致工艺输出出现偏差,这主要源于操作人员之间的控制标准以及后者对工艺条件变化的反应速度不同造成的[16]。

为解决现有研究中存在的以上问题,通过引入PID、PI以及Takagi-Sugeno模糊控制算法,设计用于食品冷冻温度控制的模糊控制系统,该控制系统包括用于食品传送带滚子转速的PID控制器、用于冷冻隧道温度调节的PI控制器,并采用Takagi-Sugeno模糊控制器来设定温度调节PI控制器的温度设定点。该系统采用经典控制和模糊逻辑技术相结合的控制策略,将连续进料隧道内使用液氮喷射低温喷雾冷冻设备的食品(例如金枪鱼肉排)冷冻过程的流量和温度控制回路结合起来。

1 理论基础

1.1 深冻

在深冻(食物的热中心温度达到-18 ℃)过程中,食品中所含水分从液态转化为固态,从而使食品的特性发生重大变化[17]。这些特性包括密度、热导率、热焓、热扩散率、潜热和比热;而这些特性又取决于食品成分、含水量、温度和食品本身的成分等因素[18]。水、蛋白质、脂类、碳水化合物、灰分和纤维是对食品热特性影响最大的成分,因为它们的变化和特性与温度密切相关。食品中某些化合物的物理特性随温度T变化的计算方式如表1所示[19]。

表1 食品中某些化合物的物理特性随温度T变化的计算方式

当前,由于低温隧道中使用的液氮冷冻系统具有强大的制冷能力,食品的深冷过程相对简单,常用液氮冷冻系统如图1所示,主由两部分组成:① 将食品置于-20～-90 ℃温度范围内的冷冻隧道;② 负责将食品从隧道式冷冻机的入口输送到隧道式冷冻机末端的变速传送带。

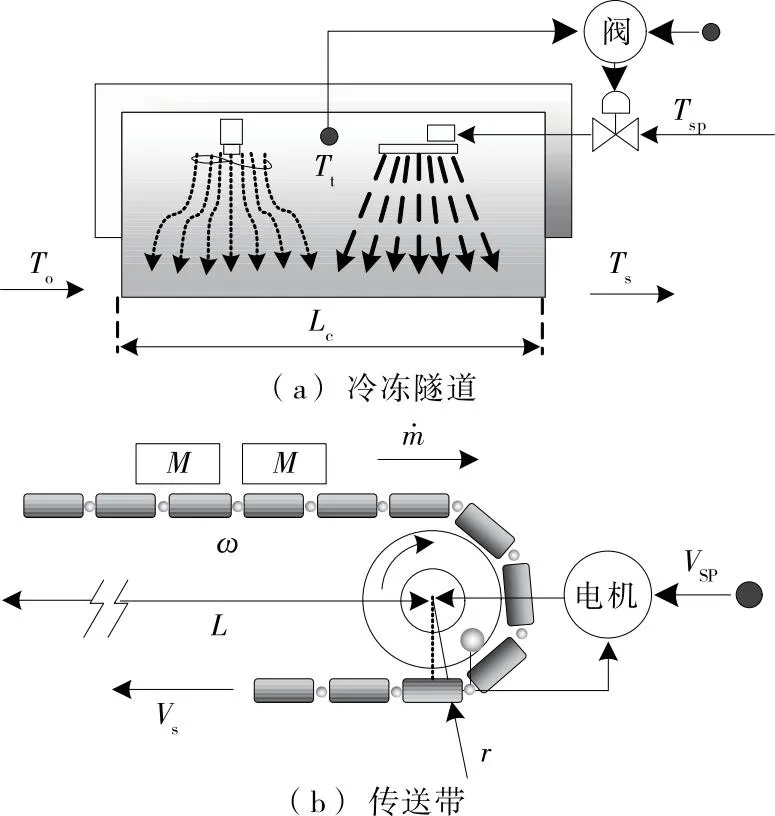
To. 初始食品温度(℃) Tt. 冷冻隧道温度(℃) Ts. 出口食品温度(℃) Lc. 冷冻隧道长度(m) Tsp. 设定点温度(℃) M. 食品质量(kg) m. 食品质量流量(kg/s) Vs. 食品输出速度(m/s) VSP. 速度的设定值(m/s) ω. 传送带电机的角速度(rad/s) r. 传送带的牵引圆柱半径(m) L. 传送带传送距离(m)

为提升冷冻过程的经济性,需要一种良好的控制机制,在保持食品所需的性能的同时,尽量减少过冷或欠冷造成的损失。

1.2 冻结阶段

液氮冷冻的主要优点是食品在冷却设备中所需的时间缩短。为了控制这种冷冻过程,有必要确定食品热中心温度达到-18 ℃所需的时间。实践中,使用了一些假设来获得冷冻过程的简化模型,冷冻过程分为3个阶段:预冷、冻结和回火或过冷阶段,如图2所示[20]。

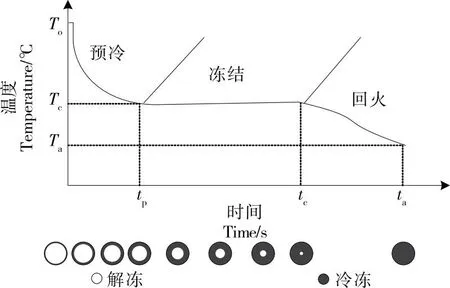
To. 食品初始温度 Tc. 食品冻结温度 Ta. 食品回火温度 tp. 食品预冷段稳定时间 tc. 食品冻结段稳定时间 ta. 食品回火或过冷段稳定时间

食品的冻结时间tc可由式(1)给出[21]。

(1)

式中:

Tt——冷冻隧道在时刻t的温度,℃;

To——冷冻隧道的初始温度,℃;

ρ——食品冻结后的密度,kg/m3;

λ——结晶潜热,kJ/kg;

P、R——取决于食品的尺寸和形状的常数;

d——食物的厚度,m;

hs——热量传递对流系数,W/cm2。

1.3 系统识别

为建立所提出的模糊控制器模型,首先确定控制过程的测量变量,即输入(控制变量)、输出(受控变量)和可能的干扰。为获取控制过程的动态信息,激发控制过程并记录其输入和输出。为分析控制结果,采用一些试验识别技术,例如基于对阶跃响应过程反应的曲线或自回归模型[22],此类方法属于开环方法,可以安装也可以不安装控制器(在后一种情况下,控制器将在测试期间“手动”运行);根据系统响应,可以获得表示模型控制过程的参数。ARX型自回归模型(auto regressive with eXogenous input)是一种线性离散模型,其在采样时间“n”处的输出是从先前的输出值和输入值(n-1、n-2等)中得到的。此外,还可加入白噪声[23]。通过对拟合参数进行多元线性回归计算,使实际值与模型估计值之间的二次方差值最小。

研究选用ARX型自回归模型,因为该模型除了相对简单外,还能很好地拟合在对所研究的工艺流程进行阶跃输入时记录的输入—输出数据。

1.4 控制器设计

控制器的设计基于执行特定流程任务所需的一系列要求。这些要求代表了系统的性能指标,包括准确性、相对稳定性和响应速度。要想获得令人满意的系统性能,首先要进行一次开环比例增益调整。然而,在大多数实际情况下,仅靠这种调整并不能充分改变系统的行为,使其有可能符合所给的规范,因此有必要修改系统的动态行为。

极限增益法可被用于将控制器曲线调整为闭环系统响应曲线,并考虑以一定的速率抑制“A”增益,如图3(a)所示[24]。该方法包括确定比例式控制器的增益,该控制器可产生持续振荡响应,即振幅恒定的振荡,如图3(b)所示;所述信号的周期为“Pu”。

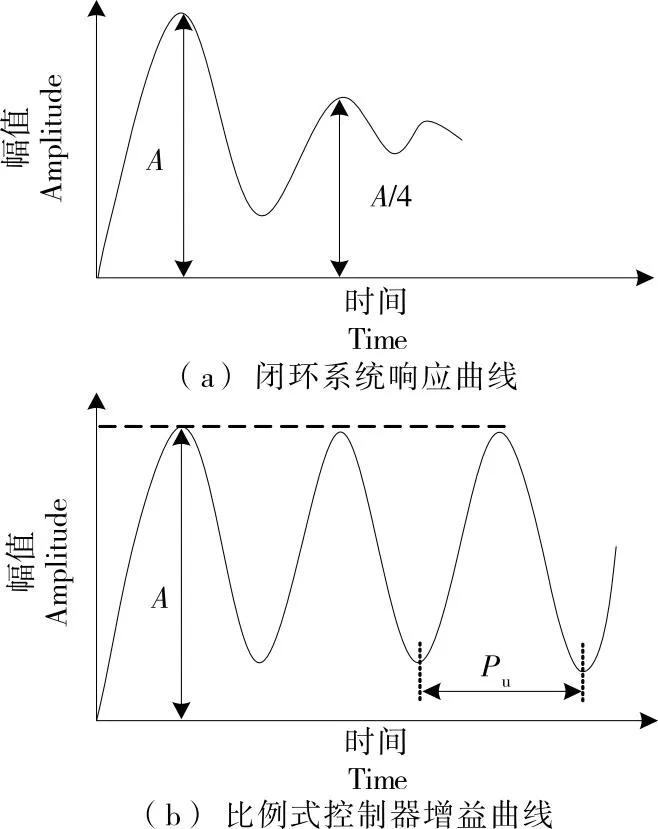
图3 闭环系统响应曲线和比例式控制器增益曲线

1.5 模糊控制器

基于模糊逻辑的模型的基本原理是一套启发式规则,其输入和输出变量都是语言变量,由模糊集表示[25]。模糊控制器一般由图4所示的4个操作模块组成,“u”和“y”分别为输入和输出。

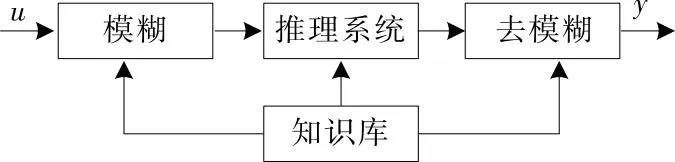
图4 模糊控制器的一般结构

模糊化使用隶属函数将物理系统输入变量转换为模糊变量。在此,定义了输入变量的变化范围,以及与之相关的模糊集及其各自的隶属函数。在去模糊化过程中,从推理系统中获得的模糊变量被转换为实际输出变量。为此,通常采用以下数学方法之一:最大值法、中心点或区域中心法和加权模糊平均法[26]。知识库或数据库定义了控制和处理有关模糊集隶属度函数的模糊信息的语言规则。

最后,推理系统依靠控制器规则和模糊推理来计算与实际输出变量相关的模糊输出。

Mamdani和Takagi-Sugeno是两种最常用的模糊控制器,它们的特点取决于模糊输出的定义方式。Mamdani模糊控制模糊规则的一般形式如下:

如果u1是Ai、u2是Bi,那么y是Ci。

这种控制器的输出是一个模糊集,因此需要一个去模糊化步骤来获得控制器输出的离散值。

Takagi-Sugeno型模糊控制的模糊规则形式如下:

如果u1是Ai、u2是Bi,那么y=f(u1,u2)。

Takagi-Sugeno型模糊控制器的输出不需要模糊化阶段,可以直接获得离散值。

2 食品深冷过程的模糊控制系统设计

2.1 系统识别

2.1.1 速度控制 深冷冷冻设备输送带速度控制系统采用基于PID的控制,负责调节输送带牵引辊的转速。

使用LabView软件中的系统识别工具来获取设备的自回归模型,并将每个模型的响应与从系统中提取的真实数据进行比较。一阶加“死区”时间模型的响应与实际响应有很大偏差,而二阶模型虽然偏差较小,但其响应也与系统的实际行为不同。而在LabView SITK(系统识别工具包)工具的帮助下确定的ARX模型是最能体现输送带牵引速度过程的模型,其传递函数定义为

GC(S)=(0.167S4-2.32×10-32S3+8.90S2-1.24×10-31S+42.73)/(S5+10.37S4+76.30S3+233.68S2+129.49S+31.02)。

(2)

确定了模型,便可确定速度控制的调整参数。为此,采用齐格勒和尼科尔斯极限增益法,获得PID控制函数H1(s)的调节参数。其响应平稳时间为29.5 s,超过峰值的幅度小于峰值的25%。

2.1.2 温度控制 如图1所示,低温冷冻设备温度控制的运行原理是,根据PI控制器的设定值,通过打开液氮流量阀来调节冷冻通道的温度。

为了正确调整这一控制,采用与速度控制相同的程序,从而建立了对冷冻隧道温度进行控制的模型,其定义为

GP(S)=(0.016S4-3.30×10-34S3+0.002S2-4.39×10-36S+2.54×10-5)/(S5+0.70S4+0.18S3+0.02S2+0.001S+1.94×10-5)。

(3)

采用极限增益法对温控的调整参数进行了估计。针对PI型控制器[传递函数为H3(s)]调整的参数,确保了375.0 s的稳定时间和小于20%的超峰响应。

2.1.3 冻结过程的建模 为确定食品的最终温度(Ts或TF)值,建立以暴露或冷冻时间(tc)、冷冻隧道温度(TT)和食品初始温度(To或Ti)的函数表示的冻结过程模型,以式(1)为基础,并考虑以下假设:

(1) 结晶潜热(λ),也称为焓变(ΔH),将作为最终温度下进料焓[HF=h(TF)]与进料初始焓[HI=h(Ti)]之差的函数来确定,即

ΔH=HF-HI=h(TF)-h(Ti)。

(4)

(2) 通过低温冷冻隧道长度(Lc或LT),冷冻隧道温度应被视为均匀且等于TT。

(3) 变量是食物的密度值(ρ)和导热系数(Kc),ρ和Kc的计算公式如表1所示,二者的值均与温度有关。

(4) 在冷暴露时间(tc)内,食品的厚度(d)保持不变。

根据上述假设,食物最终达到的温度将根据无穷大平板的冷冻过程计算得出,其计算公式如式(1)所示,最终进料焓值按式(5)计算。

(5)

式(5)中,tc可以由传送带的驱动辊速度(ω)、辊的半径(r)和冻结隧道的长度(LT)之间的关系确定,即:

(6)

比较式(1)和式(5),并假定食物装在暴露在空气中的两块板之间,即“P”等于1/2和“R”等于1/8,可以得出K与厚度“d”、表面系数(hs)和导热系数(Kc)的关系如下:

(7)

在对食品冷冻过程进行建模后,用温度记录仪采集的真实数据对模型进行了验证(见图5)。

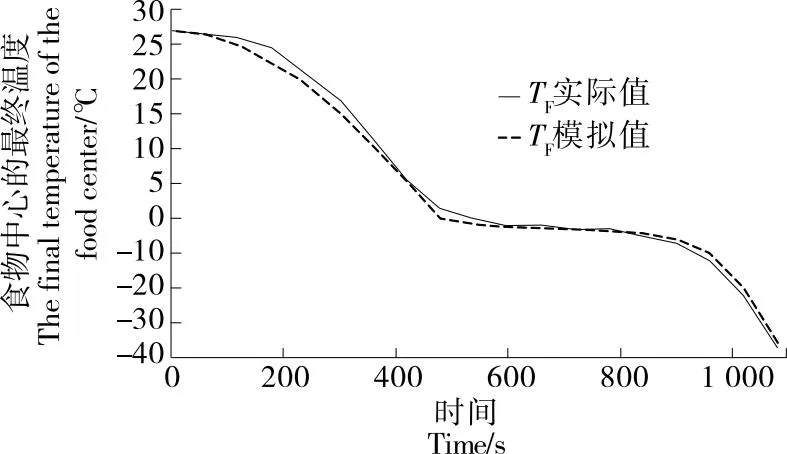
图5 真实TF温度与模拟TF温度的比较

鉴于图5中显示的两个响应之间的相似性,可以认为所开发的模型是有效的。

2.2 系统方案

2.2.1 质量流量控制 在食品深度冷冻过程中,设备操作员在控制面板上设置设定点值,根据所需的食品流量来调节传送带的速度。因为食品是人工喂入的,显然不可能对食品的质量流量进行正确的控制,从而导致生产线生产率的损失,以及设备制冷能力的浪费。为了解决该问题,可通过连续称重系统来调整控制回路,以获得输送带速度与放置在其上的质量之间的关系,从而确定过程的最大流量,如图6所示,其中H2(s)为PI控制器的传递函数。

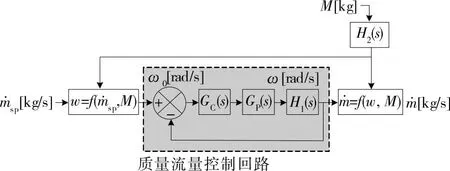
图6 所提质量流量控制回路

2.2.2 冷冻温度控制 在待优化的系统中,控制是根据待加工食品、传送带速度(ω)和隧道入口处的进料温度(TI)手动调节隧道温度设定值来实现的。

在此控制过程中,设定点由操作员根据以下标准设定:

(1) 工作温度应尽可能高,以避免氮气消耗过多。

(2) 温度控制器起PI调节器的作用。

(3) 传送值的调整旨在确保食品在冷冻隧道出口处至少达到-18 ℃。

值得注意的是,隧道出口处的温度审查是由设备操作员进行的,设备操作员在发现设备不符合规范时,会根据上述前提调整隧道控制回路的输出值。这导致决策(改变设定点)的延迟,从而在进料冻结过程开始时出现偏差。为了克服这些不足,提出了一种控制策略,其操作重点是估算冷冻隧道(TT)的设定温度,以便根据待加工食品的类型、初始温度(TI)和传送带辊筒(ω)的速度,使最终温度达到-18 ℃或更低。为此,上述变量(TI、ω和TT)将作为关键信息,以便通过模糊控制逻辑,为隧道温度控制获得设定值,从而实现比操作员控制更佳的控制性能。为此,需要对现有设备进行一些修改,以提升以自动方式控制冻结过程的可能性,如图7所示,其中GV(s)表示式(5)对应的传递函数。

图7 所提温度控制回路

2.3 模糊控制器设计

控制器的设计过程主要根据要冷冻的食品、食品的初始温度值和食品在低温隧道内的暴露时间来确定隧道温度值,以便在冷冻过程结束时获得预定的出口温度。因此,进料的初始温度(Ti)和传送带驱动辊的速度(ω)被设定为输入变量,而输出变量将定义低温冷冻隧道温度控制回路(TT)的设定值。

对于输入变量,为每个变量定义了模糊集(Ti为6个,ω为11个);而对于输出变量(TT),定义了5个模糊集。在定义模糊集时,使用了式(5)给出的食品冷冻模型,以确定TF约为18 ℃时所需的TT值,该值是温度对(ω,Ti)的函数。针对金枪鱼排的具体情况总结见表2。

表2 TT值与ω和Ti的函数关系(金枪鱼排)

针对研究所考虑的情况,定义了一套基于Mamdani型模糊控制器的规则。根据表2中的数据,制定了一个推理规则矩阵,如表3所示。

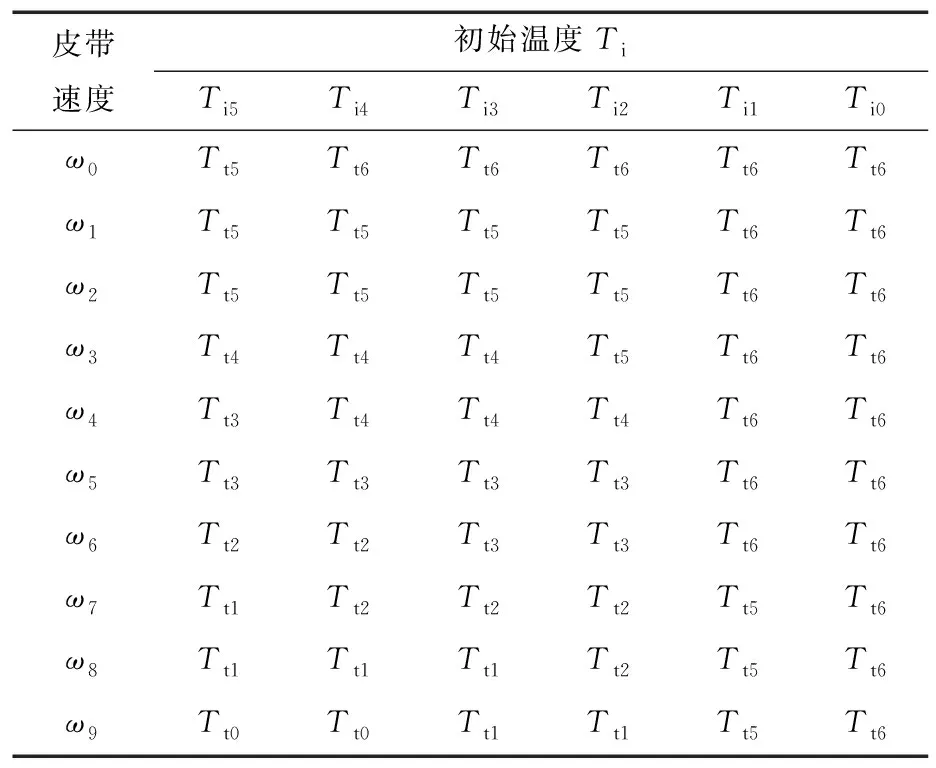
表3 TT的推理规则

作为模糊控制器开发的最后一部分,选择了使用中心点法进行去模糊处理,这主要是考虑到该方法在实施过程中的实用性和高效率。为了验证控制器输出响应的准确性,根据Ti和ω值的组合,以相对误差的形式确定了控制器输出响应与表2所示值之间的差值,见表4。

表4 Mamdani (TT)的控制偏差

研究结果表明,如果采用Mamdani型控制器将产生额外的液氮消耗量,这主要是由于待处理食品的过冷造成的,即有必要通过修改模糊集来重新设计控制器。

重新设计模糊控制器:根据初始温度值Ti隧道温度值与ω的函数关系,定义方程组(8),该方程组确定了在食品初始温度(Ti)的特定值下,隧道温度(TT)与传送带辊筒速度(ω)的关系,即给出了所有可能初始温度条件下TT的可能取值。

(8)

式(8)中描述的方程组将作为开发Takagi-Sugeno型控制器模糊规则的基础,即

如果Ti1>Ti≥Ti2,则TT为f(TT(Ti);ω)。

其中,f(TT(Ti);ω)是对Ti所属范围[Ti2,Ti1)内TT的极值进行内插值的结果。

与使用Mamdani控制器一样,对于TI和ω的每个值,都可获得隧道温度的控制器输出值,其与实际值的偏差见表5。从表5可看出,在最坏情况下,单个值的百分比偏差不超过3%,而Mamdani控制器在大多数情况下偏差超过5%,因此,Takagi-Sugeno型控制器的系统响应效果更好。

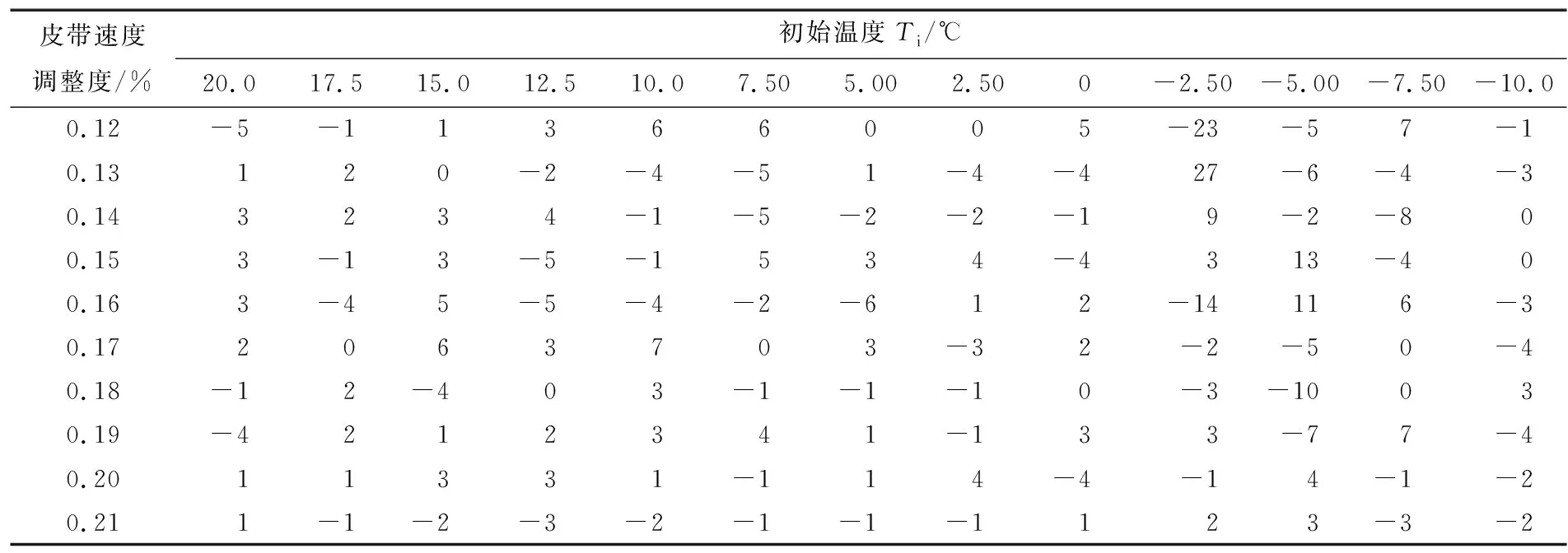
表5 Takagi-Sugeno (TT)的控制偏差

3 对所提系统的有效性评估

为对所提系统进行有效性评估,首先搭建所提系统的整体控制回路。具体步骤包括:① 获得皮带速度回路控制器和隧道温度控制器的调整参数;② 确定了质量流量控制回路配置和模糊温度控制回路设计方案;③ 获得整体控制系统回路,如图8所示。

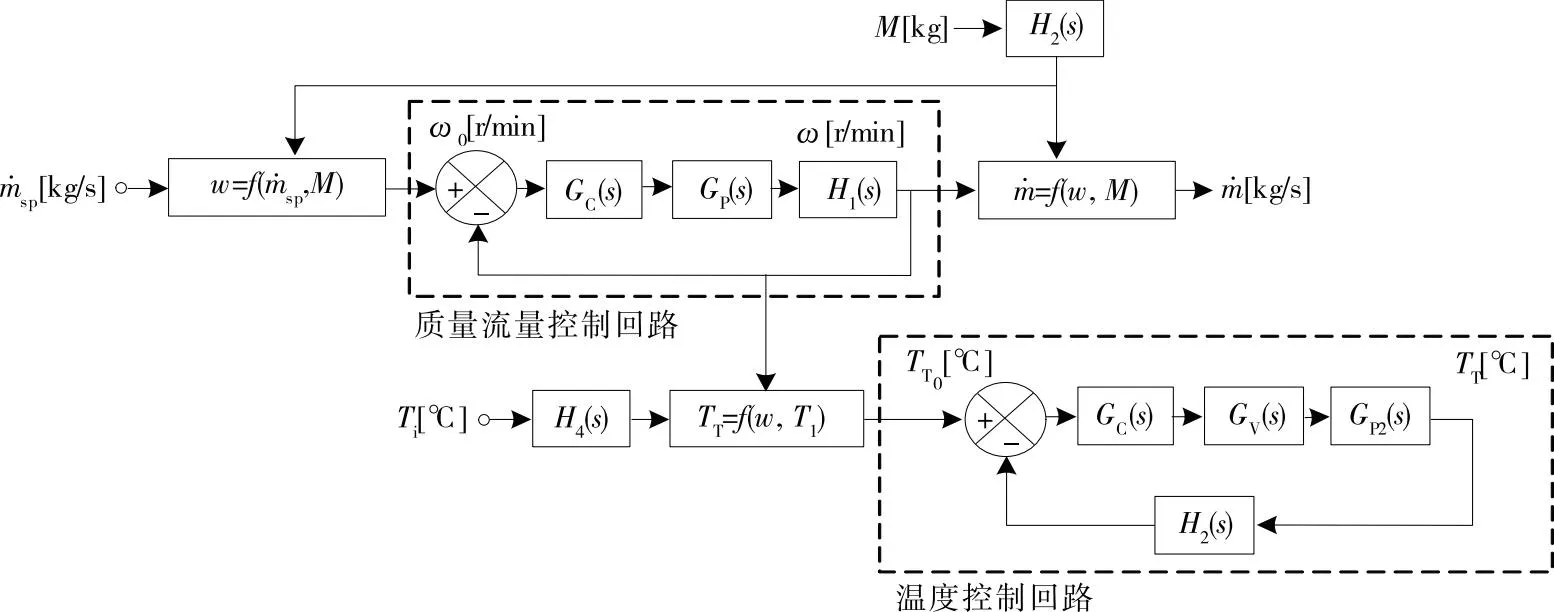
图8 控制系统的完整框图

在LabView环境中进行仿真配置后,对所提系统进行了一系列测试,例如,改变运行条件和施加干扰,以对系统性能进行评价。

3.1 对质量流量控制器设定点变化的响应

该试验考虑了以下初始条件:试验材料金枪鱼肉排;初始温度10 ℃,总质量200 kg;仿真时间1 000 s。

如图9所示,待冷冻食品的质量流量从650 kg/h增加到700 kg/h,驱动辊的转速从1.62 r/min增加到1.75 r/min,这反过来又导致模糊控制器将隧道温度降低到-60 ℃,从而使最终食品温度(TF)达到约-18 ℃。

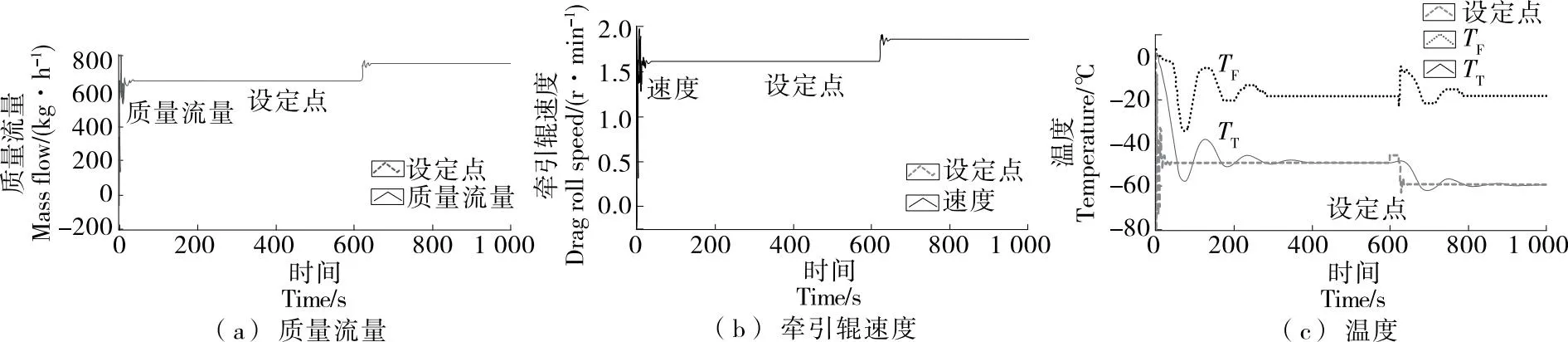
图9 系统对设定值变化的响应

3.2 对总质量扰动的响应

保持与第1次试验相同的初始条件,并在仿真时间达到600 s后施加20 kg的正阶跃变化(金枪鱼的质量从200 kg增加到220 kg),得到图10所示的结果。仿真结果表明,待冷冻食品质量的变化会直接影响控制传送带驱动辊速度的环路的行为(转速从1.62 r/min降至1.47 r/min),进而延长食品在冷冻隧道内的暴露时间。在这种情况下,模糊控制器会做出反应,修改隧道温度设定点,对干扰进行了有效补偿。

图10 系统对总质量扰动的响应

3.3 对初始温度扰动的响应

试验中,初始条件与第1次试验相同,并在仿真时间达到600 s后,对金枪鱼肉排的初始温度进行+5 ℃的阶跃变化。第3次测试的结果如图11所示。

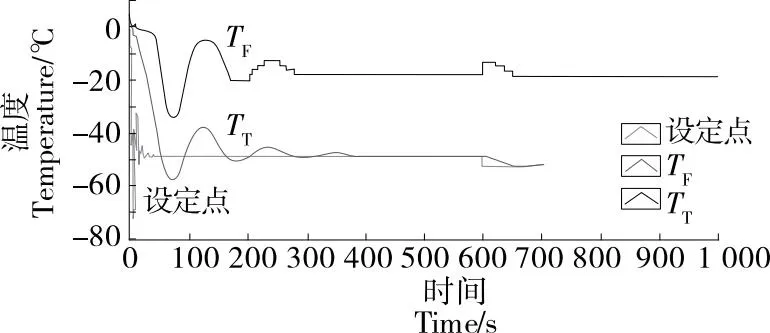
图11 所提系统对初始温度扰动的响应

此时,食品入口温度的任何干扰都会导致模糊控制器动作,以便快速有效地将食品的出口温度保持在预期值(即-18 ℃)附近。

3.4 应用效果分析

将所提控制系统应用于液氮冷冻系统,测试过程仍考虑以下初始条件:试验材料金枪鱼肉排;初始温度10 ℃,总质量200 kg;运行时间1 000 s。应用结果:

(1) 待冷冻食品的质量流量从650 kg/h增加到700 kg/h,驱动辊的转速从1.62 r/min增加到1.76 r/min,这反过来又导致模糊控制器将隧道温度降低到-60.5 ℃,从而使最终食品温度(TF)达到约-18 ℃。

(2) 在运行时间达到600 s后施加20 kg的正阶跃变化(金枪鱼的质量从200 kg增加到220 kg),待冷冻食品质量的变化会直接影响控制传送带驱动辊速度的环路的行为(转速从1.62 r/min降至1.45 r/min)。

(3) 在运行时间达到600 s后,对金枪鱼肉排的初始温度进行+5 ℃的阶跃变化,所提控制系统可快速有效地将食品的出口温度保持在预期值(即-18 ℃)附近。

以上分析结果表明,所提系统在实际液氮冷冻系统上的应用效果与仿真效果非常相似,这进一步证明了所提系统的有效性。

4 结论

设计了用于食品冷冻温度控制的模糊控制系统。对所提系统进行了一系列测试,对测试结果的分析表明:输出变量的值不会在设定值附近出现大幅波动,该效果可通过选择允许快速响应和相对较低超调的系统参数来实现;使用Takagi-Sugeno原理开发的控制器的响应与预期值的偏差较小,且易于实施;当所述系统受到不同的扰动时,所提出的控制系统能够进行快速且稳定的响应;操作人员积极参与手动调整输送带速度和冷冻隧道温度的设定值时,使用模糊控制器明显具有优势。但研究未分析所设计系统参数调整的一般规律,后续将对其进行深入讨论。