基于改进Canny算法的噪声图像边缘检测

孙海明，韩国强

（1.湖北汽车工业学院 机械工程学院，湖北 十堰 442002；2.湖北中程科技产业技术研究院有限公司，湖北 十堰 442002）

图像边缘与椒盐噪声都具有高频跳跃的性 质［1］，对噪声图像进行边缘检测时易引起边缘线误检的情况，影响后续图像处理［2］。Canny 算法［3］因其3个特性成为图像边缘检测常用算法，但对图像求解过程中会遇到椒盐噪声干扰，确定边缘高低阈值存在一定难度［4］。徐武［5］等在滤波设计上进行改进，有效滤除了椒盐噪声并保护图像边缘细节信息；付文博［6］等结合CNN与Canny，设计出C-Canny算法，提高了阈值定位的准确率；刘元峰［7］等侧重研究目标区域，然后基于改进的Canny算子进行噪声消除，提高了目标检测的准确率；李静［8］等使用自适应中值高斯滤波设计代替经典Canny 算法中的高斯滤波器；李靖［9］等使用多尺度细节法增强边缘，降低了高斯滤波的影响。上述改进算法具有降噪处理的步骤，但处理方法的鲁棒性不高，降噪后容易导致图像边缘模糊，造成图像弱边缘漏检。针对经典Canny 算法及其相关研究在实际应用中遇到的问题，提出使用自适应中值-高斯滤波法（AMGF）代替高斯滤波法滤除图像噪声，并通过拉氏（Laplace）变换增强去噪后的图像；使用Otsu 法计算得到图像最优阈值,运用精度更高的Scharr 算子代替Sobel 算子计算图像梯度，以此提高边缘点定位精度以保证后续边缘连接的准确性。

1 改进Canny算法

经典Canny算法存在以下缺点：1）采用高斯滤波进行图像去噪，利用二维高斯函数的分布方式平滑图像，可以抑制服从正态分布的噪声，但对椒盐噪声很敏感，且滤波模板大小的选取受人为影响，卷积核半径小会导致噪声去除效果差，卷积核半径大会使图像变得模糊，丢失图像信息；2）采用Sobel卷积核进行梯度大小的计算，提取到的边缘信息精度较差；3）根据人为经验选取高低阈值，不依靠图像自身特性来进行最优阈值的判定，无法得到图像的确定信息，造成检测误差。针对上述缺陷进行改进：使用自适应中值-高斯滤波并融合Laplace 变换，设计AMGF-L 方案；使用精度更高的Scharr 算子代替Sobel 算子进行图像梯度计算；运用最大类间方差法（Otsu算法）自适应选择图像的最优阈值。改进边缘检测算法流程如图1所示。

图1 改进算法边缘检测流程图

1.1 AMGF-L方案

传统中值滤波对图像中少量椒盐噪声起到的作用较好，但当图像噪声密度增大时很难在有效减少噪声的同时保留图像细节信息。自适应中值滤波针对特定图像条件，动态地改变中值滤波器的窗口宽度，保证去除噪声同时保留图像细节特征。算法步骤如下：1）设Sxy为滤波器的作用区域，滤波器窗口所覆盖的区域中心点为图像中第x行第y列个像素点；Sxy中最小灰度值、最大灰度值、中间灰度值分别为Zmin、Zmax、Zmed；Zxy表示图像中第x行第y列像素点的灰度值；Sxy所允许的最大窗口尺寸为Smax。2）当(Zmed-Zmin)大于0 且(Zmed-Zmax)小于0时转至步骤3），否则增大窗口的尺寸，如果增大后的尺寸不大于Smax，则重新执行步骤2），否则直接输出Zmed。3）当(Zxy-Zmin)大于0且(Zxy-Zmax)小于0时输出Zxy，否则输出Zmed［11］。

经过自适应中值滤波处理，椒盐噪声得到了有效控制，接着运用自适应高斯滤波法去除高斯噪声。利用二维高斯滤波函数生成高斯核：

式中：k为高斯核半径；σ为标准差。高斯核系数权值与方差具有特定比例关系［12］，在卷积窗口滑动中，根据方差大小求得高斯核标准差σ。图像某区域内方差计算公式为

式中：Si,j为中心点(i,j)的卷积窗口；D(i,j)为方差，D(i,j)越大，表示像素值在Si,j区域内的离散程度越高，因此采用更小的σ生成的高斯核系数权重，可以有效减少对该区域的影响。据此得到：

由于D(i,j)是常量，R(i,j)是关于k与σ的函数，即

当R为1时，高斯核中参数权重大小与像素值权重最接近，此时该处σ由Sxy区域内像素值的方差D求得。以此类推，反复迭代，形成自适应高斯滤波，最后对图像像素点全部卷积完成高斯滤波处理。

图像经滤波处理后造成图像清晰度变低，边缘信息不易体现，使用Laplace 算子对图像进行锐化处理，相比一阶微分算子定位张力相对较强，锐化效果更佳。将锐化后的图像与原图像融合在一起，保留原图信息并增强图像梯度突变处的像素值，实现图像边缘的增强。常用Laplace算子模板为

Laplace算子的二阶导数用来描述二维图像的同性函数，表示图像的特征和性质：

边缘增强公式为

式中：g为输出；f为原始图像；c为细节系数。根据c值大小判断像素点是否被增强。

1.2 计算梯度强度和方向

经典Canny 算法采用Sobel算子进行图像梯度定位，精度较差，容易丢失边缘信息［13］。Sobel算子由2组3×3矩阵组成：

在X和Y方向上计算出梯度强度：

式中：Gx为像素点水平方向的梯矢量；Z为图像；Gy为像素点垂直方向的梯矢量。计算图像每个像素点的梯度大小G和梯度方向θ：

选取OpenCV库中的Scharr算子［14］代替Sobel算子，以提高精度且同时保证运算效率。Scharr 算子滤波模板替换为

1.3 Otsu确认阈值

Otsu算法是自适应的阈值选择技术，能够根据灰度特性将图片分为背景和前景［15］。为定义阈值T，将图片中的像素点分为2类，即元素值不大于T（背景区域）和元素值大于T（前景区域）。假定背景区域占总像素数的比例为ω1，即

式中：Ssum为所有像素点总和；N1为背景区域所有像素点数。前景区域占总像素数的比例为

式中：N2为前景区域所有像素点数。依靠方差概念，类间方差g为

式中：μ1为背景区域平均像素值；μ2为前景区域平均像素值。优化得到：

g取得最大值时，则认为此时T值为最合适的阈值。

2 仿真分析

2.1 滤波仿真与分析

针对AMGF-L 方案进行实验分析，在Visual Studio 2017 中实现，配合OpenCV 视觉库，为避免出现单一指标的误差使用10%椒盐噪声污染4 幅图像进行算法性能评价，通过主观分析和数据定量分析的方式进行比对。与采用掩码大小为5 的高斯滤波以及AMGF 进行对比，如图2～5 所示，发现AMGF-L可以去除图像中的大部分噪声，同时图像轮廓信息更加清晰。使用峰值信噪比（peak signal-to noise ratio，PSNR）［16］和 信 噪 比（signal-to noise ratio，SNR）评价边缘检测算法的性能，SNR和PSNR数值越大，图像失真越小。不同算法检测结果的SNR与PSNR如表1所示。

表1 不同滤波算法SNR与PSNR表现dB

图2 10%椒盐噪声滤波实验对比

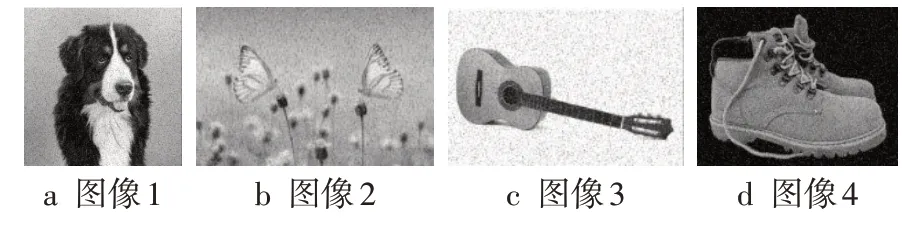
图3 高斯滤波滤波实验对比

图4 AMGF滤波实验对比

图5 AMGF-L滤波实验对比

2.2 边缘结果仿真与分析

选取数据集中4 种含有噪声数据的图像进行边缘结果实验仿真，对文中算法、经典Canny算法、Sobel 算子、文献［8］算法的边缘检测结果进行评价。经典Canny 算法高低阈值设定100和50，高斯滤波器大小为5，4种图像边缘结果如图6～9所示。

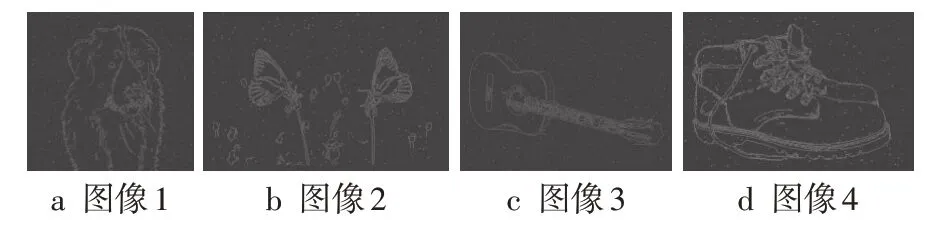
图6 经典Canny算法边缘结果对比

图7 Sobel算子边缘结果对比

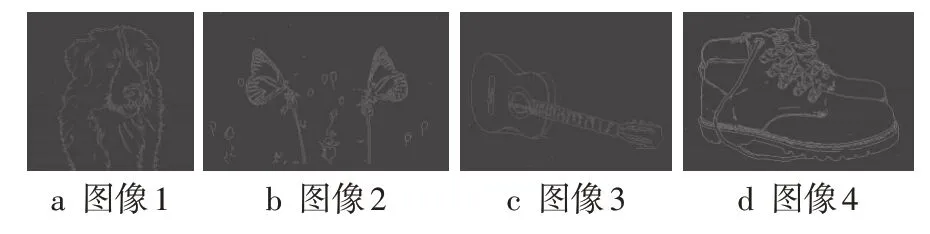
图8 文献［8］算法边缘结果对比

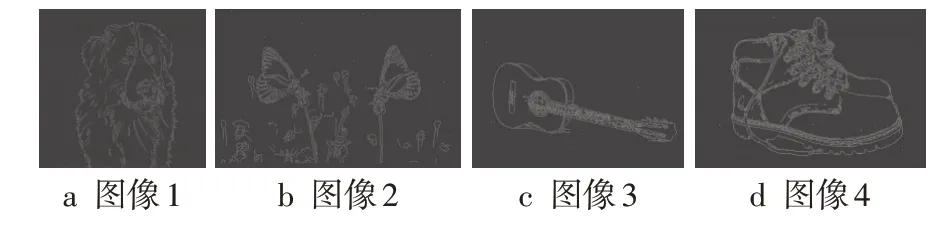
图9 文中算法边缘结果对比

从边缘结果来看，Sobel算子受噪声影响，得到的图像边缘出现了边缘连接线断连且边缘线较粗；经典Canny 算法相对Sobel 算子，边缘线定位更精确一些，依旧出现了边缘线不完整的现象；文献［8］算法较好地滤除了图像中的噪声，但滤波之后丢失了一些边缘细节信息，导致图像边缘完整性有一定程度的缺失；相较于上述3 种方法，文中算法去除噪声的能力较强，得到的边缘线连续且完整，可以提取出图像中较完整的边缘细节信息。

为直观体现算法性能的优劣，引入文献［10］中的评价指标，如表2所示，A代表边缘算法检测得到的像素总数，B代表图像中像素的4连通域，C代表像素的8连通域。C/A、C/B越小，图像边缘连续性越强，图像边缘检测质量越好。从表2 可看出，文中算法相较经典Canny 算法、Sobel 算子、文献［8］算法，C/A分别低0.07～0.24、0.11～0.22、0.06～0.11，C/B分别低0.06～0.14、0.07～0.16、0.06～0.11，表明文中算法具有一定的降噪保边能力，边缘检测效果良好，可以检测得到较完整的边缘。

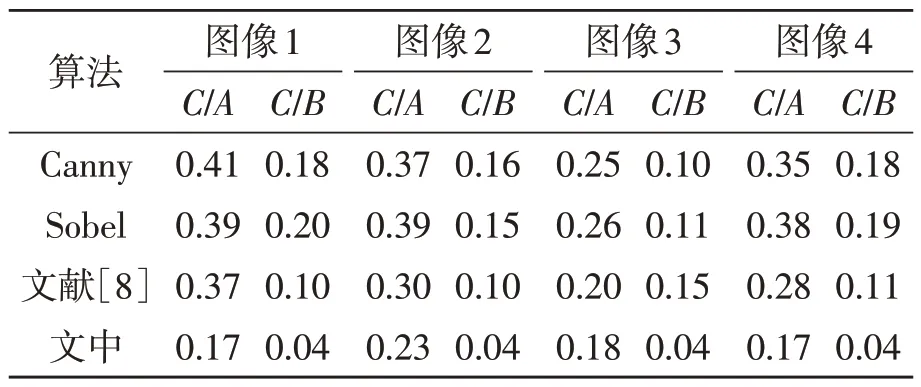
表2 各算法不同图像的C/A、C/B

使用BSD500［17］数据集中500 张不同种类的图片进行实验，性能指标为F1（F-measure），F1 越高代表对应的算法性能越好，结果见表3。相比经典Canny算法、Sobel算子及文献［8］算法，在无噪声条件下文中算法的F1 分别高4.2%、7.4%、2.8%；在10%噪声条件下文中算法的F1 分别高24.8%、27.5%、8.5%。从表3中可以看出，在有噪声影响的条件下，经典Canny 算法F1下降幅度较明显，文中算法F1下降幅度微小且远高于经典Canny 算法与Sobel 算子，好于文献［8］算法，证明了文中算法在噪声图像下的优越性。

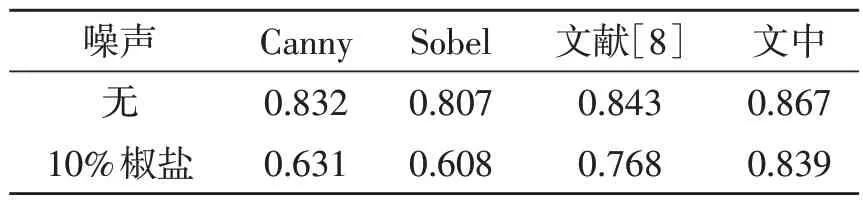
表3 BSD500性能测试

3 结论

经典Canny 算法无法抑制椒盐噪声且抑制噪声后无法保证图像边缘细节信息，为此提出使用AMGF-L方案替换高斯滤波，应用Scharr算子代替Sobel 算子得到高精度梯度图，保证自适应阈值方法的有效实施，最终经非极大值抑制技术连接边界得到图像边缘。以实验图像为例，去噪后图像的PSNR 相较其他算法提升了2.25～14.5 dB，边缘评价指标及F1 表现均优于其他算法。结果表明，改进Canny算法可以去除椒盐噪声，并有效保留图像边缘细节，为后续图像处理时目标区域定位识别等操作提供了准确的边缘轮廓信息。