基于响应矩阵的RFQ新调谐算法的验证与实现
2023-12-27陆羿行方文程张俊强郭玉森赵振堂
陆羿行 方文程 张俊强 郭玉森,5 赵振堂
1(中国科学院上海应用物理研究所 上海 201800)
2(中国科学院大学 北京 101408)
3(中国科学院上海高等研究院 上海 201204)
4(上海市低温超导高频腔技术重点实验室 上海 201800)
5(上海科技大学 上海 201210)
射频四极场加速器(Radio Frequency Qaudrupole,RFQ)[1-4]常用于低能质子的加速,可以保证其束流品质,如今广泛应用于质子加速器及相关装置中。现有装置上的RFQ工作频率通常在200~400 MHz,而欧洲核子中心(European Organization for Nuclear Research,CERN)研发的用于质子治疗装置的RFQ工作频率为750 MHz[5],这种高频率的RFQ具有更高的加速梯度,可以推动质子加速器的小型化。近十多年中,上海光源(Shanghai Synchrotron Radiation Facility,SSRF)也在致力于质子治疗装置的研发,为瑞金医院肿瘤质子中心设计、建造的首台国产质子治疗装置已经通过验收,进入临床试验阶段[6-8];同时,提出了基于直线加速器的质子闪疗装置[9-11],紧凑型RFQ作为装置中的一部分,也已经过了多年的研究。调谐是紧凑型RFQ的关键技术之一,传统的调谐算法基于腔体理论计算得到的物理特性,用于紧凑型RFQ效果欠佳。CERN在高频RFQ上利用实际场分布对调谐棒的响应量,即响应矩阵,来进行调谐[12-13],在求解的过程中应用了奇异值分解(Singular Value Decomposition,SVD)方法。然而,这种方法仍然存在不足,在求解过程中常常出现调谐量超出调谐棒可调节范围的情况,即使对SVD方法进行了改造解决了这个问题,又会造成精度下降,导致调谐步骤多、二极场分量难以降低等问题。
针对以上问题,本文提出了一种在响应矩阵的基础上利用最小二乘法(Least Squares,LS)进行求解的调谐算法。该算法可以限定求解的范围,得到其中的最优解;同时,对腔体的二极场分量赋予权重,可以有效地对二极场进行调谐,解决二极场误差难以降低的问题。基于这种新型的RFQ调谐算法,在Matlab下进行了算法的开发,完成了模拟条件下的调谐实验,搭建了基于微扰法的测量平台,编写了控制和通信的Labview程序,并在RFQ样机上完成了算法的最终验证。
经过实验验证,新调谐算法可以在限定范围内得到最优解,并有效地解决二极场误差。该算法具有普适性,可以应用到其他频率的RFQ中,解决更多RFQ的调谐问题;将来可以促进质子加速器的小型化,推动医用质子装置的发展,普及相关诊疗手段(质子治疗、质子CT(Computed Tomography)[14-15]、硼中子俘获疗法(Boron Neutron Capture Therapy,BNCT)[16]、医用同位素生产[17]等)。
1 RFQ及其测量方法
四翼型RFQ的腔体是在谐振腔的腔壁上添加4个极头形成的,其工作模式是类TE210模。在横向上,4个极头间可以激发出电四极场,腔体中的电场也主要集中在极头附近;在远离极头的位置,主要为磁场,方向沿轴向(图1(a))。当束流在轴线上通过时,会受到四极电场的聚焦作用,并且该电场的极性会随时间和粒子的位置变化,因此,每过半个射频周期粒子就会受到相反的作用。在纵向上,极头与轴线间的距离最小为a,最大为ma,m为调制参数。经过调制后,极头呈类三角函数的形状,形成纵向的电场,实现对束流的聚束和加速作用。极头形状变化的周期为βλ,相对极头的“峰”和“谷”是对应的,而相邻极头的“峰”和“谷”则是错开的(图1(b))。
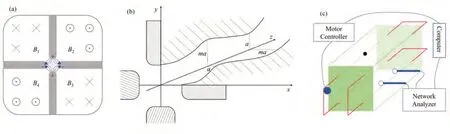
图1 RFQ结构及测量框架图(a) RFQ横向形状及电磁场分布,(b) RFQ极头纵向形状,(c) RFQ测量方法框架图Fig.1 Structure of an RFQ and the framework of the measurement(a) Transverse section of an RFQ and the electromagnetic field on it, (b) Longitudinal section of an RFQ, (c) Framework of measuring an RFQ
测量腔体中的场分布是RFQ调谐的第一步,可以利用微扰法实现。RFQ的最小束流孔径一般都非常小,在1~3 mm,难以测量其轴线上的电场分布,因此,RFQ是通过测量4个象限中的磁场来得到场分布的。用步进电机带动鱼线,鱼线又带动金属小球在腔体中运动,金属小球会对腔体中的电磁场分布产生影响,探针测量得到的S12信号也会发生改变,由此可以推算出小球所在位置的磁场强度,存在关系[18]:
式中:B表示磁场强度;ΔP表示小球的扰动引起的相位差。电机控制器和网络分析仪可以与计算机进行通信来传递数据(图1(c))。
2 基于响应矩阵和最小二乘法的调谐算法
加速器调谐的基本逻辑是利用调谐器对腔体的扰动,弥补腔体内场分布的误差。通过对腔体的测量,得到场分布及其与理想状态的差别,再利用腔体的物理特性,计算得到调谐器所需的调谐量。RFQ的主要调谐方法可以分为两大类:一种基于理论计算得到的物理特性,例如文献[19],可以称为“理论法”;另外一种基于实际测量得到的物理特性,例如文献[12-13],可以称为“解析法”。理论法的缺点在于把理想状态下计算得到的数据应用于实际,忽略了实际腔体和理想模型之间的差别;对于敏感度更高的紧凑型RFQ而言,实际情况与理想状态相差较大,因此理论法难以适用。解析法则可以消除理论和实际之间的误差对调谐造成的影响,可以解决紧凑型RFQ的调谐问题;解析法的缺点是需要额外测量响应矩阵。下面将详细介绍基于响应矩阵和最小二乘法的新调谐算法。
分别用B1、B2、B3、B4来表示各象限中的磁场(图1(a)),则可以计算得到腔体中的二、四极场:
式中:Q为四极场;Ds、Dt为两个方向上的二极场。在实际测量和计算中,以上场量均使用归一化值,其归一化误差定义为:
将二、四极场组合起来形成场矩阵:
式中:n为沿轴线取场的点数,并满足场矩阵中元素的数量大于等于调谐器数量,即3n≥ntuner,因为这样可以提高调谐的精度。RFQ初始状态的场矩阵记为Fi,接着分别移动每一个调谐器并重复测量对应的场分布,记为F1,F2,…,Fn-tuner,可以得到不同场分量对调谐器的响应,即响应矩阵:
式中:d为调谐器的移动量。对于一个理想的RFQ,需要四极场的值都相等,且二极场大小为0,即目标矩阵:
因此,调谐器对场分布的补偿量应为:
至此,调谐问题转化为求解方程:
式中:T即为需要求解的调谐量矩阵。
从上文可以发现,响应矩阵M通常为一个非正方形矩阵,因此无法直接求解。CERN使用SVD方法来求解,但该方法无法限定调谐量的范围,直接求解得到的调谐量非常大,超出调谐棒可调谐的范围,因此,在求解过程中将特征值向量中的部分元素代换为0。这种改造后的SVD方法虽然解决了结果的范围问题,但是舍去部分特征值会影响到结果的精度,并可能放大二极场误差难以减小的问题。
对SVD方法做尝试时发现了上述问题。针对结果的范围问题,可以利用最小二乘法对调谐量矩阵T中的每一个元素进行单独求解,得到这一元素在限定范围内使误差最小的值,可以用式(9)表示:
式中:tn为矩阵T中的第n个元素。依次求解矩阵T中的元素,并对这个过程进行迭代,直到所有误差达到预期的目标为止。
在这种方法中,还可以对二极场分量赋予权重,以解决二极场误差难以减小的问题,即将原方程变为求解:
式中:k为给二极场赋予的权重。
整个调谐算法如图2所示。以上为调谐实验过程中针对一些问题给出的新解法,下面从模拟和实验两方面阐述对新调谐算法的验证。
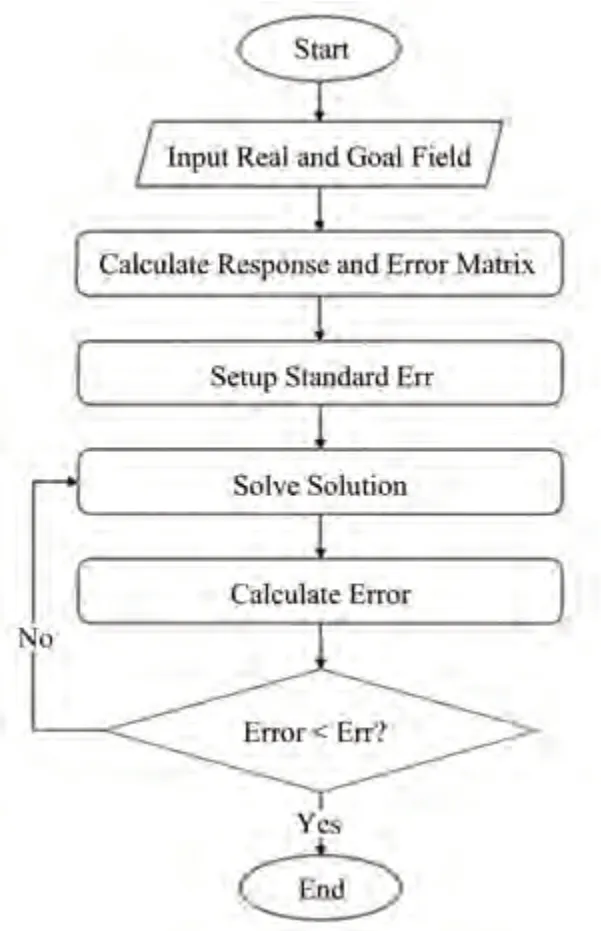
图2 基于响应矩阵和最小二乘法的调谐算法流程图Fig.2 Flowchart of the tuning algorithm based on response matrix and least squares method
3 基于模拟软件的调谐实验与算法验证
为验证新调谐算法,首先利用三维电磁场模拟软件进行了大量模拟调谐实验。RFQ的三维模型基于上海光源设计的714 MHz RFQ,在正式设计中,该RFQ的长度为2 m,可以将质子从50 keV加速至4 MeV,而用于模拟实验的模型长为1 m,横截面形状与正式设计相似。RFQ的实验模型如图3(a)所示,为金属模型,在该腔体上共有16根调谐棒,如图中所指部分,其余为耦合器、真空口及探测器预留位置。为实验模型重新设计了底切,在所有调谐棒均插入5 mm深的状态下,将其频率调至714 MHz,且将场分布调至理想状态。读取腔体4个象限中的磁场分布,在不同象限中读取的位置是对称的,其中一个位置如图3(b)所示。对场分布处理后,得到腔体的二、四极场分布如图3(c)所示,即为理想状态。图中四极场上的“x”标记为后续调谐实验过程中,选取场值用于调谐算法的位置,即n=6。
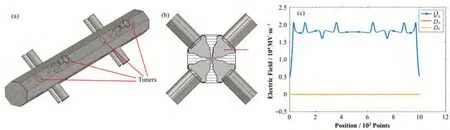
图3 模拟条件下RFQ的模型及场分布(a) RFQ模型,(b) RFQ截面图及选取场分布位置示意,(c) RFQ二、四极场分布(Qo为四极场,Ds、Dt分别为水平和竖直方向的二极场)Fig.3 3-D model of the RFQ and its field distribution in simulation(a) Model of the RFQ, (b) Transverse section of the RFQ and the place where the field was picked, (c) Dipole and quadrupole components of the RFQ
根据算法在Matlab中编写了相应的程序。在理想状态下,将每根调谐棒的插入深度分别减少和增加3 mm,重复获取模型中的场分布,得到每根调谐棒在6 mm范围内对场的影响,计算出的响应矩阵为18×16的矩阵。
3.1 单调谐棒扰动模拟调谐
首先进行单调谐棒扰动模拟。在理想状态下,将第一根调谐棒t1的深度增加2 mm,对场产生扰动,破坏理想状态,通过基于响应矩阵和LS方法来对场进行模拟调谐实验。
在单根调谐棒扰动的情况下,虽然在算法中加入了对调谐量范围的限制,但是在实际计算的过程中并未出现解出的调谐量大于调谐棒可调谐范围的情况。在给二极场误差加上不同的权重后,对比得到的结果可以发现(图4),随着权重的增加,调谐棒t1的解越接近-2 mm;而不论权重如何变化,其他调谐棒解出的调谐量绝对值均非常小,都在0.1 mm以内。由于在数值上该结果就已经十分接近扰动量,因此没有再将该结果应用到模型中进行模拟。基本可以推论,仅通过一次调谐,这些误差就已经大幅降低。
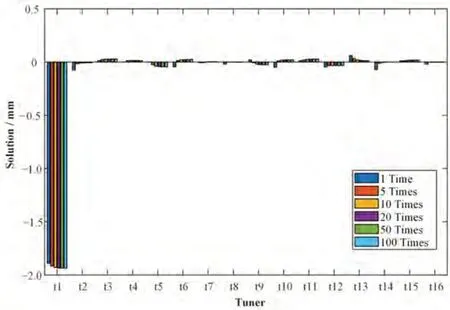
图4 单调谐棒扰动下不同权重得到的调谐量Fig.4 Solution with the different weight for dipole components under single tuners' perturbation
通过单调谐棒扰动下的模拟调谐,初步验证了调谐算法的可行性,并且实现了较为精准的调谐效果。
3.2 多调谐棒扰动模拟调谐
单调谐棒扰动实验初步验证了算法的准确性,但这种误差情况与实际不符,因此进一步进行了多调谐棒扰动模拟。通过在[-3 mm,3 mm]范围内生成随机数,为每一根调谐棒赋予了“扰动”,作为调谐的初始状态。调谐过程中的归一化误差用下式定义:
初始的二、四极场分布如图5(b、c)所示,初始的二极场误差较大,接近30%。
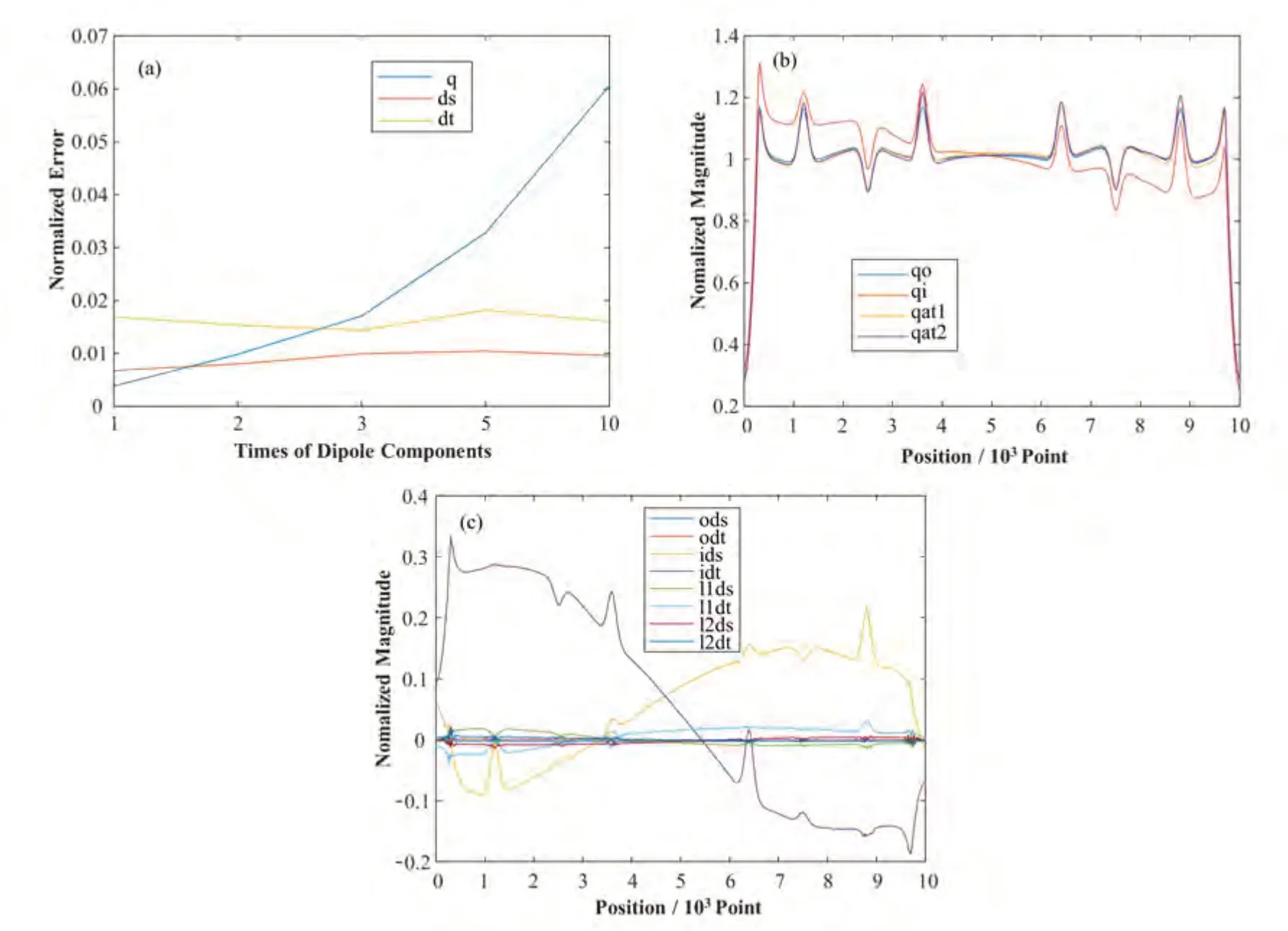
图5 模拟调谐实验结果及对比(a) 不同权重下得到的二、四极场误差比较,(b) 调谐过程中四极场分布比较,(c) 调谐过程中二极场分布比较Fig.5 Result comparisons of the tuning experiment in simulation(a) Quadrupole and dipole component errors with different weights, (b) Quadrupole field variation during the tuning,(c) Dipole field variation during the tuning
同样利用LS调谐算法来进行调谐。首先比较了二极场误差不同权重下的结果(图5(a)),图5中q为四极场误差,ds、dt分别为水平和竖直方向的二极场误差。与单调谐棒扰动的情况不同,当二极场误差权重达到5之后,四极场误差明显增长,迅速增长到2%以上,当权重增加到10以后,误差达到了6%。为了详细了解权重对结果的影响,补充了权重为2、3的结果,可以发现这两种情况下,四极场误差会有所增长,同时二极场误差会降低,并且在这个范围内,四极场误差均不超过2%,二极场误差也均在2%以内。几种权重相比而言,2倍的权重可以在保证较小的二极场误差的同时,让四极场误差在1%左右,是比较好的结果。以上模拟实验表明,多调谐棒扰动的情况和单调谐棒是有明显区别的,多调谐棒扰动下进行模拟调谐会更加接近实际情况,同时也说明为二极场误差赋予权重的方法仍然是有效的。
进一步地,在权重为2的调谐结果的基础上进行了第二次调谐,在第二次调谐中,赋予二极场误差的权重依旧设为2。两次调谐结果,以及初始场、目标场的比较见图5(b、c)。图5中,q为四极场误差,ds、dt分别为水平和竖直方向的二极场误差,前缀o表示目标场,i表示初始场,l1表示第一次调谐后结果,l2表示第二次调谐后结果。从图5中可以发现,经过一次调谐后,四极场分布已经和目标十分接近,同时二极场误差大大减小。经过两次调谐后,二、四极场误差均又在缩小,最终四极场误差为0.8%,二极场误差为0.4%,是非常理想的误差水平。
经过多调谐棒扰动模拟调谐实验,完全验证了调谐算法的可行性,验证了二极场权重对消除二极场的作用,预示着调谐方法在实际调谐中的优秀效果。
3.3 LS解法与SVD解法比较
对基于SVD解法的调谐算法也进行了简单验证。不可避免地,通过SVD解法得到的调谐范围很大,远远超出了调谐棒的可移动范围,必须利用改造后的SVD方法。根据算法,一共可以得到16组结果,其中前几组结果存在同样的问题,而后几组结果又存在丢失精度过多的问题,因此挑选了其中第9组来进行调谐。经过调谐后场分布误差有明显改善,四极场误差在1%以内,最大二极场误差约2%;第二次调谐依旧选用第9组结果,经过第二次调谐后,二极场误差减小(0.8%),而四极场误差增大(2%)。通过SVD方法两次调谐后四极场误差偏大,必须经过更多的调谐次数来减小误差;而应用二极场误差权重加LS方法,如上一节所述,两次调谐后实现了较为理想的场分布。
最终SVD方法和LS方法得到的二、四极场误差比较如图6所示,通过比较结果,验证了LS方法可限定求解范围、高效处理二极场误差、缩短调谐过程等优点。
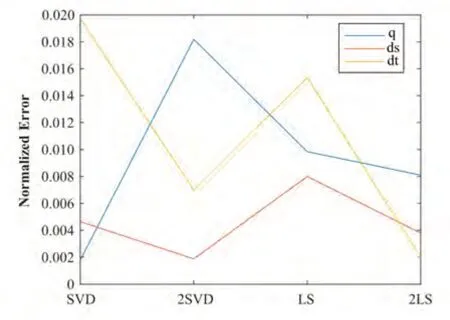
图6 不同调谐算法下二、四极场误差对比Fig.6 Comparison of the quadrupole and dipole component errors with different tuning methods
4 基于RFQ样机的调谐算法验证
以上完成了调谐算法的初步验证,根据模拟调谐实验的RFQ模型,加工了一段铝模样段(图7(a)),利用RFQ样机进一步验证调谐方法。
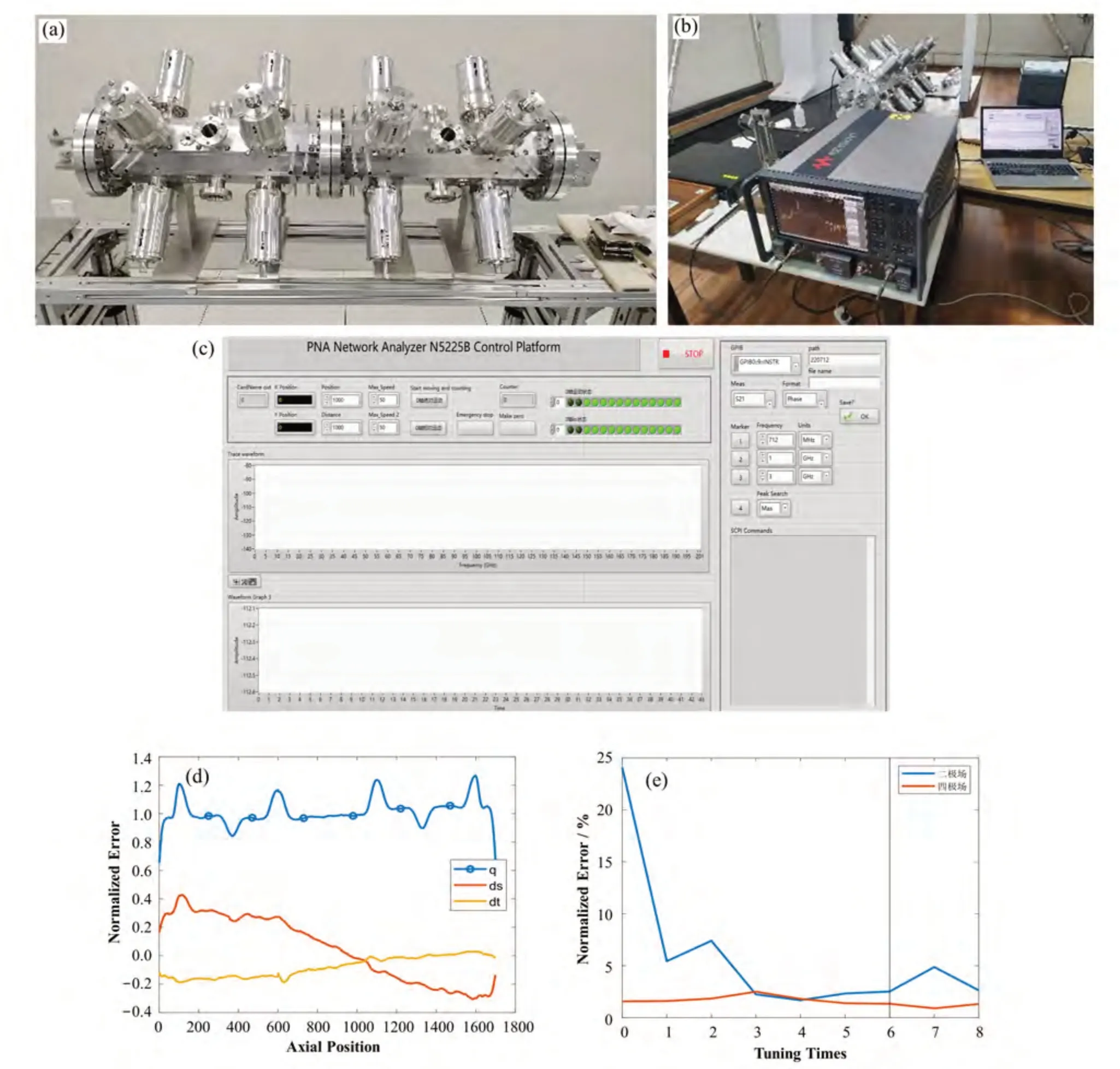
图7 RFQ样段调谐平台及实验结果(a) 714 MHz RFQ样机,(b) RFQ测量平台,(c) 电机控制和微波测量程序面板,(d) RFQ样段初始场,(e) 调谐过程中二、四极场误差变化Fig.7 Testbed of the RFQ prototype and the experimental results(a) Prototype of the 714-MHz RFQ, (b) Testbed of the prototype, (c) User interface of the motor control and RF measurement,(d) Initial field of the RFQ prototype, (e) Variation of quadrupole and dipole component errors during the tuning
RFQ的测量方法如§1所述,具体平台搭建见图7(b)。在RFQ样机的端板上开有4个测量孔,分别在RFQ的4个象限,鱼线带着金属小球在4个象限中来回穿过,并绕过固定在端板上的滑轮,利用步进电机带动小球在腔体中匀速运动。通过腔体上预留的耦合孔、真空抽口以及探测器孔将探针伸入腔体内,探针的另一头连接到矢量网络分析仪,获取腔体中的微波参数。步进电机控制及网络分析仪的数据传输均通过在LabView环境下编写的程序来实现(图7(c))。测量得到的数据先进行预处理,再利用调谐算法完成调谐量的计算,数据处理及计算均通过Matlab程序实现。RFQ样机上有16个调谐器,调谐器中螺杆带动调谐头移动,可以实现较为精准的调谐量。
对RFQ样段的初始场进行测量。先将每个调谐器的插入深度都调节为5 mm,使用两根探针测量腔体内的微波参数,处理后得到RFQ样段的初始场分布,其中,二极场误差在30%以上(图7(d))。主要原因在于初始状态调谐器的深度不一致,误差主要来源于两方面:一是调谐器与腔体间没有焊接,导致调谐器与腔体的间隙不一样,存在误差;二是调谐器的精度未达到预想的程度,难以判断各调谐器的深度是否一致。以上误差只会影响初始误差,不会影响调谐过程,因此在此样段上进行调谐实验来验证算法及调谐平台的可靠性仍是可行的。
利用上述调谐算法对RFQ模型腔进行调谐。初始状态下二、四极场误差分别为24.09%和1.57%,经过5次调谐后两者误差分别降为2.33%和1.39%。此时误差已经达到理想的水平,对腔体进行了一次频率调谐,即将所有调谐器的深度增加0.6 mm,二、四极场误差产生轻微变化,为2.52%和1.34%(图7(e)划线处)。之后又进行了2次额外的调谐以验证调谐算法的收敛性,结果显示误差在小范围振荡,可能是误差较小的结果已接近调谐算法的极限精度。调谐各步的误差结果见图7(e)。
5 结语
针对高频率、紧凑型RFQ在调谐过程中遇到的问题,提出了一种基于响应矩阵和最小二乘法的新调谐算法,可以在调谐棒可调节范围内求出最优解,且为二极场分量增加权重可以高效地减小二极场误差。在模拟环境下进行了调谐实验,初步验证了新调谐算法的可行性,与SVD解法的比较中体现出了新调谐算法的优势。根据调谐算法编写了Matlab程序,基于Labview开发了RFQ的测量和调谐平台,通过RFQ样机的调谐实验进一步验证了调谐算法。这种调谐算法是针对高频率、紧凑型RFQ开发的,同时也具备很强的普适性,适用于其他频率的RFQ,将来可以促使紧凑型RFQ应用在更多质子加速器装置上,推动医用质子装置的普及。
作者贡献声明陆羿行负责研究的提出及设计、数据的收集和整理、文章的起草和最终版的修订;方文程负责项目的监督和管理、文章的修订;张俊强负责实验数据的收集;郭玉森负责实验数据的收集;赵振堂负责项目的监督和管理、文章的修订。
