基于改进UNet模型的截断脉冲高度估计器

唐琳 周爽 廖先莉,2 刘泽 李波

1（成都大学 电子信息与电气工程学院 成都 610106）

2（成都理工大学 核技术与自动化工程学院 成都 610059）

3（南洋理工大学 电气与电子工程学院 新加坡 639798）

能谱测量的能量分辨率受脉冲高度估计精确度的影响，而脉冲高度估计的难点就是对畸变脉冲的估计。当测量系统输出的核脉冲宽度没能达到数字处理单元对脉冲宽度的最低要求时，这样的脉冲被称为截断脉冲。截断脉冲作为畸变脉冲的一种，经过放大和整形，在数字化过程中得到了失真的脉冲高度，对这些脉冲高度采用多道分析器（Multichannel Analyzer，MCA）进行分析，每一个脉冲高度都对应着相应道址上的一次计数，当测量系统输出的脉冲因宽度不足而产生幅度损失时，该脉冲对应的计数道址就会向左发生漂移。当这类脉冲的数量足够多时，它也扭曲了测量得到的光谱，文献［1］对成谱原理及过程进行了详细分析。

近几年，作为光谱学领域以及辐射测量领域的研究热点，国内外学者发表了很多关于脉冲畸变、脉冲堆积的改进方法，可以概括为脉冲形状甄别以及脉冲幅度计算两个类别。从脉冲形状甄别上来看，用于截断脉冲最简单、高效的方法是脉冲剔除，作者在文献［1］中详细陈述了关于截断脉冲剔除的方法以及剔除的结果分析，与此同时，该方法也存在净计数损失的缺陷，因此，在后期的研究中又提出了脉冲衰减时间修复［2］、上升时间修复［3］、多脉冲局部成谱［4］等算法来对计数进行补偿。针对脉冲畸变，除了剔除与修复以外，也有学者提出将基于脉冲形状的数学模型并将其应用于γ射线光谱中［5］或将基于数值方法的滤波器模型应用于中子γ监测［6］，这两种方法都能够有效消除光谱失真，但也存在对脉冲形状限制较为严格的缺陷。另一方面，传统的脉冲幅度计算最常用的方法是数字整形滤波，包括三角整形［7］、梯形整形［8］、高斯整形［9］、双指数脉冲响应整形［10］、CR-RC整形［11-12］以及准高斯脉冲整形［13］。这些数字整形方法对于绝大部分脉冲的幅度计算都能实现较高的精度，但对于本文所提的截断脉冲，当脉冲宽度严重不足时将会对脉冲高度的计算产生较大的影响。

近年来，深度学习技术发展迅猛，这为脉冲高度估计提供了新的思路。众所周知，脉冲高度估计最简单有效的方式是通过高精度模数转换对核脉冲信号进行数字采样来实现线性展开（Linear unfolding），然后，通过寻峰算法搜索每个脉冲的峰值作为脉冲高度值［14-15］，但该方式对各种类型的噪声都不具备免疫能力。为了避免这个问题，也有学者尝试进行在非线性滤波器的设计［16］，但设计过程较为复杂。

基于上述原因，本文旨在实现一种兼顾信噪比与脉冲高度估计的复合神经网络模型，考虑到UNet已经作为滤波器模型被成功应用在音频源分割［17］，本文以UNet的编码-解码为基本框架并添加了一个对时序更为敏感的长短期记忆模型（Long and Shortterm Memory，LSTM）。LSTM作为一种特殊的递归神经网络（Recursive Neural Network，RNN），适用于在时间轴上有相关性的事件预测，前期已经被成功应用于堆积脉冲的识别与分离［18-20］。本研究展示了一个由多模型进行复合产生的神经网络模型的拓扑结构和训练过程，该模型用于对测量系统输出脉冲进行反卷积展开，从而在不忽略信噪比的情况下实现脉冲高度的准确估计。

1 数据集制作

本文提出的UNet+LSTM模型用于对硅漂移探测器输出的截断脉冲进行高度估计。硅漂移探测器输出的弱电流信号经开关复位型的前置放大电器放大后输出堆积上升的阶跃脉冲，如图1所示。

图1 前置放大器的输出信号Fig.1 Output signal of a preamplifier

从图1可以看出，前放输出的阶跃脉冲不仅是堆积上升的，而且还包含很多噪声。因此，在制作模拟数据集的时候，为了对脉冲幅度进行归一化处理，用于产生脉冲幅度的随机数X1服从0~1之间的均匀分布，用于产生噪声幅度的随机数X2服从0~0.05之间的均匀分布，其数据集制作过程如图2所示。堆积上升的阶跃脉冲叠加噪声后然后再由CR微分整形器滤除直流成分并将阶跃脉冲整形为负指数脉冲。负指数脉冲序列经数字化采样建模产生矩阵形式的数据集［21］。

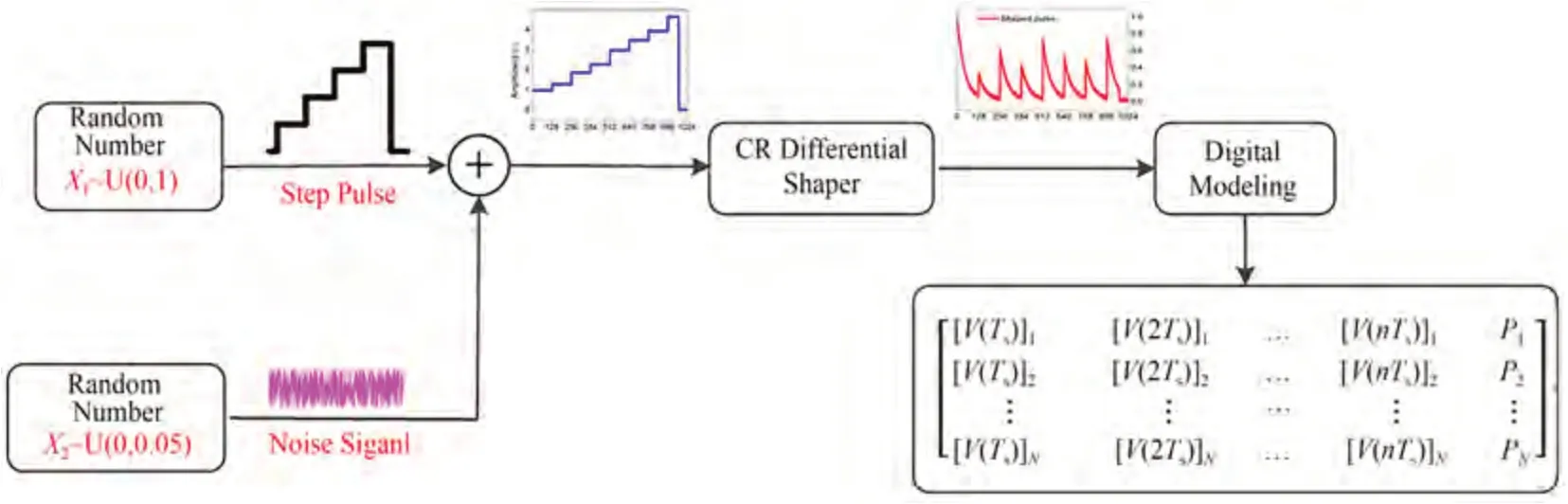
图2 数据集制作过程Fig.2 Generation process of datasets

为了得到完整的负指数整形脉冲，阶跃脉冲需要有一定的保持时间，当采样频率为50 MHz、采样点数为128点时，每个阶跃脉冲的理想宽度为6.4 μs。但实际测量中测量系统输出的阶跃脉冲常常会包含一些宽度不够的脉冲，如图2中阶跃脉冲序列中的最后一个脉冲所示，本文把这种脉冲宽度不足的脉冲定义为截断脉冲。这种脉冲在经过CR微分整形后将会以被截断的负指数脉冲形式呈现［22-24］，如图2中负指数脉冲序列中的最后一个脉冲所示。

将CR整形后的结果进行采样，采样周期Ts为50 MHz，采样点数128点，生成的脉冲幅度矩阵如式（1）所示。矩阵包含N行n+1列，其中：N代表脉冲数量，n代表每个脉冲的采样点数，取值128。因此，矩阵（1）中每一行代表一个脉冲的128个采样幅值以及该脉冲的真实高度。以第一个脉冲为例，第一行前128列代表该脉冲的128个采样值，最后一列P1代表第一个脉冲的脉冲高度。根据模型训练需要，本文将数据集按照7∶2∶1的比例分割为训练集、验证集、测试集［25］。

为了评估截断脉冲数量对本文所提议模型性能的影响，引入截断率指标Rt，Rt表示截断脉冲数量占总脉冲数量的比例。在数据集的制作中，生成截断率不同的噪声脉冲序列1 000个，每个序列包含4个脉冲，而每个脉冲由128个采样点组成，因此，在模拟数据集中1 000个脉冲序列生成了512 000个样本。在实际测量中得到的脉冲序列其截断率通常会随着计数率升高而升高，但通常都在25%以下，因此，在进行截断率分配的时候重点关注了25%以下的比例，模拟产生的数据集中，截断率5%、10%、15%、20%、25%、35%、45%、50%、75%和100%的脉冲序列各占比10%。

2 模型开发

本文提出一种改进的UNet模型，其内部结构如图3所示，使用§2生成的数据集训练模型。在模型训练过程中，输入信号是叠加了噪声的脉冲幅度矩阵，而输出信号则是被展开的脉冲高度集合。该网络包括提取信号特征的编码器以及进行特征融合的解码器，不管是编码器还是解码器都包含4个卷积核大小为3×3的卷积块，不同之处在于编码器在卷积层之后使用最大池化运算进行下采样，池化大小为2×2，步长为2，而解码器则是先通过2×2转置卷积运算对输入信号进行上采样，减少特征通道数，然后再进行卷积运算。区别于传统UNet的是改进后的UNet在编码器和解码器之添加了LSTM，LSTM输出的是特征值，因此，在特征值与损失函数之间还需要用一个全连接层进行连接。

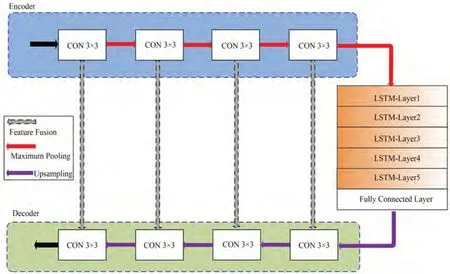
图3 UNet-LSTM模型结构示意图Fig.3 Structural diagram of UNet-LSTM model

为了评估模型输出和期望输出之间的差异，均方差（Mean Square Error，MSE）被用作模型的损失函数并将损失值LMSE反馈给网络来更新权重，实现减少后续迭代误差的目的。模型输出值脉冲高度集P'i与预期的输出值Pi的误差则可以通过损失函数来计算。对于有N个样本的训练集，损失函数的计算式如式（2）所示：

图4显示了模型训练过程中LSTM的层数和batch_size的超参优化过程，使用Adam优化器，采用可变学习率对模型进行训练，初始值为0.000 1，在1×10-5~1×10-3区间内动态更新。如果batch_size设置得太大，可能会导致训练过程中内存溢出，并且模型容易收敛到局部最优，从而无法完成训练；如果batch_size太小，则模型的收敛速度太慢，训练时间太长。图4显示了当LSTM模型的层数为5且参数batch_size分别设置为10和100时，在训练集和验证集上获得的迭代损失值。当batch_size为100时，模型在第40个epch收敛，收敛后的损失值依然高达1.8×105；当batch_size设置为10时，模型正常收敛，并且收敛后的损失值能够快速下降。

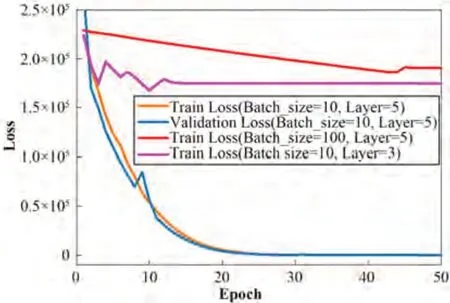
图4 UNet-LSTM模型训练过程中的损失值变化（彩图见网络版）Fig.4 Changes in loss values during the training of the UNet-LSTM model (color online)

在对LSTM模型进行参数优化时，理论上讲，层数越多训练结果就越理想。当然，梯度消失的问题也需要考虑，层数的增加会带来更大的计算负担，因此在优化超参时通常将层数设置为3~6。图4显示了LSTM层数分别为3和5时在训练集上获得的损失值迭代图。可以看出，当batch_size为10时，LSTM模型即便层数不同但衰减速度是接近的，但当层数为3时，模型收敛后的损失值仍然高达1.6×105；当层数为5时，模型不仅能够快速收敛，而且收敛后的损失值也会快速降低。

3 模型性能评估

3.1 模型验证

取验证集中200个脉冲序列中任意5个序列进行分析，如图5所示，每个序列包含4个脉冲，且脉冲幅度都在0~1之间，其中序列S1包含脉冲P1~P4，截断脉冲为P3；序列S2包含脉冲P5~P8，截断脉冲为P6和P7；序列S3包含脉冲P9~P12，截断脉冲为P9和P11；序列S4包含脉冲P13~P16，截断脉冲为P14；序列S5包含脉冲P17~P20，截断脉冲为P18和P19。

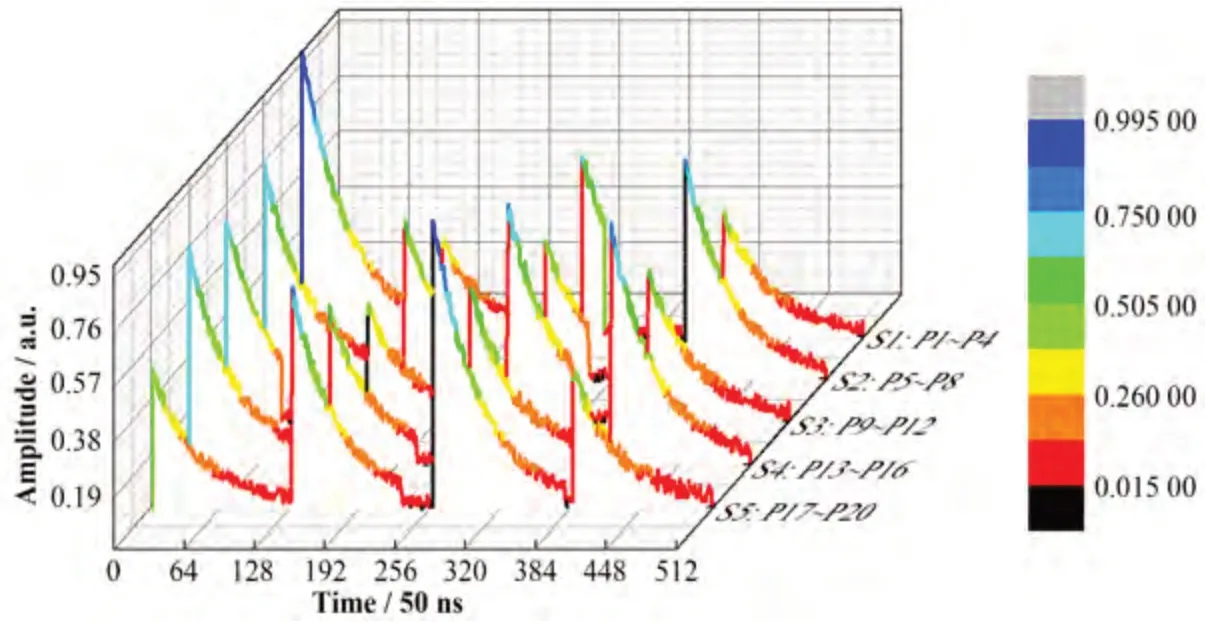
图5 模拟脉冲序列图Fig.5 Simulated pulse sequence diagram

为了验证模型脉冲高度估计的性能，对图5所示的20个脉冲分别采用传统的数字梯形成形方法和复合神经网络模型进行脉冲高度预测。取序列S1中4个负指数脉冲如图6中的红色曲线所示，截断脉冲P3在衰减过程中发生了截断，损失了截断之后的所有脉冲幅度信息，导致成形结果的幅度有较大的损失。

图6 梯形成形结果（彩图见网络版）Fig.6 Trapezoidal shaping result (color online)

在对模型和梯形成形结果进行对比时，用Δ表示脉冲高度估计的绝对误差，δ表示相对误差，Areal表示真实脉冲高度，ATrape表示通过梯形成形算法得到的脉冲高度，从而得出梯形成形对脉冲高度估计的绝对误差ΔTrape和相对误差δTrape的计算公式分别如式（3）和（4）所示，AUNet表示UNet-LSTM模型预测得到的脉冲高度，UNet-LSTM模型对截断脉冲高度估计的绝对误差ΔUNet和相对误差δUNet的计算公式分别如式（5）和（6）所示。

对图5所示的20个脉冲采用传统的梯形成形算法以及本文提议的神经网络模型分别进行脉冲高度分析，结果如表1所示。如前文所述，当采样频率为20 MHz，采样周期为50 ns时，一个完整的负指数脉冲包含128个采样点，理想脉冲宽度为6.4 μs。图5所示的发生截断的脉冲包括P3（包含20个采样点）、P6（包含30个采样点）、P7（包含40个采样点）、P9（包含50个采样点）、P11（包含60个采样点）、P14（包含80个采样点）、P18（包含100个采样点）、P19（包含120个采样点），对该脉冲序列进行梯形成形，梯形成形的上升时间包含30个采样点，持续时间为1.5 μs，平顶宽度为3.4 μs。

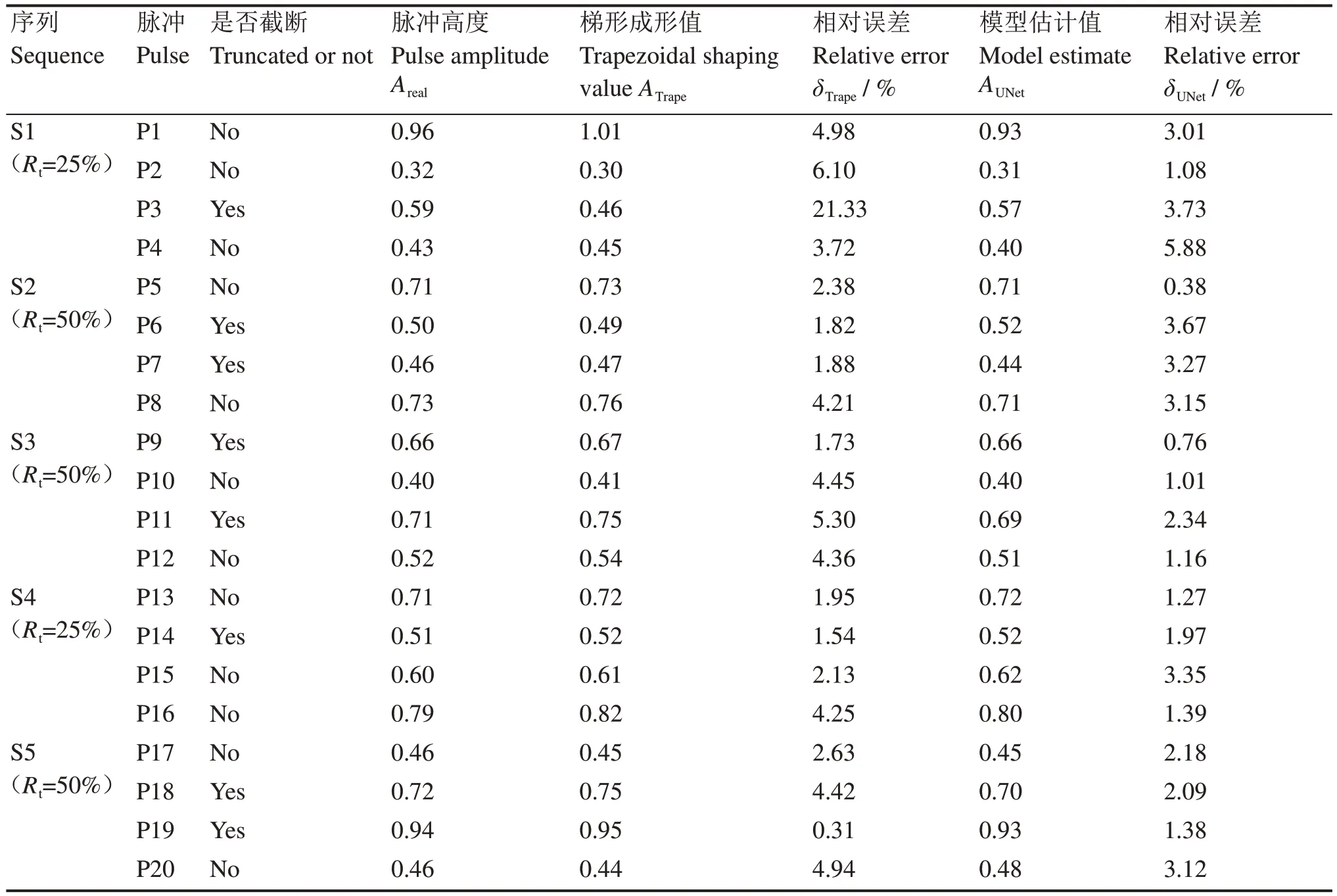
表1 神经网络模型对截断脉冲高度的估计值与真实值的对比Table 1 Comparison between the estimated and true values of the pulse height using neural network models

在前期研究成果［2］中已经得出传统的成形算法要求负指数脉冲宽度至少大于三角成形或者梯形成形的上升时间，否则得到的成形结果就会产生较大的误差，因此，本文在采用梯形成形时选择了较小的上升时间来尽可能地避免成形误差产生。从表1中梯形成形对脉冲高度的计算结果可以看出，8个截断脉冲中仅P3的脉冲宽度小于梯形成形的上升时间，其梯形成形结果相对误差高达21.33%，而其他截断脉冲的相对误差都能够控制在5%左右，最终梯形成形算法对该序列脉冲高度估计的平均相对误差为4.22%。采用UNet-LSTM模型对输入脉冲序列进行展开并进行脉冲高度估计，可以看出，估计结果并未受到脉冲截断的影响，平均相对误差约为2.31%，该模型对验证集中200个脉冲序列进行高度估计得到的平均相对误差约为2.18%。

3.2 实验结果分析

为了在实际应用中对所提出的神经网络模型进行验证，在规定的实验条件下，截取相同样品不同截断率的脉冲序列以及不同样品相同截断率的脉冲序列调用神经网络模型进行脉冲高度估计，其实验结果如表2所示。表2展示的8个脉冲序列是从实际测量得到的离线脉冲序列中截取的，其实验平台的配置如下：

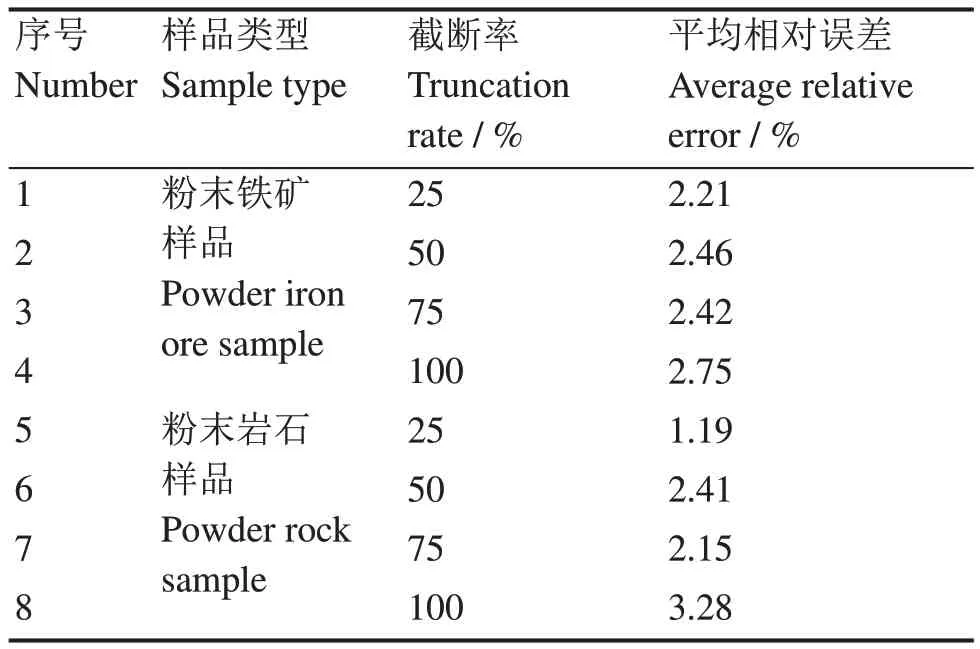
表2 神经网络模型对不同样品的脉冲高度估计效果对照表Table 2 Comparison of the pulse height estimation effects of neural network models on different samples

1） KYW2000A型X光管，带有Ag target的X射线管被用来辐照样品，X射线管的电流被设定为8 μA，电压保持在35 kV；

2） FAST SDD探测器（123 eV FWHM Resolution @ 5.9 keV）；

3） 粉末铁矿样品、粉末岩石样品；

4） 数字系统采用ADC9235，工作在20 MSPS，分辨率为12位。

其中：FAST SDD如图7（a）所示，X光管如图7（b）所示。

图7 实验装置图片 (a) 探测器，(b) X光管Fig.7 Photographs of experimental setup (a) Detector, (b) X-ray tube

为了保守地测试本文所提的神经网络模型，测试集截取的负指数脉冲输入信号比训练集和验证集中的输入信号噪声更大。探测器输出的阶跃脉冲信号经开关复位型前置放大器和CR微分整形电路输出负指数脉冲序列，经数字化后将获得的脉冲序列输入UNet-LSTM模型进行脉冲高度估计的离线处理。从两种样品多次实验获得的离线脉冲中分别截取截断率为25%、50%、75%、100%的实测脉冲序列进行模型预测结果分析，结果如表2所示。

8组脉冲序列中，样品类型不同、截断率不同都没有对神经网络模型的脉冲高度估计结果有任何影响，即便是在截断率高达100%的极端情况下，本文训练的神经网络模型依然获得了远优于传统脉冲估计方法的性能，在两种样品、8组离线脉冲序列的幅度估计中得到的平均相对误差为2.36%。

4 结语

在这项研究中，提出改进的UNet模型对脉冲高度进行估计，该模型在UNet结构的基础上添加了LSTM，以模拟生成的脉冲序列作为数据集对本文提议的神经网络模型进行训练和验证。验证集上的损失值在下降过程中出现了震荡，最终在第46个epoch时验证集和训练集的损失值都达到了10-4的数量级，模型收敛良好。在模型验证环节中，取5个脉冲序列进行脉冲高度估计，其中UNet-LSTM模型对脉冲高度估计的平均相对误差约为2.31%，相较于传统的梯形成形算法对脉冲高度估计得到的平均相对误差降低了1.91%。在粉末铁矿样品和粉末岩石样品的实际测量中，不同截断率的实测脉冲序列也进一步验证了UNet-LSTM模型的脉冲高度估计性能，在两种样品、8组离线脉冲序列的幅度估计中得到的平均相对误差为2.36%。模拟与实验结果表明，该模型能够准确地对发生了截断的脉冲序列进行脉冲高度估计。

本文提出的神经网络模型并不仅是针对特定的探测器，在今后的研究中，将重点考虑将该模型应用于快速光谱学，通过准确预测脉冲高度来改善光谱学分析性能，这对于光谱精细化分析以及元素含量分析都是具有重大意义的。

作者贡献声明唐琳负责论文整体构思，初稿完善；周爽直接参与论文研究，负责模型训练；廖先莉负责数据集制作；刘泽负责实验暑假数据的收集与整理；李波负责实验测试结果分析。