分数阶计算机病毒模型的稳定性与分岔分析

鞠雅雯,肖敏†,丁洁,杨鑫松

(1.南京邮电大学 自动化学院、人工智能学院,江苏 南京 210023;2．四川大学 电子信息学院,四川 成都 610065)

计算机病毒是一种能够通过自我复制或者自我延伸来入侵他人电脑并破坏计算机系统的程序代码,其具有潜伏性、破坏性、传染性、寄生性和隐蔽性等特点[1],这些病毒主要通过互联网从一台计算机传播到另一台计算机。存在各种类型的计算机病毒,它们不仅已经成为计算机用户的主要威胁,也成为网络资源的主要威胁[2]。随着信息技术的快速发展,网络信息资源已渗透到社会生活的各个领域,计算机技术在信息管理中的应用效果有着重要的影响,依靠计算机创新信息管理方式,可以不断优化信息管理系统,提高信息应用集成的标准化,更好地将计算机技术有效应用到信息管理的各个平台[3-4]。

计算机病毒会直接作用于系统内部,并在相对稳定的情况下直接扩散到另一载体中,从而达到将病毒扩散到全部系统的目的,最终导致众多计算机技术应用领域遭受严重损失[5],给社会安全造成巨大危害。2017年,WannaCry病毒在世界多个国家和地区大爆发,给政府部门、企业单位和教育机构等关键设施造成难以估计的损失[6]。随后出现的新型勒索病毒Petya在欧洲迅速蔓延,破坏性比传统的病毒更大[7],导致社会产生严重的危机管理问题。近年来,国内外诸多学者都致力于研究病毒在计算机网络中的传播机理[8-11],其中有关Hopf分岔的研究取得了许多重要成果[12-15]。于振华等[16]运用稳定性理论与Hopf分岔定理研究了恶意软件的传播动力学,并深入分析了控制参数对分岔点的影响。Li等[17]考虑了具有非线性发生率的病毒传播模型,将原有的三维系统拓展到四维,分析了平衡点的稳定性,推导出Hopf分岔的规范形式,得到了分岔周期解的稳定性条件。吴三柱等[18]建立了改进的病毒传播动力学模型,新增了病毒节点在网络传播中的通信半径、移动和停留两种状态,并进行了平衡点存在性和稳定性分析。陈实等[19]针对Hopf分岔导致的恶意病毒传播扩散,采用了参数调节法和状态反馈法相结合的混合分岔控制策略,并探明分岔阈值与控制器增益参数之间的关系。

然而目前针对计算机病毒的分数阶模型并不常见,在传统的病毒模型研究中也很少考虑到时滞对系统的影响。分数阶涉及积分和借助分数微积分的横切微分,与普通整数阶相比,分数阶为描述不同物质的记忆和遗传特性提供了强有力的工具,可以更好地帮助学者们理解对现实世界问题的解释,也有助于真实现象的建模,这是分数阶模型与整数阶模型相比最显著的优点[20-21]。随着分数阶微积分的蓬勃发展,分数阶系统的控制和Hopf分岔问题近年来受到了越来越多的学者的关注。此外,复杂系统中的时滞现象不容忽视,某个不起眼的时滞也有可能影响到整个系统的稳定性。通过将分数阶导数与时滞相结合来分析系统的状态能更加符合实际,因此研究分数阶时滞动力学系统的特征有着十分重要的理论和实践意义[22]。

传统的病毒模型中并未考虑时滞对系统的影响,更多的文献也仅考虑了潜伏期这种单一时滞对系统带来的影响。并且用传统的整数阶导数刻画模型,无法反映系统变量之前的状态信息,因此具有一定的局限性。为了更加精准地刻画病毒在计算机系统中的传播机制,本文将已有的病毒传播模型拓展到分数阶形式,并考虑了隔离期与治愈期两类时滞因素对系统的影响。仅有潜伏期时滞的恶意病毒模型只能反应病毒在计算机内部节点中感染扩散对系统稳定性的影响,而本文提出的另外两类时滞为研究严格的控制措施对恶意病毒在计算机中的传播影响提供了理论分析。

1 模型描述

当计算机被某一类病毒恶意入侵时,病毒会攻击计算机中的各个节点,并且病毒在计算机中的每个节点状态传播时均需要一定的时间。假设计算机中含有易被病毒感染的一些漏洞节点,可称漏洞节点为易感节点;当漏洞节点被病毒攻击后,经过一段时间易感节点转化为感染节点;当用户发现计算机被恶意病毒攻击而采取相应的病毒消杀措施后,感染节点被隔离,转化为隔离节点;感染节点和隔离节点被治愈后转化为恢复节点。

一般的病毒传播模型只考虑了时滞对恶意病毒扩散的影响,没有考虑到病毒的遗传特性,针对这一点可以通过引入分数阶微积分来进一步研究恶意病毒传播模型。分数阶导数有3种常用的定义,即Grunwald-Letnikov定义,Riemann-Liouville定义和Caputo定义[23]。而Caputo分数阶导数在初始条件下与整数阶方程有相同的形式,与其他 分数阶导数相比不需要复杂的Laplace变换式。连续函数f(x)的α阶Caputo分数阶导数表示为

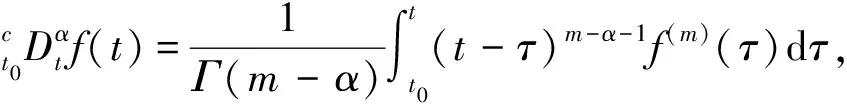
本文提出了如下的Caputo分数阶时滞SIQR(Susceptible-Infectious-Quarantine-Recovered)计算机病毒传播模型

(1)

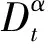
恶意病毒在计算机中传播时的隔离期和治愈期实际为I态节点到Q态节点和Q态节点到R态节点的转化过程,转化过程耗费的时间都基本相似。因此,假设τ1=τ2=τ,模型(1)变为

(2)

2 稳定性和Hopf分岔分析

经计算可得,当β>c1+k+d+μ1时,模型(1)有唯一平衡点E*=(S*,I*,Q*,R*),其中:

令u1(t)=S(t)-S*,u2(t)=I(t)-I*,u3(t)=Q(t)-Q*,u4(t)=R(t)-R*代入模型(2)并进行线性化处理,得到

(3)

模型(3)对应的特征方程为

s4α+A3s3α+A2s2α+A1sα+A0=0

(4)

其中:

A3=a1+a4+a5+a6+b1+b2+b3,

A2=a1a4+a1b1+a1b2-a2a3+a1a5+

a4a5+a5b1+a5b2+a1a6+a4a6+a6b1+

a6b2+a1b3+a4b3+b1b3+b2b3+

a5a6+a6b3,

A1=a1a4a5+a1a5b1+a1a5b2-a2a3a5+

a1a4a6+a1a6b1+a1a6b2-a2a3a6+

a1a4b3+a1b1b3+a1b2b3-a2a3b3+a1a5a6+

a4a5a6+a5a6b1+a5a6b2+a1a6b3+a4a6b3+

a6b1b3+a6b2b3,

A0=a1a4a5a6+a1a5a6b1+a1a5a6b2-

a2a3a5a6+a1a4a6b3+a1a6b1b3+a1a6b2b3-

a2a3a6b3,

并且

a5=d+μ2,a6=d,

b1=ke-sτ,b2=c1e-sτ,b3=c2e-sτ。

选取时滞作为分岔参数,验证模型(2)从稳定到不稳定的Hopf分岔,因此以下讨论无时滞系统的稳定性和有时滞时分岔发生的条件。

2.1 无时滞情形

当τ=0时,此时b1=k,b2=c1,b3=c2,令λ=sα,则特征方程(4)化为

λ4+A3λ3+A2λ2+A1λ+A0=0

(5)

令

Δ1=A3,Δ2=A2A3-A1,

根据劳斯-赫尔维兹判据和分数阶稳定性判据,可以得到以下引理。

引理1 当τ=0时,如果Δi>0(i=1,2,3,4),则方程(5)的所有根都满足|arg (λ)|>απ/2,方程(4)的根都具有负实部。

根据引理1可以得到如下结论。

定理1 当τ=0时,如果Δi>0(i=1,2,3,4),则模型(2)在平衡点E*=(S*,I*,Q*,R*)附近局部渐近稳定。

2.2 有时滞情形

当τ>0时,此时b1=ke-sτ,b2=c1e-sτ,b3=c2e-sτ,则特征方程(4)化为

e-2sτ(B1s2α+B2sα+B3)+e-sτ(C1s3α+C2s2α+C3sα+C4)+(s4α+D1s3α+D2s2α+D3sα+D4)=0

(6)

其中:

B1=c2(k+c1),B2=a6(kc2+c1c2),

B3=a1a6(kc2+c1c2),C1=k+c1+c2,

C2=(a1+a5+a6)(k+c1)+c2(a1+a4+a6),

C3=(a1a5+a1a6+a5a6)(k+c1)+c2(a1a4+

a1b1+a1b2-a2a3+a1a6+a4a6),

C4=a1a5a6(k+c1)+c2(a1a4a6-a2a3a6),

D1=a1+a4+a5+a6,

D2=a1a4-a2a3+a1a5+a4a5+a1a6+

a4a6+a5a6,

D3=a1a4a5-a2a3a5+a1a4a6-a2a3a6+

a1a5a6+a4a5a6,

D4=a1a4a5a6-a2a3a5a6。

式(6)等价于

e-sτ(B1s2α+B2sα+B3)+C1s3α+C2s2α+

C3sα+C4+esτ(s4α+D1s3α+D2s2α+

D3sα+D4)=0

(7)

假设特征方程(7)有一对纯虚根。将s=iω(ω>0)代入方程(7),且替换如下:

e-sτ=e-iτω=cos (τω)-isin (τω),

esτ=eiτω=cos (τω)+isin (τω),

s2α=ω2α(cos (απ)+isin (απ)),

s4α=ω4α[cos (2απ)+isin (2απ)]。

特征方程(7)可化为

[cos (τω)-isin (τω)](F1+iF2)+F3+

iF4+[cos (τω)+isin (τω)](F5+iF6)=0,

其中:

分离上式的虚部实部可以得到方程组

(8)

整理方程组(8)得到

(9)

其中:

T1(ω)=(F5-F1)F3-F4(F2-F6),

T2(ω)=(F1+F5)F4-F3(F2+F6),

T3(ω)=(F2-F6)(F2+F6)F4-

(F5-F1)(F5+F1)。

根据cos2(ωτ)+sin2(ωτ)=1,可以得到

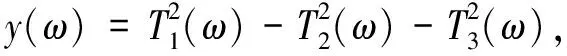
(10)

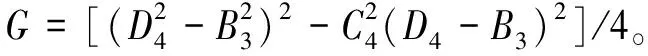
j=0,1,2,…

(11)

定义

给出假设 (H1)G<0。

引理2 当(H1)成立时,方程y(ω)=0至少存在一个正根。

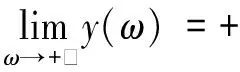
2.3 验证穿越条件

令

Q1(s)=B1s2α+B2sα+B3,

Q2(s)=C1s3α+C2s2α+C3sα+C4,

Q3(s)=s4α+D1s3α+D2s2α+D3sα+D4。

则式(7)可写成如下形式:

e-sτQ1(s)+Q2(s)+esτQ3(s)=0

(12)

方程(12)关于τ求导,可以得到

对上式取倒数可得

令

Q1(s)=P1(ω0)+iP2(ω0),

Q2(s)=P3(ω0)+iP4(ω0),

Q3(s)=P5(ω0)+iP6(ω0)。

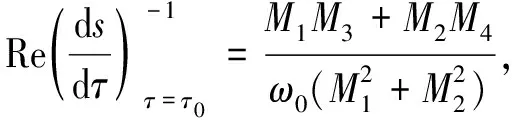
其中:

M1=cos (ω0τ0)(P1(ω0)-P5(ω0))+

sin (ω0τ0)(P2(ω0)+P6(ω0)),

M2=cos (ω0τ0)(P2(ω0)-P6(ω0))-

sin (ω0τ0)(P1(ω0)+P5(ω0)),

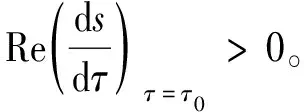
基于上述讨论,可以得到如下定理。

定理2 1)当τ=0时,如果Δi>0(i=1,2,3,4),那么模型(2)在平衡点E*=(S*,I*,Q*,R*)处渐近稳定;

2)如果Gk>0(k=1,2,3,…15)且G<0,那么当τ∈[0,τ0)时,模型(2)在平衡点E*=(S*,I*,Q*,R*)处渐近稳定;

3)当τ>τ0时,模型(2)处于不稳定状态,且当τ穿过τ0时,模型(2)在平衡点E*=(S*,I*,Q*,R*)处产生Hopf分岔,其中τ0是最小的临界点。

3 数值仿真

为验证上述理论分析的正确性,本文使用具体的实例来进行数值仿真。选取参数值A=10,β=0.6,d=0.02,c1=0.08,c2=0.02,k=0.01,μ1=0.03,μ2=0.04,并选取阶次α=0.96。

通过计算可以得到模型(2)的唯一平衡点为E*=(20.833,68.452,8.557,270.366),然后可以验证Δi>0(i=1,2,3,4),模型(2)无时滞时在平衡点E*处渐近稳定。计算可得ω0=0.0848,τ0=26.0947并验证得到假设(H1)符合要求。选择τ=25<τ0,模型(2)在E*处渐近稳定,结果如图1所示;选择τ=30>τ0,模型(2)在E*处不稳定,结果如图2所示。由图1和图2的变化,验证了定理1的正确性。

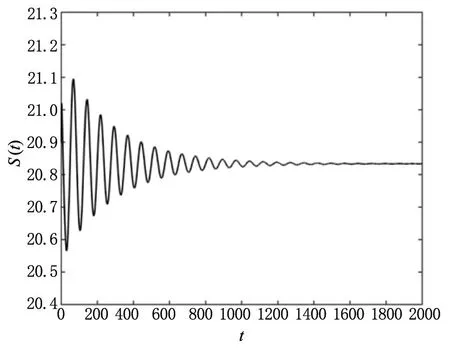
(a)变量S(t)的波形图

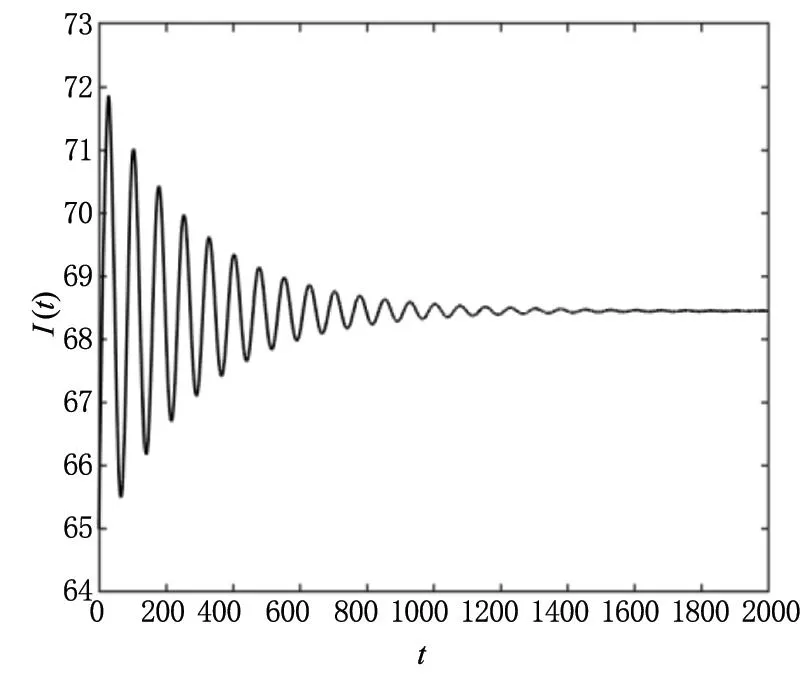
(b)变量I(t)的波形图

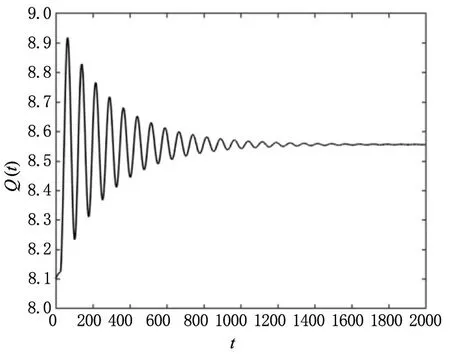
(c)变量Q(t)的波形图

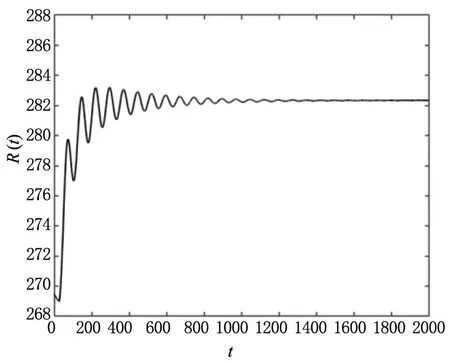
(d)变量R(t)的波形图

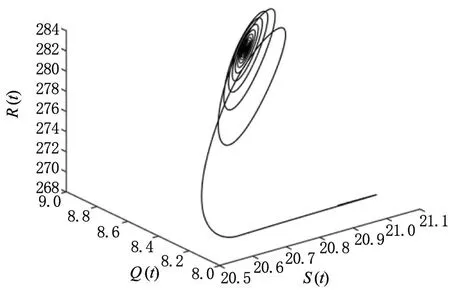
(e)变量S(t),Q(t),R(t)的相图

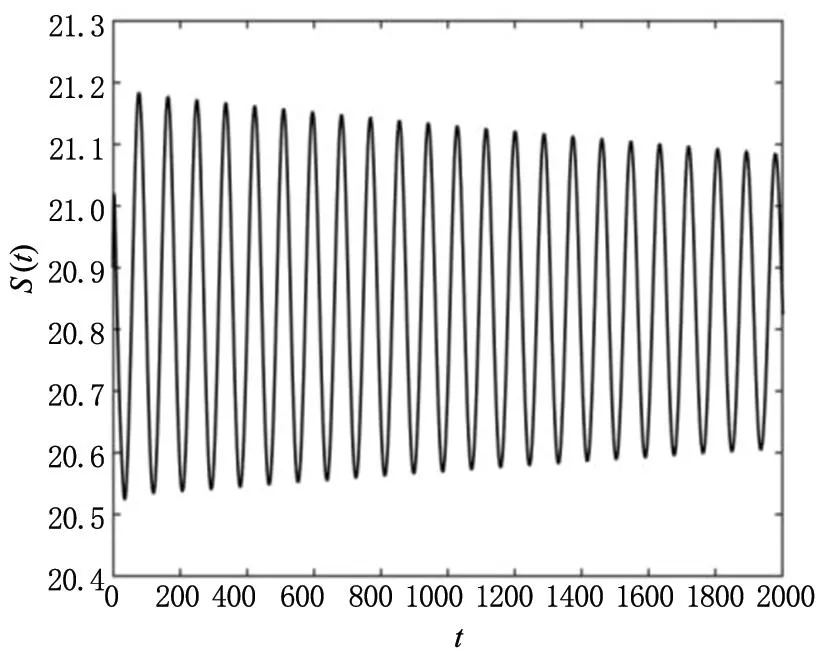
(a)变量S(t)的波形图

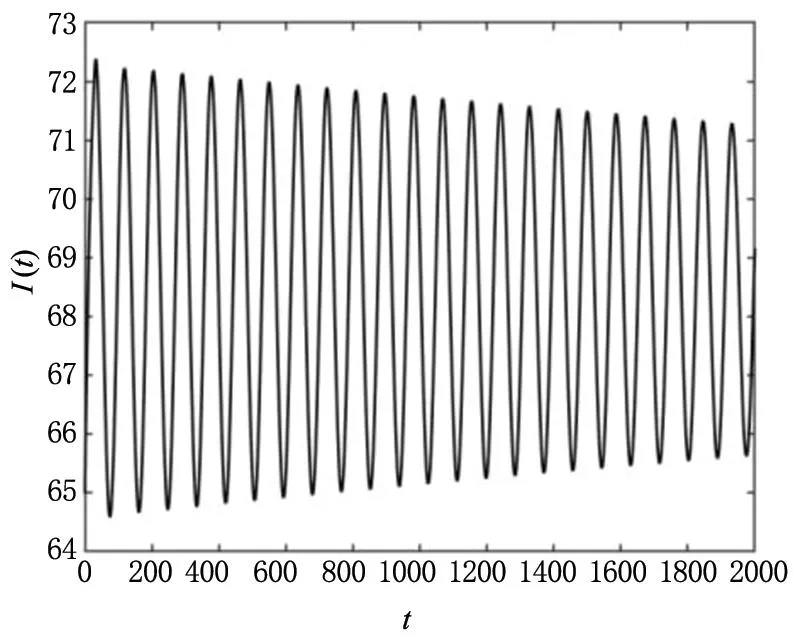
(b)变量I(t)的波形图

(c)变量Q(t)的波形图

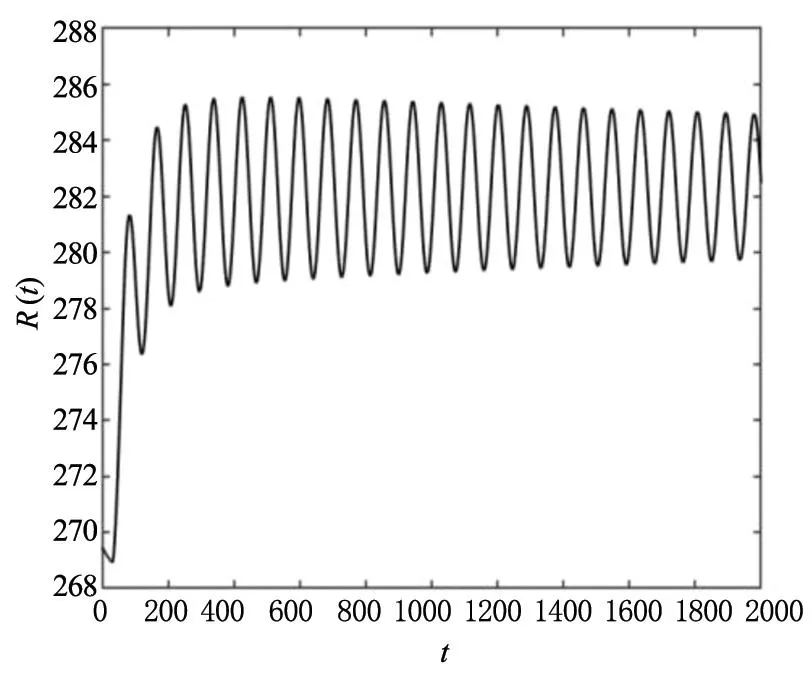
(d)变量R(t)的波形图

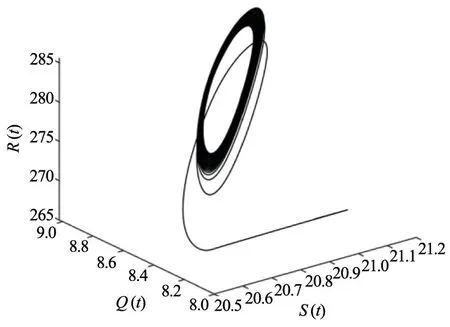
(e)变量S(t),Q(t),R(t)的相图

本文还研究了τ0随α的变化关系。选择不同的α值可以得到相应的τ0的值,如表1所示。

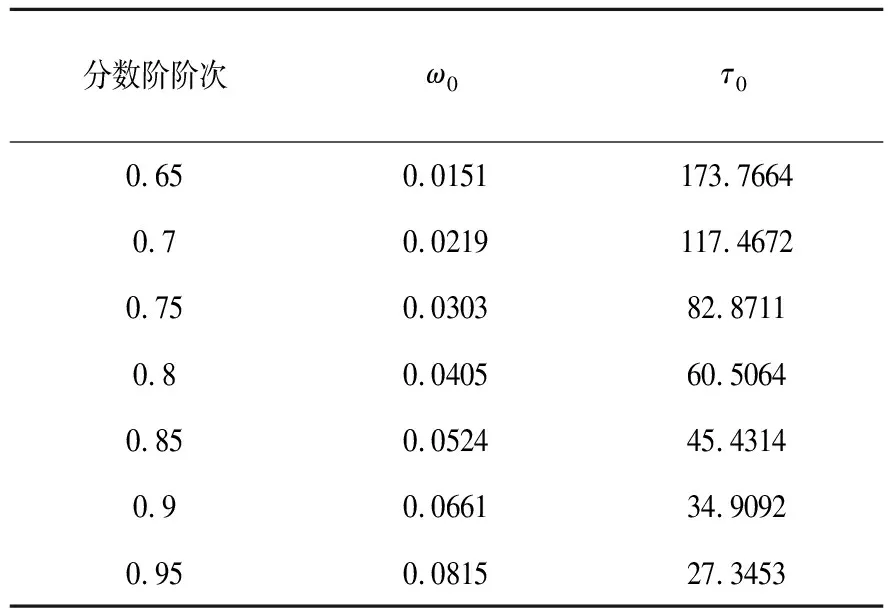
表1 分数阶阶次与穿越频率、分岔时滞的关系

图3给出了分岔时滞τ0随分数阶阶次α的变化曲线。由图3可知,当α∈[0.65,0.75]时,分数阶阶次α越小,穿越频率ω0越小,分岔阈值点τ0越大。

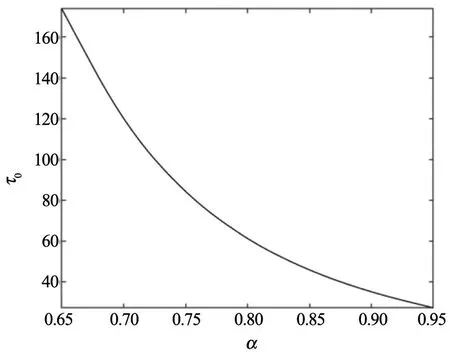
图3 分岔时滞随分数阶阶次变化图

4 结 论

为研究恶意病毒的传播机理,本文提出了一个具有饱和发生率的分数阶时滞SIQR计算机病毒模型,以时滞作为分岔参数,利用导出的特征方程讨论了模型(2)的稳定情况。首先分析了无时滞情形下的稳定性并给出了稳定条件,然后在此基础上研究了有时滞时系统局部稳定和产生Hopf分岔的充分条件。通过理论计算分析表明,当时滞小于分岔阈值时,系统渐近稳定;当时滞穿越分岔阈值时,系统失去稳定性并产生Hopf分岔。最后通过数值仿真来验证理论的有效性和可行性。同时计算得出分岔时滞随分数阶阶次变化的规律,即阶次越小,分岔时滞越大,Hopf分岔现象延后产生。关于SIQR计算机病毒传播模型能否加入扩散项来考虑空间位置对病毒传播机制的影响,我们将在未来的工作中继续研究。