运动抑制装置对圆筒型浮式平台运动响应的影响
2023-12-27李焱黎国彦唐友刚李昊然李耀隆
李焱,黎国彦,唐友刚,李昊然,李耀隆
(天津大学 a.天津市港口与海洋工程重点实验室;b.水利工程仿真与安全国家重点实验室,天津 300350)
能源开发进军深水已成必然趋势[1],深海油气开采后,经加工处理后储存于水面浮体,因此需要应用浮式生产装置(FPSO)等水面装备进行。传统FPSO通常由油船改装而成,细长的船型使得浮体受到的横向载荷远大于纵向载荷。由于南海海域海况相对恶劣,为防止风浪载荷过大引发结构破坏,故通常采用具有风标效应但造价相对较高的单点系泊系统进行定位,投资成本上升的同时,单点处的运动往往达到数十米。为此,国内外学者提出了多种新型FPSO以解决这一问题。其中圆筒形FPSO由于圆形的对称性,浮体对于波浪入射方向并不敏感,横摇、纵摇、艏摇运动性能相比船型FPSO大幅提高,故可以采用多点系泊系统,降低设计建造成本。尽管如此,圆筒型FPSO垂荡运动过大,仍难以满足干式采油树的应用条件。
为了弥补这一短板,国内外学者开展了一系列研究[2-5],有研究者提出在主筒体的下方增加延伸筒体,并在延伸筒体周围环向布置1套箱型结构作为结构,提升浮体运动阻尼以抑制圆筒形FPSO的垂荡运动,数值分析与模型试验初步验证了该方案加装干式采油装置的可行性[6]。为此,考虑以该方案为原型,选取高度、宽度、截面形状、通海情况等为分析对象,基于三维势流理论计算波浪作用下圆筒形FPSO的稳态运动响应幅值,以探索不同参数对浮体运动性能的影响。
1 圆筒形FPSO及其运动抑制装置
以圆筒形FPSO为母型,结合我国南海海域典型风浪环境及油气储量等条件,提出一种储量为60 000 m3的圆筒形FPSO,其主尺度见表1,剖面见图1。

图1 带运动抑制装置的圆筒形FPSO

表1 圆筒型FPSO主要参数 m
在主筒体下方布设直径相同的延伸筒体,其底部开设孔隙。在延伸筒体外设置矩形截面的环形阻尼结构,环向等间距布置8个连接件,保证阻尼结构与FPSO筒体之间牢固连接的同时,阻尼结构与延伸筒体间形成间隙水道,增大浮体的湿表面面积从而有效增大浮体黏性阻尼。阻尼结构上同样开设孔隙,延伸筒体与阻尼结构共同组成圆筒形FPSO的运动抑制装置。圆筒形FPSO中部开有圆形月池,并向下贯通延伸筒体,保证生产立管可以直通上部生产甲板,其中延伸筒体内月池形状为圆台形,防止立管与延伸筒体发生碰撞。主筒体内设有货油舱与压载舱,动态调节货油及压载水的质量,保证两者总重量不变,实现不同工况下圆筒形FPSO吃水保持不变。通过这样的设计,可以保证运动抑制装置内的水体与外界海水连通,使结构内外静水压抵消,既不额外增加FPSO的排水量,又可以提升结构附连水质量,延长FPSO的垂荡固有周期以避开波浪卓越周期。另一方面,运动抑制装置内外水体可以通过开孔自由流动,增加结构所受流体阻尼,起到抑制FPSO垂荡运动的效果。
2 水动力计算理论与计算模型
采用三维势流理论预报FPSO在不同波浪条件下所受的波浪载荷及稳态运动响应。三维势流理论基于以下假设:①流体均匀的、不可压缩的;②忽略流体的粘性,认为流体的运动无旋。在此前提下,流域内各点具有速度势,并且满足拉普拉斯方程。
(1)
由线性势流理论可得,流场的总速度势可以分解为入射势、绕射势和辐射势3个部分。
Φ(x,y,z,t)=ΦI(x,y,z,t)+
ΦD(x,y,z,t)+ΦR(x,y,z,t)
(2)
式中:入射势表示入射波对结构的作用,求解入射势时通常采用Airy波理论,假设流体为势流,且波浪为微幅波,波浪中的流体质点以固定的圆频率做圆周运动。根据流体的边界条件以及控制方程,可以得出微幅波下的入射波速度势的表达式。
(3)
式中:η为波面升高函数;k为波数;d为水深;ω为波浪圆频率。而射速度势的求解不仅要满足入射速度势的边界条件,还需要物体湿表面满足于入射速度势相关的反射条件。浮体漂浮时会自由运动会扰动湿表面附近流体产生辐射速度势,依据辐射势的成分,一般分为附加质量akj和阻尼系数bkj,由下式进行计算。
akj=-Re(ρ∬S0ΦjnkdS0)
(4)
bkj=-Im(ρω∬S0ΦjnkdS0)
(5)
根据平台主尺度参数,建立圆筒形FPSO的面元模型见图2。

图2 圆筒形FPSO的水动力分析面元模型
基于以上计算公式在频域内计算圆筒形FPSO水动力性能。在一定时长的波浪作用下,浮体可以达到稳定的运动状态,采用频域方法求解浮体稳态运动,假设浮体为刚体,根据牛顿第二定理建立运动方程。
[-ω2(M+Ma(ω))+iω(B(ω)p)+
Bn+C+Ce]X(ω,β)=F(ω,β)
(6)
式中:M为质量矩阵;ω为入射波圆频率;β为浪向角;Ma(ω)为附加质量矩阵;B(ω)p为辐射阻尼矩阵;Bv为黏性阻尼矩阵;C和Ce分别为静水与系泊系统回复力矩阵;X(ω,β)为一阶频域运动响应矩阵;F(ω,β)为一阶波浪激励力。
采用挪威船级社水动力计算软件SESAM进行建模计算,结合浮体与海水的实际接触情况,按照1∶1的比例建立圆筒形FPSO及其运动抑制装置的湿表面面元模型。透明水平面为静水面,水面以下为湿表面面元,上部为主筒体的干舷部分。依据运动抑制装置设计方案,在对应位置建立阻尼孔的同时,对延伸筒体与阻尼结构内外表面均赋湿表面属性,以保障两者内部水体与外部海水实现连通。此外筒体上部还有生产甲板与上部组块等结构,但由于该结构未接触海水,故对水动力计算无影响,在建模中予以简化。由于SESAM软件基于势流理论,无法考虑黏性阻尼的影响,因此采用人工添加阻尼的方式估算阻尼孔及运动抑制装置的附加阻尼,阻尼系数参考之前开展的CFD与模型试验结果,取8%。
3 运动抑制装置的影响
建立采用不同阻尼结构的圆筒形FPSO模型,分析阻尼结构的高度、宽度、截面形状、通海情况对圆筒形FPSO水动力性能的影响。采用三维势流理论计算浮体所受水动力载荷,并在频域内对其动力响应特性进行预报。在2~40 s的入射波浪范围内,计算平台一阶波浪力、二阶漂移力、附加质量、势流阻尼等波浪载荷,并基于频域运动控制方程计算平台各自由度的运动RAOs。
3.1 运动抑制装置通海情况的影响分析
通过在舱室上下表面加开通海孔,使海水可以自由流入阻尼结构与延伸筒体。为此,以阻尼结构的通海情况为变量,针对阻尼结构和延伸筒体是否通海,建立通海情况为全部通海、全部封闭两种模型(通海情况示意图见图3),其他变量控制相同:阻尼结构高度为10 m、宽度为10 m,采用四边形截面形状。不同阻尼结构通海情况下圆筒形FPSO垂荡、纵荡及纵摇运动RAO及峰值对应周期附近的加密计算结果见图4。
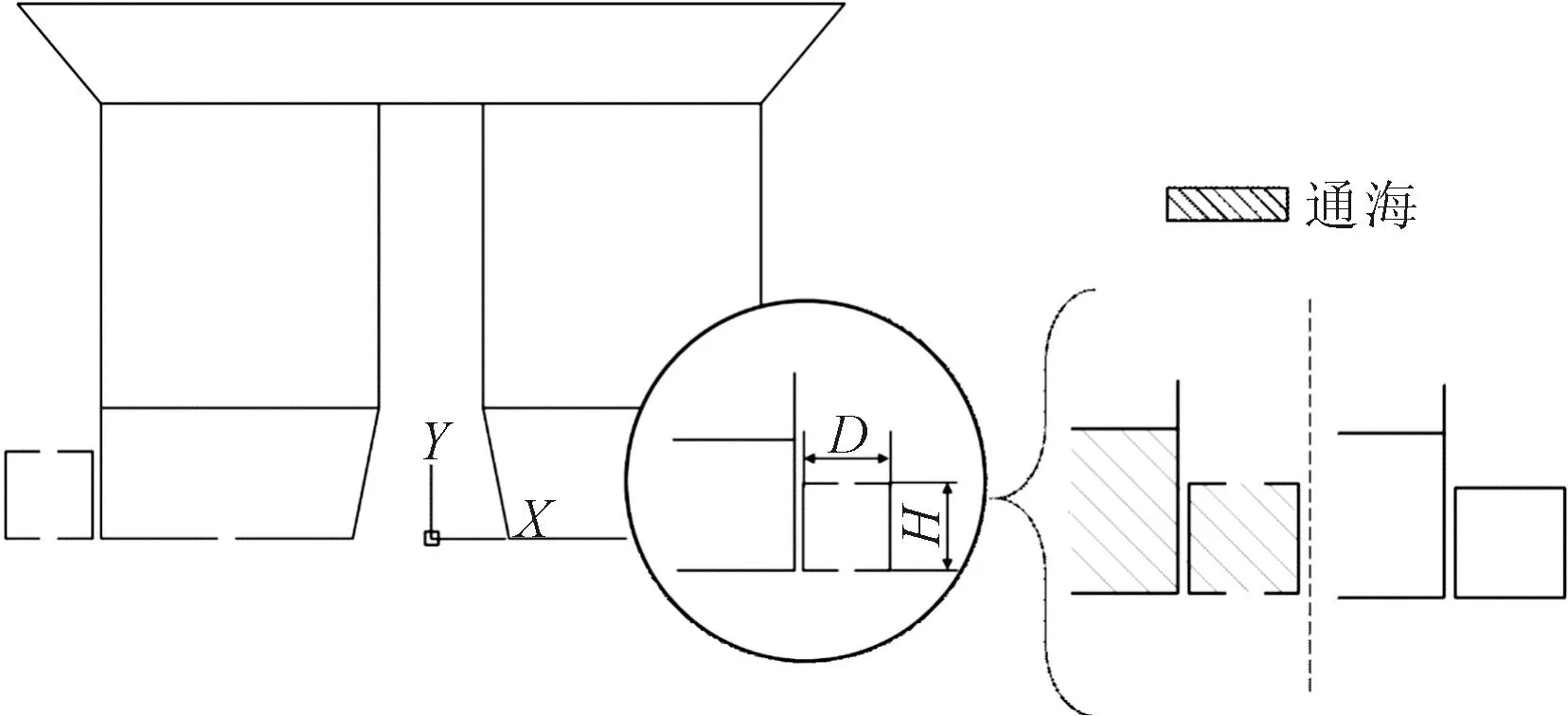
图3 阻尼结构通海情况示意

图4 不同阻尼结构通海情况下圆筒形FPSO的运动响应
由图4a)、b)可见,阻尼结构与延伸筒体均通海时,浮体垂荡运动RAO幅值明显小于两者均封闭时的幅值,但垂荡峰值对应的固有周期略有降低。由图4c)、d)可以看出,运动抑制装置通海将导致纵荡运动幅值略有增加。由图4e)、f)可见,运动抑制装置通海后使纵摇运动的幅值增大,同时运动的固有周期略有增加。综上,从对于TTR立管安全性影响最主要的浮体垂荡运动角度来说,在延伸筒体和阻尼结构开设阻尼孔通海,有利于浮体垂荡运动性能的优化。
3.2 阻尼结构高度的影响分析
采用矩形截面的阻尼结构,取宽度为10 m,分别建立阻尼结构高度(见图3中H)为11、12、13、14、15 m五种模型,延伸筒体和阻尼结构均可通海。不同阻尼结构高度条件下圆筒形FPSO垂荡、纵荡及纵摇运动RAO见图5。在各自由度运动达到峰值对应波浪周期处,对波浪圆频率进行加密,计算并绘制RAO峰值附近的放大曲线图。

图5 不同阻尼结构高度下圆筒型FPSO的运动响应
由图5a)、b)可见,当FPSO的阻尼结构高度落在11~15 m的区间时,随阻尼结构的高度增加,圆筒FPSO垂荡运动RAO峰值下降,固有周期则呈现逐步增大的趋势。从图5c)、d)可见,随阻尼结构高度增加,圆筒FPSO纵荡运动RAO最大值呈现下降趋势,且峰值对应周期也逐渐增大。从图5e)、f)可见,圆筒FPSO纵摇运动的幅值亦随着阻尼结构高度增大而下降,但峰值对应的固有周期变化并不显著。综上,增大阻尼结构的高度有利于FPSO运动性能的优化,且从幅值变化上来看,相比于垂荡和纵荡,纵摇对阻尼结构的高度变化更加敏感。其原因在于阻尼结构高度的增加可以有效增大浮体系统的运动附连水质量,从而增大运动固有周期。
3.3 阻尼结构宽度的影响分析
采用矩形截面的阻尼结构,取高度为10 m,以阻尼结构的宽度为变量,建立5种模型,宽度(见图3中D)分别为11、12、13、14、15 m,延伸筒体和阻尼结构均可通海。不同阻尼结构宽度条件下圆筒形FPSO垂荡、纵荡及纵摇运动RAO,以及峰值对应周期附近加密计算结果见图6。

图6 不同阻尼结构宽度下圆筒型FPSO的运动响应
由图6a)、b)可见,当FPSO的阻尼结构宽度落在11~15 m的区间时,浮体垂荡运动RAO曲线有2处峰值,其中第一个峰值全部落在波浪的卓越周期内,但数值相对较小,第二个峰值对应波浪周期高于18 s,但运动响应相对较大。波浪周期在2~12.5 s内,阻尼结构的宽度增加,垂荡RAO增大,峰值对应周期几乎不变;波浪周期大于15 s的时候,阻尼结构宽度越大,垂荡越小;在第二个波峰附近,宽度增加,峰值几乎相同,峰值对应的固有周期整体上呈现增加的趋势。从图6c)、d)可见,随阻尼结构宽度增加,圆筒型FPSO纵荡运动最大值呈现下降趋势,且峰值对应的固有周期也逐渐增大。而从图6e)、f)可见,纵摇运动RAO曲线有两处峰值,其中第一个峰值全部落在波浪的卓越周期内,但数值相对较小,第二个峰值对应波浪周期高于24 s,但运动响应相对较大。波浪周期在9~15 s内,阻尼结构的宽度增加,纵摇RAO的增大,峰值对应周期增大;波浪周期大于20 s的时候,阻尼结构宽度增加,纵摇RAO减小,峰值对应的固有周期增大。
综上,增大阻尼结构的宽度有利于FPSO运动性能的优化,与增大阻尼结构高度的原理相似,本质上都增大了浮体运动时的附连水质量,使运动固有周期增大。
4 结论
1)延伸筒体和阻尼结构通海有利于优化浮体垂荡运动性能,但运动抑制装置通海在一定程度上会放大纵荡和纵摇RAO峰值。以垂荡运动性能为主要考虑因素,运动抑制装置的延伸筒体和阻尼结构通海有利于干式采油装备的应用。
2)在一定范围内增加阻尼结构的高度和宽度,均可以使垂荡运动幅值降低,优化浮体运动性能,其中宽度的影响更为显著。同时,增大阻尼结构的宽度对于增加浮体各自由度运动的固有周期起到显著的正面效果,使得浮体运动可以远离波浪周期,避免共振。
3)在后续研究中考虑采用BP神经网络等智能算法对运动阻尼的尺度进行深度优化,以确定使浮体运动性能最优的阻尼结构设计参数;此外还可以采用计算流体动力学方法考虑流体粘性导致的阻尼,更加精确地预报圆筒型浮式平台在波浪作用下的运动响应。
