某露天矿山预裂爆破参数优选与试验研究
2023-12-26陈啸林张智宇孟佳乐
陈啸林,张智宇,王 凯,孟佳乐,彭 磊,吴 霄
(1.昆明理工大学国土资源工程学院, 云南 昆明 650093;2.昆明理工大学公共安全与应急管理学院, 云南 昆明 650093;3.浙江省隧道工程集团有限公司, 浙江 杭州 310000)
预裂爆破是指在开挖主爆区前,为缓冲和反射爆破所形成的冲击波,先沿设计轮廓爆出一条贯穿裂缝,降低爆破对周边岩体的振动破坏,从而获得较平整的开挖剖面[1]。在预裂爆破技术应用中,设置合适的预裂孔参数至关重要[2],国内外相关领域的专家学者对此开展了深入研究。例如,Bendezu 等[3]提出了一种基于有限元方法的数值方法来模拟爆炸裂纹的传播过程。王和平等[4]以大孤山铁矿作为研究背景,模拟了该矿山的预裂爆破过程,从模拟结果中获取了相关爆破参数。杨仁树等[5]为分析爆破裂纹的动态断裂特性,应用数字激光动态焦散技术,获得了相关规律性数据。朱必勇等[6]为了取得较好的预裂效果,设计了多种方案对预裂孔参数进行模拟,结果表明:围岩的破坏程度随着不耦合系数的增加而降低,孔间距的变化对爆破破坏范围影响不大,但大孔距无法形成贯穿的预裂缝。Ma 等[7]基于理论研究,确定了预裂爆破相关参数,并在某边坡进行了常规预裂爆破和精确延时逐孔起爆预裂爆破现场试验,结果表明:常规同排爆破振速的平均降低率为26.40%,逐孔爆破振速的平均降低率为41.45%,半孔率达80.70%。叶海旺等[8]以白鹤滩水电站作为研究对象,通过数值模拟结合现场试验,探究孔间延期时间、孔距等参数与预裂成缝之间的关联性,从而获得了最佳延期时间和预裂孔孔距。Zhang 等[9]采用数值模拟软件分析了预裂爆破相关参数对预裂爆破效果的影响,并将模拟结果应用于具体的施工过程,得到了良好的预裂效果,直接验证了应用预裂爆破技术的有效性。宫嘉辰等[10]在试验中以砂岩作为模拟对象,通过分析隧道爆破力学模型试验结果,找到了相似材料成分数据,基于正交试验法,得到了相似材料的基本力学性质参数。单仁亮等[11]基于相似理论,通过模型试验验证其在实践中的应用,以期为准直眼掏槽爆破技术施工现场提供借鉴。
不耦合系数是预裂爆破的重要参数,在许多情况下都采取不耦合装药形式,从而有效地降低炸药爆炸过程中的冲击力。孔距对预裂爆破效果的影响很大,同样是孔网参数中至关重要的参数[12]。在工程爆破施工中,毫秒延期爆破技术的应用范围较广,计算并优化起爆微差时间是目前国内外众多学者面临的一个难题。若选取的起爆微差时间较小,则不能有效地将炸药能量分散开来,预裂效果不理想;若微差时间太大,则等同于单孔的分次起爆过程,而单孔起爆间隔时间过长很可能会对爆破网路造成一定程度的损坏,不利于破岩工作[13]。因此,合理选择爆破参数,可以有效地改善预裂效果,保障周边岩体和建筑物的安全性。数值仿真技术作为重要的辅助研究方法之一,被广泛地应用于边坡处理等实际工程中。本研究首先对裂纹扩展在数值模拟以及物理模型试验中的研究现状和研究成果做简要回顾,在此基础上,通过数值模拟、相似材料选择、相似试验设计,优选出最佳预裂孔参数组合,基于现场获取的相关参数,选用相应的本构,利用三维动力分析软件LS-DYNА 分析爆破参数与裂纹扩展之间的演变规律,为优化爆破工艺和实际应用提供理论依据。
1 工程背景
以云南某矿山为例,采场最低开采标高为910 m,最高标高为1 340 m,边坡最大高度为430 m。矿岩主要为片岩、矽卡岩、大理岩岩种,其中:片岩节理发育程度较高,岩石完整性较差;矽卡岩裂隙发育,岩层完整性差;大理岩节理、裂隙发育,岩层为层状、似层状、透镜状。因长期受地质作用的影响,岩体发生较严重的风化现象,边坡上段大部分为较厚的全-强风化层,下段以中等风化岩体为主,同时受降雨、地下水等因素的影响,边坡稳定性及安全问题日益严峻。爆破作为矿山开采的主要手段,开采过程中应充分考虑边坡稳定性,并尽可能地减少其对现场作业的负面影响。因此,采用预裂爆破不仅可以减少边界超挖和欠挖现象,而且可以保证断面的平整,减小爆破振动对边坡的不良影响,保障边坡的稳定性。为此,在初步掌握预裂爆破致裂机理的基础上,通过数值模拟结合模型试验确定合理的爆破参数,以期实现爆破效果的精确控制,促进预裂爆破在矿山开采中的应用。
2 数值模拟方法
以矿山某区域大理岩为爆破对象,分析不同爆破参数下的裂纹扩展规律,为现场预裂孔参数设计提供参考依据。
2.1 材料模型及其参数
2.1.1 大理岩
大理岩采用线性状态方程描述,表达式[14]为
式中:p为压力,GPa;K为体积模量,GPa;ρ/ρ0为比容,ρ 为当前密度,ρ0为初始密度。
采用RHT(Riedel-Hiermaier-Thoma)模型描述岩石本构时,应考虑应力对损伤面形状的影响,其中主要考虑应力张量第三不变量。p-α 状态方程见图1(a),其中:α 为孔隙度,pcrush为孔隙压碎压力,pcomp为压实压力。当压力低于pcrush时,岩石近似为弹性材料;当压力继续增大直至多孔材料被完全压实,岩石发生塑性变化。对于给定的应力状态和加载速率,只有当载荷超过材料的屈服极限时,材料才发生屈服。在模型中嵌入相关的压力方程,以便准确、高效、等量地模拟实际工况。这些方程主要用于描述冲击荷载下岩石的初始屈服强度、失效强度和残余强度的变化规律,如图1(b)所示,其中:σ 为应力,D为损伤变量,εp为线性强化段累积等效塑性应变,具体表达式见文献[15-16]。利用εp定义损伤变量
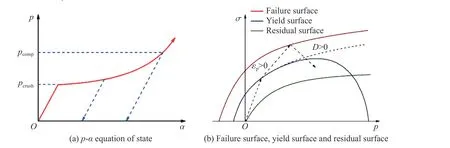
图1 RHT 模型Fig.1 RHT model
式中:D为损伤变量,为破坏时的等效塑性应变。
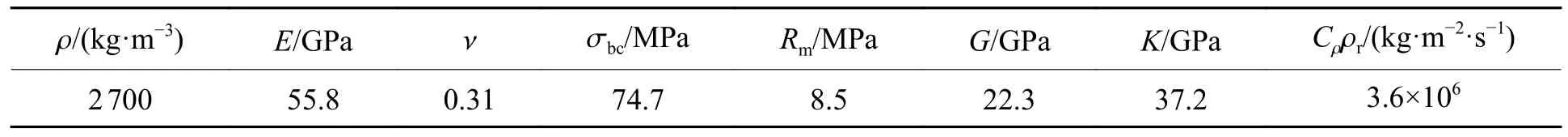
表1 大理岩参数Table 1 Marble parameters

表2 岩石RHT 模型参数Table 2 Rock RHT model parameters
2.1.2 炸 药
炸药选用1 号岩石乳化炸药,采用JWL 状态方程[17]描述,即
式中:E0为单位体积炸药的内能,V为相对体积,Ae、Be、R1、R2、ω 为材料常数。炸药材料及其JWL 状态方程参数取值见表3,其中ρb为炸药密度,Cd为炸药爆速。

表3 炸药材料及JWL 状态方程参数Table 3 Explosive material and the JWL equation of state parameters
2.1.3 空 气
建立不耦合装药数值模型时,药卷四周有一层气体,模拟时可用其他关键词替代,如*MАT_NULL,建模结束后,将其参数改变为相应的气体物料,其LINEАR-POLYNOMIАL状态方程为
式中:μ为体积比,一般情况下,μ=1.4;C0~C6为实常量,C0=C1=C2=C3=C6=0,C4=C5=0.4;Ea为单位体积空气的内能。
2.2 数值模型的建立
如图2 所示,模型尺寸(长×宽×厚)为500 cm×400 cm×1 cm,分别对应x、y、z轴;炮孔沿中心水平轴线布置,以x=250 cm 为对称轴,炮孔直径为9 cm。利用LS-DYNА 进行前处理建模,采用映射方法划分模型。模型四周设置非反射边界,以模拟无限域岩石。
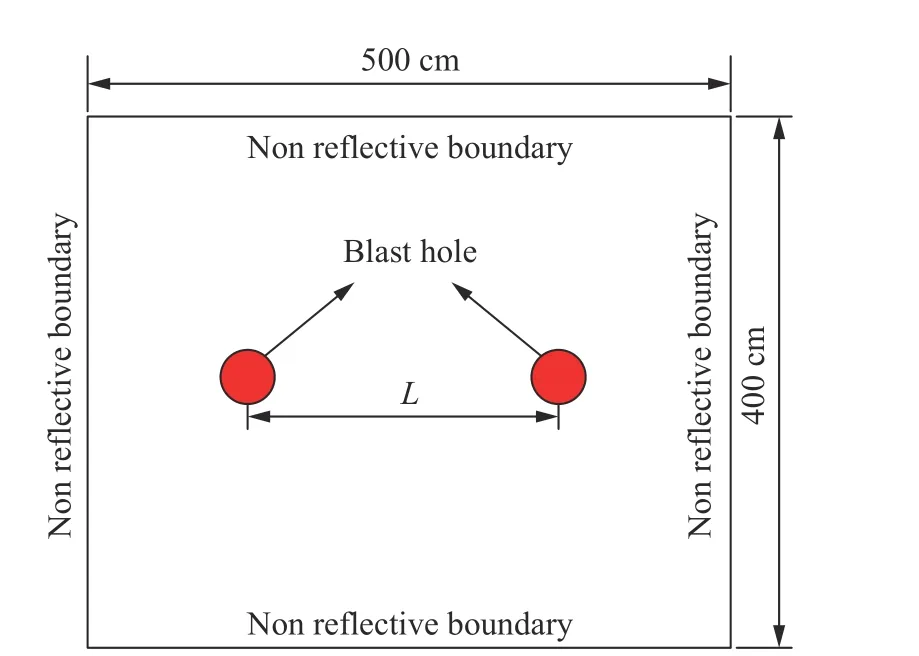
图2 有限元模型Fig.2 Finite element model
根据有关资料[18],中硬以上岩体预裂孔间距L取8d~12d(d为孔径),因此本研究中L取72、81、90、99 和108 cm。徐颖等[19]的模型试验结果表明,当不耦合系数k为1.67 时,裂纹数及裂纹延伸长度达到最优,因此本研究中不耦合系数取1.33、1.67、2.00、3.00。何理等[20]采用混凝土模型开展了预裂爆破试验,结果表明,孔间延期时间(Δt)的最优取值为11~15 ms;司剑峰等[21]基于相似原理,根据模型试验结果,确定钻孔爆破孔间最佳延期时间为8 ms。综合以上研究,选取0、8、10、12、15 ms 作为本次模拟试验的延期时间。
3 数值模拟分析
3.1 双孔同时起爆
模拟了不同孔距和不耦合系数条件下预裂爆破裂纹扩展情况,结果如图3 所示。从模拟结果可以观察到,采用较小的不耦合系数时,两孔连线中心处形成了叠加效应,同时在爆破孔附近,裂纹存在明显的分叉现象且范围较大,即对岩体造成的破坏较大。随着孔距增大,裂纹仅在局部连通,而非贯穿炮孔,说明预裂效果较差。

图3 不同工况下的裂纹扩展结果Fig.3 Crack extension results under different working conditions
3.1.1 最佳爆破孔孔距
通常可以用有效应力表征岩石的应力特征。当有效应力达到岩石的动态抗拉强度屈服极限时,岩石发生破坏。绘制了最大拉应力与孔距的关系曲线,以分析其演变规律,确定最佳孔距。
图4 为双孔连线中点处最大拉应力随孔距的变化曲线。可以看出,随着孔距增大,岩石双孔连线中点处的最大拉应力降低。一般认为,岩石动态抗拉强度是其静态抗拉强度的3 倍[22]。岩石的静态抗拉强度Rm为8.5 MPa,由此计算得到其动态抗拉强度为25.5 MPa。当孔距大于90 cm、不耦合系数为3.00 时,双孔连线中点处的最大拉应力低于其动态抗拉强度,说明岩石不能形成完整的预裂缝。

图4 双孔连线中点处最大拉应力随孔距的变化曲线Fig.4 Change curves of the maximum tensile stress at the midpoint of double hole line
综上分析,在保证预裂爆破效果的前提下,应尽可能地减少钻孔数量(即增大孔距),保证岩体周围不产生较大破坏,因此孔距的最优取值为81 cm,即孔距与孔径之比(L/d)为9。
3.1.2 最佳不耦合系数
当L取81 cm(L/d=9)时,4 种不耦合系数下的孔壁压力(pg)时程曲线如图5 所示。由图5 可知,k不同时,孔壁承受的压力亦不同。其中:k=1.33 时,爆破冲击载荷产生的孔壁压力最大,达到压力峰值1 270 MPa;当k=1.67 时,爆破冲击载荷产生的压力为621 MPa,由于爆破冲击载荷已经减弱,所以压力开始衰减;当k=2.00 时,随着爆破冲击载荷的持续减弱,产生的压力降低至395 MPa;在k=3.00 时,孔壁压力峰值已降至271 MPa,相比最大峰值,降低了78.7%,此时爆破损伤程度较小,有效地保护了炮孔壁。分析其原因:在爆破过程中,药卷周围空气对冲击波的冲击载荷具有很好的缓冲效果,能有效地降低爆破过程中炮孔壁的压力峰值。

图5 L=81 cm 时不同不耦合系数条件下的孔壁压力时程曲线Fig.5 Time-history curves of the hole wall pressure under different decoupling coefficients at L=81 cm
当L取81 cm(L/d=9)时,粉碎区半径随k的变化曲线如图6 所示。随着k增大,粉碎区半径呈下降趋势,说明粉碎区的破坏程度降低。实际工程中,不仅要满足炮孔裂隙贯通要求,而且在炮孔周围不能产生大范围破坏,即叠加应力小,同时炮孔附近裂隙扩展对岩体的危害是可控的,从而保证围岩的安全和稳定。综合图5 和图6 的分析结果,从孔壁内部不过度粉碎的观点出发,k的最优值为3.00。
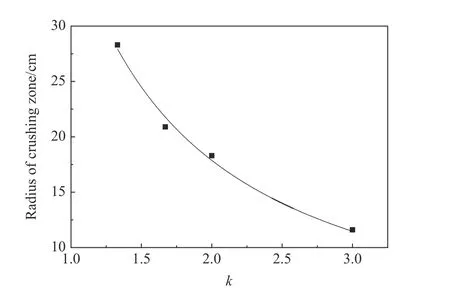
图6 L=81 cm 时粉碎区半径随不耦合系数的变化曲线Fig.6 Change curve of the radius of the crushing zone with decoupling coefficient at L=81 cm
3.2 最佳起爆延期时间
设L=81 cm(L/d=9),k=3.00,进行岩石双孔爆破模型模拟试验,先爆孔(左侧炮孔)与后爆孔(右侧炮孔)的起爆延期时间设为0、8、10、12、15 ms,求解时间设为0.02 s,裂纹扩展最终结果见图7。

图7 裂纹扩展结果Fig.7 Crack extension results
图8 为所选单元示意图。共选取8 个单元,其中:单元А、B、C、D、E 等距离分布在双孔连线上,单元А 靠近左侧炮孔,单元B 位于中间偏左处,单元C 位于两孔连线中点,单元D 位于中间偏右处,单元E 靠近右侧炮孔,单元F 位于左侧炮孔上方,单元G 位于双孔连线中点上方,单元H 位于右侧炮孔上方。

图8 单元示意图Fig.8 Schematic diagram of the unit
图9 显示了炸药起爆后А、B、C、D、E 5 个单元承受的有效应力时程曲线。单元А 和单元E 在0.03 ms 最先出现有效应力,然后是单元B 和单元D(0.05 ms),最后是单元C(0.08 ms)。这是由于爆破产生的应力波先传递至单元А 和单元E 处,再传递至单元B 和单元D 处,最后到单元C。有效应力峰值由大到小依次为单元А(65.6 MPa)、单元E(65.0 MPa)、单元C(57.0 MPa)、单元B(48.2 MPa)、单元D(46.5 MPa)。尽管单元C 距离两炮孔最远,但是由于爆炸应力波传递至单元C 时产生了应力叠加现象,使得单元C 的有效应力有了一定的增幅。当应力波逐渐消失时,各单元的有效应力振荡降低,由此进一步证明裂纹先由炮孔壁产生,炮孔附近的原岩受到的破坏程度较大。
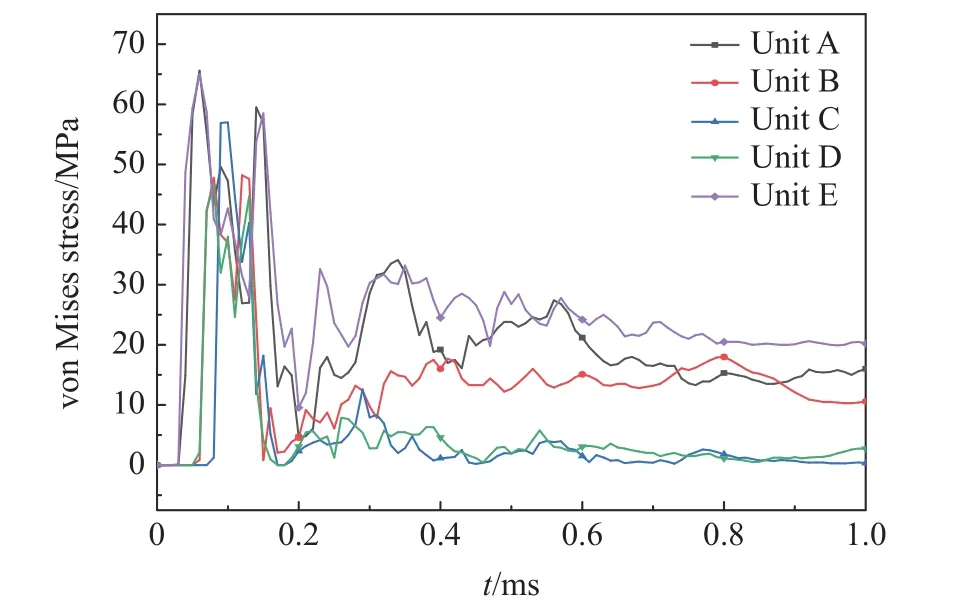
图9 同时起爆时5 个单元的有效应力变化曲线Fig.9 von Mises stress variation curves of five units during simultaneous detonation
记录延期时间之后各单元的最大拉应力,如图10 和图11 所示。

图10 破坏岩体单元最大拉应力随延期时间的变化Fig.10 Variations of the maximum tensile stress of the failure rock mass unit with the delay time

图11 保留岩体单元最大拉应力随延期时间的变化Fig.11 Variations of the maximum tensile stress of retaining rock mass unit with delay time
图10 显示了双孔连线上单元(破坏岩体单元)的最大拉应力随延期时间的变化。其中,左侧炮孔附近的单元А 受到的冲击力影响最大,起爆时产生的应力峰值最大,可达65.6 MPa,意味着爆破过程中对周围岩体造成较大破坏。右侧炮孔附近的单元E 的应力峰值在延期时间为12 ms 时达到最大值,表明此时应力叠加耦合度较高,能量损失较少。单元C 的应力峰值为42.3 MPa,较同时爆炸过程中的应力峰值减小25.8%,大幅降低附近岩体的损伤。随着延期时间增加至15 ms 时,单元最大拉应力呈降低趋势,表明延期时间过长会降低应力,先爆孔产生的冲击波在孔壁上形成应力,且随着时间的增加而衰减,当后爆孔产生的冲击波在孔壁上形成应力时,先爆孔所产生的应力波几乎完全消失,应力叠加效应减弱,应力减小。
图11 显示了保留岩体单元的最大拉应力随延期时间的变化。同时起爆时,保留岩体处的最大拉应力大于岩石的动态抗拉强度,岩体发生一定程度的破坏。与其他3 个延期时间相比,延期时间为12 ms 时,保留岩体单元的最大拉应力均小于岩石的动态抗拉强度,起到了保护周边岩体的作用。
综上所述,为达到预裂成缝的效果,同时保证周边岩体不受破坏,从模拟试验结果可以看出,延期时间取12 ms 时效果最佳。
4 相似模型试验
通过模型试验可以精确地得到试件爆后形态,从而直观地测出半孔率和预裂缝宽度,以评判预裂效果[23]。为验证数值模拟结果,开展了模型试验,从而确定最佳预裂孔参数组合。
4.1 试件的制备
根据相似准则,选择C30 混凝土作为相似材料,其中水、水泥、砂、石子的配比为0.60∶1.00∶2.51∶3.93。模型材料的各项指标如表4 所示,其中:ρm为模型试件密度,σm为模型试件的抗压强度,Em为模型试件的弹性模量。在本试验中,试件为长方体的箱体,尺寸(长×宽×高)为50 cm×50 cm×90 cm。将水泥灌满模具后,约10 min 后水泥强度达到一定程度,此时在混凝土中插入钢筋预留炮孔。为研究最大单响药量的影响,根据模型尺寸,取炮孔数量为4,半孔率及预裂缝宽度取其平均值。第1 天间隔30 min 转动一次钢筋,接下来的7 d 内每天旋转一次,避免钢筋在水泥中凝固而无法拔出,在28 d 内每日为其浇水一次,模型试件如图12 所示。

表4 模型材料指标Table 4 Model material indicators

图12 模型试件Fig.12 Model specimen
4.2 模型试验的相似性和相似系数
以相似原理为依据,可以将模型的相似性概括为材料相似、几何相似和爆破动力相似[11]。因此,从这3 个方面分析此次试验,确定其相似性和相似系数。
4.2.1 材料相似
材料相似应考虑材料密度、应力、弹性模量、介质波阻抗、泊松比、应变、内摩擦角、静摩擦系数等参数,根据量纲分析法,模型试验中无量纲的物理量包括泊松比、应变、内摩擦角、静摩擦系数等,无量纲的物理量的相似系数均为1,即Cν=Cε=Cφ=Cν0=1[10]。
模型材料密度的相似系数Cρ=1.01,应力的相似系数Cσ=2.49,弹性模量的相似系数CE=1.99,介质波阻抗的相似系数CCρρr=0.71。
4.2.2 几何相似
由于模型体尺寸有限,而实际爆破时岩体为无限体,所以边界条件不符合几何相似原理。在尽量减小模型试验失真程度和尺寸效应对试验结果影响的前提下,将模型试件尺寸定为50 cm×50 cm×90 cm,原型炮孔深度为9 m,从而得到几何相似系数αL=10。
4.2.3 爆破动力相似
矿山爆破现场采用1 号岩石乳化炸药,此次模型试验选用导爆索作为主爆药(RDX 装药量不少于10.5 g/m),1 号岩石乳化炸药的爆力值AE为320 mL,RDX 的爆力值ARDX为480 mL,换算系数c=AE/ARDX≈0.67。对模型试验进行爆破动力相似分析[24],其爆破动力相似常数Cγ为
经计算,爆破动力相似常数Cγ为0.42。
使用力量纲F、长度量纲L、时间量纲T 作为基本量纲进行量纲分析,结果见表5,其中H为炮孔深度。

表5 量纲分析Table 5 Dimensional analysis
4.3 正交试验设计
此次模型试验选用直径为6 mm 的数码电子雷管与导爆索,炮孔直径为8、10、12、18 mm;装药结构采用径向不耦合装药形式,相应的不耦合系数为1.33、1.67、2.00 和3.00。模拟的预裂孔的L/d为9,孔深90 cm,选用数码电子雷管(每发雷管折合0.583 g RDX),设置8、10、12、15 ms 4 种延期时间。此次模型试验使用的线装药密度为2 g/m,单孔装药量为1.8 g,最大单响药量(Q)有1.8、3.6、5.4 g 3 个水平,为将单孔装药量补充至4 个水平,用1.8*表示拟最大单响药量1.8 g 水平,模型试件不填塞,充分考虑误差项对试验的影响。
本次模型试验方案采取正交设计,具体方案如表6 所示。

表6 正交试验方案设计Table 6 Orthogonal experimental scheme design
4.4 正交试验结果与分析
通过半孔率(δ)和预裂缝宽度(b)两个指标评估模型试验的爆后效果。半孔率为爆后较完整半孔长度相对于整个炮孔长度的比值,预裂缝宽度采用卷尺直接测量。试件典型爆后效果如图13 所示,正交试验结果列于表7。

表7 爆破效果统计Table 7 Statistics of blasting effects

图13 试件的典型爆后效果Fig.13 Typical blasting effect of specimens after explosion
采用极差分析法处理表7 中的试验数据,结果见表8 和表9,其中Ki(i=1, 2, 3, 4)表示因素j取第i个水平时各评价指标的平均值。

表8 正交试验极差分析(半孔率)Table 8 Extreme analysis for orthogonal experiments (half porosity)

表9 正交试验极差分析(预裂缝宽度)Table 9 Extreme analysis for orthogonal experiments (pre-split crack width)
极差Rj反映因素j对评价指标的影响程度,Rj越大,说明因素j对评价指标的影响越大。根据Rj可以确定影响预裂爆破半孔率和预裂缝宽度的主要因素是不耦合系数,其次是延期时间,最后是最大单响药量。
正交试验直观分析的具体表现形式是效应曲线。3 种因素的均值效应曲线如图14 和图15 所示。可以看出:不耦合系数与半孔率呈正相关,与预裂缝宽度整体呈负相关;最大单响药量与半孔率及预裂缝宽度均呈正相关关系;随着延期时间的增加,半孔率和预裂缝宽度均先增大后减小。

图14 半孔率的效应曲线Fig.14 Effect curves of half porosity

图15 预裂缝宽度的效应曲线Fig.15 Effect curves of pre-split crack width
在预裂爆破效果评价指标中,尽可能使半孔率较高,即不耦合系数取3.00,延期时间取12 ms,最大单响药量取5.4 g(三孔一响);同时,尽可能使预裂缝宽度较大,即不耦合系数取1.33,延期时间取12 ms,最大单响药量取5.4 g(三孔一响)。但是,较小的不耦合系数会对周边岩体造成较大损伤,综合考虑最佳预裂成缝效果,则因素组合为不耦合系数为3.00,延期时间为12 ms,最大单响药量为5.4 g(三孔一响)。
5 现场试验验证
5.1 现场预裂爆破参数选择
基于模型试验数据,结合仿真模拟研究结果,选取合理的预裂爆破参数进行现场试验,评价爆后效果。
根据矿山实际情况,选用2 号潜孔钻进行钻孔(d=89 mm),药卷直径32 mm,则不耦合系数为2.78,因模型试验的局限性,不耦合系数很难取到2.78,因此近似为3.00;根据矿山钻机情况,选取预裂孔孔距为0.8 m(L/d约为9);选用数码电子雷管,延期时间统一设定为12 ms;参考矿山爆破工程经验,结合式(6)和式(7)[13]进行计算,可得线装药密度QL约为450 g/m,因此,将此次现场预裂爆破线装药密度取为450 g/m。
式中:QL1和QL2为两种方法得到的线装药密度,单位为kg/m;预裂孔距L和炮孔直径d的单位为m;岩石抗压强度σbc的单位为MPa。
5.2 现场预裂爆破试验结果
受现场试验的限制,此次试验只设计垂直预裂孔,预裂孔与水平面成90°,钻孔深度H为9 m;取加强装药段长度为0.2H,该段装药线装药密度q0=2QL;中间正常装药段长度为0.5H,该段装药线装药密度q0=QL;上部减弱装药段长度为0.3H,q0=QL/3;装药结构采用径向不耦合装药形式,炮孔顶部设计不装药长度2 m,单孔装药量为3.75 kg。模型试验中,最大单响药量为5.4 g(三孔一响)时,半孔率和预裂缝宽度最优,所以此次现场试验同响孔数设为3,即最大单响药量为11.25 kg,爆后效果如图16 所示。

图16 大理岩预裂爆后效果Fig.16 Effect of marble after pre-splitting blasting
通过爆后效果可以看出,孔口岩石完整,没有发生破碎现象。爆破开挖后,对半孔率和不平整度进行统计,得到此次试验的半孔率为80.7%,不平整度在20 cm 左右,没有根底产生,说明预裂效果较为理想。
6 结 论
通过数值模拟结合相似模型试验确定了最佳预裂成缝效果的参数组合,并通过现场试验进行了验证,得出以下结论。
(1) 通过数值模拟可知,不耦合系数小时,爆破孔周围裂缝存在较大分岔现象,对岩体造成的损害较大,适当增大不耦合系数可降低孔壁附近的岩体损伤,起到保护孔壁的作用;延期时间不同,所产生的爆破应力不同,右侧炮孔起爆时,单元应力峰值在12 ms 时达到最大,且保留岩体不受破坏,其中双孔连线中点单元的应力峰值为42.3 MPa,较同时起爆时减小25.8%,能有效地减少对附近岩体的破坏。
(2) 正交试验分析结果表明,影响预裂爆破半孔率和预裂缝宽度的主要因素是不耦合系数,其次是延期时间,最后是最大单响药量。不耦合系数与半孔率呈正相关,与预裂缝宽度整体呈负相关;半孔率和预裂缝宽度均与最大单响药量呈正相关;随着延期时间的增加,半孔率和预裂缝宽度表现出先增大后减小的变化规律。
(3) 通过相似模型试验,得出不耦合系数为3.00、延期时间为12 ms、最大单响药量为5.4 g(三孔一响)的参数组合下,模型试件预裂成缝效果最佳。根据数值模拟、相似模型试验结合理论计算得到,孔距为0.8 m(L/d约为9)、不耦合系数为3.00、延期时间为12 ms、最大单响药量为11.25 kg(三孔一响)时,现场预裂爆破试验取得良好的预裂效果。
