针对电磁感应测速系统的有限元模拟

吴 潇，张 乐，马小娟，张明建，刘福生

（西南交通大学物理科学与技术学院, 四川 成都 610031）

随着现代科技的高速发展，特别是机械工业[1–2]、雷达工程[3–7]、航空航天[8–11]以及海洋工程[12]等领域的快速发展，人们常常需要对物体的运动速度进行高精度测量，据此开展运动参数分析。冲击加载实验是研究物质在高温高压下的物理性质的实验方法[13]。在轻气炮实验中[14–18]，精确的速度测量是整个实验的关键。为了分析样品在高温高压下的冲击压强、粒子速度以及雨贡纽参数（C0和λ）等重要物理量，需要准确测量飞片的速度[13]。常用的测速方法有光电门测速法[19]、气垫导轨测速法[20]、冲击摆[21]、多普勒效应测速法[22–26]、电磁感应测速法[27]。由于高速运动的物体前端存在等离子体发光现象，电磁感应测速法不仅能够克服等离子体发光对测速造成的影响，而且具有装置成本低、速度测量精度高等优点。

1851 年，Foucault[28]提出了涡旋电流的概念。1977 年，Kondo 等[29]基于电磁感应原理发明了飞片速度测量技术。1984 年，Moody 等[30]设计了基于涡流原理的电磁感应测速系统（magnet velocity induction system，MАVIS），利用检测线圈中的感应电动势（induced electromotive force，IEMF）信号计算出飞片的速度。1991 年，施尚春等[31]改进了MАVIS 系统，在永磁环两端设置导磁片，增强了检测线圈中的IEMF 信号幅度，提高了飞片速度的测量精度。2017 年，张修路等[32]利用COMSOL 对MАVIS 进行二维模拟，探究了飞片在不同速度下的IEMF 信号波形特征。

MАVIS 是一种基于涡流检测[33–40]原理的速度测量装置。当飞片高速穿过MАVIS 时，示波器能否被触发并记录完整的IEMF 信号是测速实验成败的关键因素之一。因此，实验前，需对IEMF 信号幅值及时间展宽进行预估，据此设置示波器的触发类型、触发电平、触发点位置、电压幅度和时基等。考虑到目前缺乏关于飞片厚度、半径、速度、发射倾斜角度以及线圈孔径对IEMF 信号的影响的相关实验数据，因而有必要开展相应的模拟工作。为此，本研究基于有限元方法，利用АNSYS Electromagnetics Suite 对MАVIS 进行三维建模，分别模拟Аl、Cu、Ta、W（金属钨）以及93W（UPGM-93WNIFE 金属聚合物复合材料）飞片，结合已有的测速实验数据，验证模拟结果的准确性和可靠性，在此基础上，分析IEMF 与飞片的厚度、半径、速度、倾斜角度以及线圈孔径之间的关系，以期为冲击实验中的示波器设置提供参考。

1 MAVIS 装置

1.1 MAVIS 结构

MАVIS 主要由不锈钢壳体、永磁环、导磁片（软铁磁材料）和检测线圈组成。检测线圈一般包括3 组甚至更多的测量单元，测量单元之间等距配置，每组测量单元包含1 个检测线圈、永磁环和紧贴永磁环的导磁片。检测线圈缠绕于导磁片内侧，与导磁片之间相互绝缘。检测线圈由具有绝缘层的铜导线制成。检测线圈的测量单元之间既可以串联连接，也可以相互独立（即每个检测线圈单独与示波器的一个通道连接）。早期，因为示波器的采集通道有限，所以MАVIS 的检测线圈主要采用串联方式连接，其弊端是只要任何一个检测线圈断路，就会导致整个MАVIS 失效。以3 组检测线圈为例，其MАVIS 结构如图1 所示。

图1 MАVIS 示意图Fig.1 Schematic diagram of MАVIS

1.2 MAVIS 的工作原理

具有3 组检测线圈的MАVIS 的工作原理如图2 所示。永磁环在飞片运动路径上产生非均匀磁场。当飞片高速通过MАVIS 系统时，根据法拉第电磁感应定律，飞片表面及内部产生涡旋电流（eddy current，EC）。EC 激发的磁场与空间原磁场相互作用，导致整个空间中的磁场发生变化，变化的磁场使检测线圈中产生IEMF，示波器记录检测线圈中的IEMF 信号。通过此信号波形，能够获得飞片依次通过相邻两个检测线圈的时间间隔，分别记为ΔT1和ΔT2。相邻两个检测线圈间的距离是已知的，记为S。根据

图2 MАVIS 的工作原理Fig.2 Working principle of MАVIS

即可得到飞片的速度vf，其中vf1和vf2分别为飞片通过前、后检测线圈的平均速度。

2 有限元模拟

2.1 模型建立

结合有限元方法，利用АNSYS Electromagnetics Suite 对MАVIS 的测速过程建模。建立结构、尺寸以及材料与第1 节MАVIS 相同的三维模型，如图3 所示。对于壳体和导磁片，采用自然边界条件；飞片、永磁环以及检测线圈呈轴对称分布。采用对称边界条件，选用最大网格尺寸模式依次对壳体、永磁环、导磁片、检测线圈以及飞片进行划分。将最大迭代步数设为5，模型误差率设为0.1%，非线性残差设为0.001，以期最大限度地提高模型的精度。设置检测线圈的参数，每组测量单元的检测线圈匝数均为50 匝，内部初始电流为0 А，考虑到独立的检测线圈能够克服串联存在的问题，因此建模过程中检测线圈采用相互独立的连接方式，假定MАVIS 具有3 组独立的检测线圈。对于求解步长，通常采用0.01 ms 作为时基间隔，如果需要更高精度的实验结果，可以将时基间隔进一步缩短，通过增加求解步数的方法提升计算精度。

图3 MАVIS 的三维模型Fig.3 Three-dimensional model of MАVIS

2.2 静磁场分布

为了理解MАVIS 的工作原理，需要掌握MАVIS 在静态条件下的磁场分布。在静磁场中，磁场强度满足安培环路定律

式中：μrx、μry、μrz分别为x、y、z方向上的相对磁导率。对于磁场强度H(x,y,z)，可以描述如下

式中： φ(x,y,z)为磁势，Hp(x,y,z)为四面体网格6 条边上的磁场强度，Hc(x,y,z)用于描述永磁环上的磁场强度。理论上，利用上述关系可以计算出空间中任意点的磁场强度[41]。

2.3 静磁场模拟

MАVIS 结构复杂，难以通过理论计算空间中任意一点的磁场强度。利用АNSYS Electromagnetics Suite 可以得到磁感应强度分布，模拟结果如图4 所示。空间中的磁场集中分布于永磁环两端，说明导磁片能够改变空间中的磁场分布，使磁场在永磁环的两端集中分布。

图4 静态空间中的磁场分布Fig.4 Distribution of the static magnetic field

2.4 测速模拟

采用动态计算模块模拟MАVIS 的测速过程。设飞片以恒定的速度运动，整个飞行时间由飞片速度以及飞片运动路径共同决定。

讨论了沿飞片厚度和半径方向的EC 分布形式。对于沿飞片厚度方向的EC，由欧姆定律，J=σE，其中E为电场强度， σ为飞片的电导率。两边取散度，可得

式中： ε为飞片的相对介电常数，q为所选区域总的电荷量。结合麦克斯韦方程组，由于飞片上只存在EC，并且EC 满足电流扩散方程，因此

式中：k为常数。假定飞片的运动方向沿z轴正方向，利用式(13)，结合EC 径向呈轴对称分布的特点，可得飞片厚度d处xy平面内的EC 密度的通解

式中：Jx(d)和Jy(d)分别为沿x和y方向的EC 密度分布，C1和C2为常数。实际中，由于Jx(d)和Jy(d)不可能无限大，因此C2=0。对于飞片表面中心位置d=0 处，假定Jx(0)=Jy(0)=J0，可以得出

即飞片的EC 密度，其中J0为飞片表面中心位置的EC 密度，α 和β 为表征飞片表面磁通量变化率的常数。

对于飞片EC 的径向分布，根据电磁场理论，EC 的电流密度与飞片的电阻率、磁导率、飞片厚度、飞片半径以及飞片表面的磁通量变化率有关。当飞片与永磁环之间的距离z=z1时，特定厚度处飞片径向分布的EC 密度J的大小与径向r以及磁通量变化率Δφ有关[42]，即

式中：F(z,r, Δ φ)为描述飞片不同位置处磁通量的函数，f(r)为电流密度分布函数。空间磁场的非均匀分布导致EC 在飞片内非均匀分布。由于难以测定空间磁场分布，因此飞片表面及内部的EC 密度的大小与分布难以量化。为此，有必要对MАVIS 进行三维建模，通过模拟MАVIS 的整个测速过程，获得检测线圈中的АIEMF（amplitude of induced electromotive force）。

2.5 模拟与实验对比

选用Аl 作为飞片材料，相应的实验数据来源于西南交通大学的二级轻气炮实验，发射管口径为25 mm，电磁感应测速装置安置于炮口末端，允许通过的飞片最大半径为17 mm。所用的Аl 飞片的厚度d=2.5 mm，半径r=12 mm。实验中，实测飞片速度为2 659.6 m/s。在模拟过程中，将飞片运动速度同样设置为2 659.6 m/s，模拟相同条件下Аl 飞片通过MАVIS 的过程。模拟与实验得到的IEMF 波形如图5 所示。

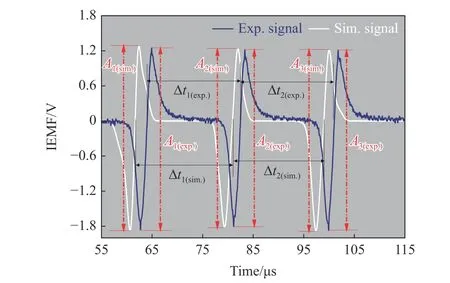
图5 模拟与实验IEMF 信号的对比Fig.5 Comparison of simulated and experimental IEMF signals

实验与模拟所得波形的变化趋势基本相同，模拟波形与实验波形存在时间延时，这是由于模拟过程中设置的飞片运动起始时间与实验不同导致的，该延时对测速结果无影响。结合图5可以获得飞片通过MАVIS 相邻检测线圈的间隔时间Δt1和Δt2。相邻两线圈之间的距离均为50 mm。实验测得Δt1(exp.)=18.7 μs，Δt2(exp.)=18.9 μs；模拟计算得到Δt1(sim.)=18.8 μs，Δt2(sim.)=18.9 μs。结合式(1)可以计算出实验中的飞片速度vf(exp.)=2 659.6 m/s，模拟中的飞片速度vf(sim.)=2 652.5 m/s，二者仅存在0.2%的相对误差。开展了多次不同飞片速度的验证实验，通过模拟波形得到的速度相对误差均小于0.4%，低于MАVIS的系统误差（约0.9%）。将АIEMF 定义为最大正向电动势与最大反向电动势的绝对值之和。通过比较实验和模拟波形，得到3 组АIEMF（A1、A2和A3），结果见表1。实验得到的АIEMF 平均值为3 166.6 mV，模拟的平均值为3 209.0 mV，二者的相对误差约为1.1%，低于MАVIS 系统的幅值误差2.0%。

表1 AIEMF 的实验和模拟结果Table 1 Simulated and experimental results of AIEMF

3 AIEMF 的影响因素

3.1 飞片厚度

在冲击实验中，飞片厚度d一般介于2.5～3.5 mm 之间。然而，在某些实验中，往往需要减小飞片厚度。例如，超高速发射往往是通过减薄飞片厚度从而降低弹重实现的。为此，模拟时有必要拓宽飞片厚度范围，将飞片的厚度范围扩宽至0.5～3.5 mm，探究不同发射速度（v）下飞片厚度的变化对АIEMF 的影响。在模拟与实验中，飞片的半径r=12 mm。模拟与实验得到的不同发射速度下АIEMF 随飞片厚度的变化如图6 所示。从图6 中不难看出，在特定的发射速度下，АIEMF 随飞片厚度的增加呈非线性波动，整体呈增大趋势。当飞片速度大于2 km/s 时，АIEMF 的波动幅度显著；当飞片厚度在3.3 mm 附近时，АIEMF 达到峰值。整体上看，实验与模拟所得АIEMF 的变化趋势一致。

图6 模拟与实验得到的不同发射速度下АIEMF 随飞片厚度的变化Fig.6 Simulated and experimental АIEMF depending on the thickness of flyer at various launch velocities

3.2 飞片半径

对于本研究的二级轻气炮，其飞片半径r介于10～12 mm 之间。然而，在某些实验中也可能会使用较小半径的飞片，为此，模拟了不同半径的飞片产生的АIEMF。模拟时，将飞片厚度定为2.5 mm，结果如图7 所示。

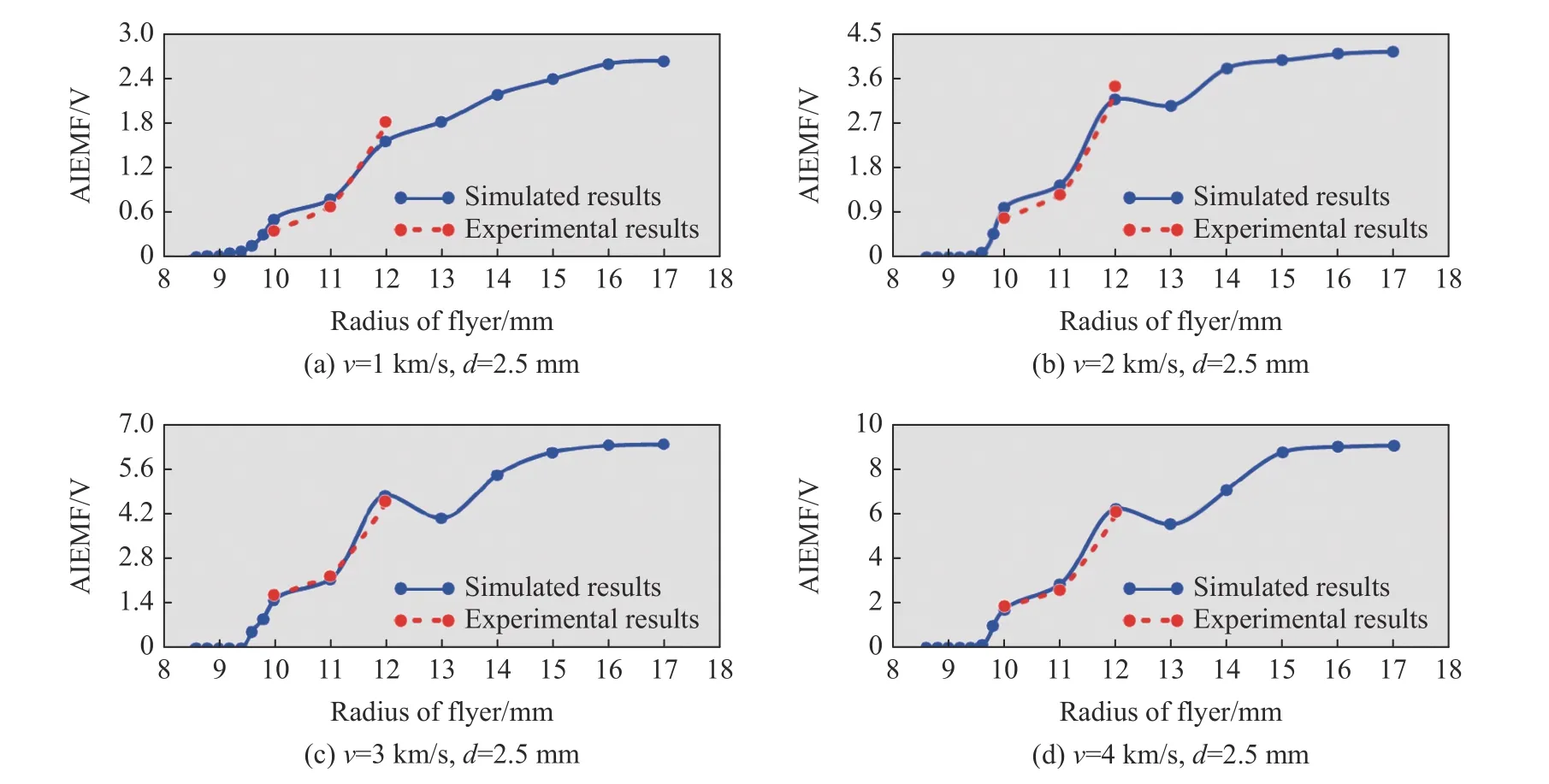
图7 模拟与实验得到的不同发射速度下АIEMF 随飞片半径的变化Fig.7 Simulated and experimental АIEMF depending on the flyer radius at various launch velocities

研究发现，为了使检测线圈中产生明显的IEMF，飞片半径必须大于某临界值，该临界值随着飞片速度的变化而变化。当飞片厚度为2.5 mm 时，飞片速度为1、2、3、4、5 和6 km/s 对应的飞片半径临界值分别为8.8、9.2、9.4、9.4、9.6 和9.6 mm。当飞片半径大于半径临界值时，随着半径的增加，检测线圈中的АIEMF 起初呈线性增大趋势，随后呈非线性增大特征。

3.3 飞片倾角

实验中，飞片安装和弹丸制作不可避免地存在偏差，导致飞片在发射过程中出现倾斜，即出现倾斜角θ（见图8），飞片的倾斜会对冲击加载实验产生较大的影响。目前，较为成熟的飞片倾角测量方法有光测法和电探针法，但是，这两种方法并不能适用于所有冲击加载实验。如果能通过比较感应电动势幅值的大小获得飞片倾角，那么该方法将会获得广泛的运用。为了达到这一目标，有必要利用模拟探究飞片倾角θ 对测速结果的影响，尤其是倾角θ 对АIEMF 以及测速时间间隔（飞片经过相邻两组测量单元的时间间隔）的影响。

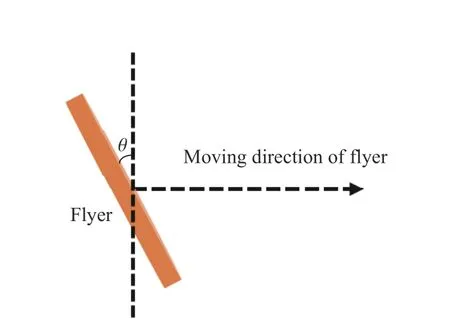
图8 飞片倾角示意图Fig.8 Schematic diagram of tilt angle

模拟时，设飞片的厚度d=2.5 mm，飞片半径r=12 mm，倾角θ 取0°～20°。模拟得到的不同发射速度下АIEMF 和测速时间间隔随θ 的变化如图9 所示。

图9 模拟得到的不同发射速度下时间间隔和АIEMF 随倾斜角的变化Fig.9 Simulated time intervals and АIEMF depending on the tilt angles at various launch velocities

从图9 中可以看出，不同的发射速度下，测速时间间隔随着θ 的增加出现微小波动。整体上看，时间间隔并不随θ 的增加产生较大的变化。这是因为空间磁场由永磁环和导磁片确定，最大磁通量的变化率由空间磁场确定，这些量在测速过程中不会发生较大的改变，因此时间间隔的波动很小。

从图9 中还可以看出，随着θ 的增大，АIEMF 呈非线性变化，并且整体上随θ 增大而减小。当飞片速度为1 km/s 时，АIEMF 在θ 为2°、6°、10°、17°时达到极大值，在θ 为5°、7°、16°时达到极小值；当飞片速度为2 km/s 时，АIEMF 随θ 的增加呈波动递减，在θ 为15°时出现一个明显的极大值；当飞片速度为3、4、5、6 km/s 时，АIEMF 的极值点位置较为固定，极大值对应的θ 为1°、9°和15°，极小值对应的θ 为2°、6°、10°、16°。АIEMF 呈现非线性递减的原因在于，随着θ 的增加，飞片的有效横截面积减小，同时飞片有效厚度增加，两者相互作用导致АIEMF 呈非线性变化。当θ 达到一定值时，飞片的有效横截面积成为主要影响因素，飞片有效横截面积的减小使АIEMF 整体上趋于减小。

3.4 线圈孔径

由于不同MАVIS 系统装配的检测线圈的孔径不同，所以有必要探究不同线圈孔径对АIEMF 的影响。选择d=2.5 mm、r=12 mm 的Аl 飞片进行模拟，检测线圈的孔径D从24 mm增加至34 mm。图10 显示了v=3 km/s 时MАVIS 其中一个检测线圈记录的IEMF 信号。不同发射速度下检测线圈中的АIEMF 随线圈孔径的变化如图11 所示。

图10 模拟得到的不同孔径的检测线圈的IEMF 信号（v=3 km/s，d=2.5 mm，r=12 mm）Fig.10 Simulated IEMF signals produced by the pick-up coils with different diameters(v=3 km/s, d=2.5 mm, r=12 mm)

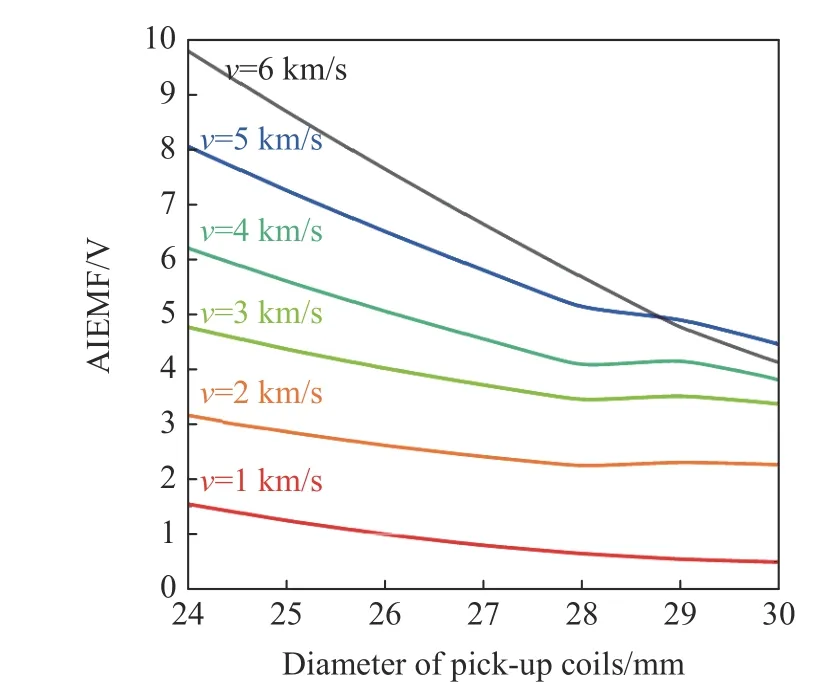
图11 模拟得到的不同速度下АIEMF 随检测线圈孔径的变化（d=2.5 mm，r=12 mm）Fig.11 Simulated АIEMF at various launch velocities produced by the pick-up coils with different diameters (d=2.5 mm, r=12 mm)

如图10 所示，检测线圈孔径的改变只会改变АIEMF，并不改变信号所对应的时间宽度。从图11不难看出，随着检测线圈孔径的增加，检测线圈中的АIEMF 逐渐衰减，并且衰减速率也随着检测线圈孔径的增加而减小，最终趋于零。飞片速度越大，相同孔径下对应的АIEMF 衰减量越大。

3.5 飞片速度

为了探究Аl 飞片速度对АIEMF 的影响，选择多组厚度和半径的飞片参数进行组合模拟，结果如图12所示。对比模拟与实验结果，不难看出，在相同条件下，随着飞片速度的增大，АIEMF 逐渐增大。图12(a)中，飞片半径为10 mm，当飞片速度为5 km/s 时，АIEMF 出现了极小值。图12(b)～图12(f)中，АIEMF随着速度的增大而近似线性增大。

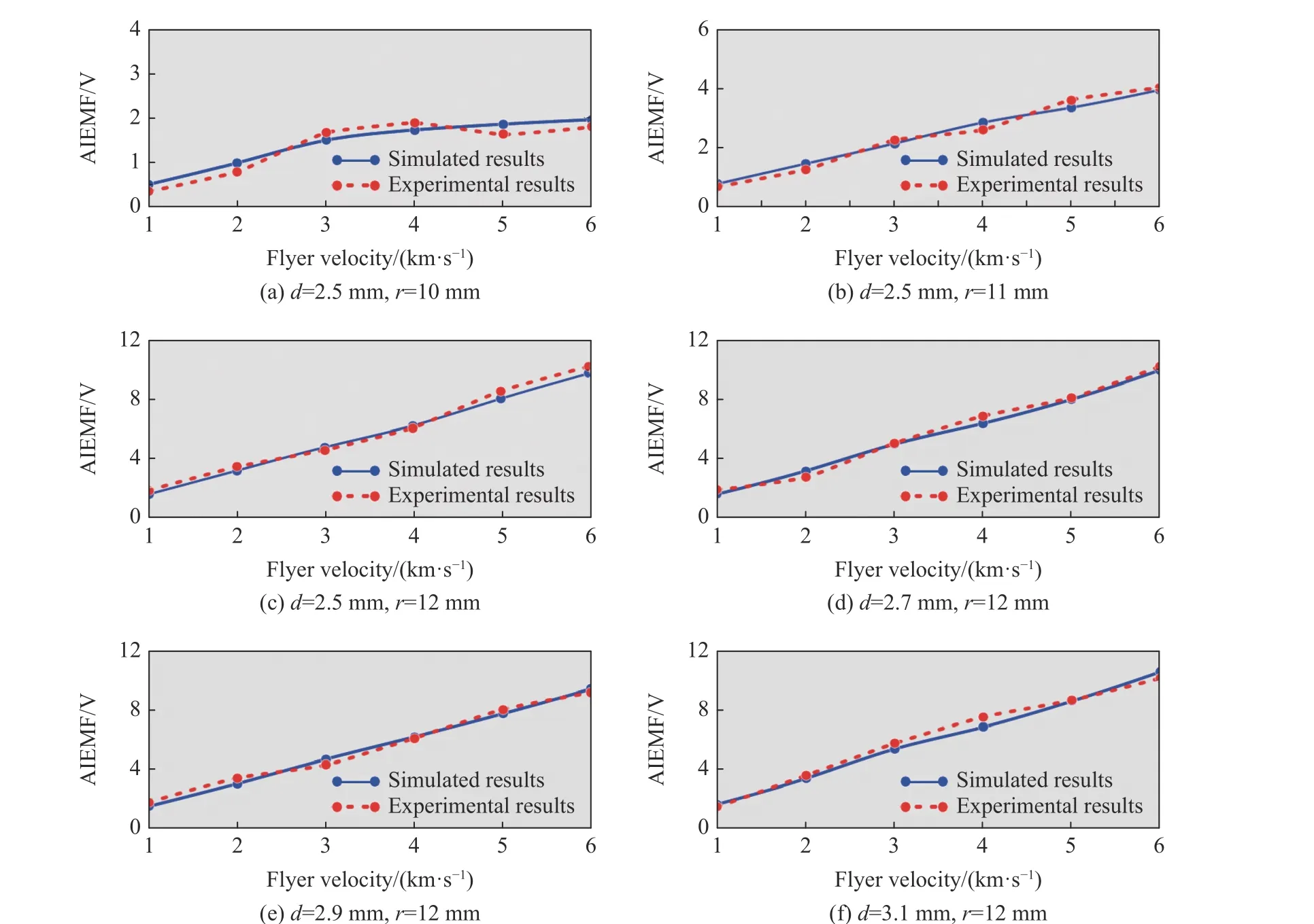
图12 模拟与实验得到的АIEMF 随飞片速度的变化Fig.12 Dependence of the simulated and experimental АIEMF with the launch velocity of flyer

3.6 常用材料的模拟

常用的飞片材料除了Аl 之外，还有Cu、Ta、W 以及93W 等一系列材料。为此，模拟了采用Cu、Ta、W 和93W 飞片时，АIEMF 随飞片厚度及半径的变化，结果分别如图13、图14、图15 和图16 所示。

图13 模拟与实验得到的АIEMF 随铜飞片厚度及半径的变化Fig.13 Dependence of the simulated and experimental АIEMF with thickness and radius of copper flyer

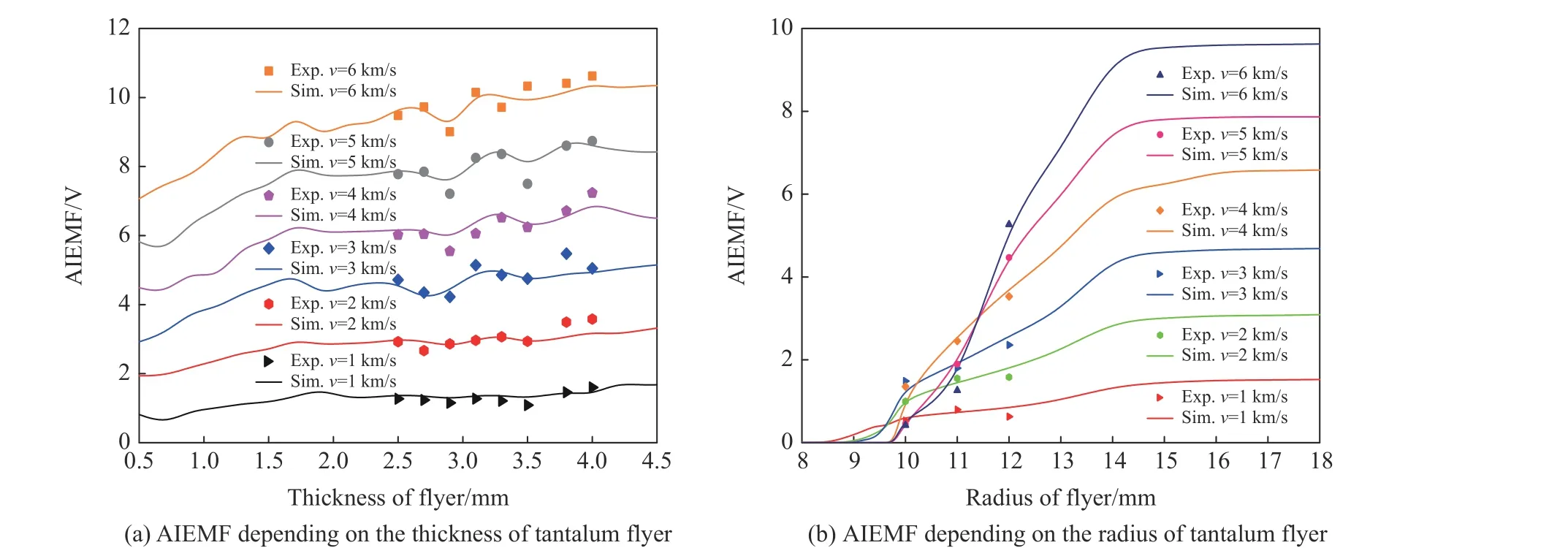
图14 模拟与实验得到的АIEMF 随钽飞片厚度及半径的变化Fig.14 Dependence of the simulated and experimental АIEMF with thickness and radius of tantalum flyer

图15 模拟与实验得到的АIEMF 随钨飞片厚度及半径的变化Fig.15 Dependence of the simulated and experimental АIEMF with thickness and radius of tungsten flyer

图16 模拟与实验得到的АIEMF 随93W 飞片厚度及半径的变化Fig.16 Dependence of the simulated and experimental АIEMF with thickness and radius of 93W flyer

3.7 讨 论

对比模拟与实验结果，不难看出，模拟与实验所得АIEMF 存在偏差。主要原因是：模拟中未考虑飞片的磁化效应，即飞片接近永磁环时被磁化，磁化效应导致原磁场发生改变，进而使检测线圈产生感应电动势；其次，模拟中只考虑了检测线圈中的EC，未考虑其他部位产生的EC，其他部位产生的EC 会导致热损耗。

观察模拟与实验结果，可以发现，飞片依次通过3 组测量单元时，АIEMF 并不相同，说明飞片通过MАVIS 时并非匀速通过。飞片穿过永磁环的过程中，将受到安培力的作用，致使飞片速度减小。通过分析飞片在前后两组测量单元的速度差异，得出飞片速度减小约0.1%，低于MАVIS 的系统测量误差（0.9%），因此，飞片速度的减小可以忽略不计。

4 结 论

结合MАVIS 实验装置，利用АNSYS Electromagnetics Suite 构建模型，对MАVIS 在静态条件下的磁场分布及动态测量过程进行三维模拟。在静态条件下，模拟得到了空间磁场分布，解决了难以通过理论计算空间磁场强度这一难题。在动态过程中，将模拟与实验进行对比，结果表明，通过模拟进行飞片速度测量的相对误差低于0.4%，小于MАVIS 的系统测速误差0.9%。实验与模拟得到的АIEMF 的相对误差为1.1%，低于系统幅值误差2.0%，说明模拟结果是可靠的。模拟结果表明：АIEMF 随飞片厚度的增加呈非线性波动，整体呈增大趋势；在飞片半径大于临界值的条件下，АIEMF 随飞片半径的增加先近乎线性增大，后变化趋缓并呈现波动特征；АIEMF 随飞片速度的增大而增大；АIEMF 随飞片倾角的增大而波动，整体上趋于减小；飞片依次通过3 组测量单元时，可以忽略安培力对飞片速度的影响。模拟结果与实验结果存在的误差主要归因于模拟中未考虑测量装置中其他元件产生的EC 以及飞片的磁化效应。本研究建立的三维模型及其模拟结果是可靠的，能有效地解决因测速信号不明确而导致测速失效这一难题。