聚龙一号上磁驱动铝飞片发射实验的数值分析与再设计*

阚明先,杨 龙,段书超,王刚华,肖 波,张朝辉,王贵林

(中国工程物理研究院流体物理研究所，四川 绵阳 621999)

聚龙一号上磁驱动铝飞片发射实验的数值分析与再设计*

阚明先,杨 龙,段书超,王刚华,肖 波,张朝辉,王贵林

(中国工程物理研究院流体物理研究所，四川 绵阳 621999)

聚龙一号上PTS-151发次实验中，磁驱动加速370 μm厚飞片测得的最大速度为18 km/s，磁驱动加速482 μm厚飞片测得的最大速度为19 km/s。采用MDSC2程序,对PTS-151发次实验进行了数值分析，结果表明：PTS-151发次实验中测量的最大速度的含义不同于以往文献中飞片的最大速度。以往文献中发射飞片在测试过程中自由面未被烧蚀，测试的最大速度为飞片自由面速度；PTS-151发次实验中两个飞片在测量过程中自由面被烧蚀，实验测量的最大速度为飞片被完全烧蚀前的一瞬间飞片内部最后一个固体面的速度。在飞片自由面未被烧蚀之前，370 μm厚飞片的计算最大自由面速度仅为7 km/s，482 μm厚飞片的计算最大自由面速度仅为11.8 km/s，远低于测量值。对PTS-151发次实验条件下飞片尺寸进行了再设计，飞片厚度为680 μm时最优，既能保证自由面未烧蚀，又使得飞片的速度最大，达到17.5 km/s。

聚龙一号装置；磁驱动飞片；二维磁驱动数值模拟程序；固体反射面；自由面速度

自1999年，利用Z装置进行平面等熵压缩和磁驱动飞片发射实验以来，磁驱动高速飞片发射技术取得了飞速发展。R.W.Lemke等[1]在ZR装置上驱动铝飞片获得了45 km/s的超高速度。磁驱动高速飞片发射技术主要用于等熵/冲击压缩实验，有助于材料的高压物态方程、高能量密度物理和武器物理等研究[1-10]。数值模拟是磁驱动飞片发射技术研究的重要工具，不仅能模拟实验结果、加深对实验现象的理解、对物理过程的认识，并能设计出合适的电流波形和飞片尺寸，既保证获得最大的飞片自由面速度，又保证飞片自由面部分不被烧蚀，处于固体状态。R.W.Lemke等[1-2,4-5]、M.D.Knudso等[6]利用磁流体力学程序进行了许多理论工作。

二维磁驱动数值模拟程序MDSC2[11]是二维四边形交错网格上的磁流体力学拉格朗日程序。MDSC2程序中采用算子分裂法把磁流体力学方程组依次分成热扩散、磁扩散、理想流体力学等物理过程，每个物理过程采用有限差分方法和有限体积方法离散，其求解方法参见文献[11]。MDSC2程序能够正确模拟自由面保持固体状态的磁驱动发射飞片实验[11-12]。阚明先等[13]采用MDSC2程序，解决了自由面烧蚀情况下磁驱动发射飞片的模拟，揭示了自由面烧蚀时实验测量的速度为固体反射面速度的事实。本文中，采用MDSC2程序对聚龙一号上的PTS-151发次磁驱动发射飞片实验进行计算分析，确定PTS装置在PTS-151发次实验条件下的结构参数，并对PTS-151发次实验条件下的发射飞片尺寸进行设计，既要保持飞片在测试过程中自由面部分未被烧蚀，又要使发射飞片具有更高的飞行速度。

1 实验配置

聚龙一号是超高功率、多路并联运行的大电流脉冲装置[14]。它具有短脉冲、长脉冲和波形调节等3种工作模式，输出脉冲前沿90～400 ns，最大输出电流8～10 MA，已用于Z箍缩、磁驱动高速飞片发射和磁驱动准等熵压缩等实验。

PTS-151发次实验是聚龙一号上的磁驱动铝飞片发射实验，实验结构如图1所示。阴、阳极板宽为7.2 mm ,阴阳极板之间的间隙为1.2 mm，阴阳极板都为铝材料，阳极板上嵌入两个半径为3.5 mm的圆形铝飞片，一个飞片厚370 μm，另一个飞片厚482 μm。采用激光速度干涉仪(VISAR)测量飞片速度历史。对于370 μm的飞片，VISAR测量的最大速度为18 km/s；对于482 μm的飞片，VISAR测量的最大速度为19 km/s。

2 数值模型

二维磁驱动数值模拟程序MDSC2的控制方程为：

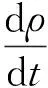
(1)

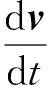
(2)

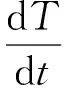
(3)

(4)

式中：ρ、T、v分别为流体的密度、温度和速度；B为磁感应强度；η为电阻率[15]；p为压强；σ为人工黏性张量，ke为热扩散系数，cV为比热容，μ0为真空磁导率。d/dt为Lagrangian导数：

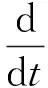
(5)

对于磁驱动飞片，加载面上的磁压力为：

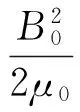
(6)

加载面上的磁感应强度B0为：

B0=μ0fiI(t)/S

(7)

式中：I(t)为实验电流，fi为PTS装置的结构系数,S为自由参数。

3 数值结果

采用MDSC2程序，对聚龙一号上PTS-151发次磁驱动发射飞片实验进行了数值模拟。

图2为PTS-151发次实验的电流波形，图3 为370 μm飞片的计算和实验测量的速度。从图3可知，计算的飞片自由面速度与固体反射面速度不相同，飞片自由面已被烧蚀熔化，计算的固体反射面速度与VISAR测量速度更加一致，VISAR测量的速度不是飞片自由面速度，而是飞片固体反射面速度[13]。在340 ns前，飞片自由面保持固体状态，VISAR测量的速度为飞片自由面速度；在340～410 ns之间，在焦耳热的作用下，飞片自由面被烧蚀，密度低于固体密度，VISAR的探针激光穿过低于固体密度的部分，到达距离飞片自由面最近的固体密度位置再反射回去，获得固体反射面的速度；在410ns后，VISAR无法测量飞片任何位置的速度。410 ns时370 μm的飞片的密度分布如图4所示。图中右边为飞片的电流加载面,左边为飞片的自由面(下同)。从图4可知，飞片自由面和电流加载面的密度较低，自由面和加载面之间的中间部分的密度较高，飞片的最大密度已低于2.5 kg/m3，飞片已被完全烧蚀。因此， 370 μm飞片的最大测量速度是飞片完全烧蚀的瞬间飞片内部最后一个固体反射面的速度。

图5为482 μm飞片的计算和实验测量的速度。从图5可知，在速度测量过程中，计算的飞片自由面速度与固体反射面速度不完全相同，飞片自由面已被烧蚀，实验测量速度也为飞片固体反射面速度。在389 ns前，飞片自由面未被烧蚀，VISAR测量的速度为飞片自由面速度；在389～470 ns之间，飞片自由面已被烧蚀， VISAR测量的速度为飞片自由面之后的固体反射面的速度；在470 ns后， VISAR无法测量飞片任何位置的速度。

图6为470 ns时482 μm飞片的密度分布。从图6可知，482 μm飞片两边的密度较低，中间的密度较高，飞片的最大密度已低于2.5 kg/m3，飞片已被完全烧蚀。因此，482 μm的飞片的最大测量速度也是飞片完全烧蚀的瞬间飞片内部最后一个固体反射面的速度。

实验电流是靶室外测量的电流，飞片飞行过程中会增加回路的感抗，导致实际流过负载的电流下降，再加上磁场泄露等原因，实际流过飞片加载面的电流比测量电流小，二维计算时使用实际流过飞片加载面的有效电流[6]。流过飞片加载面的有效电流与实验测量电流之间的比值，叫做装置的结构系数。数值模拟表明：PTS-151发次实验中，飞片的结构系数与飞片的厚度有关，不同厚度飞片的结构系数是不同的。482 μm的飞片的结构系数为0.595，370 μm的飞片的结构系数为0.57。

采用MDSC2程序，对Z装置上的磁驱动发射飞片实验进行了数值模拟。图7为Z装置上Z2434发次实验[10]2.004 mm铝飞片的计算和实验测量的速度。从图7可知，Z2434发次实验飞片的自由面速度与固体反射面速度一致，飞片自由面未被烧蚀，VISAR测量的速度为飞片自由面速度。图8为Z2434实验3 200 ns时飞片的密度分布。从图8可知，在测量结束时，即测量速度的最大值时，Z2434实验中飞片的自由面仍保持固体状态。因此，Z2434实验中飞片最大速度是测试结束时刻的飞片自由面速度。Z装置上的其他磁驱动发射飞片，例如文献[1-5]中飞片的最大速度都是测试结束时刻的飞片自由面速度，飞片自由面到测量结束时仍保持固体状态。

4 实验设计

由上可知，Z装置上磁驱动飞片实验和聚龙一号装置上PTS-151发次实验测得的飞片最大速度的含义是不同的。Z装置上磁驱动飞片实验测得的飞片最大速度是测试结束时刻的飞片自由面速度，在测试过程中，飞片自由面始终保持固体状态；PTS-151发次实验中370 μm和482 μm的两个飞片测得的最大速度不是飞片自由面速度，而是飞片完全烧蚀瞬间飞片内部最后一个固体面的速度。由计算可知，在PTS-151发次实验中：370 μm的飞片自由面未烧蚀时的最大速度仅为7 km/s，340 ns以后飞片自由面已被烧蚀；482 μm的飞片自由面未烧蚀时的最大速度仅为11.8 km/s，389 ns以后飞片自由面已被烧蚀。同一电流驱动不同厚度的飞片，获得的自由面未烧蚀时的最大速度是不同的。

为了确定在PTS-151发次实验条件下，飞片尺寸为多大时，在整个发射过程中飞片自由面不被烧蚀，始终保持固体密度状态，并且获得的速度最大，采用二维磁驱动数值模拟程序MDSC2，对飞片尺寸进行了再设计。表1为PTS-151发次实验条件下不同厚度飞片的计算结果，表中h为飞片厚度，k为装置结构系数，tf为自由面烧蚀时间，vf为未烧蚀固体自由面的最大速度。由于不同厚度飞片的装置结构系数是不同的，表1中不同厚度飞片的装置结构系数采用370 μm和482 μm飞片装置结构系数的线性插值进行预测。

从表1可知，飞片厚度在680 μm以下时，在实验发射过程中，飞片自由面将被烧蚀，通常意义的飞片速度即未烧蚀的固体自由面飞片的最大速度随着厚度的增加而增大；飞片厚度在680 μm时，在实验发射过程中，飞片自由面不被烧蚀，可获得的通常意义的飞片速度最大，达到17.5 km/s；飞片厚度在680 μm以上时，在发射过程中，飞片自由面不被烧蚀，通常意义的飞片速度即未烧蚀的固体自由面飞片的最大速度随着厚度的增加而减小。因此，在PTS-151发次实验条件下，680 μm厚的飞片最优，既能保证自由面不被烧蚀，又能获得最高的飞片速度，约17.5 km/s。

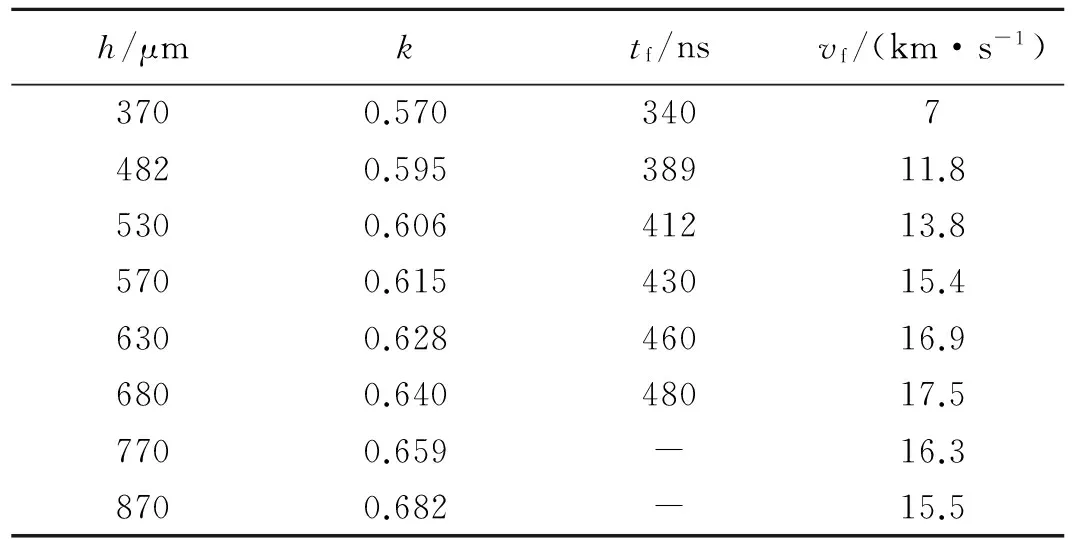
表1 不同厚度未烧蚀固体自由面的最大速度Table 1 Maximum velocities of solid free-surface offlyer plates with different thickness

5 结 论

采用MDSC2程序，对聚龙一号上PTS-151发次磁驱动铝飞片实验进行了数值分析和再设计。数值模拟表明，PTS-151发次实验过程中,370 μm厚和482 μm厚两个发射飞片自由面都被烧蚀， VISAR测量的速度历史不是飞片的自由面速度历史，而是自由面之后的固体反射面速度历史。PTS-151发次实验中测量的最大速度不同于文献[1-2,4-5,10]中飞片的最大速度：文献中发射飞片的最大速度为自由面速度；PTS-151发次实验中测量的最大速度为飞片被完全烧蚀前一时刻飞片内部最后一个固体面的速度。装置的结构系数与飞片厚度有关，越厚的飞片装置结构系数越大。482 μm厚飞片的结构系数为0.595，370 μm厚飞片的结构系数为0.57。采用MDSC2程序，对PTS-151发次实验条件下的飞片厚度进行了再设计。在PTS-151发次实验条件下，当飞片厚度小于680 μm时，飞片自由面将被烧蚀；当飞片厚度大于680 μm时，飞片自由面将一直保持固体密度状态，并且随着飞片厚度的增加，获得的飞片自由面最大速度将减小；当飞片厚度为680 μm时，既能保证飞片自由面部分不被烧蚀，又能获得最大的飞片速度。PTS-151发次实验下最优飞片尺寸为680 μm，可获得最大飞片速度为17.5 km/s。

[1] Lemke R W, Knudson M D, Davis J P. Magnetically driven hyper-velocity launch capability at the Sandia Z accelerator[J]. International Journal of Impact Engineering, 2011,38(6):480-485.

[2] Lemke R W, Knudson M D，Robinson A C, et al. Self-consistent, two-dimensional, magneto-hydrodynamic simulations of magnetically driven flyer plates[J]. Physics of Plasmas, 2003,10(5):1867-1874.

[3] Matzen M K, Sweeney M A, Adams R G, et al. Pulsed-power-driven high energy density physics and inertial confinement fusion research[J]. Physics of Plasmas, 2005,12:055503.

[4] Lemke R W, Knudson M D, Hall C A, et al. Characterization of magnetically accelerated flyer plates[J]. Physics of Plasmas, 2003,10(4):1092-1099.

[5] Lemke R W, Knudson M D, Bliss D E, et al. Magnetically accelerated, ultrahigh velocity flyer plates for shock wave experiments[J]. Journal of Applied Physics, 2005,98:073530.

[6] Knudson M D, Hanson D L, Bailey J E, et al. Equation of state measurements in liquid deuterium to 70 GPa[J]. Physical Review Letters, 2001,87:225501.

[7] Knudson M D, Lemke R W, Hayes D B, et al. Near-absolute Hugoniot measurements in aluminum to 500 GPa using a magnetically accelerated flyer plate technique[J]. Journal of Applied Physics, 2003,94(7):4420-4431.

[8] Knudson M D, Hanson D L, Bailey J E, et al. Use of a wave reverberation technique to infer the density compression of shocked liquid deuterium to 75 GPa[J]. Physical Review Letters, 2003,90:035505.

[9] Knudson M D, Hanson D L, Bailey J E, et al. Principal Hugoniot, reverberating wave, and mechanical re-shock measurements of liquid deuterium to 400 GPa using plate impact techniques[J]. Physical Review B, 2004,69:144209.

[10] Davis J P, Brown J L, Knudson M D, et al. Analysis of shockless dynamic compression data on solids to multi-megabar pressures: Application to tantalum[J]. Journal of Applied Physics, 2014,116:204903.

[11] 阚明先,王刚华,赵海龙,等.磁驱动飞片二维磁流体力学数值模拟[J].强激光与离子束,2013,25(8):2137-2141.

Kan Mingxian, Wang Ganghua, Zhao Hailong, et al. Two dimensional magneto-hydrodynamic simulations of magnetically accelerated flyer plates[J]. High Power Laser and Particle Beams, 2013,25(8):2137-2141.

[12] 阚明先,王刚华,张红平,等.磁驱动高速飞片模拟中滑移界面处理[J].强激光与离子束,2015,27:015002.

Kan Mingxian, Wang Ganghua, Zhang Hongping, et al. Sliding interface processing in simulation on magnetically driving high speed flyer[J]. High Power Laser and Particle Beams, 2015,27:015002.

[13] 阚明先,张朝辉,段书超,等.“聚龙一号”装置上磁驱动铝飞片实验的数值模拟[J].强激光与离子束,2015,27(12):014001.

Kan Mingxian, Zhang Zhaohui, Duan Shuchao, et al. Numerical simulation of magnetically driven aluminum flyer plate on PTS accelerator[J]. High Power Laser and Particle Beams, 2015,27(12):014001.

[14] 夏明鹤,计策,王玉娟,等.PTS装置工作模式及波形调节[J].强激光与粒子束,2012,24(11):2768-2772.

Xia Minghe, Ji Ce, Wang Yujuan, et al. Operation models and waveform shaping of primary test stand[J]. High Power Laser and Particle Beams, 2012,24(11):2768-2772.

[15] 阚明先,王刚华,赵海龙,等.金属电阻率模型[J].爆炸与冲击,2013,33(3):282-286.

Kan Mingxian, Wang Ganghua, Zhao Hailong, et al. Electrical resistivity model for metals[J]. Explosion and Shock Waves, 2013,33(3):282-286.

Abstract: In the shot PTS-151 experiments the maximum velocity measured on the magnetically driven aluminum flyer plate with a thickness of 370 μm was 18 km/s, while that with a thickness 482 μm was 19 km/s. In this work, the data from the shot PTS-151 experiments on PTS were simulated and analyzed using the two dimensional magneto-hydro dynamics code MDSC2. The numerical simulation shows that the meaning of the maximum velocity measured in the shot PTS-151 should be different from that of the maximum velocity as reported in the related literatures where, as the free surface of the flyer plate was not ablated during the experiment, the maximum velocity measured was the flyer plate’s free surface velocity. In the shot PTS-151 experiments the free surface was ablated in the measurement of the two flyer plates, and therefore the maximum velocity measured by VISAR was the velocity of the last solid surface inside them just before they were totally ablated. In our simulation, if the initial free surface is not ablated, the maximum initial free surface velocity calculated is 7 km/s with the 370 μm thick flyer plate and 11.8 km/s with the 482 μm thick flyer plate, far below the velocity actually measured in the shot PTS-151 experiments. A new flyer plate was re-designed on the basis of the current condition of the shot PTS-151, with 680 μm as the optimal thickness, which would both prevent the free surface from ablation and achieve the maximum velocity of 17.5 km/s.

Keywords: PTS accelerator; magnetically driven flyer plate; two dimensional magnetically driven simulation code; solid reflecting surface; free surface velocity

(责任编辑 丁 峰)

Numericalanalysisandredesignofmagneticallydrivenaluminumflyerplate
onPTSaccelerator

Kan Mingxian, Yang Long, Duan Shuchao, Wang Ganghua, Xiao Bo, Zhang Zhaohui, Wang Guilin

(InstituteofFluidPhysics,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China)

中国工程物理研究院科学技术发展基金项目(2015B0201023)

O361.3国标学科代码1302547

A

10.11883/1001-1455(2017)05-0793-06

2016-01-29；

2016-05-17

国家自然科学基金项目(11405167,11571293);

阚明先(1971— )，男，硕士，副研究员，kanmx@caep.cn。