儿童早期执行功能与数学能力的关系：一项元分析

张亚杰，胡恩慧

（河南大学教育学部，河南开封 475004）

一、引言

执行功能是一种一般性的高级认知能力，对个体发展有非常重要的作用，它通过对各种认知过程进行协调和控制，以确保认知系统以灵活、优化的方式实现特定目标［1-2］。而数学能力作为一种技能表现，它的形成需要一定的认知基础。执行功能通过为儿童数学学习提供认知基础，并参与数学问题的解决过程对数学能力的发展提供一定的支持［2］。可见，执行功能与数学能力的关系非常紧密。同时，大量研究表明，执行功能与儿童早期数学能力显著相关，能够解释儿童早期数学能力发展的个体差异和后期的数学能力水平［3-6］。因此，关注儿童早期执行功能对数学能力发展的作用具有重要意义。

然而，大多数元分析文章只研究了特定的执行功能成分与数学技能之间的关系，没有说明所选取的相关系数r 是否由同一时间测量的非实验后测的数据计算得来，也没有对所选取的相关系数类型进行说明，如是否采用零级相关系数［7-11］。因此，本研究将对国内外探究执行功能及其三个子成分与数学能力关系的实证研究进行元分析，纳入由非实验后测的横向测量数据得来的零级相关系数结果作为效应值，尽最大能力保证研究的客观性、全面性以及可推广性。

此外，国内外儿童早期执行功能与数学能力的相关关系结果并不一致。这或许与儿童早期执行功能与数学能力水平之间的关系会受到其他因素的影响有关。元分析具有相对客观地得出一般性的结论以解决研究争议、深入探究引起研究结果差异的原因的优势［12］。因此本研究将采用元分析方法，以2019年以来的国内外探究执行功能与数学能力关系的实证研究为研究对象，探讨执行功能及子成分与数学能力及子成分的相关程度，分析样本来源、年龄、性别等变量对二者关系的调节作用，以期丰富儿童早期执行功能与数学能力关系的研究图谱，为未来的研究提供更好的视角和方向。

（一）执行功能的结构

执行功能（executive function，简称EF）是指个体自我控制或自我调节所需的高级认知能力，包括工作记忆更新、认知灵活性（又称“定势转换”或“转换”）以及抑制控制三个方面的内容［13］。工作记忆（working memory，简称WM）是通过语音回路、视觉空间画板和中央执行系统，暂时储存和操作一些复杂任务的容量有限的系统［14-15］。然而工作记忆更新需要对相关信息进行主动操作，而不是仅仅充当短期存储工具［13］。更新偏重于从工作记忆中删除过时的项目、添加新项目，或者修改现有的所有或部分项目。因素分析结果显示，更新和传统工作记忆成分有很大重叠［16］。因此，本研究中的工作记忆既包括执行功能中的更新成分，又包括传统工作记忆成分。认知灵活性（cognitive flexibility，简称CF）是指在任务或心理定势之间灵活转换的能力。抑制控制（inhibitory control，简称IC）是有意压制主导或优势反应的能力［17］。具体测查任务见表1 编码系统。

表1 编码系统表

（二）数学能力的内容与测量

目前，学界对于儿童数学能力的定义尚不一致。国内学者罗丽红和杨宁将数学能力定义为数字读写、掌握数字事实、掌握运算技能、理解数学概念等四种能力［18］。孙瑾则认为学前儿童数学能力包含正式数学能力和非正式数学能力两种［19］。正式数学能力指儿童在学校教育体系中发展的数学能力；而非正式数学能力则是儿童在日常生活中建构的一种基本数学能力，对于儿童整体数学能力的发展具有重要作用［19］。而李莉等人则认为数学学习包含集合与模式、数概念、数运算、几何与空间、测量等五个方面［7］。

此外，全美数学教师协会将儿童的数学能力划分为内容性数学能力和过程性数学能力［20］。内容性数学能力是指儿童掌握计数、简单符号表征及简单运算等基本数学内容的能力。过程性数学能力是指儿童在学习和理解数学知识的基础上，运用数学知识解决实际问题的能力［21］。而《3～6 岁儿童学习与发展指南》中的科学领域提出了三个数学认知目标：初步感知生活中数学的有用和有趣；感知和理解数、量及数量关系；感知形状与空间关系。综上，本研究中的数学能力定义采用李莉等人的解释，即数学能力主要包括集合与模式（SP）、数概念（NC）、数运算（NO）、几何与空间（GS）以及测量（M）五个方面［7］。具体测查任务见表1编码系统。

（三）执行功能与数学能力的关系

虽然近年来国内外有关儿童早期执行功能与数学能力发展的关系研究众多，但是其相关结果并不一致。有研究认为执行功能与儿童数学能力具有显著中高度正相关关系［22］，这可能是由于执行功能和数学能力存在着共同的生理基础和相似的认知过程［2］。然而，也有研究发现执行功能与数学能力呈显著低度相关关系［23］。甚至，还有研究发现执行功能与数运算的相关程度非常微弱［24］。这可能是由于研究对象的年龄和使用的测查任务不同导致的。

具体而言，在工作记忆方面，有研究者发现工作记忆与5 岁幼儿的数学能力呈显著相关关系［25］。另有研究发现工作记忆与儿童的数学能力呈低度相关关系［26］。然而，Georgiou 等人在对平均年龄为6.41 岁的加拿大儿童测查后发现，工作记忆与儿童的数概念能力呈负相关关系［27］。在认知灵活性方面，有研究认为认知灵活性与儿童数学能力呈显著中度相关［28］。然而，宋思涵的研究却发现认知灵活性与儿童的数感呈显著低度相关关系［29］。在抑制控制方面，刘小龙的研究发现学前儿童的抑制控制与数学能力呈显著中度相关关系［2］。然而张利的研究却发现抑制控制与儿童的数学能力只有低度相关［30］。此外，Bonifacci 等人的研究发现抑制控制与数学能力仅有非常微弱的相关［31］。

综上，研究者们对于执行功能与儿童早期数学能力水平之间的关系探讨仍存在争议。但经过整理和分析后发现，大多数研究都认为执行功能及其子成分与数学能力呈显著相关关系。此外，由于探究执行功能子成分与数学能力关系的实证研究样本量大小不同，不同执行功能子成分对儿童数学能力的贡献不同，可能会使得执行功能子成分与数学能力的相关程度不同。因此，本研究提出假设1：执行功能与儿童早期数学能力之间呈显著相关关系，不同执行功能子成分与数学能力的相关程度不同。

（四）执行功能与数学能力关系的调节变量

研究表明，不同国家和地区的儿童解决数学问题的速度和策略使用存在差异，且在问题解决时表现出不同的工作记忆资源需求状况。这可能是由于不同的小学教学方法、数字语言以及非正式的文化规范和标准导致的［32］。此外，Tang 等人的研究发现，母语为汉语者和母语为英语者在处理数字时的大脑表征不同，而这可能影响短时记忆能力［33］。同时，Friso-van den Bos 等人的研究发现样本的原籍国对认知灵活性和数学成绩之间的相关性有调节作用［34］。因此，提出假设2：样本来源对执行功能与数学能力的相关关系存在调节作用，来自不同国家或地区儿童的执行功能与数学能力关系可能会存在差别。

已有研究发现，年龄能够调节3～6 岁幼儿工作记忆、认知灵活性与早期数运算能力的关系［35］。Geary 对小学一年级到五年级幼儿的执行功能和运算能力进行测查后发现工作记忆对于运算能力的影响随年级递增［36］。而Friso-van den Bos 等人发现认知灵活性和数学技能之间的关系在年幼的儿童中比在年长的儿童中更强［34］。综上，年龄可能会调节执行功能和儿童早期数学能力之间的关系。因此，提出假设3：年龄对执行功能与数学能力关系的相关关系存在调节作用，不同年龄儿童的执行功能与数学能力关系也可能会存在差别。

Jordan 等人的研究发现，儿童数学能力发展的性别差异从5-6 岁就开始出现，男孩的数学表现更好［37］。在之前Jordan 等人对学龄儿童的研究中也报告了相似的性别效应［38］。此外，在对6-12 岁儿童的元分析中，Pascual 等人发现，性别显著调节了更新、总体执行功能与数学成绩的关系［39］。同时，Zhong 等人的元分析研究也表明，学前儿童的性别能够调节执行功能与数学能力之间的关系［11］。因此，提出假设4：性别对执行功能与数学能力关系的相关关系存在调节作用。

二、研究设计

（一）研究方法与工具

本研究通过提取有关文献的样本量、研究工具、变量关系及相关系数等，对执行功能三个主成分及总分和数学能力之间的变量关系进行分类，以二者的皮尔逊相关系数r作为效应值，探究执行功能和数学能力之间的实际关系以及样本来源、年龄、性别对儿童早期执行功能与数学能力相关程度的调节作用。此外，本研究使用End-Note 20 导入并筛选文献；同时运用Execl 2019 进行数据编码；最后使用CMA 3.3（Comprehensive Meta-Analysis）进行数据分析。

（二）研究过程

1.文献检索

首先，结合本研究的目的，在正式检索相关文献之前，制定文献检索标准。本研究的文献检索标准为：（1）文献研究内容为执行功能与数学能力的关系；（2）语种分别为中文和英文；（3）发表时间为2019 年～2023 年，文献检索时间截止到2023 年3 月2 日。为了考察国内外最新相关研究成果，因而对2019 年来的文献进行检索。其次，正式检索文献。英文文献检索主要使用Web of Science 核心合集、EBSCO-ERIC、ScienceDirect、PQDT、Wiley 期刊全文数据库等进行检索，其中执行功能以“executive function”为关键词；工作记忆或更新以“working memory”“updating”为关键词；认知灵活性或任务转换以“cognitive flexibility”“shifting”“set shifting”“task-switching”为 关键词；抑制控制以“inhibition”“inhibitory control”“inhibition control”“inhibiting ability”为关键词；数学能力以“math/number/mathematical/numerical/arithmetic+competence”“math/number/mathematical/numerical/arithmetic+ability”“math/number/mat hematical/numerical/arithmetic+achievement”“math/number/mathematical/numerical/arithmetic+performance”“math/number/mathematical/numerical/arith metic+skill”“math/number/mathematical/numerical/arithmetic+development”为关键词；3～8 岁儿童以“children”“kids”“preschool children”“elementary school children”为关键词。中文文献检索主要使用中国知网数据库、维普期刊网、万方数据库等进行检索，其中执行功能及其三个主成分以“执行功能、工作记忆、更新、认知灵活性、任务转换、抑制控制”为关键词；数学能力以“数学能力、数学成绩、数学表现”为关键词；3～8 岁儿童以“幼儿、学前儿童、小学低年级”为关键词。此外，为了避免遗漏和保证文献的查全率，对已检索到的文献中的引文进行文献补查和补充。首次检索获得的文献数量为2421篇。

2.文献筛选

根据检索词进行检索和对已检索到的文献中的引文进行文献回溯之后，共得到2260篇外文文献和51 篇中文文献。依据本研究的目的和研究内容，确定文献纳入标准为：（1）必须为量化研究，排除理论探讨、质性研究及文献综述。（2）必须详细报告执行功能和数学能力的测查内容及任务，不可包含教师评定法。（3）必须报告由同一时间测量的且为非实验后测的执行功能和数学能力数据计算而来的零阶相关系数r。因为偏相关结果不能纯粹代表执行功能与数学能力之间的关系，不等同于零级相关［40］。（4）样本年龄范围需在3～8 岁。国际一般认定儿童早期的概念为0～8岁［41］。但由于3岁前婴幼儿身心发展速度较快，尤其是与执行功能和数学能力发展有关的大脑发育较快，稳定性不强。因此，本研究将儿童早期定义为3～8 岁。（5）样本需为正常群体，不含数困、学困或残障儿童。本研究以正常儿童为样本，排除特殊群体，探究正常儿童执行功能与数学能力的关系及影响二者关系的因素。（6）文献发表时间为2019～2023 年，但部分研究基于早期数据库进行分析，数据收集年份和文章发表年份存在较大出入，对此类情况，本研究仅提取数据收集年份。（7）数据重复发表的研究仅取其中效应值报告最完整的研究。运用EndNote 20文献管理软件，最终筛选出32 篇外文文献和10 篇中文文献。文献筛选流程图见图1。

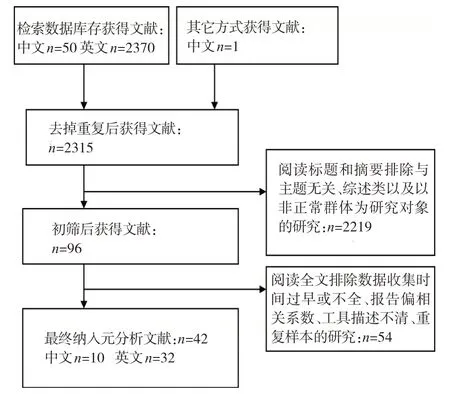
图1 文献筛选流程图

3.文献编码

对纳入的文献信息进行编码，所编码的特征包括：作者及发表时间、样本来源、文献来源、样本量、男生比、平均年龄、执行功能和数学能力变量关系、相关系数、文献质量分数。为保证编码效度，编码由两位评分者独立完成，最终计算编码一致性为95.9%。若编码不一致，则通过查看原始文献，讨论更正。本研究的编码系统表见表1。

编码结果显示：（1）本研究共纳入原始研究42 项（其中一项包含中国、加拿大两国样本）。详细信息见表2。（2）期刊论文35 篇，学位论文7篇。（3）样本总量为12495 名儿童。其中，最大样本量为1868 人，最小样本量为43 人。（4）样本来源分布：欧洲13项，美洲6项，亚洲24项。（5）样本平均年龄范围：3.62 岁～8 岁。本研究将儿童早期年龄定义为3～8 岁，包括学前儿童阶段（3～6 岁）和小学低年级阶段（6～8 岁）。因此，将样本平均年龄在3～6岁之内的研究编码为1，将平均年龄在6～8岁之内的编码为2，纳入调节效应分析。

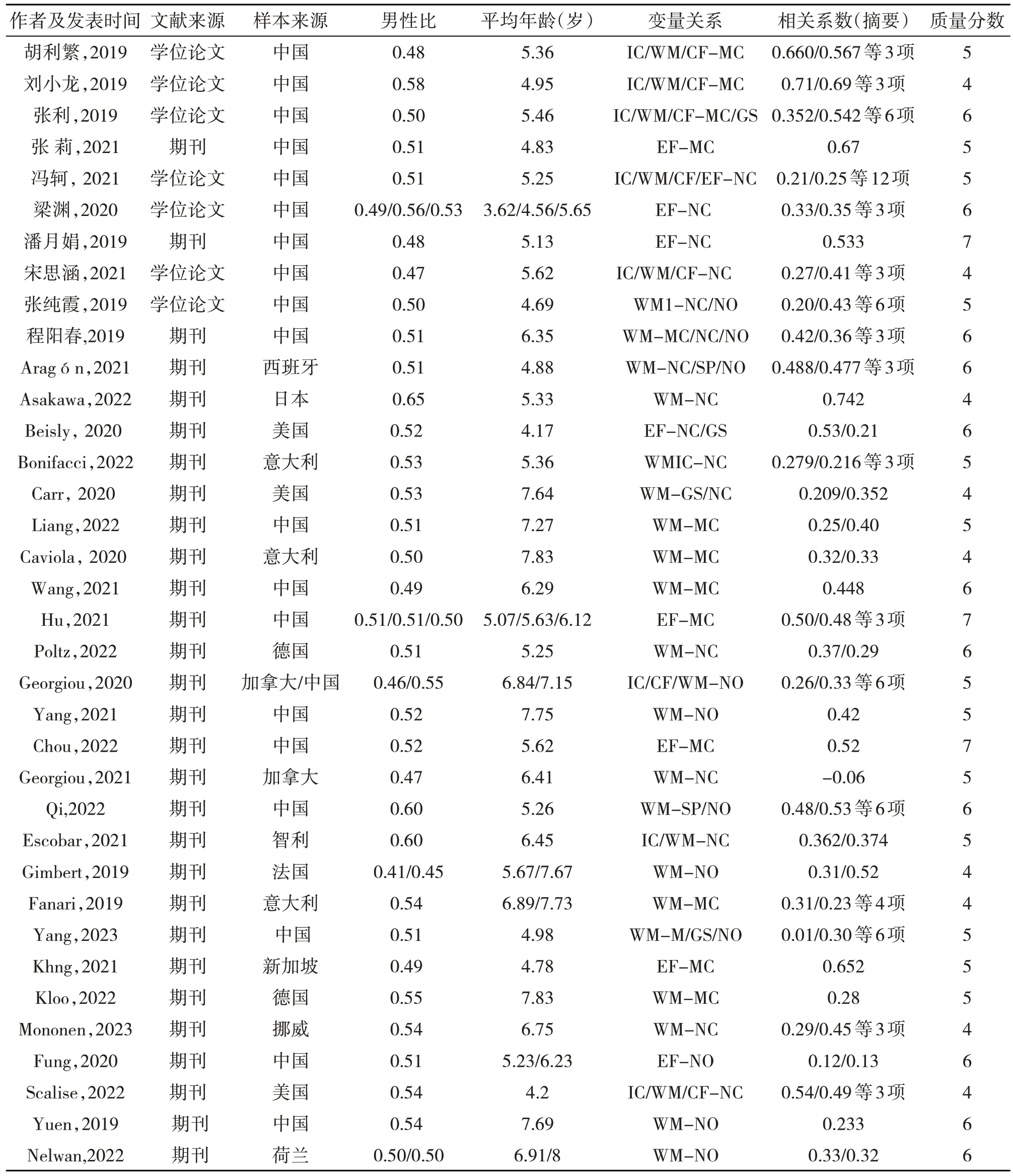
表2 纳入分析的原始研究基本信息表

4.质量评价

参考张亚利等人编制的元分析文献质量评价量表对所选文献进行质量评价［42］。该量表的评价标准共四点：被试的选取、数据有效率、测量工具的信度、刊物级别。总得分为文献质量分数，介于0～8 之间，分数越高，说明文献质量越高。由表2 可得，文献质量评价分数均值为5.1，仅有1 项研究的质量评价分数低于理论中值4，文献整体质量良好［43］。

5.效应值提取

本研究效应值提取方法如下：（1）选取皮尔逊零阶相关系数r 作为效应值指标，排除偏相关系数。（2）本研究选取的效应值包括执行功能（EF）/工作记忆（WM）/抑制控制（IC）/认知灵活性（CF）与数学能力总分（T）/集合与模式（SP）/数概念（NC）/数运算（NO）/几何与空间（GS）/测量（M）的相关系数。（3）同一研究中报告了不同年龄儿童的测查结果时，仅选取测查时间在3～8 岁时的结果，排除其它测查时间段的研究结果。（4）若原始研究为实验研究，报告前测、后测结果，仅选取前测结果。（5）若原始研究为纵向研究设计，则仅选取由同一时间段内测查的执行功能和数学能力数据分析而来的相关系数作为效应值。排除纵向相关系数。（6）原始研究中所报告的相关系数均采纳为效应值，无遗漏之处。依据上述方法，最终获取120 项效应值。执行功能和数学能力效应值数量分布情况见表3。

表3 执行功能和数学能力效应值数量分布表

6.数据分析

根据研究目的和编码数据情况，本研究的数据分析主要分为两个方面：（1）主效应检验，即检验执行功能与儿童早期数学能力的关系。主效应检验分为两级：一级主效应检验，即对EF 与T/SP/NC/NO/GS/M 等总体数学能力及子变量之间的相关分析；二级主效应检验包括WM/IC/CF 等执行功能子成分与总体数学能力及子变量（同上）之间的相关分析。（2）调节效应检验，即检验样本来源、儿童年龄、性别对执行功能与数学能力相关关系的调节作用。

三、研究结果

（一）主效应检验

1.执行功能与数学能力的关系

（1）效应值分布及异质性检验

根据数据提取结果，执行功能EF与数学能力总分及子变量相关系数结果共20 项。其中EF 与数学能力总分T 和NC 的相关系数结果分别为9项和8 项；与NO 和GS 的相关系数结果为2 项和1项；与SP 和M 的相关系数结果皆为0 项。对总体效应值进行异质性Q检验和I2检验发现，各效应值之间存在显著差异。结果显示，Q=264.305，I2=92.811%，p=0.000 ＜0.001。所选文章的效应值之间存在显著的高异质性，因此，此次元分析采用随机效应模型。

（2）发表偏倚检验

本研究采用漏斗图、Egger检验以及Rosenthal失安全系数检验所纳入分析的原始文献是否存在发表偏倚。从漏斗图中可以看出，大部分独立效应值都集中在图形上方，且聚集在平均效应值附近；Egger线性回归结果表明，p=0.12 ＞0.05；失安全系数为7664，当失安全系数大于5k+10（k=20）时，发表偏倚出现的可能性较小。综上，此次元分析存在出版偏误的可能性较小。

（3）EF与数学能力的关系

元分析结果显示，执行功能与以上所有不同方面数学能力的总效应值为0.472（置信区间未包含0，且p＜0.001），二者相关关系显著。根据Gignac 和Szodorai 的建议［44］，r=0.472 ＞0.4，EF 与数学能力的关系为显著高度相关。此外，由于EF与NO、GS、SP 及M 的相关系数结果太少，而不将上述四类相关系数结果纳入元分析，仅以EF与NC、T的相关结果纳入元分析。结果发现，EF与NC、T存在显著高度相关（r（EF-NC）=0.518；r（EF-T）=0.519。置信区间均不包含0，且p＜0.001）。

2.工作记忆与数学能力的关系

（1）效应值分布及异质性检验

根据数据提取结果，WM 与数学能力总分及子变量的相关系数结果共75 项。其中WM 与T、NC 及NO 的相关系数结果分别为18 项、25 项及22 项；而与SP、GS、M 的相关系数结果分别为4项、4 项及2 项。对总体效应值进行异质性Q检验和I2检验发现，各效应值之间存在显著差异。结果显示，Q=357.379，I2=79.294%，p=0.000 ＜0.001。所选取文章的效应值之间存在显著的高异质性，因此，此次元分析采用随机效应模型。

（2）发表偏倚检验

从漏斗图中可以看出，大部分独立效应值都集中在图形上方，且聚集在平均效应值附近；Egger 线性回归结果表明，p=0.15 ＞0.05；失安全系数为2792，当失安全系数大于5k+10（k=75）时，发表偏倚出现的可能性较小。因而，可以判断出此次元分析存在出版偏误的可能性较小。

（3）WM与数学能力的关系

元分析结果显示，工作记忆与以上所有不同方面数学能力的总效应值为0.357（置信区间未包含0，且p＜0.001）。这表明WM 与数学能力的关系为显著中度相关。此外，由于WM 与SP、GS、M的相关系数结果太少，而不将其相关系数结果纳入元分析，仅以WM 与T、NC 及NO 的相关结果纳入元分析。结果发现，WM 与NC的相关程度强于WM 与NO 的相关程度（r（WM-NC）=0.350；r（WM-NO）=0.337。置信区间均不包含0，且p＜0.001）

3.认知灵活性与数学能力的关系

（1）效应值分布及异质性检验

根据数据提取结果，CF与数学能力总分及子变量的相关系数结果共11 项。其中CF 与NC 的相关系数结果为5 项；与T、NO、GS、SP、M 的相关系数结果分别为3项、2项、1项、0项及0项。对总体效应值进行异质性Q检验和I2检验发现，各效应值之间存在显著差异。结果显示，Q=104.507，I2=90.431%，p=0.000＜0.001。所选文章的效应值之间存在显著的高异质性，因此，此次元分析采用随机效应模型。

（2）发表偏倚检验

从漏斗图中可以看出，大部分独立效应值都集中在图形上方，且聚集在平均效应值附近；Egger 线性回归结果表明，p=0.08＞0.05；失安全系数为791，当失安全系数大于5k+10（k=11）时，发表偏倚出现的可能性较小。因而，可以判断出此次元分析存在出版偏误的可能性较小。

（3）CF与数学能力的关系

元分析结果显示，CF 与以上所有不同方面数学能力的总效应值为0.413（置信区间未包含0，且p＜0.001）。这表明CF 与数学能力的关系为显著高度相关。此外，由于CF 与T、NO、GS、SP、M 的相关系数结果太少，而不将其相关系数结果纳入元分析，仅以CF 与NC 的相关结果纳入元分析。结果发现，CF 与NC 存在显著高度相关（r（CF-NC）=0.486；置信区间不包含0，且p＜0.001）。

4.抑制控制与数学能力的关系

（1）效应值分布及异质性检验

根据数据提取结果，IC 与数学能力总分及子变量的相关系数结果共14 项。其中IC 与NC 的相关结果有7 项；而与T、NO、GS、SP、M 的相关结果分别有4项、2项、1项、0项及0项。对总体效应值进行异质性Q检验和I2检验发现，各效应值之间存在显著差异。结果显示，Q=134.419，I2=90.329%，p=0.000 ＜0.001。所选文章的效应值之间存在显著的高异质性，因此，此次元分析采用随机效应模型。

（2）发表偏倚检验

从漏斗图中可以看出，大部分独立效应值都集中在图形中上方，且聚集在平均效应值附近；Egger线性回归结果表明，p=0.053 ＞0.05；失安全系数为1066，当失安全系数大于5k+10（k=14）时，发表偏倚出现的可能性较小。因而，可以判断出此次元分析存在出版偏误的可能性较小。

（3）IC与数学能力的关系

元分析结果显示，元分析结果显示，IC 与以上所有不同方面数学能力的总效应值为0.382（置信区间未包含0，且p＜0.001）。这表明IC 与数学能力的关系为显著中度相关。此外，由于IC与T、NO、GS、SP、M 的相关系数结果太少，而不将其相关系数结果纳入元分析，仅以IC 与NC 的相关结果纳入元分析。结果发现，IC 与NC 存在显著近高度相关（r（IC-NC）=0.394；置信区间不包含0，且p＜0.001）。

（二）调节效应检验

1.样本来源

将EF 与数学能力的相关系数结果根据样本来源分成3 个亚组，各亚组的相关系数分别是2 项、2 项 及16 项。CF 与数学能 力的3 个 亚组的相关系数分别是0 项、2 项及9 项。此外，IC 与数学能力的3 个亚组的相关系数分别是1项、3 项及10 项。根据元分析中亚组分析原则，即各亚组有4 个及以上的独立效应值时才纳入亚组分析［45］。以上EF、CF、IC 与数学能力分成亚组后的相关系数个数由于不满足各亚组均为4 个及以上的条件，不纳入分析。因此，仅进行样本来源对WM 与数学能力相关关系的调节效应分析。亚组分析结果显示：样本来源能够显著调节WM 与数学能力的关系，其Q值（组间）为6.588，p＜0.05。WM 与数学能力在亚洲的三个国家中的相关系数要大于在美洲和欧洲的国家。具体信息见表4。

表4 样本来源对WM与数学能力关系的调节效应

2.年龄

将EF 与数学能力的相关系数结果根据年龄阶段分成2 个亚组，各亚组的相关系数分别是3项和17 项。CF 与数学能力的2 个亚组的相关系数分别是2项和9项。此外，IC与数学能力的2个亚组的相关系数分别是3 项和11 项。以上EF、CF、IC 与数学能力分成亚组后的相关系数个数由于不满足各亚组均为4 个及以上的条件，故不纳入分析。因此，仅进行年龄阶段对WM 与数学能力相关关系的调节效应分析。亚组分析结果显示：不同年龄阶段能够显著调节WM 与数学能力的关系，其Q值（组间）为14.366，p＜0.001。WM与数学能力在3～6岁儿童中的相关系数要高于在6～8岁儿童中。具体信息见表5。

表5 不同年龄阶段对WM与数学能力关系的调节效应

3.性别

利用元回归分析的方法检验男性比对执行功能与数学能力的相关关系是否有显著影响，结果发现：性别能够极其显著地调节WM 与数学能力之间的关系（p=0.0006）。但是性别对EF、CF、IC 与数学能力关系的调节作用不显著（p=0.322;p=0.837;p=0.617）。

四、讨论

近年来有很多研究都报告了执行功能与数学能力的关系，但是这些相关结果之间却存在很大的不一致。本研究运用元分析方法旨在探讨：（1）儿童早期执行功能及子成分与数学能力之间的相关程度和差异性。（2）样本来源、年龄、性别对执行功能及其子成分与数学能力关系的调节作用。

（一）执行功能及其子成分与数学能力的关系

元分析结果支持假设1，即儿童早期执行功能及子成分与数学能力之间呈显著相关关系，且相关程度不同。具体相关结果如下：r（EF）（0.472）＞r（CF）（0.413）＞r（IC）（0.382）＞r（WM）（0.357）。这表明执行功能与数学能力的相关程度最高，其次为CF 与数学能力的相关，再次为IC与数学能力的相关，最后为WM 与数学能力的相关。

本研究发现认知灵活性与数学能力的关系强于抑制控制、工作记忆与数学能力的关系，且工作记忆与数学能力的相关关系最弱。这与Friso-van den Bos 等人和Zhong 等人的研究结果不同，这两项研究发现工作记忆与数学技能的相关关系最强［11，34］，抑制控制和认知灵活性与数学技能的相关关系相对较弱。这种不一致可能是由以下三个原因导致的：一是，研究纳入的原始研究考察的数学能力范式不一致，是单独考察某一方面的数学能力代表一般数学能力还是考察总体数学能力代表一般数学能力存在差异；二是，研究涉及的原始研究的研究工具不同；三是，研究所选取的效应量多少不同。以上原因可能会使得元分析结果不一致。

1.执行功能与数学能力的关系

研究发现EF 与数学能力存在显著高度正相关关系，与儿童的数概念能力存在显著高度正相关关系。这同其他研究一样肯定了EF 与数学能力的显著相关关系［46］。EF 是儿童数学能力和推理能力发展的前提条件和基础［47］，它还可以提高儿童的自我调节能力，影响儿童与其他人的互动，从而直接或间接地影响儿童的数学学习［48］，并且幼儿时期的执行功能可以预测正式入学后数学成绩［49］。Zhong 等人与Emslander 和Scherer的元分析研究也发现，EF与数学能力呈显著相关关系［11，50］。

2.工作记忆与数学能力的关系

研究发现WM与数学能力存在显著中度正相关关系，与儿童的数概念能力和数运算能力存在显著中度正相关关系。工作记忆在儿童数学学习中不仅起到保持信息的作用，也起到操作和更新信息的作用。而就是这种操作和更新工作记忆信息的能力，而非简单维护信息的能力，似乎对数学熟练程度至关重要［51］。大量研究表明，工作记忆与数学能力关系密切［52］。Passolunghi等人的研究表明工作记忆和计数能力是儿童早期数学学习最有效的前驱物［53］。此外，研究者们发现视觉工作记忆对儿童早期数学学习的发展尤其重要。Bull 等人的研究表明视觉空间短期记忆广度是预测数学能力的特别指标。相关和回归分析显示，视觉短期记忆和工作记忆在每个时间点上都能预测数学成绩［6］。同时，李莉等人还发现儿童的中央执行能力对整个数学学习都很重要［7］。而语音环路支持言语理解和获得，可以让儿童理解数字的言语指导［54］。因此，工作记忆能够帮助儿童的数学学习。

3.认知灵活性与数学能力的关系

研究发现认知灵活性与数学能力存在显著高度正相关关系，与儿童的数概念能力存在显著高度正相关关系。最近的研究表明认知灵活性水平越高的孩子在基本数字技能的问题上和对数字的理解上表现得越好［55］。这可能是因为更高的转换能力有助于儿童在不同的数学策略之间进行转换，以解决问题或理解概念［8］。Cragg 和Chevalier 也指出CF 参与了寻找解决问题的创造性替代方案的过程，因为它涉及创造和选择创新性的工作策略［56］。两项元分析研究也表明，儿童转换能力与数学能力显著相关［9-10］。

4.抑制控制与数学能力的关系

研究发现抑制控制与数学能力存在显著中度正相关关系，与儿童的数概念能力存在显著近高度正相关关系。Aydmune等人认为抑制控制是一种自发的认知行为，其在复杂的认知目标过程中具有重要作用［57］。儿童在解决数学问题时，通过抑制控制排除无关信息的干扰，将注意力中于解决问题的关键信息，正确认知相关信息，从而采取正确的策略解决问题。因而，儿童的抑制控制与数学能力关系密切，抑制控制能够预测之后数学能力的发展［58］。抑制控制差是造成儿童解决计算问题困难的最基本原因之一［59］。可见，抑制控制是儿童早期数学能力的重要影响因素。

（二）调节变量的影响

1.样本来源的调节作用

研究发现样本来源能够显著调节WM 与数学能力的关系，并且亚洲国家中的WM 与数学能力的关系要比美洲国家和欧洲国家中的关系更加密切。这一发现在一定程度上验证了Emslander 和Scherer 的研究，他们发现样本的来源国家和所在洲能够调节6 岁11 个月以下儿童的EF与数学智力的关系［50］。这可能是由于不同国家和文化下的教师使用的教学方法不同或儿童使用的数学问题解决策略不同而导致的。但是，Friso-van den Bos 等人在一项针对4～12岁儿童的元分析研究中发现，国籍对数学成绩和工作记忆之间的相关性没有任何影响［34］。造成这种差异的原因可能有两个：一是，所纳入原始研究的样本年龄不同；二是测量工具或任务有所不同。值得注意的是，在目前的调节效应分析中，一共包含75项WM 与数学能力的相关结果。其中，有29项来自欧洲等国家的儿童，有40项来自亚洲等国家的儿童，而仅有6 项来自美洲。这可能在一定程度上限制了所得出的关于国家和大陆会影响WM 与数学能力关系的推论。因此，需谨慎对待此次推论。

2.年龄的调节作用

研究发现年龄能够显著调节WM 与数学能力的关系，并且3～6 岁儿童的WM 与数学能力关系要比6～8 岁儿童的更为密切。这在一定程度肯定了Friso-van den Bos 等人和李莉等人的研究［7，34］，因为他们的研究仅证实了年龄可以调节部分工作记忆成分和数学能力的关系。以往研究表明儿童早期工作记忆的各成分随年龄变化的发展特点不同。张纯霞的研究还发现儿童的语音环路在5 岁时快速发展，而中央执行在4～5岁时快速发展。同时，她的研究也表明工作记忆各成分对数学能力的影响会随着年龄发生变化［26］。Fuchs 等人的研究发现，中央执行是协调年幼儿童数数策略的关键，而较少参与年长儿童的事实提取［60］。Raghubar 等人的研究发现，随着年龄的增长，数学成绩与视觉空间画板的相关程度会下降，因为增加了对语音循环的依赖［61］。这些研究表明在3～6 岁时期，儿童的工作记忆各方面的能力都与数学能力的关系极为密切。

3.性别的调节作用

研究发现性别能够极其显著地调节WM 与数学能力之间的关系，但是性别对EF、CF、IC 与数学能力关系的调节作用不显著。Zhong 等人的元分析研究发现性别能够调节EF 与数学能力的关系［11］；而Emslander 和Scherer 等人的元分析却发现性别不能调节EF 与数学能力的关系［50］。Pascual 等人发现，性别显著调节了更新与数学成绩的关系［39］。以上元分析结果不尽相同，这可能是由以下两个原因导致的：一是，样本年龄范围不一致；二是，纳入分析的效应值的多少不一致。此外，由于本研究中EF与数学能力的相关结果有20 项，而CF、IC 与数学能力的相关结果各有10 项左右，EF、CF、IC 与数学能力的相关结果相对较少，这可能会影响调节效应检验结果。

（三）局限与展望

本研究通过元分析的方法探究了儿童早期执行功能与数学能力的关系，探讨了样本来源、年龄、性别对二者关系的调节作用，从而澄清了有关研究中执行功能与数学能力相关强度和方向不一致的问题，发现了影响和调节二者关系的因素。然而，本研究也存在不足之处：第一，本研究仅关注了执行功能和数学能力的横向相关结果，只能揭示二者之间的相关关系，而不能很好的揭示因果关系。第二，本研究仅关注了以身心发展正常儿童为样本的相关研究，未关注身心发展障碍儿童的执行功能和数学能力发展情况，如数困儿童、ADHD 儿童等。这可能会导致研究没有包含到所有可能的早期阶段儿童样本。

对未来研究的展望：首先，本研究在探究执行功能与数学能力关系的过程中发现，近年来关于数学能力的研究大多集中在数概念和数运算上，而对空间与几何、测量等方面的关注较少。未来的研究应对空间与几何和测量等研究内容加以重视。其次，关于执行功能的研究大多集中在工作记忆上，而关于认知灵活性和抑制控制的研究则较少。未来应重视认知灵活性和抑制控制的相关研究。再次，为了更好地揭示执行功能与数学能力之间的因果关系，未来可以增加实验干预研究和长期跟踪研究。最后，为了使得元分析研究更加具有科学性、完整性及可推广性，可以加强对身心发展障碍儿童的执行功能与数学能力关系的研究，以揭示相关规律、提出对策建议。

五、结论

本研究采用元分析方法发现：儿童早期EF、CF 与数学能力存在高等程度的正相关，IC、WM与数学能力存在中等程度的正相关。样本来源、年龄及性别能够显著调节儿童早期WM 与数学能力的关系。性别对儿童早期EF、CF、IC 与数学能力关系的调节作用不显著。本研究的结论澄清了现有研究的争议，说明了儿童早期执行功能及其子成分与数学能力之间的真实联系，并为后续研究提供了一些参考。