生问引学:学习真实发生,思维切实提升
2023-12-25竺柏明童欣
竺柏明 童欣

[摘 要]人教版教材中的“分数与除法”是凭借两个“被除数小于除数”的例子归纳得出分数与除法的关系,但学生对此可能会产生疑问。为了促进学生深入思考,教师要鼓励学生提出他们内心的疑问,再借助疑问深入探究“被除数大于或等于除数”的情况。通过完全归纳的过程,学生能够深刻地构建知识体系,学习得以真实发生,思维得到切实提升。
[关键词]分数与除法;发现问题;提出问题;思维;推理
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2023)29-0002-04
【课前之思】
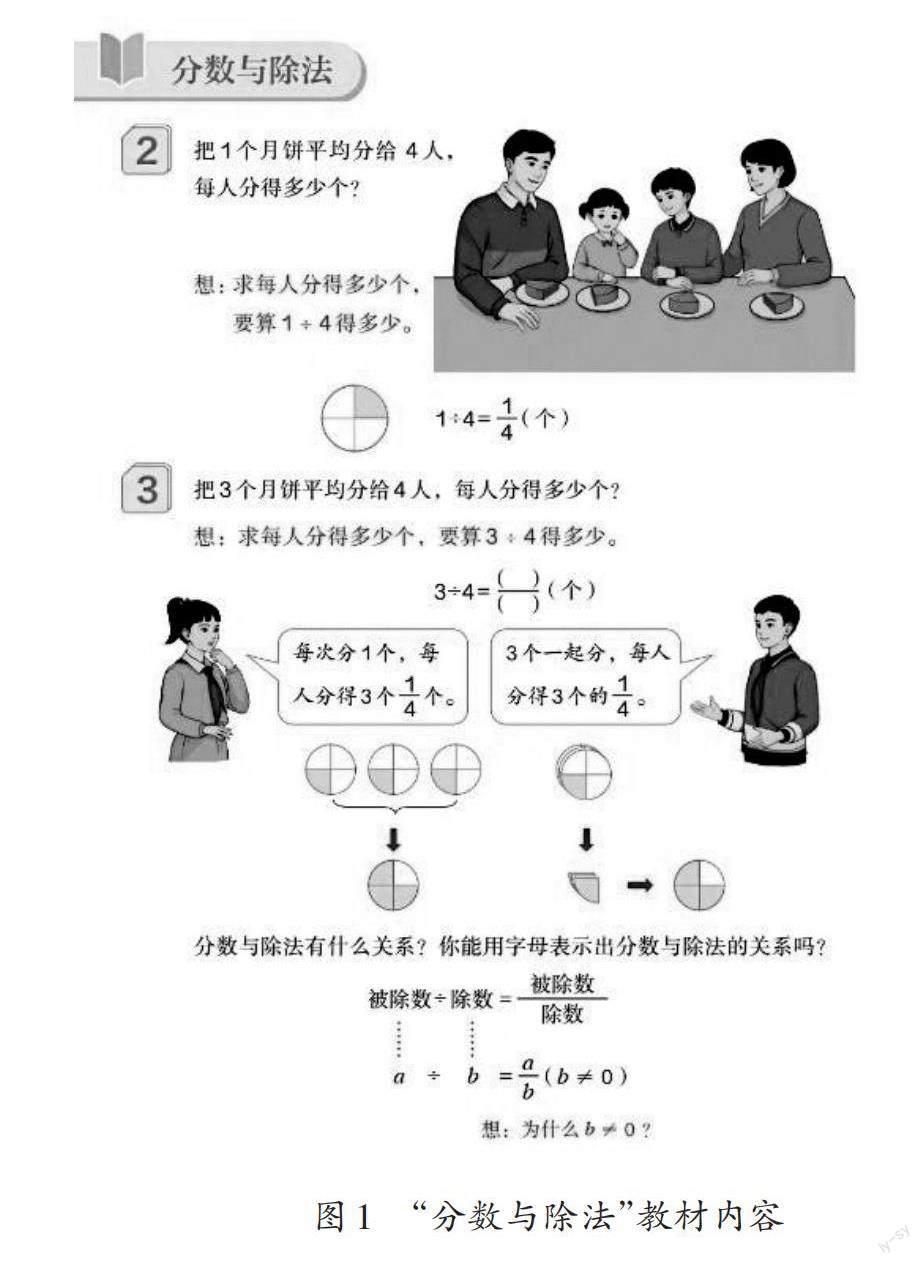
人教版教材将“分数与除法”编排在五年级下册。从教材呈现的内容(如图1)来看,本课是借助两个关于除法的实际问题,揭示分数与除法的关系,使學生不仅能理解分数表示部分与整体的关系(即“份数”定义),还能理解分数表示两个整数相除的商(即“商”定义),从而深化和扩展对分数意义的理解。
教材以1÷4=?和3÷4=?两道除法算式为例,得出分数与除法的关系。然而,这种方法在逻辑上存在一些不足之处,因为它仅考虑了被除数小于除数的情况,没有涵盖被除数大于或等于除数的情况。这种不完整的归纳可能会引发学生的疑问:“如果被除数大于除数,或者被除数和除数相等,会有什么结果呢?”需要指出的是,在之前的除法学习中,被除数大于除数的情况更为常见,因此,仅以不常见的被除数小于除数的情况来得出结论可能会引起学生的疑问。
根据新的课程理念,引导学生发现和提出有意义的数学问题是培养学生质疑精神和批判性思维的重要方式,这也是值得追求的数学课程目标。因此,笔者建议将学生提出的问题纳入教学中,以激发学生深入探究和全面归纳的兴趣。这将为他们提供发展推理意识的绝佳机会,而推理正是《义务教育数学课程标准(2022年版)》(以下简称《课程标准》)所强调的最重要的数学思维之一。
也许有人会担心,这样的教学是否会涉及假分数?(在人教版教材中,假分数通常会在后面的课程中介绍,而不是通过两数相除引入)笔者认为这种担忧是不必要的,因为《课程标准》鼓励教师“要整体分析数学内容本质和学生认知规律,合理整合教学内容”。假分数的本质是为了表示被除数大于除数时的商,而这节课正好介绍了两个整数相除的商可以用分数表示。因此,学生在学习过程中产生“被除数大于或等于除数时,商会如何表示”的疑问时,正是引入假分数的合适时机。(北师大版教材采用了先教假分数再教分数和除法的关系的顺序编排教学内容)
根据以上思考,笔者进行了多次尝试,最终制订了可行的教学方案。
【课堂实践】
一、课题引思,明确方向
1.揭示课题,引发疑问
师:一起来读一下课题。读完课题,你有什么疑问?
生1:分数是一种数,除法是一种运算,它们有关系吗?
生2:分数怎么会与除法有关系呢?
师:今天我们就来研究它们的关系。
2.生成素材,初步感知
师(引导学生回忆学过的分数和除法,并在黑板上写下五六个例子):你能发现哪个分数与哪道除法有关系吗?
生3:我发现1÷3和?有关系,它们是相等的。
师(板书:1÷3=?):怎么解释其中的道理?
生4:我可以用分饼来解释。把1个饼平均分给3个人,每人就得?个饼。
师:对,把1个饼平均分给3个人,可以用除法算式1÷3,结果是多少呢?
(教师边说边移动教具,并强调1个饼的?就是?个饼,如图2)
[设计意图:把课题作为学习素材,在适当的引导下,学生自然地产生疑问,产生探索知识的欲望。回顾旧知识能唤起学生对分数基本含义的记忆,同时,使用教具引导学生认识1个饼的?就是?个饼,这为后续学生的分析和表达打下坚实基础。]
二、逐层探究,自主释问
1.加深感知,初步归纳
师:分数与除法有什么关系呢?不着急,通过一个例子就下结论,太仓促了。我们继续研究。如果把3个饼平均分给4个人,每人分到几个饼?算式怎么列?它的商能用分数表示吗?在纸上画一画、写一写你的想法。
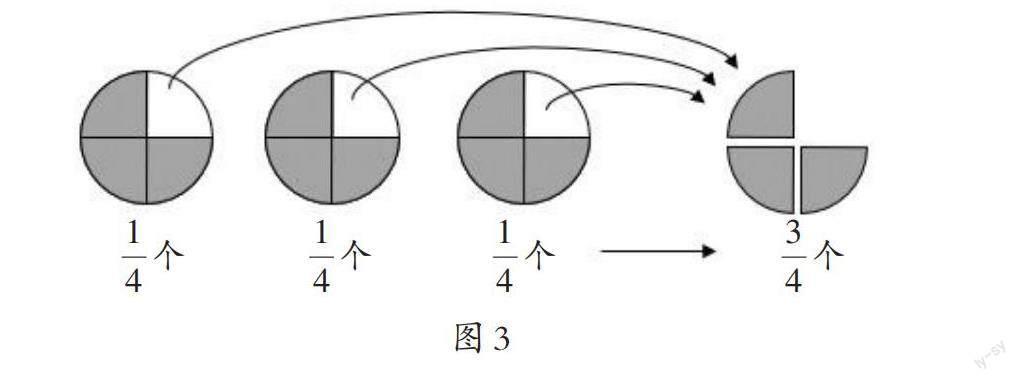
生1:把第一个饼平均分成4份,每人分到?个;把第二个饼平均分成4份,每人也分到?个;把第三个饼平均分成4份,每人也分到?个。一共是3个?个,所以每人分到的是?个饼。
生2:3个饼都平均分成4份,一共就是12份,平均分给4个人,每人分到3份,因为每份是?个饼,所以3份就是?个饼。
师:同学们的研究过程很精彩,虽然方法不同,但得到结果是一致的,也就是3÷4的商是?。我们可以用最基本的思路再来分析一遍。(出示图3)
师:现在有两个例子了。你觉得分数与除法到底有什么关系?
生3:我发现被除数就是分数里的分子,除数就是分数里的分母。
师:你说的意思能用图表示吗?(引导学生在板书的算式中连线,如图4)
师:好像的确如此!再试一个算式“2÷5”。
生4:2÷5等于?,把1个饼平均分成5份,每份是?个饼,2个?就是?。
[设计意图:有了前面分饼的经验,学生能比较顺利地通过画一画、分一分来独立研究3÷4的商。经过教师引导,学生进行了首次归纳,初步发现了分数与除法的关系。]
2.观察思考,提出问题
师:爱动脑筋的同学心里面一定产生了一些疑问吧!请说一说。
(给学生思考时间)
生5:被除数大于除数的除法还是这样吗?
生6:被除数等于除数的时候呢?
生7:整除的时候商也能用分数表示吗?
……
师:学习就是要这样。在看似得到结论的时候,还能有质疑的精神,能勇敢地提问,这不但需要智慧,还是一种了不起的能力。
[设计意图:学生看似已经归纳推理出了分数与除法的关系,但不是很确定,更多的是简单盲从或想当然的心态。因此,教师在此处开启一个提问的“窗口”, 鼓励学生深入思考,从而发现问题并勇敢提出疑问,进而形成批判性思维。]
3.再度探究,深刻感知
师:除法算式5÷4等于几?
生8:等于[5/4]。
师:[5/4]的分子比分母大,你们是怎么理解5÷4=[5/4]的?
生9:把每个饼平均分成4份,每次拿?个饼,5次就是[5/4]个饼。
(因为出现了分子比分母大的新情况,所以教师和学生一起借助教具将整个过程进行梳理,如图5所示)
生10:我的方法跟他的不一样,5个饼平均分给4个人,可以每个人先分到1个,剩下的1个饼再平均分成4份,每人又得到?个,所以每个人就是1个还多?个。
师:虽然生10的分法不同,但结果和生9的是一样的——1个饼里面有[4/4]个饼,再加?个饼,也就是[5/4]个。
(教师将1个饼补画成[4/4]的样子)
师:5÷4的商确实可以用[5/4]表示。看来被除数大于除数的时候,这样的关系依然成立。再算算7÷3等于多少?
……
师:刚才有同学问“被除数等于除数的时候,这个算法是否成立”,谁来举个例子说说看?
生11:5÷5。
师: 5÷5=5/5。5个?正好是1张饼,跟5除以5等于1一样。
4.概括归纳,得到结论
师:我们已经研究了很多例子,有被除数小于除数的,有被除数大于除数的,还有被除数等于除数的,三种不同的情况却有相同的结论。对于分数与除法的关系,你能用一个式子简约地表示吗?
生12:可以写成“被除数÷除数=[被除数/除数]”。
师:也可以用字母表达,写成[a÷b=a/b],当然,这里的[b]不能等于[0]。
[设计意图:根据学生提出的问题,教师组织学生深度探究。学生通过研究被除数小于除数、被除数大于除数、被除数等于除数的除法与分数之间的关系,将前面不完全归纳得出的结果依次进行检验,从而在完全归纳中得出结论,深刻地建构了分数与除法的关系,并切实地感受到了完全归纳思想方法的实用性。]
三、知识运用,加深理解
1.巩固练习,体会价值
师:我们归纳得出了分数与除法的这个关系有什么用呢?一起来看大家之前写的这些除法算式,它们的商分别是多少呢?
生1:20÷4[=20/4],8÷3[=8/3],113÷19[=113/19]。
师:看了这些结果,你有什么感受?
生2:用分数表示除法的结果太简单了!
师:两个整数相除的商可以用分数表示,那么你们之前所列举的分数,它们又分别是哪个除法算式的商呢?(学生回答略)
师:看见分数就能想到除法,厉害!
[设计意图:借助课前学生举的除法和分数的例子进行练习,素材简单,形式灵活,让学生能够很好地感受到所学知识的用途,感受到分数的另一个来源。]
2.问题延伸,学法总结
师:你还有什么疑问吗?
生3:被除数或除数是小数的时候也是这样的关系吗?
生4:分数除法的时候也会这样吗?
……
师:这些问题又能引发我们进一步思考。在学习中会提问太重要了,希望同学们能保持這样的学习习惯。
【课后有感】
用以上思路执教的“分数与除法”不但让人眼前一亮,课堂的效果也令人十分满意。这节课的创新突破之处,主要就是“学生提问、以问引学”促成了学习的真实发生和思维的切实提升。
一、自主开展提问、释问等活动,学习真实发生
整个课程可以看作是由学生的提问、释问(即探究问题和解决问题)等活动串联而成的。学生的提问分为三轮,每一轮的提问都是学生真实思考的表现,所提出的问题都激励了学生主动地探究和解决问题,解决问题后又引发新的问题……学习在这样的提问、释问中真实发生,深入发展。例如,课堂一开始的提问激发了学生的学习兴趣,学生明确了探究方向;探究两个例题后,学生发现其中隐含的关系,此时提出更深入的问题,自主探究其他类型的除法,通过三种类型的除法,正式构建了分数与除法的关系,解决了之前的问题。学生自己提问、自己探究、自己解决问题,学习活动在学生独立思考的基础上展开。这样的课堂让学生兴趣高涨,积极参与,学习活动生动而具有鲜明的特色。
二、充分经历完全归纳等过程,思维切实提升
本课的最大特色是将教材上的不完全归纳改为完全归纳,从而建立了分数与除法的关系。这么做的原因是推理包括合情推理和演绎推理两种,小学生主要接触到的是合情推理中的不完全归纳推理。然而,随着年龄的增长和理性思维的发展,学生在学习的过程中会产生疑问:“其他例子也是这样吗?”或“为什么都是这样的呢?”这些疑问表明学生的思维已经迈向了更高的水平。在这个时候引入演绎推理是适时的,它有助于学生思维水平的提升。
从本课可以看出,学生通过研究两个除法算式来归纳出结论时,伴随的是问题的出现,如“被除数大于除数和被除数等于除数的情况是否也是如此?”这类问题反映了学生思维的严谨性,学生渴望对问题进行分类研究,从而实现完全归纳。在教师的引导下,学生经历了完全归纳的思维过程,从而丰富了对推理的体验(完全归纳推理是演绎推理的一种),逻辑思维和思考能力也得到了有效的锻炼。
此外,学生在课堂中多次发现并提出有意义的数学问题,这也促进了他们批判性思维和创造性思维的发展和锻炼。这与《课程标准》的强调是一致的。
通过对这节课的研究,笔者再次认识到,数学教学应该抓住知识的育人价值,重视学生的学习心理,引导学生提出问题并自主探究,以问题为引导使学生更加主动和深入地学习。这种教学方法有助于学生更深刻地建构知识,更有效地提升思维水平。
(责编 金 铃)
