基于动力学的自适应多段回溯前推实时速度规划算法开发*

谢翰君，王 林，王钦若

（1.广东工业大学 自动化学院，广东 广州 510000；2.国工信（沧州）机器人有限公司，河北 沧州 061000）

0 引言

在数控系统中，速度规划算法是研究的热点之一，因为它对数控系统的速度、精度和运动平稳性具有重要的影响[1-2]。在加工复杂曲线时，为了实现高效加工，通常希望电机按照最大加速度Amax尽可能加速，以达到理想的最大速度。但是，这样的加减速过程可能会引起刚柔耦合、重负载平台的残余振动[3-4]，从而影响零件的加工精度和表面质量。因此，如何平衡加工平稳性和高效性是一个具有挑战性的问题，也是众多学者长期以来关注和研究的热点问题。

文献[5]充分论述了单段（线段）回溯前推算法，避免了由于速度突变所引起的冲击，并在嵌入式平台仿真测试了该算法。文献[6]给出了直线间构造圆弧平滑过渡的轨迹规划算法，为解决因加工路径方向改变而引起冲击的问题提供了较好的解决思路。文献[7]给出了双向扫描速度规划算法，实现连续小线段的速度衔接，但该算法本质上属于离线规划，不太适合实时高速的应用。文献[8]-[10]通过计算相邻小线段拐角处所允许的最大速度，给出微小线段连续前瞻算法。文献[11]给出了考虑弓高误差和向心加速度的自适应速率规划算法。但上述算法都没有考虑实际平台动力学的影响，可能会激起刚柔耦合、重负载平台的残余振动，影响零件的加工精度。文献[12]提出的实时速度前瞻算法基于系统模型动力学，但该模型仅为一阶模型，因此对于难以建立精确模型的刚柔耦合、重负载龙门双驱XY平台系统，该算法可能不太适用。

由此，开发一种同时考虑弓高误差、向心加速度、速度平稳性、实际系统动力学的速度规划算法，很有必要。

1 系统架构

基于PC 的实时控制器架构如图1 所示。该架构采用了工业上广泛应用的EtherCat 总线[13-14]作为实时系统。其主要包括两个程序：CNC 解析器和EtherCat Master。CNC 解析器将加工文件的图形字符串信息转换成直线/圆弧结构体数组，并将其缓存在两片交换内存中。EtherCat Master 主要由两个线程组成：规划线程和S曲线插补线程。规划线程对各段直线/圆弧实现所提速度规划算法。该线程主要包括基于动力学的初步规划算法模块和自适应多段回溯前推速度规划算法模块。基于动力学的初步规划模块先通过直线段的起止坐标，圆弧段的起点、中间点和结束点坐标计算线段长度、圆弧半径、圆心坐标等信息，然后结合弓高误差约束、向心加速度约束、半径约束和系统动力学等信息，该模块得出各线段的实际加速度、动力学约束速度Vrr、向心加速度约束速度Vrmax和弓高误差约束速度Vctf，并将其存放在队列中。自适应多段回溯前推算法模块调用该队列的信息，规划出各线段的初始速度Vs、最高速度以及末速度Ve，并将这些信息传递到S曲线插补线程。插补线程生成的插补点队列通过EtherCat 总线发送到各个EtherCat slave，实现龙门双驱XY平台的运动。

图1 系统架构图

以下先介绍基于动力学的初步规划算法。

2 基于动力学的初步规划算法

任意复杂的曲线都可由直线和圆弧组成，对各段直线/圆弧选用S曲线加减速算法可确保数控系统的加工速度和精度[1]。要使用S曲线加减速算法，需要首先确定每段直线或圆弧的长度L、初始速度Vs、最高速度、末速度Ve和加速度等参数。这个过程称为初步规划。

初步规划的普遍方法如下：

（1）对于直线，由式（1）判断该段直线的线长是否能实现期望速度F。

式中，lr为实现期望速度F的最小线长。若线长L＜lr，需由式（2）重新计算最大可达速度。

式中，Ts为插补周期，δ为弓高误差，r为圆弧半径。于是得：

为了更准确地考虑系统的伺服动力学模型，除了考虑上述的约束条件，文献[12]提出需要进一步考虑该系统的动力学特性，并给出基于系统一阶动力学模型的速度规划算法。然而，文献[15]指出龙门双驱平台是一种强耦合系统，实际上很难建立起其准确的模型。文献[16]采用实验试错的方法，基于系统特征给出了点位离散轨迹算法，以优化系统在固有频率处的最小激励幅值，从而提高微小线段加工性能。基于上述研究，本文提出使用实验方法来确定龙门双驱平台的动力学参数：

（1）选取一段微小线段（如10 mm 的直线），线段从零开始平滑加速并减速到零，则平滑加速所需的最小时间定义为T0；

（2）对于线长L的线段，其不含匀速段时的实际加速度，定义amin≤≤Amax，其中amin为系统的最小加速度，由实验方法确定；

（3）对于r=1 mm 的小圆，平滑运动一周所需的最小时间定义为Tω，则圆的动力学约束速度Vrr=。

因此，对于直线和圆弧，同时考虑弓高误差约束、向心加速度约束及动力学约束的加速度分别为：

将式（1）、式（2）中的Amax改写为，对于直线，得：

对于圆弧，得：

3 基于动力学自适应多段回溯前推算法

在完成基于动力学的初步规划后，本节将介绍基于动力学自适应多段回溯前推算法。

文献[5]对单段回溯前推算法进行了详细阐述。设有当前段i，单段回溯前推算法的核心思想是保证回溯段（i+1）的出口速度为零，即Ve,i+1=0，并确保在两段线段的衔接处不发生速度突变，即Ve,i=Vs,i+1，以保证能够无冲击地完成每段线段的运动。

本节在单段回溯前推算法的基础上，进一步提出基于动力学自适应多段回溯前推速度规划算法(以下简称多段回溯算法），该算法同时考虑了弓高误差约束、向心加速度约束和动力学约束。考虑到龙门双驱XY平台的刚柔耦合特性和加工精度要求，本文设定线段之间的衔接必须满足相切的情况下才使用多段回溯算法。此外，假设直线之后只能与圆弧相切，而圆弧之后则可以与直线或圆弧相切。

假设有连续相切的n段线段，起始段(i)为直线，起始速度Vs,i=0，定义下一段(i+1)圆弧的预计衔接（入口）速度为Vs-,i+1=min(F,Vrmax,i+1,Vctf,i+1,Vrr,i+1)，则i段的预计出口速度Ve-,i=。由此，定义i+1 段出口速度为零的判别式如下：

若式（12）成立，则多段回溯算法结束；若式（12）不成立，则继续回溯下一段（i+2）。需区分i+2 段为直线或圆弧，定义i+2 段出口速度为零的判别式如下：

（1）当i+2 段直线时：

（2）当i+2 段圆弧时：

类似的流程即可自适应回溯i+3,i+4,…段，具体算法流程如图2 所示。

图2 自适应多段回溯前推算法流程图

4 实验

本节将会给出所提算法将与文献[11] 中的自适应速率算法和文献[5]中的单段回溯前推算法的实验对比。

实验将在图1 所示的龙门双驱XY激光切割平台上进行。该平台的XY轴采用了表贴式永磁同步直线电机，单轴连续推力为191 N。伺服驱动器采用了SANYODENKI RS3A05A。反馈装置采用了RENISHAW 增量式光栅尺，其分辨率为1 μm。光源采用SYNRAD Ti100 脉冲CO2激光器,工作波长为9.2 μm，峰值功率为400 W。与龙门双驱XY平台及所提算法相关的参数见表1。

表1 平台及所提算法相关参数

本实验采用了基于PC 的实时控制器，其采用了J1900 2.4 GHz CPU 和2 GB 内存。图1 所示的CNC 解析器在Qt IDE 开发，规划线程和插补线程运行在Ether-Cat 实时主站中。其中，CNC 解析器、规划线程和插补线程的定时器周期分别为20 ms、5 ms、1 ms。为了确保EtherCat 实时主站的两个线程能够同步同一个规划线段，在两个线程间设置了线程互斥锁。插补线程采用了文献[1] 中的 5 段S曲线插补算法。

根据图2 中的算法流程图，可以看出自适应段数的增加会导致算法时空复杂度的增加。考虑到代码实现难度和系统实时性，设定最大自适应回溯段数为2。

4.1 与自适应速率算法的对比

下文先给出与自适应速率算法的对比，测试图形及相应速度曲线如图3 所示。

图3 算法对比

各轴位置偏差如图4 所示。

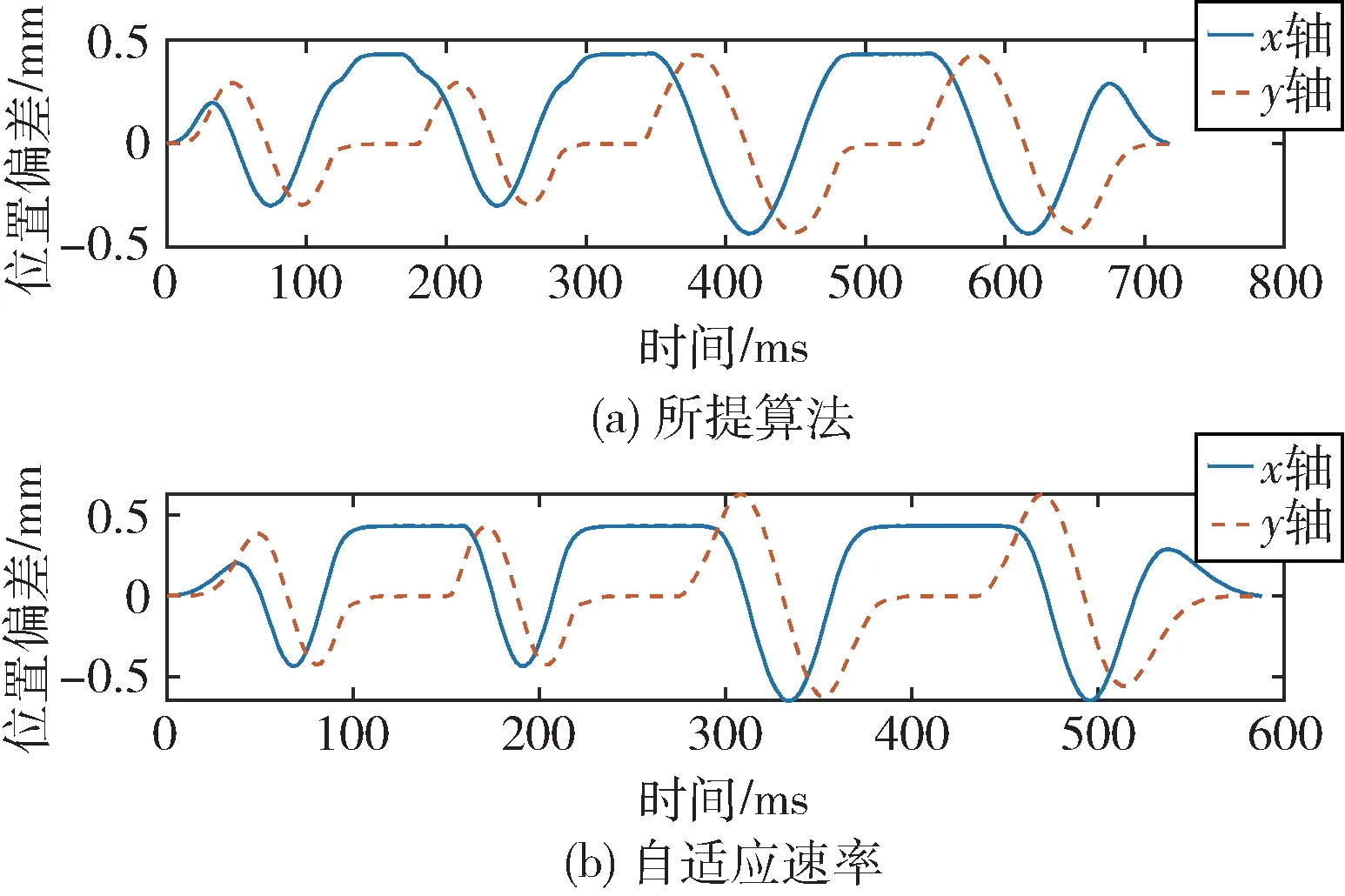
图4 位置偏差曲线对比

R=1 mm 及R=2 mm 圆的目标位置和实际位置曲线如图5、图6 所示。

图5 R=1 mm 圆的实际曲线与目标曲线对比

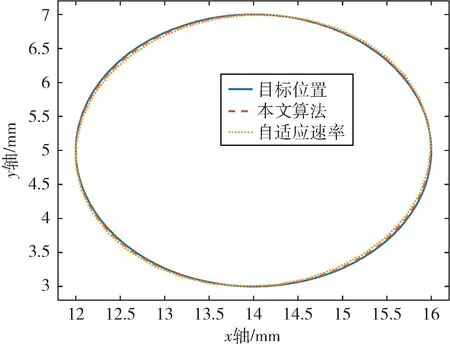
图6 R=2 mm 圆的实际曲线与目标曲线对比

实际曲线采样点与圆心距离如图7 所示。

图7 采样点到圆心距离曲线对比

由图6、图7 中可知，所提算法得到较小的误差，实际圆的加工曲线更接近理想圆。由于自适应速率算法主要考虑最大向心加速度与圆弧半径，忽略了系统的动态特性，导致圆弧的加工速度较高，产生了了较大的轴位置偏差和加工误差。由表2 可知，相比自适应速率算法，对于R=1 mm 圆，最大轮廓误差减少58%；对于R=2 mm 圆，最大轮廓误差减少61%。

表2 圆轮廓误差对比

4.2 与单段回溯前推算法的对比

接着将给出与单段回溯前推算法的对比实验，测试图形如图8 所示，性能对比如图9 所示。

图8 测试图形-椭圆

图9 椭圆曲线性能对比偏差

由图9 可知，所提算法相比单段回溯前推算法，加工时间减少了17%。这是因为单段回溯前推算法必须保证回溯段的出口速度为零。由图8 可知，与起始段圆弧相接的是一段较短的直线，为保证该段直线的出口速度为零，意味着在这两段线段相接处只能规划较低的衔接速度。因而其最终速度曲线呈“高低起伏”形状，与此相比，所提算法的速度曲线更平顺。

最后对字母图形S 进行激光切割测试，激光能量脉宽调节(PWM)设置为10%。测试图形如图10 所示，性能对比如图11 所示，激光切割效果对比如图12 所示。

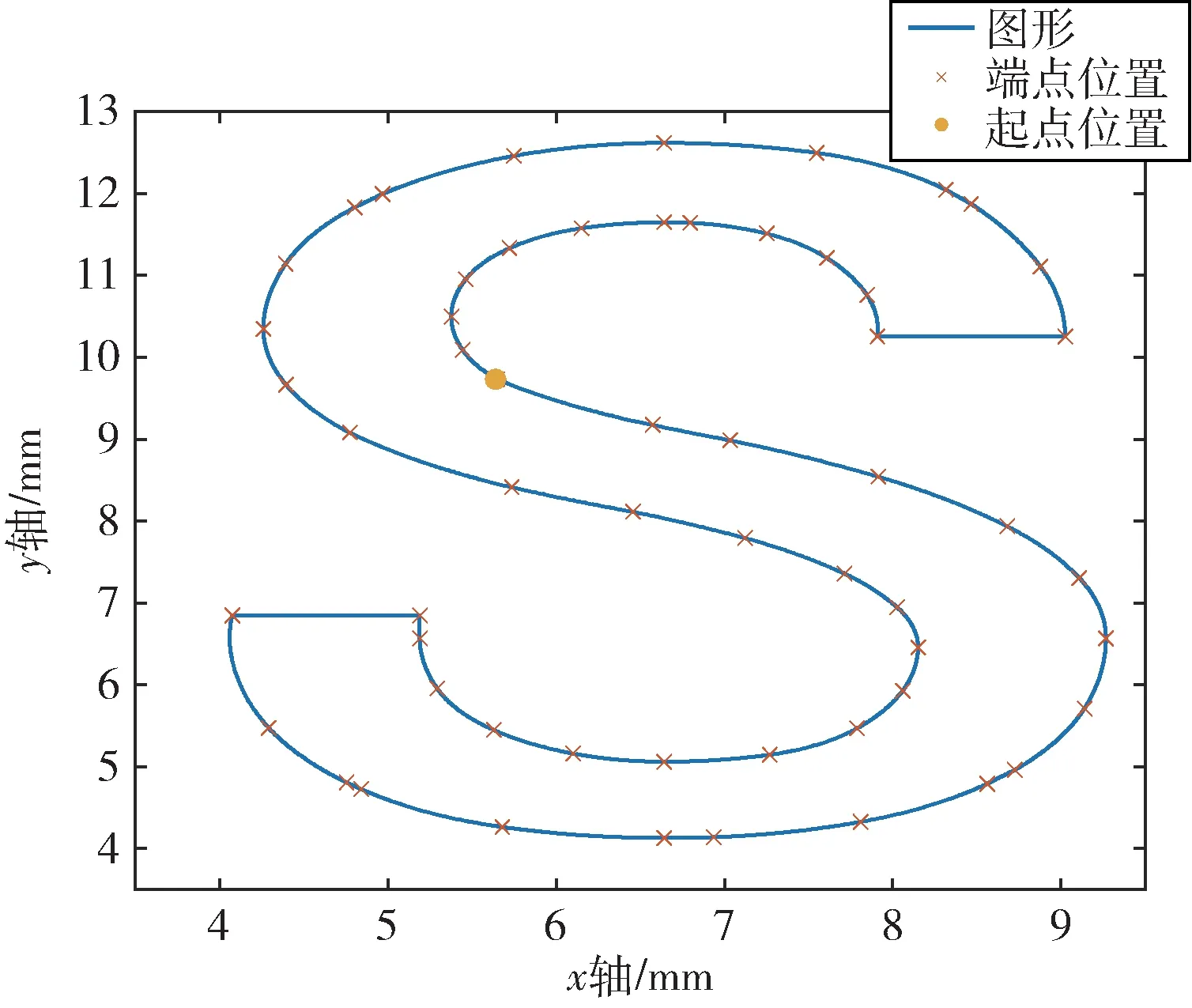
图10 测试图形-字母S

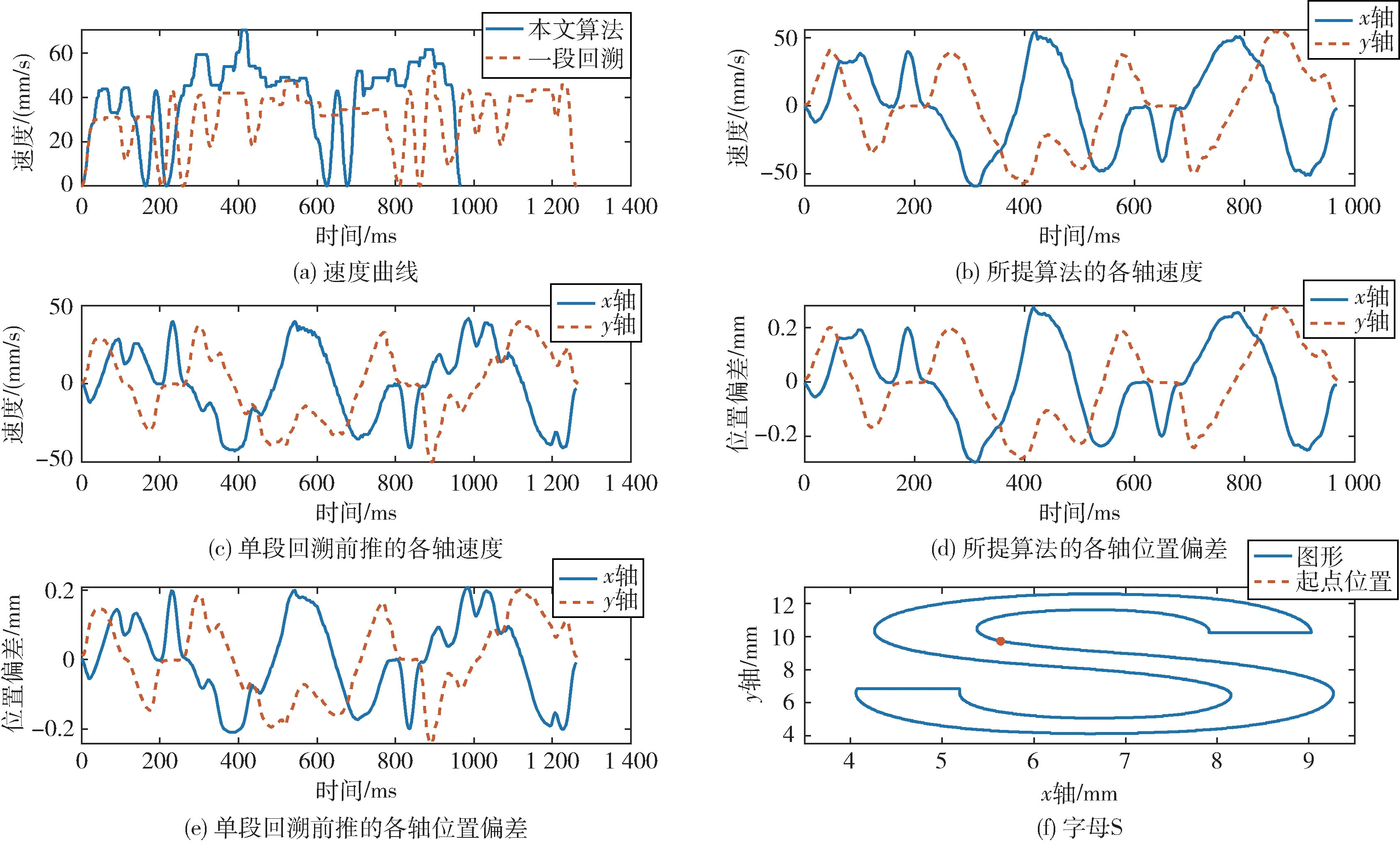
图11 字母S 性能对比

图12 激光切割效果对比

由图11 可知，所提算法相比单段回溯前推算法，加工时间减少了25%。由图12 可知，得益于更平顺的速度规划曲线，相比单段回溯前推算法，由于激光能量过于集中而造成切割轨迹碳化的迹象也大为减少，激光切割质量更高。

5 结论

本文采用基于动力学的自适应多段回溯前推实时速度规划算法，该算法同时考虑了弓高误差约束、向心加速度约束、速度平稳性以及实际系统动力学约束。在龙门双驱XY激光切割平台上，所提算法与自适应速率算法以及单段回溯前推算法进行了对比。与自适应速率算法的比较结果表明，本算法能够获得更好的加工精度。对于R=1 mm 圆，最大轮廓误差减少58%；对于R=2 mm 圆，最大轮廓误差减少61%。与单段回溯前推算法的两个对比测试结果则表明，所提算法的加工效率分别提高17%和25%，并且获得更优的激光切割质量。总体而言，所提算法简单有效，具有较大的应用价值。