基于FREAK特征的多视角影像匹配算法研究*
2023-12-25杨阳,王瑞,宋伟
杨 阳,王 瑞,宋 伟
(1.黄河水利委员会信息中心,河南 郑州 454000;2.赣南科技学院,江西 赣州 341000)
0 引言
影像匹配是图像处理和计算机视觉研究领域的热点问题,是摄影测量自动化的关键技术,其在计算机视觉、3D重构、目标识别、图像拼接领域有着广泛的应用[1-4]。根据匹配算法实现过程中利用图像信息的不同,现有影像匹配算法多以灰度信息和特征信息为基础。其中,基于灰度的影像匹配算法实现简单、匹配精度高,不足之处在于匹配速度慢、结果易受噪声影响。而以特征信息为基础的算法,因稳定性好、效率高而得到了广泛应用。以特征信息为基础的匹配算法的关键是如何实现影像局部不变特征信息的提取,如边缘点、线特征、矩特征等,进而采用相似性度量准则进行特征点匹配。点特征因具有不随光照、投影、平移、缩放的变化而变化的优良性质而被广泛采用。目前,以点信息为基础的特征提取算法主要有Forstner算子、Moravec算子、SUSAN算子和Harris算子等。
基于点特征的影像匹配主要由3个步骤组成:特征点检测、特征描述以及特征匹配。具有代表性的算法主要有SIFT算法、SURF算法、ORB算法[5]以及BRISK(Binary Robust Invariant Scalable Key-Points)算法[6]等。
SIFT(Scale Invariant Feature Transform)算法[7]是由David Lowe提出的,该算法稳定性好,信息量丰富,能够较好地克服由光照和影像几何形变导致的影像缩放和旋转变化,但算法时间复杂度高。针对该算法,不少学者提出了改进算法,如ASIFT[8]、PCA-SIFT[9]以及线特征与SIFT点特征相结合的算法[10]等。
BAY等[11]提出了SURF(Speed Up Robust Feature)算法,其对SIFT算法进行了改进,匹配速度得到了明显提升,但是算法精确度却降低了。
受光照、尺度和旋转等因素的影响,基于特征的影像匹配算法效率较低。针对上述问题,本文采用SIFT与FREAK(Fast Retina Key-Point)[12]特征描述相结合的算法研究了具有不同旋转角度的影像匹配,并将该算法与其他算法进行对比。
1 基于FREAK特征的影像匹配
1.1 特征点提取
特征点信息提取主要包括以下几个步骤:
a.建立尺度空间。目的是检测在尺度变化时仍然稳定的特征。
b.检测极值点。在三维尺度空间中,将采样点与同尺度、相邻尺度的26个点进行比较,若该点是局部极值点,则将其作为候选关键点。
c.获取关键点位置、尺度信息。基于三维二次函数,对采样点进行拟合,得到关键点的精确位置信息与尺度信息。通过该函数拟合可较好地去除边缘点和对比度较低的候选点。
d.确定主方向信息。基于相邻像素梯度方向,获取梯度直方图。峰值所在的方向表示关键点所在主方向信息。
1.2 基于FREAK算子的特征点描述
1.2.1 特征点信息描述
FREAK描述符采用与视网膜感受域相似的分布结构,其中心点即为特征点位置。对应的采样点在同心圆上均匀分布。以σ作为特征点尺度信息,则可得到同心圆半径:M1σ,M2σ,…,Mkσ,其中k代表采样点层级数。图1为视网膜结构示意图和FREAK算子采样点结构图。
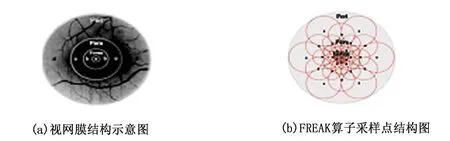
图1 采样点结构图与视网膜结构示意图比较
图1(b)所示黑色点位即为采样点,首先通过高斯平滑处理来消除采样点噪声,高斯核大小取决于采样点所在同心圆的半径。同时,采用重叠结构构建采样点的感受域,通过感受域的重叠来获取更多信息。
以采样点对强度信息为基础进行比较,同时将比较结果进行级联形成对应的FREAK特征描述符,其属于二进制描述符。以M作为特征点描述符,则有
(1)
(2)

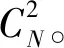
a.首先构建一个矩阵A,矩阵的每一行构成对应的FREAK描述子。
b.计算矩阵A每一列的方差值,矩阵每一列信息的多少与方差值成正比。筛选出方差值最大的列,计算其与其他列的协方差,并将协方差最小的添加到新的描述向量。
c.当达到设定的维数上限Nmax时结束运算,反之则返回步骤b。
基于以上的筛选、排序处理,描述符外层的采样区构成其低维度信息,位于中心的采样区构成其高维度信息。由此可知,外层采样区域表达了对象的基本特征信息,中心的采样区域则与细节信息有关。
1.2.2 方向分配
FREAK算法获取特征点方向的计算过程与BRISK算法相近。在BRISK算法的长距离采样点对基础上,FREAK算法筛选得到45个对称点对,计算梯度信息。图2为对比点对集合。
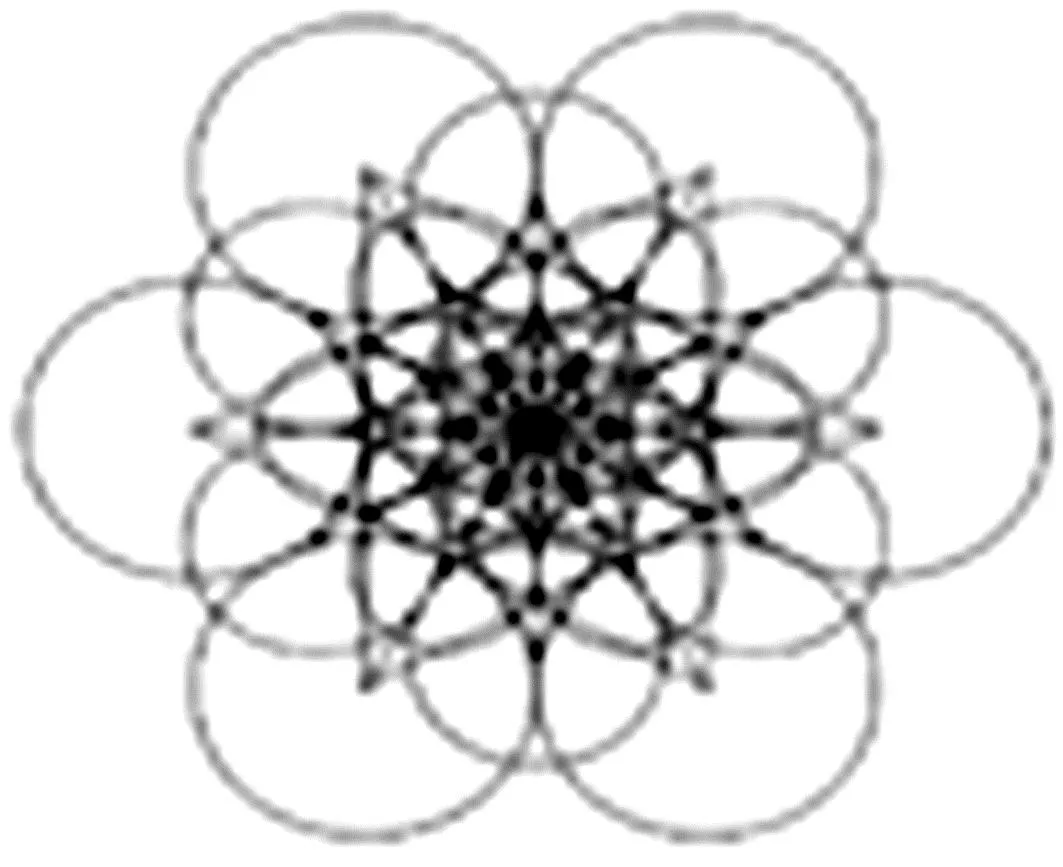
图2 特征点方向的对比点对集合
特征点对集合计算公式为
(3)

FREAK描述符的采样结构为圆形对称,因而具有旋转不变性。同时通过高斯平滑处理,较好地降低了噪声干扰。故而,针对旋转、尺度变换和噪声等,FREAK特征具有稳定的局部不变性。因此,基于FREAK特征描述的算法可以实现影像的快速配准[13]。
1.3 特征点匹配
对于不同旋转角度影像的匹配,本文采用比值提纯法(NNDR)进行粗配准,然后采用RANSAC算法[14]进行精确配准,具体步骤如下:
a.采用K近邻算法(KNN)搜索特征点,然后根据特征点之间的距离阈值判断特征点是否符合要求。若小于设定的阈值,则是对应的匹配点。
b.由步骤a中K的取值为2,可检测到与样本点对应的两个特征点,分别为最近邻和次近邻点。然后根据最近邻和次近邻特征点之间的距离比值关系来进行粗配准。
c.利用RANSAC算法对步骤b中的粗配准结果进行筛选,得到精确配准结果。
2 实验与分析
基于两组无人机影像数据,利用本文算法对其进行配准实验,并分别统计匹配到的特征点数及算法耗时。为了验证本文算法的有效性与准确性,将结果与SURF算法、SURF-FREAK算法的实验结果进行对比。
对于影像的匹配效果,采用正确率和两幅图像所有匹配特征点对之间坐标的均方根误差ERMS作为评价标准,其中匹配正确率的定义为
(4)
式中,Mmatched为匹配到的点对数,Mrightmatch为正确匹配到的点对数。
ERMS的计算式为
(5)

图3、图4分别为将待配准影像旋转30°、60°、90°、145°时的匹配效果图。

图3 Image 1不同旋转角度的配准结果

图4 Image 2不同旋转角度的配准结果
算法的运行结果分别见表1、表2。

表1 Image 1不同角度下SIFT-FREAK算法与SURF、SURF-FREAK算法的结果
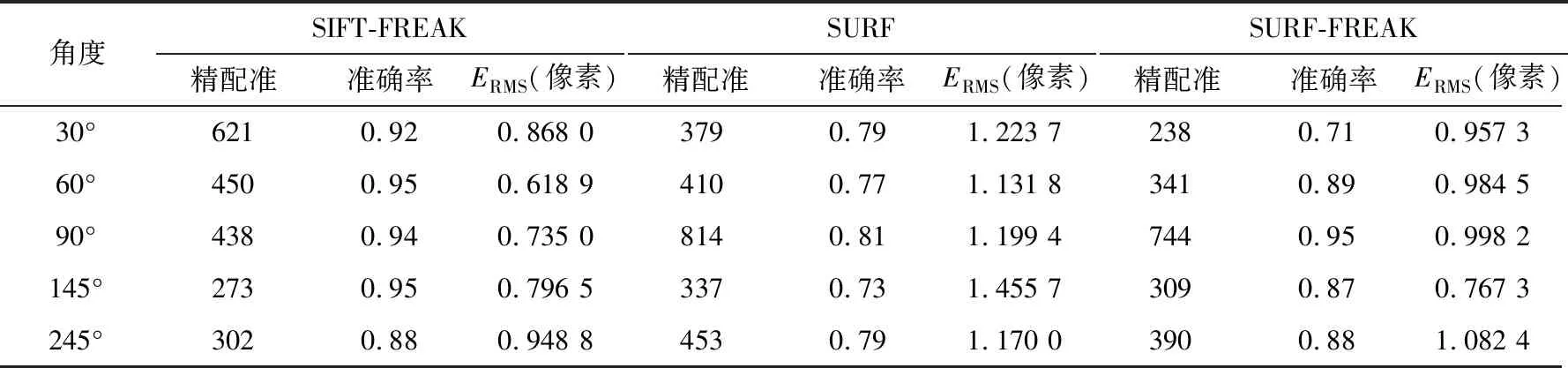
表2 Image 2不同角度下SIFT-FREAK算法与SURF、SURF-FREAK算法的结果
根据图4、图5以及表1、表2可知,对于不同角度的影像匹配,SIFT-FREAK算法匹配效果较好,其结果准确率高,且影像间旋转角度差异大时该算法的准确率能保持在90%以上,匹配得到的同名点精度高,能够达到亚像素级的匹配精度。另外,在利用上面2组影像数据进行配准实验的同时还统计了该算法的时间效率(见表3)。

表3 各算法不同角度的时间效率
综上可知,该算法具有以下优点:
a.具有较高的准确率;
b.匹配到的特征点具有较高的精度;
c.对不同旋转角的匹配结果具有较好的稳定性。
3 结论
针对不同旋转角度影响影像匹配效果的问题,提出了基于FREAK特征的多视角影像匹配算法,得到以下主要结论:
a.该算法有效解决了不同旋转角度影像配准的问题,对于多视角的影像匹配具有较好的效果。
b.采用分阶段匹配的方法,有效提高了匹配结果的准确率和精度。
c.通过采用FREAK描述符,较好地提升了匹配算法的时间效率,可以更好地应用于实践。
