基于PCA-RF的边坡稳定性预测*
2023-12-25林逸晖李广涛杨天雨乔登攀赵怀军
林逸晖,李广涛,杨天雨,乔登攀,王 俊,张 希,赵怀军
(1.昆明理工大学 国土资源工程学院,云南 昆明 650093;2.凉山矿业股份有限公司,四川 凉山 615141)
0 引言
近年来,随着现代工业对矿产资源的需求量日益增加,我国露天矿山的开采规模不断扩大,开采深度越来越大,高陡边坡数量越来越多,边坡灾害发生频次逐年上升。边坡灾害会对人民生命财产安全造成严重威胁,并使生态环境遭受巨大破坏[1-2]。因此,为减少边坡灾害的发生,开展边坡稳定性预测研究具有重要的现实意义。
露天矿山边坡稳定性分析方法主要有定性分析法、定量分析法和数值分析法等[3]。随着计算机技术的发展,机器学习算法被引入边坡稳定性预测研究中。目前用于边坡稳定性预测的机器学习算法有粗糙集理论、模糊逻辑理论、支持向量机、蚁群算法、贝叶斯算法、信息量法、多元逻辑回归、决策树法等[4]。瞿婧晶等[5]采用粗糙集属性约简和相互关系矩阵法进行综合分析,建立了边坡稳定性评价体系,并将其应用于镇江地区下蜀土边坡的稳定性预测中。张云雁[6]采用网格搜索算法对支持向量机模型进行参数优化,并根据边坡特征参数,采用优化后的支持向量机模型对边坡稳定性进行了预测。赵允坤等[7]利用改进粒子群算法(IPSO)对极限学习机的输入权值和隐层偏置进行了优化,建立了基于IPSO-ELM的边坡稳定性预测模型,实现了对边坡稳定性的有效预测。
但机器学习算法也存在一定缺陷,如:粗糙集理论需结合其他算法使用,否则难以有效反映不确定性问题;支持向量机模型对于缺失数据以及参数和核函数的选择较敏感,且核函数及其参数是根据经验选取的,带有一定的主观性;极限学习机存在易过拟合以及可控性差等缺点。
随机森林(Random Forest,RF)是由美国科学家Leo Breiman[8]于2001年提出的,这是一种将Bagging集成学习理论与随机子空间方法相结合的机器学习算法。随机森林以决策树为基本分类器,相对于决策树法,随机森林克服了其易出现过拟合的缺点,降低了异常值可能带来的影响,但计算量较大[9-10]。此外,随机森林对高维数据分类问题有着良好的可扩展性和并行性,并且作为一种由数据驱动的非参数分类方法,使用随机森林算法时无需调参以及分类先验知识[11]。针对随机森林算法计算性能开销较大的缺点,本文利用主成分分析法(Principal Component Analysis,PCA)进行数据处理,过滤冗杂数据,降低随机森林算法的计算量,构建基于PCA-RF的边坡稳定性预测模型,并将其应用于露天边坡的稳定性预测。
1 理论基础
1.1 主成分分析
主成分分析是利用降维思想,在信息损失较少的前提下,将原来具有一定相关性的指标重新组合成一组新的信息互不重叠的综合指标,来反映大部分原指标中所携带的信息量的多元统计方法[12]。主成分分析计算步骤叙述如下。
(1)建立m×n矩阵,m为样本数量,n为每个样本的指标个数。
(1)
(2)将原始数据进行标准化,生成标准化矩阵。
(2)
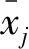
(3)进行KMO(Kaiser-Meyer-Olkin)和巴特利特球形检验。若KMO值大于0.5,表明变量间的相关程度差异较小,数据很适合作因子分析[13];若巴特利特球形检验的结果小于0.05,球形假设被拒绝,表明原始变量之间存在相关性,数据适合作因子分析[14]。
(4)根据标准化矩阵建立协方差矩阵。
(3)
式中,i=1,2,…,n,j=1,2,…,n。
协方差矩阵由标准化矩阵的两两列变量的协方差组成,因此cov(zi,zj)为列变量zi与zj的相关系数,即协方差矩阵为相关系数矩阵。
(5)计算协方差矩阵R的非负特征根λi(i=1,2,…,p)。
|λE-R|=0。
(4)
(6)由计算得到的p个非负特征根计算前q个主成分的累计贡献率。
(5)
(7)根据主成分的累计贡献率选取主成分个数,并生成新变量指标。前q个主成分的累计贡献率达到85%时,即可认为这些主成分中包含了绝大部分原指标所携带的信息量[15]。将生成的新变量指标表示原变量指标:
(6)
式中,x1,x2,…,xn为原变量指标,y1,y2,…,yp为新变量指标,cij与yi互不相关且cij满足ci12+ci22+…+cin2=1。由此完成了数据降维,在信息损失较少的前提下减少了变量数。
1.2 随机森林模型
随机森林{h(X,θk),k=1,2,…,K}是以K个决策树模型作为基本分类器,通过集成学习形成的组合分类器[16]。随机森林算法以待分类样本作为输入,基于决策树模型,采用自上而下的递归方式,从树的根节点开始,在其内部节点上进行属性值的测试比较,然后按照给定的属性值确定对应分支,在决策树的叶子节点得到结果,最后根据每个决策树模型的分类结果投票决定最终输出的分类结果。
随机森林中的{θk,k=1,2,…,K}为随机变量序列,其体现在两个方面:
(1)数据的随机选取。在Bagging集成算法的基础上,利用Bootstrap方法从原始样本集中采取有放回抽样,随机创建K个与原样本集数据量相同的子数据集{Tk,k=1,2,…,K},其中不同子数据集的元素可以重复,同一个子数据集中的元素也可以重复。
(2)待选属性的随机选取。采用随机子空间方法,在随机森林中的子决策树的各节点进行分裂时,从所有的待选属性中等概率随机选取一定的属性[通常选取(log2M+1)个属性,M为属性总个数[17]],再从所选属性中选取最优属性进行节点分裂。
随机森林的分类过程为:
(1)利用Bootstrap方法随机选取数据,生成子数据集Tk,将Tk作为训练集构建K棵决策树。
(2)每棵决策树生长过程中在所有的待选属性中等概率随机选取一定的属性,并从中选取最优属性对每棵决策树的各个节点进行分裂,并且让每棵决策树均不进行剪枝地完整生长。
(3)由完整生长的K棵决策树构成随机森林。
(4)输入测试集样本进行预测,由每棵决策树的输出结果投票决定随机森林输出的分类结果(即每棵决策树输出结果的众数)。
2 PCA-RF预测模型构建及验证
2.1 样本数据
影响边坡稳定性的因素主要有边坡角度、边坡高度、岩土体物理力学性质、岩石强度、岩石结构、孔隙水压、水文条件及地震等[18]。但岩石强度、岩石结构等因素对于边坡稳定性的影响较小,地震等自然灾害出现的概率较低,样本较少。因此,为减少随机森林算法的计算量,提高计算速度,选取岩石容重γ、黏聚力c、内摩擦角φ、边坡角度α、边坡高度H和孔隙水压μ等6个主要影响因素进行边坡稳定性预测[19]。本文基于此6项指标构建随机森林边坡稳定性预测模型,将使用主成分分析降维后的指标作为实际输入、边坡稳定状态“稳定”和“失稳”作为输出进行边坡稳定性预测。
本文选取文献[20-21]中的54组不同且具有明确稳定状态的边坡实例作为研究对象,构建PCA-RF边坡稳定性预测模型。边坡实例数据见表 1,其中:边坡状态“1”表示边坡稳定,“2”表示边坡失稳;稳定边坡为34组,失稳边坡为20组,第55-第58组数据为拉拉铜矿东部露天采场终了边坡数据,以此作为预测实例。

表1 边坡实例数据
2.2 主成分分析
对表 1中的58组数据进行标准化处理,计算得到KMO值为0.665,大于0.5;巴特利特球形检验值为0.000,小于0.05,表明样本数据适合进行主成分分析。对表 1中的数据进行主成分分析,得到各影响因素间的相关矩阵热图(见图 1)。将相关性系数取绝对值后,如在0~0.1,表示无相关;如在0.1~0.3,表示弱相关;如在0.3~0.5,表示中等相关;如在0.5~1.0,表示强相关[22]。

图 1 相关矩阵热图
由图 1可知,某些影响因素间存在较强的相关性,如岩石容重与边坡角度、边坡高度间的相关性系数分别为0.535、0.679,均大于0.5,表明具有强相关性。主成分分析能够将这些指标重新组合成一组新的信息互不重叠的综合指标,从而避免相关性过强可能带来的多重共线性问题。
为确保选取的指标中携带原样本数据的绝大部分信息量,需计算各因素对边坡稳定性影响的贡献率及累计贡献率,结果见表2。

表2 各影响因素贡献率

表3 主成分系数矩阵
由表 2可知,前4项主成分的累计贡献率达到了91.283%,大于85%,表明前4项主成分已携带原样本数据的绝大部分信息量,因此选取前4项主成分生成新变量指标。各主成分系数矩阵见表 3。
将各主成分系数分别除以相应的主成分特征根的平方根,得到因子载荷矩阵(见表4)。
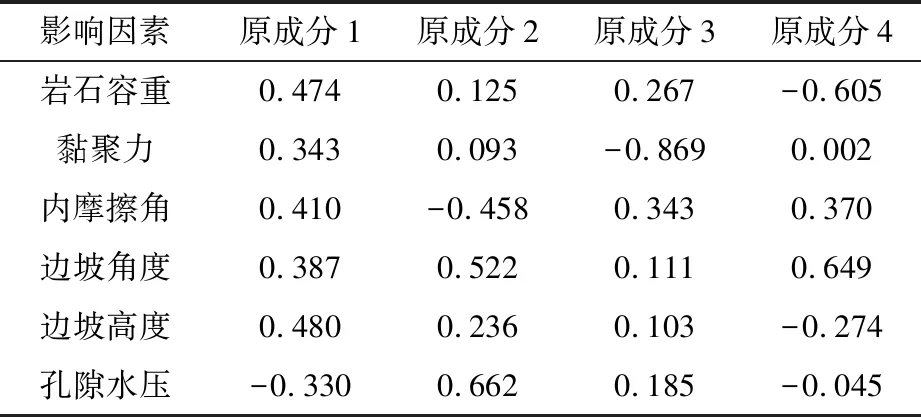
表4 因子载荷矩阵
由因子载荷矩阵可得出新变量指标的表达式:
(7)
经主成分分析后,在降低变量维数的同时,还保证了原样本数据携带的信息量尽可能少丢失。经主成分分析降维后的边坡数据见表5。

表5 经主成分分析降维后的边坡数据
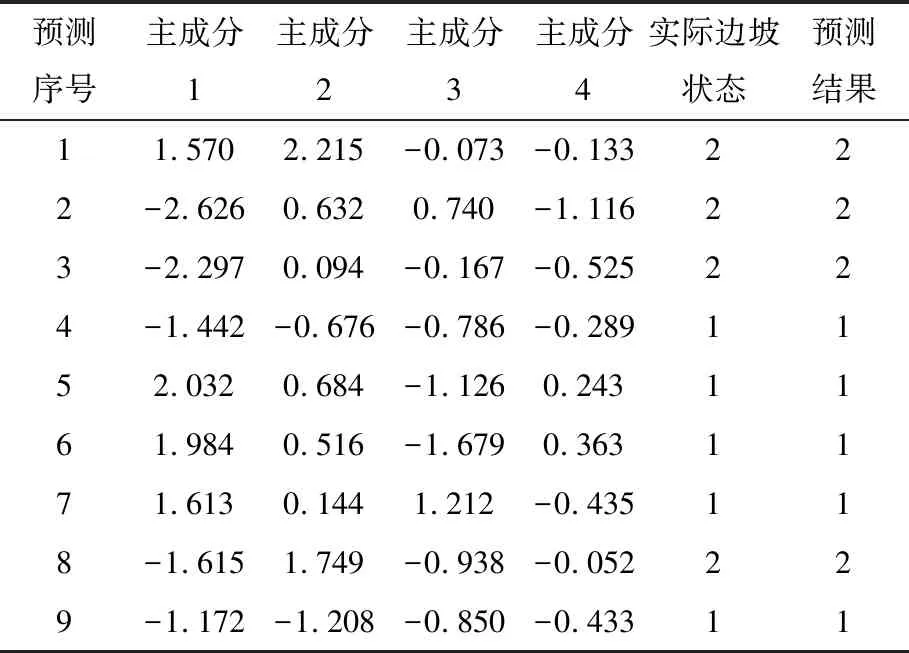
表6 PCA-RF模型预测结果
2.3 建立边坡稳定性预测模型
从降维后的前54组边坡数据中随机选取45组数据作为输入训练样本建立PCA-RF边坡稳定性预测模型,将剩下的9组数据作为测试样本,用来检验该预测模型的准确率。
在使用随机森林进行预测之前,需先设置2个重要参数:随机森林中包含的决策树个数ntree和每棵树节点预选的变量指标个数mtry。若预设的ntree值太小会导致随机森林模型训练不够充分,太大则会导致模型运行速度缓慢;若预设的mtry值太小可能会导致分类器过拟合,使预测精度降低,太大则会增加模型的运算量。综合考虑,本文将ntree值设为500,mtry值设为4。PCA-RF模型预测结果见表 6。
由表 6可知,PCA-RF模型的预测准确率达到了100%。但因随机森林生成训练集时采用Bootstrap有放回自助采样法,输入训练样本中有(1-1/N)N的样本不会被抽取(N为输入训练样本中的样本个数),当N足够大时,(1-1/N)N将收敛于1/e,约为0.368,即有约36.8%的样本数据不会被抽取[23]。因此,该预测模型有可能存在误差,为此需要对该模型进行性能评估。
2.4 交叉验证
模型性能的评估方法有留一法和交叉验证法等,本文选用6折交叉验证法对PCA-RF模型进行性能评估。6折交叉验证法验证步骤为:
(1)将54组样本数据随机分为数据量相同的6组数据子集D1-D6。
(2)取其中的第i组数据子集Di作为测试样本,将其余5组数据子集作为输入训练样本,构建6个随机森林预测模型。
(3)汇总预测结果,开展PCA-RF模型的性能评估。
交叉验证过程中预测模型的参数设置与前文相同,验证结果见表7。由表7可知,模型的预测精度较高,达到了94.44%,表明该预测模型可以用于边坡稳定性预测。

表 7 交叉验证结果
3 工程应用
3.1 预测对象选取
拉拉铜矿矿体主要部分埋藏不深,矿山原设计采用露天开采,露天开采区域分为东部露天采场和西部露天采场,东部露天采场尚未开采至终了境界,其终了边坡稳定状态未知,因此本文选取东部露天采场终了边坡作为预测对象,现场照片见图2。该矿东部露天采场终了边坡东帮设计高度为252 m,坡角为45.57°;西帮设计高度为216 m,坡角为41.75°;南帮设计高度为296 m,坡角为45.89°;北帮设计高度为312 m,坡角为30.05°。露天采场区域岩性主要为片岩,岩石力学参数见表 1中第55-第58组数据。东部露天采场边坡现场照片见图3。

图2 拉拉铜矿东部露天采场

图3 拉拉铜矿东部露天采场边坡
3.2 预测结果分析
将经主成分分析降维后的拉拉铜矿东部露天采场终了边坡数据作为预测数据,输入已训练好的随机森林预测模型中,输出的预测结果见表8。由表8可知,拉拉铜矿东部露天采场终了边坡的东帮、西帮、南帮、北帮均处于稳定状态。
表8 拉拉铜矿东部露天采场终了边坡稳定性预测结果
4 结论
a.本文采用主成分分析对原始边坡数据进行降维,减少了随机森林算法的计算量,建立了PCA-RF边坡稳定性预测模型。
b.边坡实例预测结果表明,PCA-RF模型预测准确率达到100%,并且该模型经6折交叉验证法评估的预测精度高达94.44%,表明该模型可以用于边坡稳定性预测。
c.将PCA-RF模型应用于拉拉铜矿东部露天采场边坡稳定性预测,结果表明,该矿东部露天采场东帮、西帮、南帮、北帮终了边坡均处于稳定状态,该预测结果可为矿山生产和管理提供参考。
