基于博弈论综合赋权-物元可拓理论的岩爆倾向性预测*

2023-12-25郑龙菲周宗红

化工矿物与加工 2023年12期

郑龙菲,周宗红,刘剑

(昆明理工大学国土资源工程学院,云南昆明 650093)

0 引言

岩爆是深部地下工程常见的地质灾害之一。目前,随着矿业[1]、交通[2]、水利[3]等工程逐渐向深部延伸[4],岩爆发生概率随之升高。高烈度岩爆往往会带来巨大的安全风险和经济损失,因此如何准确地预测以及防治岩爆已成为地下工程建设中必须要考虑的问题。

岩爆预测是防治岩爆灾害的有效手段。国内外学者针对岩爆的发生机制,结合非线性理论对岩爆等级预测进行了大量研究[5-6]。吴顺川等[7]运用主成分分析和概率神经网络原理,结合国内外典型岩爆案例,建立了岩爆等级预测模型;过江等[8]利用改进的CRITIC法计算指标权重,结合国内外20组岩爆案例,建立了CRITIC法多维云模型;周科平等[9]利用熵权法计算指标权重,并采用云理论对岩爆等级进行了评价;黄明健等[10]将粗糙集理论与改进后的云模型相结合,为岩爆等级预测提供了一种可靠的方法;卢富然等[11]基于层次分析法(AHP)和熵权法(EWM)计算主客观权重,通过乘法组合计算权重,结合TOPSIS法对岩爆进行了等级预测;梁燕华等[12]将粗糙集理论与层次分析法相结合,通过经验分析确定线性加权系数,对岩爆评价指标进行了赋权,并利用由声发射手段获得的数据对岩爆等级进行了评价。

虽然众多学者基于不同赋权方法对岩爆等级预测开展了大量富有成效的研究,但仍存在一些不足:①由于对岩爆机制的认识缺乏完备的系统理论,主观权重计算受专家经验和水平所限,得出的结论主观性和随机性强,从而影响预测结果的准确性;②权重的组合计算方法大多使用主观性较强的线性加权或简单乘法组合,使得组合权重的计算欠科学,而合理地赋权是保证岩爆等级预测结果准确性的前提。

本文使用粗糙集理论代替主观赋权法,基于粗糙集理论的信息观与代数观,不需要先验知识,同时从数学规律与信息熵等多角度利用数据,避免了主观赋权法的缺点;考虑到多指标之间的相关性,引入CRITIC赋权法,通过博弈论进行综合赋权;引入物元可拓理论进行岩爆倾向性等级判定,并与其他赋权方法预测结果进行对比,验证本文提出模型的可靠性与合理性。将该模型应用于锦屏二级水电站引水隧洞的岩爆预测中,进一步验证模型的可靠性。

1 权重计算与综合赋权基本原理

1.1 粗糙集理论

粗糙集理论(RS)是波兰学者Pawlak于1982年提出的处理不精确、不确定和不完全数据的有效数学工具,其采用目标集合的上近似和下近似来表达模糊化的信息。利用需要处理的数据确定区间的上限和下限。粗糙数的确定不需要预先具有相关经验知识,保持了信息评估的客观性,与其他处理不确定性问题的理论方法具有很强的互补性[13]。

1.1.1 基于代数观的属性权重

粗糙集理论中S={U,V,A,F}是一个决策信息系统;在S中,U={x1,x2,…,xn}为论域,xi(i≤n)是论域中的一个对象。A=C∪D,A为条件属性集,D为决策属性集。

对于给定的知识库M={U,R},任意X⊆U,POSR(X)称作X的正域,其被定义为POSR(X)=U{Y∈U/R:Y⊆X},

(1)根据系统建立的评价指标体系构建决策信息表。

(2)条件属性对于决策属性的重要性为

IC(D)=|POSC(D)|/|U| ,

(1)

式中:POSC(D)为D的C正域,|U|表示案例个数。

任意属性子集Ci关于D的属性重要性为

γ(Ci)=IC(D)-IC-Ci(D) 。

(2)

(3)Ci对应的权重ωi为

(3)

1.1.2 基于信息观的属性权重

决策信息系统S={U,C∪D,V,F},U按照C、D的分类数划分的数据集为X、Y。X={X1,X2,…,Xn},Y={Y1,Y2,…,Yn},条件属性集C与决策属性集D在X、Y上的概率分布为

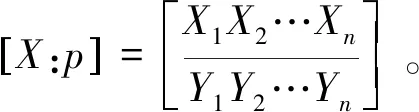
(4)

(1)属性集C的信息熵H(C)与C相对于D的条件信息熵H(D|C)为

(5)

(6)

(2)对于条件属性集C={c1,c2,…,cn}与决策属性集D={d},C-Ci的属性重要性为

I(Ci,D)=H(D)-H(D丨Ci) 。

(7)

(3)对各个属性作归一化处理,得到基于粗糙集理论信息观的权重:

(8)

(4)将基于代数观的属性权重与基于信息观的属性权重使用式(12)经乘法组合得出最终基于粗糙集的属性权重。

1.2 CIRTIC法

CRITIC法是一种比熵权法、变异系数法更为合理的客观赋权法[14],其通过衡量多个指标之间的冲突性与变异性进行赋权,变异性大小代表了同一指标内取值差距大小,由标准差表示,其值越大体现的信息量越多,权重越大[15];冲突性由相关性体现,二者之间成反比。其运算流程叙述如下。

(1)构建初始指标数据矩阵:

X=(xij)m×n,

(9)

式中,xij为第i个对象对应的第j个指标的原始数据。

(2)对原始数据作标准化处理。

(3)计算评价指标相关系数:

(10)

(4)计算权重:

(11)

(12)

式中,σj表示数据的标准差。

1.3 乘法组合法

将由粗糙集理论(RS)获得的权重记为H=(η1,η2,…,ηn),将由CRITIC法获得的权重记为L=(ζ1,ζ2,…,ζn),运用式(13)计算得到组合后的权重:

(13)

1.4 博弈论综合赋权

目前大部分组合权重多基于乘法组合赋权或通过经验选择偏好系数的线性加权进行赋权,其中偏好性系数是由决策者选取的,主观随意性较大,不能科学地反映不同赋权方法的特点。为了解决此问题,在组合赋权的过程中引入博弈论,将不同方法确定的指标权重作一致化、协调化处理[16],找到指标间的最大利益点,进而得到最优组合权重。具体步骤叙述如下。

为了更加科学合理地对不同指标进行赋权,可以采用N种赋权方法得到权重向量ωi,i=1,2,…,N;由此构成初始权重向量集μn={ω1,ω2,…,ωN},i=1,2,…,n;则初始向量权重集的任意线性组合记为

(14)

运用Matlab计算得到相应的系数(α1,α2,…,αN),通过归一化处理得到:

(15)

评价指标综合权重为

(16)

2 可拓学理论与模型构建

2.1 模型构建流程

基于博弈论的综合赋权-物元可拓岩爆预测模型构建流程见图1。

图1 博弈论综合赋权-物元可拓岩爆预测模型构建流程

2.2 岩爆危险性评价指标体系选取

岩爆发生机理复杂,影响因素众多,岩爆预测指标的选取是岩爆等级预测中的重要一步。根据相关研究[8],选取应力系数σθ/σc(S)、岩石脆性系数σc/σt(B)、弹性变形能指数Wet和岩体完整性系数Kv作为岩爆预测指标。将岩爆等级分为无岩爆(Ⅰ级)、弱岩爆(Ⅱ级)、中等岩爆(Ⅲ级)以及强岩爆(Ⅳ级)。以国内外20组工程实例作为样本数据,建立岩爆危险性等级评价模型。

2.3 确定岩爆物元的经典域

物元可拓理论是我国学者蔡文于20世纪80年代提出的,在处理不相容问题方面具有较大优势[16]。依据岩爆等级分级标准,将岩爆危险性等级划分为z个等级,则经典域可以表示为

(17)

式中,N0j为评价对象分级标准的第j等级,cn为第n个评价指标,v0jn为岩爆等级j下第n个评价指标的取值范围,

根据表2,对4个评价指标对应的4个岩爆等级进行无量纲化处理,得到经典域:

2.4 确定岩爆物元的节域

取各个指标全体级别对应的全部范围构成岩爆危险性评价的节域物元:

(18)

式中:Np为全部岩爆围岩等级,vpk为属性ck的取值范围,apk和bpk分别对应ck的上下限。

依据岩爆危险性等级评价的整体取值范围得到岩爆物元的节域:

2.5 计算待评物元

确定待评物元,待评对象有m个,则第i个待评物元为

对表1中数据作标准化处理,确定待评物元,结果见表3。

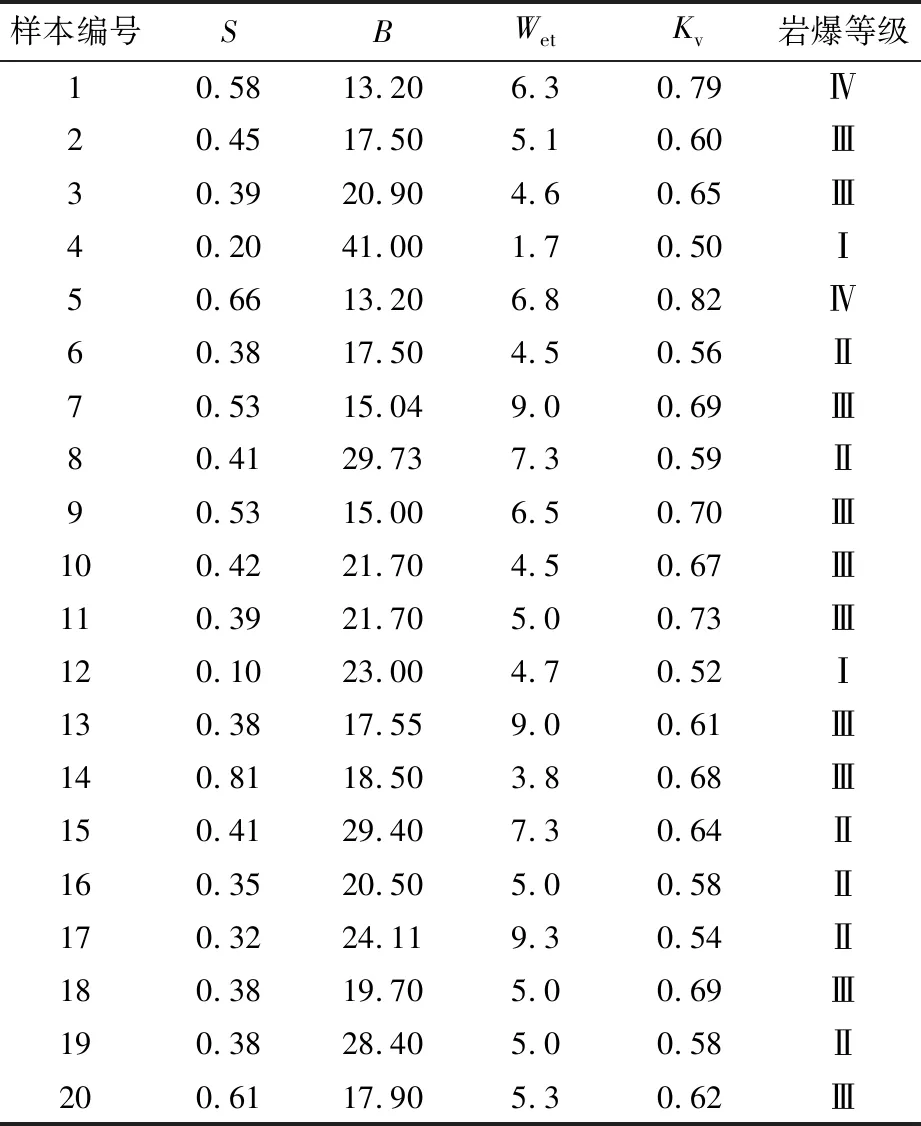
表1 国内外20组工程岩爆数据[8,17-18]

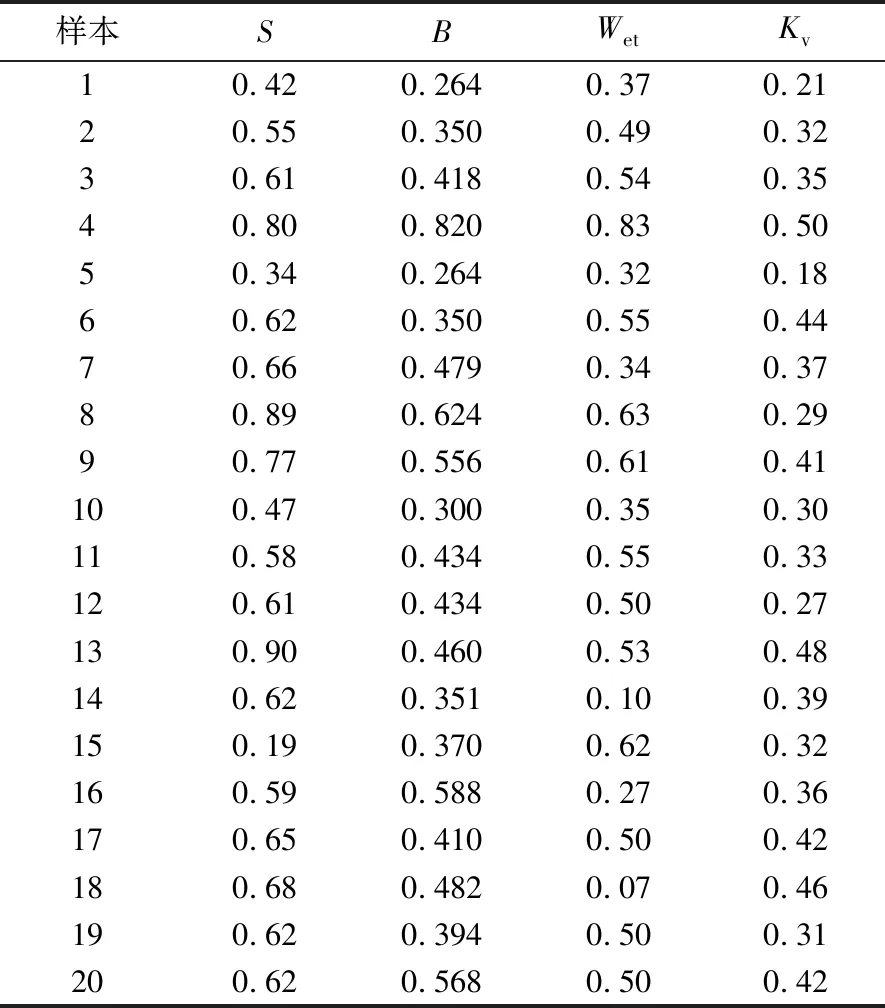
表3 待评物元计算结果

2.6 计算待评价指标与岩爆危险性等级关联度

设第i个待评物元的第k个指标关于岩爆危险性等级j的关联性函数为

(19)

(20)

以样本1为例,利用式(19)、式(20)计算待评价指标与岩爆等级关联度,结果见表4。

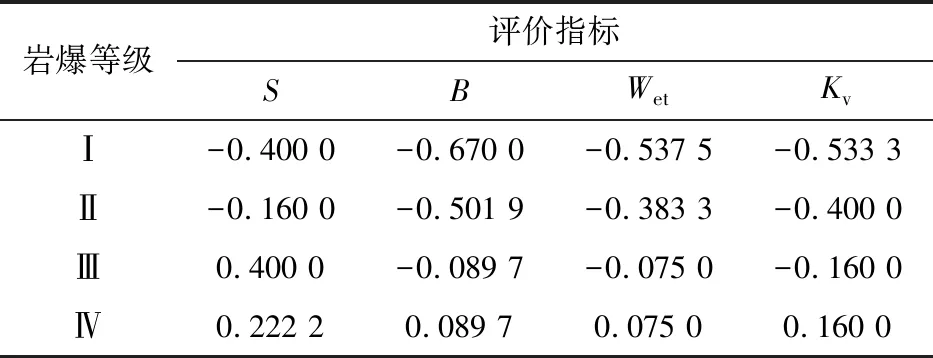
表4 样本1评价指标与危险性等级关联度

2.7 计算岩爆评价指标的权重

分别利用粗糙集理论、CRITIC法、乘法组合赋权法、博弈论综合赋权法计算各评价指标的权重,结果见表5。

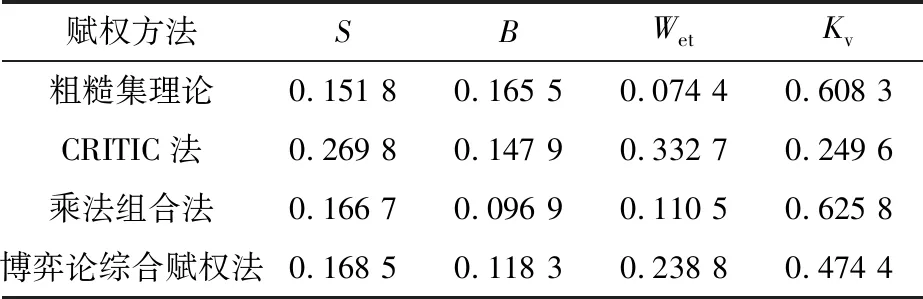
表5 各评价指标的权重

2.8 计算待评价指标与岩爆危险性等级的综合关联度及确定岩爆等级

第i个待评价指标关于岩爆等级j的综合关联度为

(21)

根据式(21)计算得到各样本与岩爆危险性等级的综合关联度,依据最大关联度准则判定岩爆等级,结果见表6。

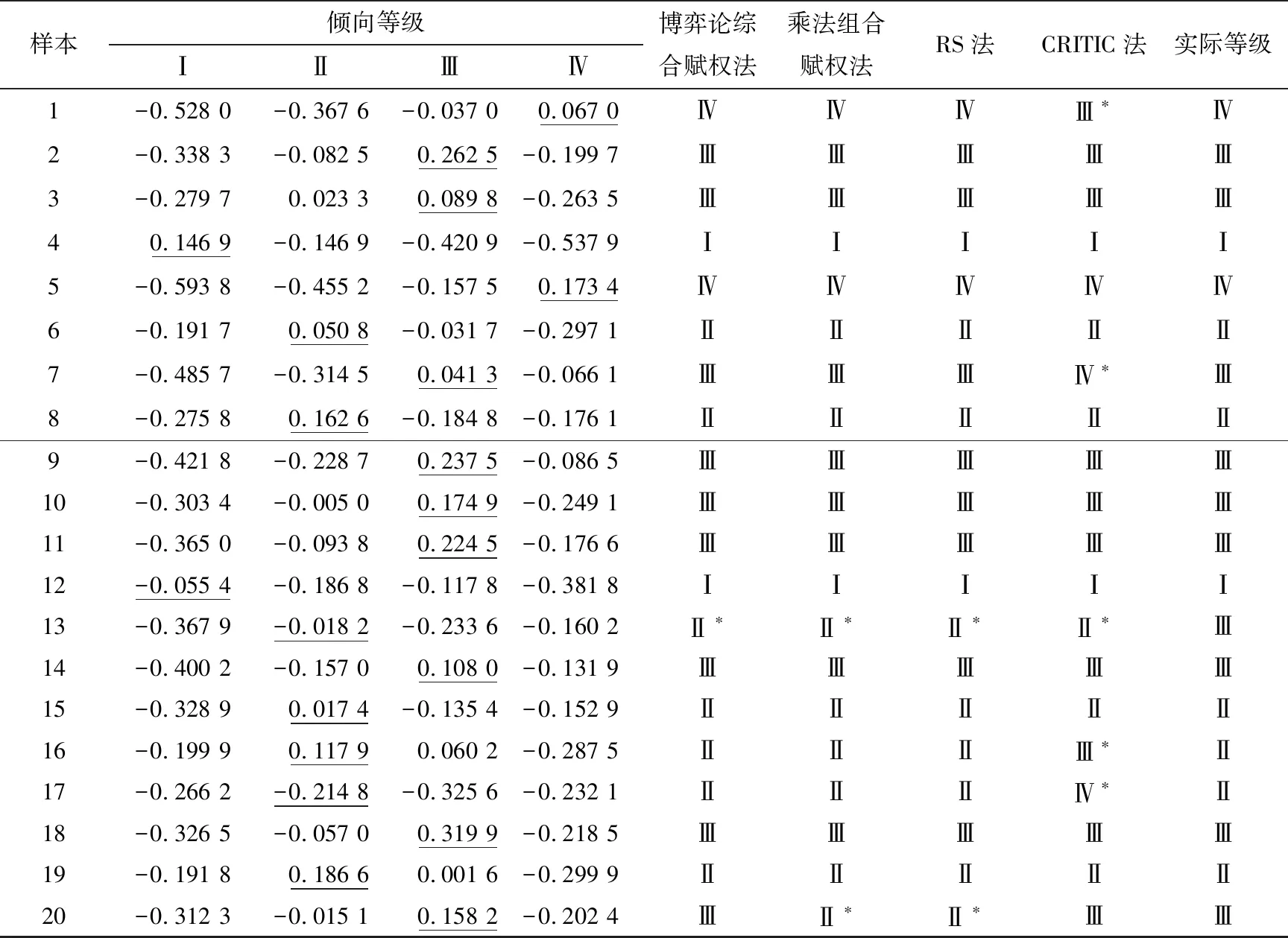
表6 不同赋权方法预测结果对比

表7 锦屏二级水电站引水隧洞实测数据

2.9 岩爆等级预测结果分析

依据最大关联度准则判定岩爆等级,基于博弈论综合赋权-可拓理论的岩爆预测模型准确率为95%,基于乘法组合、RS法与CRITIC法的岩爆预测模型准确率分别为90%、90%、75%,表明经过博弈论综合赋权后岩爆等级预测准确率得到了提高。

基于粗糙集理论的预测模型准确率为90%,基于CRITIC法的预测模型准确率为75%,两种赋权方法所得结果差异较大。粗糙集理论在计算过程中不需要先验知识且对数据的处理相对客观,该理论的出发点是直接对数据进行分析与推理,从而揭示潜在规律,但是数据处理过程较为“粗糙”,且并未考虑各评价指标之间的冲突性与变异性。基于CRITIC法的预测模型准确率较低,这是因为虽然CRITIC法考虑了指标间的冲突性与变异性,但是缺乏对各个指标与岩爆等级之间潜在规律的体现。故将两种赋权方法相结合,可以互为补充,提高赋权结果的可靠性。

不同综合权重计算方法的原理不同,所得到的赋权结果差异较大,直接影响岩爆等级预测模型的准确率。综合赋权所得到的权重为H=(0.168 5,0.118 3,0.238 8,0.474 4),L=(0.166 7,0.096 9,0.110 5,0.625 8),两组赋权结果具有较大差异,究其原因:乘法组合赋权在计算过程中某一因素所占权重会受到其他因素相乘与加和后的结果影响,计算过程不够科学合理,所得计算结果会明显突出或弱化部分影响因素。例如,乘法组合赋权结果中强度脆性系数(B)的权重远小于单一赋权方法所得到的权重,岩石完整性系数(Kv)的权重远大于其他赋权方法所得到的权重,而博弈论综合赋权有效避免了此问题,因而基于博弈论综合赋权-物元可拓的岩爆预测模型更为合理可靠。

3 工程应用

锦屏二级水电站位于四川省凉山州木里县境内,其地下硐室厂房多处于高山峡谷地带,地质条件复杂、地应力高,一般埋深1 000～2 000 m,最大埋深2 525 m,实测最大主应力值达到42.11 MPa;主要岩性为大理岩,岩石强度为60～75 MPa[19]。受到高-极高地应力与岩石强度较低的影响,该工程具备发生岩爆的地质条件。利用本文模型,以锦屏二级水电站引水隧洞实测数据为检验样本预测其岩爆等级。实测数据见表5。

根据粗糙集理论与CRITIC法获得单一权重,再使用博弈论进行综合赋权,得到的最优权重ω=(0.133 7,0.066 6,0.250 3,0.549 5),根据式(21)计算综合关联度,结果见表8。依据最大关联度准则可知,最终岩爆预测结果为Ⅱ级,属于轻微岩爆,预测结果与实际结果相符,进一步验证了本文模型的合理性与准确性。