熵权法和VIKOR算法在高职实训教学效果综合评价中的应用研究

尹帮治

摘要：熵权法和VIKOR算法相结合的方法对于提高实训教学效果综合评价的准确性和实用性具有重要意义。文章首先构建实训教学效果评价指标体系，然后收集了某高职院校三年间大数据分析与应用课程12个班级的实训教学评价数据，并进行了数据预处理和正态性检验。通过运用熵权法计算每个评价指标的权重，并结合VIKOR算法计算每个评价对象的群体效用值、个体遗憾值、效用比率和标准化得分，以此对每个教学班级进行科学合理的排序。研究结果表明，个体的遗憾值越低的评价对象或群体效用值越高的评价对象更有可能被排在前面。熵权法与VIKOR算法相结合，不仅可以避免主观判断或偏见对评价结果的影响，降低评价的误差和偏差，提高评价结果的全面性和可靠性，同时也可以量化各个评价因素的重要性，并得出各个评价对象的综合得分和排名，具有非常广泛的应用前景。

关键词：熵权法；VIKOR算法；实训教学；综合评价

中图分类号：G642      文献标识码：A

文章编号：1009-3044（2023）31-0166-05

开放科学（资源服务）标识码（OSID）

0 引言

高职实训教学效果评价研究的意义在于提升高职教育的质量和水平，确保学生能够掌握所需的实践技能和知识，为其未来的职业发展打下坚实的基础。

从目前已有的文献来看，多指标决策方法在教学效果综合评价中的应用研究主要有层次分析法、TOPSIS法和灰色关联度法。层次分析法优点能够直观地反映各指标间的重要性关系，易于理解和應用，但需要通过专家调查和判断确定权重，结果可能受到主观因素影响。TOPSIS法易于计算，对不同情况的动态调整敏感，但需要对各项指标进行归一化处理，结果的可靠性依赖于指标数据的质量。灰色关联度法能够量化评价指标间的关联性，但依赖于模型的合理性和可靠性，对因素间的关系假设不严谨可能导致评估结果不准确。

熵权法是一种基于信息论的权重确定方法，它可以避免主观因素的干扰，充分考虑了各指标之间的关联性。通过计算每个指标的信息熵，可以衡量指标的多样性和差异性，这有利于准确评价实训教学的质量。另外，该方法还可解决权重分配不合理、重点指标漏评等问题，使评价结果更加客观和准确。VIKOR法是一种以多指标评价为基础的决策方法，它具有综合性、灵活性和可操作性。该方法能够充分考虑不同指标之间的关系，并生成最优的决策方案。通过对指标的归一化处理和复杂度排序，VIKOR可以有效地评估实训教学效果的多重影响因素。因此，使用熵权法和VIKOR法进行高职实训教学效果评价，不仅考虑了评价指标之间的关联性和权重分配方法，还可以综合评估实训教学效果的各个方面。因此这种方法具有可行性，且有实际应用价值和推广意义。

1 熵权和VIKOR算法理论

熵权理论是一种用于多指标决策问题的判断模型，其基本思想是通过熵值来确定指标权重。其核心思想是根据信息熵理论，从熵的角度考虑多指标决策问题。它关注的是每个指标本身的信息量大小以及各指标之间的相关性，从而试图为每个指标赋予适当的权重。多准则妥协解排序法（VIKOR）能够在多个指标决策问题中选择最佳的方案。VIKOR理论对不同的指标进行综合分析，对于每个指标进行量化比较和综合考虑，以多指标决策为基础，综合考虑多个指标的影响。采用相对优先级排序的思想，将存在差异的指标进行比较，排除不必要的干扰因素。同时采用一种综合考虑各个指标权重的方法，基于各维度需求，权衡综合分析，制定最佳方案。

1.1 数据归一化处理

熵权法和VIKOR法都是多准则决策分析中常用的方法，它们可以结合不同的归一化方法进行决策分析。

熵权法通常适用于数据分布不均、数据范围差异比较大的场景，目的是消除指标之间的量纲和权值差异。在熵权法中，先将指标的最大值和最小值标准化到[0，1]范围内，然后根据熵值原理计算每个指标的权重。在这个过程中，可以使用多种归一化方法来将指标值标准化到[0，1]范围内，最大最小值归一化是其中一种常见的选择。

VIKOR法则是一种综合考虑加权和非加权指标的方法，可以解决多准则决策分析中的矛盾问题。VIKOR法也可以采用不同的归一化方法，主要是通过规范化、标准化等归一化方法将原始数据标准化到一定的范围内，消除各个指标间数据单位和量纲不同的影响。常用的归一化方法有最大最小值归一化和L2正则化等。

总的来说，最大最小值归一化更适合数据分布集中、范围明确的场景，L2正则化更适合处理大规模、高维数据，并且需要避免极端值对数据处理产生影响的场景。

设评价指标矩阵[A=aijm×n]，其中，m表示评价对象的数量，n表示指标属性的数量，i表示第i个评价对象，j表示第j个属性。评价指标分为效益型指标和成本型指标，效益型指标L2正则化处理如式（1） 所示，成本型指标L2正则化处理如式（2） 所示。

[Aij=aiji=1ma2ij，i=1，2，...，m;j=1，2，...，n]     （1）

[Aij=1aiji=1m1aij2，i=1，2，...，m;j=1，2，...，n]  （2）

效益型指标最大最小值归一化处理如式（3） 所示，成本型指标最大最小值归一化处理如式（4） 所示。

[Aij=aij-miniaijmaxiaij-miniaij，i=1，2，...，m;j=1，2，...，n] （3）

[Aij=maxiaij-aij  maxiaij-miniaij，i=1，2，...，m;j=1，2，...，n] （4）

1.2 熵权和VIKOR算法步骤

熵权和VIKOR算法步骤如下：

步骤1：计算评价指标的熵权

1） 计算评价指标的熵值

设[Ej]为第j个评价指标的熵值，根据熵值的计算公式，则[Ej]如式（5） 所示。

[Ej=-1lnni=1naij/i=1naijlnaij/i=1naij]   （5）

2） 计算信息效用值

设[Dj]为第j个评价指标的信息效用值，[Dj]的计算公式如（6） 所示。

[Dj=1-Ej]       （6）

3） 计算熵权

设[ωj]为第j个评价指标的熵权，[ωj]的计算公式如式（7） 所示。

[ωj=Dj/j=1mDj]   （7）

步骤2：计算正理想解和负理想解

设[f+j]为第j个评价指标的正理想解，[f-j]为第j个评价指标的负理想解，则[f+j]的计算公式如（8） 所示，[f-j]的计算公式如（9） 所示。

[f+j=1，j=1，2，...，n]    （8）

[f-j=0，j=1，2，...，n]    （9）

步骤3：计算群体效用值和个体遗憾值

设[S+i]为第i个评价对象的正理想解群体效用值，[R+i]为第i个评价对象的正理想解个体遗憾值，[S-i]为第i个评价对象的负理想解群体效用值，[R-i]第i个评价对象的负理想解个体遗憾值，则[S+i]的计算公式如（10） 所示，[R+i]的计算公式如（11） 所示，[S-i]的计算公式如（12） 所示，[R-i]的计算公式如（13） 所示。

[S+i=j=1nωjf+j-rijf+j-f-j，i=1，2，...，m;j=1，2，...，n]  （10）

[R+i=maxjωjf+j-rijf+j-f-j，i=1，2，...，m;j=1，2，...，n] （11）

[S-i=j=1nωjrij-f-jf+j-f-j，i=1，2，...，m;j=1，2，...，n] （12）

[R-i=minjωjrij-f-jf+j-f-j，i=1，2，...，m;j=1，2，...，n] （13）

由公式（10） 至公式（13） 可得出方案的群体效用值[Si]和个体遗憾值[Ri]，计算公式分别如式（14） 和式（15） 所示。

[Si=S+iS-i，i=1，2，...，m]     （14）

[Ri=R+iR-i，i=1，2，...，m]    （15）

步驟4：计算效用比率

设[Qi]为第i个评价对象的效用比率，计算公式如式（16） 所示。

[Qi=vSi-miniSimaxiSi-miniSi+1-vRi-miniRimaxiRi-miniRi] （16）

式（16） 中的[v]为群体效用和个体遗憾的调节系数，当[v]>0.5时，个体更加偏向于追求群体的最大效用，表现出风险偏好的态度。当[v]=0.5时，个体更加注重平衡群体的最大效用和最小遗憾，表现出风险均衡的态度。当[v]<0.5时，个体更加注重群体的最小遗憾，表现出风险厌恶的态度。

步骤5：计算标准化得分

设[Score_Qi]为第i个评价对象的标准化得分，计算公式如式（17） 所示。

[Score_Qi=Qi-ave（Q）stv（Q），i=1，2，...，m]  （17）

式（17） 中[ave（Q）]表示m个评价对象的效用比率[Q]的均值，[stv（Q）]示m个评价对象的效用比率[Q]的标准差。

1.3 评价对象排序

评价对象的最终排序判断依据如下：

条件一：[Qx-Qy≥1/n-1]

条件二：[Sx]>[Sy]或[Rx]>[Ry]

其中，Q值从小到大排序，x为Q值排序高的评价对象，y为Q值排序次之的相邻评价对象。若排序对象同时满足条件一和条件二，则被确定为最稳定、最优排序解；若排序对象只满足条件一，则被认定为折中排序解；若排序对象只满足条件二，表明评价对象个体的遗憾值或群体的效用值对最终排序有较大影响。本文评价对象排序依据如下：若排序对象同时满足条件一和条件二，采用Q值的大小确定排序对象的最终排序结果，否则采用Q值的标准化得分确定排序对象的最终排序结果。

2 构建实训教学效果评价指标体系

研究众多文献，结合笔者在高职院校的教学工作经验，分别从参考文献的高职实训教学效果评价指标体系中的实践教学设置评价、实践教学方法评价、实践教学过程评价、教师素质评价、实践教学效果评价等五个一级指标中，提取了12个二级定量指标用于本文的教学效果综合评价。

1） 学生对教师教学设计的满意率（A1） ，该指标是指学生对教师教学设计的满意率指的是学生对教师教学计划、教案、教材等方面的满意度，主要是从学生的角度出发，评价教师教学设计是否符合学生的学习需求，是否具有可操作性、实用性和科学性等。

2） 学生对教师教学方式的满意率（A2） ，该指标是指学生对教师教学方式的满意率是指学生对教师在教学过程中所采用的教学方式的评价，包括教师的授课方式、教学技能、教学手段和教学语言等方面，主要是从学生的角度考虑教师的教学方式是否能够促进学生学习效果的提高，是否符合学生的学习需求和特点。

3） 学生对教师教学内容的适应率（A3） ，该指标是指学生对教师教学内容的适应率指的是学生对教师所讲授的课程内容的适应程度，评价教师的教学内容是否与学生的知识水平相符、是否具有实用性和可操作性等。

4） 学生对教师教学指导的满意率（A4） ，该指标是指学生对教师教学指导的满意率是指学生对教师在教学过程中所给予的学习辅导和指导的评价，主要是从学生的角度出发，评价教师的指导能力是否足够专业、具有针对性和实效性等方面。

5） 学生对教师教学管理的满意率（A5） ，该指标是指学生对教师教学管理的满意率指的是学生对教师在教学过程中所做的教学管理措施的评价，主要考虑教师是否能够合理安排课程，是否對学生的学习情况进行了恰当的跟踪和管理等。

6） 学生对教师教学态度的满意率（A6） ，该指标是指学生对教师教学态度的满意率是指学生对教师在教学过程中所表现出的教学态度、作风和品质的评价，主要考虑教师是否通过自身的示范来引导学生的学习，是否对学生有耐心和关心等。

7） 学生对教师教学能力的满意率（A7） ，该指标是指学生对教师教学能力的满意率指的是学生对教师在教学过程中所表现出的教学能力和水平的评价，主要考虑教师是否具有教学能力和专业能力，是否能够培养学生的能力和技能等方面。

8） 实训成果创新率（A8） ，该指标是指实训项目创新率指的是学生在实际操作实训项目时，能够在过程中提出自己的创新思路和想法，发掘新的解决问题的方法和途径，主要衡量学生的独立思考和创新能力。

9） 实训考试成绩优良率（A9） ，该指标指学生在实训过程中所涉及的技能应用考试中，取得成绩优良（例如A，B级）的比例，主要评价学生的实际操作技能水平和应用能力。

10） 获得职业资格证书比率（A10） ，该指标是指获得职业资格证书比率是指在高职实训教学过程中，学生取得国家或地方职业资格证书的比例，体现学生所学的实际应用价值和职业素养水平。

11） 实训项目完成时间比率（A11） ，该指标是指实训项目完成时间比率是指学生在实际操作实训项目时，完成实训任务所花费的时间比例，主要是从时间管理的角度衡量学生实际操作的效率和质量，适当地压缩完成时间，可以更好地提高实训效果。

12） 学生实训缺勤率（A12） ，该指标是指学生因为主观或客观原因，在实训教学期间未能按时参加或完成规定的实训课程或实践活动的比例。

从上述评价指标的类型可以看出，指标A1至A10（共10个指标）属于效益型指标，其值越大越好；指标A11和A12（共2个指标）属于成本型指标，其值越小越好。

3 综合评价应用研究

3.1 获取研究数据

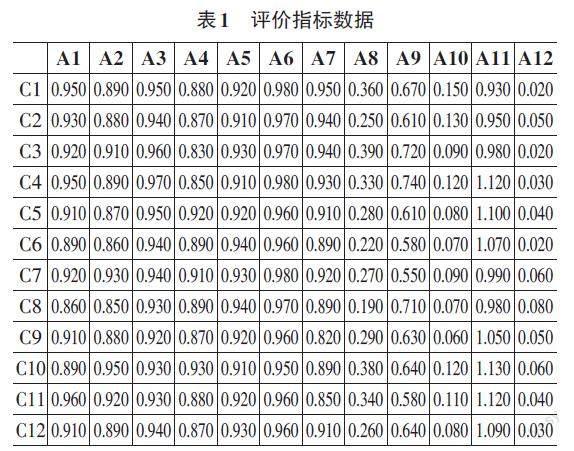
基于上述12个教学效果评价指标，从某高职院校教务处，获取了大数据技术专业大数据分析与应用课程近三年的教学效果评价数据，共12个教学班级，分别用“C1”至“C12”表示。C1至C4是2022级大数据专业的教学班级，C5至C8是2021级大数据专业的教学班级，C9至C12是2020级大数据专业的教学班级。研究数据经过清洗、去重、缺失值处理等相关数据预处理工作，最后汇总如表1所示。

3.2 数据正态性检验

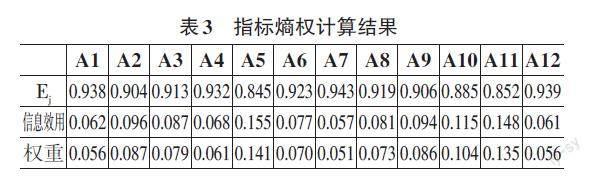
对数据进行正态性检验是为了检查这些数据是否符合正态分布。如果数据服从正态分布，那么在进行熵权计算和VIKOR法计算时，对数据进行标准化的结果更可靠和准确。同时，如果数据不符合正态分布，则需要进行针对性的数据转换或使用非参数方法进行计算，以更准确地评估各指标在决策中的重要性和综合得分，进而提高决策的可信度和稳定性。因此，对数据进行正态性检验可以帮助选择适当的数据分析方法，并确保所得出的结论是可靠的。对表1的数据进行正态性检验的结果如表2所示。

从表2可以看出，由于样本N < 5000，故而采用S-W检验。变量A1至A12的显著性P值均大于0.05，水平不呈现显著性，不能拒绝原假设，因此数据都满足正态分布。

3.3 计算评价指标的熵权

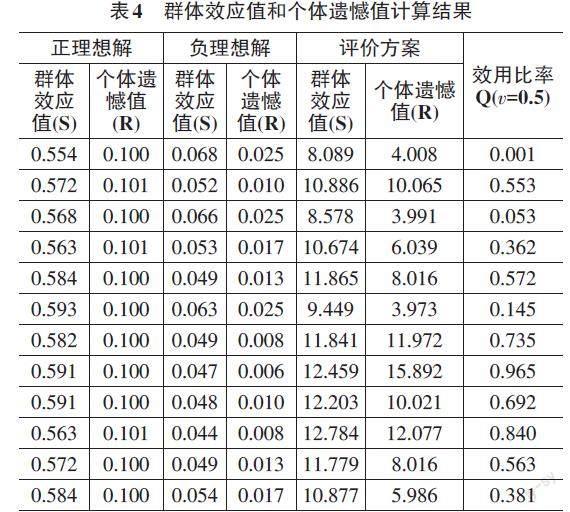
运用公式（1） 至（7） 计算的结果如表3所示。

从表3可以看出，熵权法的权重计算结果显示，A1的权重为5.639%、A2的权重为8.724%、A3的权重为7.918%、A4的权重为6.148%、A5的权重为14.06%、A6的权重为7.007%、A7的权重为5.148%、A8的权重为7.348%、A9的权重为8.561%、A10的权重为10.433%、A11的权重为13.454%、A12的权重为5.56%，其中指标权重最大值为A5（14.06%） ，最小值为A7（5.148%） 。

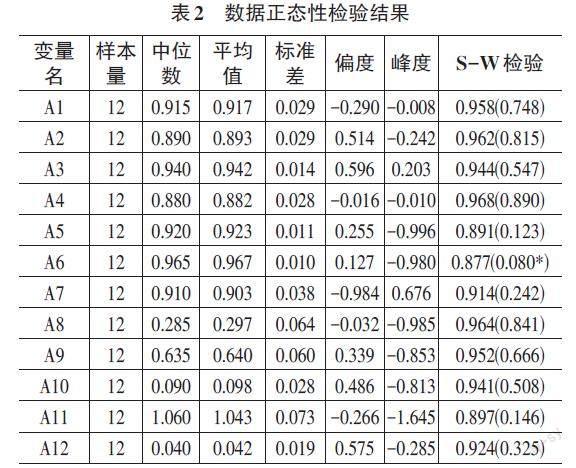
3.4 计算群体效应值[Si]、个体遗憾值[Ri]和效用比率[Qi]

调节系数[v]=0.5，运用公式（8） 至（15） 计算的结果如表4所示。

3.5 研究结果

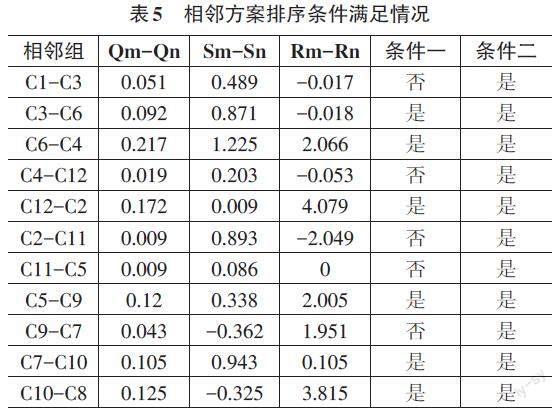
效用比率[Qi]的均值初值排序对应的评价对象排序结果如下：C1 > C3 > C6 > C4 > C12 > C11 > C5 > C2 > C9 > C7 > C10 > C8，相邻两个方案的Q值之差、R值之差与S值之差的计算结果以及排序条件满足情况如表5所示。

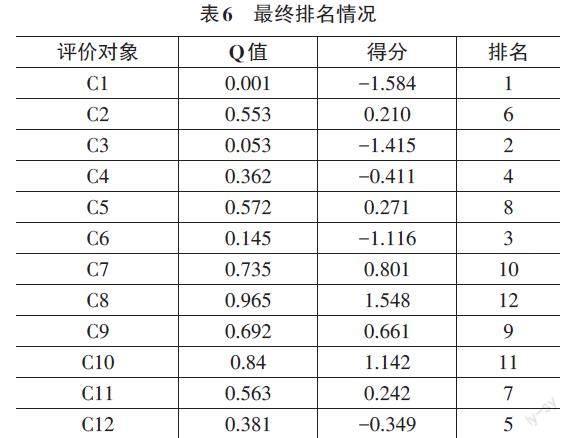
从表5可以看出，评价对象C3与C6、C6与C4、C12与C2、C5与C9、C7与C10、C10与C8同时满足条件一和条件二，这些评价对象之间的排序确定为最稳定、最优排序解；其他相邻组的只满足条件二，因此需要根据公式（17） 计算其标准化得分，利益比率值（Q）的均值为0.489，标准差为0.308，计算结果及最终排结果如表6所示。

基于上述的研究结果，可以从各个班级的实训整体效果和纵向比较来分析。

1） 实训整体效果

学生对教师教学方面的满意度： C1班级在学生对教师教学设计的满意率、学生对教师教学内容的适应率、学生对教师教学能力的满意率方面都得到了高分，因此在综合起来的评价中获得了第一名。而C8班级在所有方面得分都比其他班级低，说明这个班级的教学效果较差。

实训成果和考试成绩： C4班级在实训成果创新率、实训考试成绩优良率等方面得分较高，说明这个班级的学生在实际的实训内容中表现优秀。而C10班级在实训项目完成时间比率方面表现较差，说明这个班级的学生需要更加努力地完成实训任务。

学生的实习缺勤率： C1、C3、C5、C9、C11、C12班级的学生实习缺勤率均较低，说明这些班级的学生有较强的学习自觉性和责任心。而C2、C4、C6、C7、C8、C10班级的学生实习缺勤率相对较高，说明这些班级的学生可能需要更严格的教学管理措施。

2） 纵向比较

首先，从整体水平角度来看，2022级的教学班级在大数据实训教学中总体表现比2021和2020级的班级好。2022级的教学班级中，C1排名第一，表现最好，排名第六的C2与排名第四的C4表现也比较出色；C3排名第二，但与C1的差距很小。可以看出，整体上2022级的教学班级的表现都相对较好，表现最弱的C2也排在第六位。

其次，从年级角度来看，2022级的教学班级与2021级相比，整体表现更好，而与2020级相比，整体表现也更好一些，排名前四的班级都属于2022级的教学班级。可以看出，该大学的大数据实训教学在逐年优化，加强了对学生的指导和管理，2022级的教学质量得到了进一步提高。

最后，从具体班级角度来看，虽然整体上2022级的教学班级表现较好，但C2在班级中的排名却比较靠后。这可能是班级自身的原因，如学生学习态度不够积极、实训环节中可能存在问题等。教学管理者可以重点关注这些班级差异，调整教学安排和管理方式，确保每个班级都能够得到更好的教育。

4 研究结论

1） 个体的遗憾值越小的评价对象，或群体效用值越高的评价对象，排在前面的概率越大。具体来说，遗憾值小的评价对象说明其实现的效益和效果非常接近个体最优解，因此被认为更优秀；而群体效用值高的评价对象能够更好地满足群体利益，因此也更有可能优先被选择。

2） 熵权法和VIKOR算法相结合可以提高评价的可靠性和全面性，但是需要开展详细的评价过程和敏感性分析，减小人为因素对评价结果的影响，保证评价结果具有更高的可信度、实用性和参考价值。

3） 熵权法和VIKOR算法可以同时考虑各个评价因素，对其重要性进行量化，并且可以计算出各个评价对象的综合得分和排名，这体现了该方法的全面性；以熵权法和VIKOR算法为基础进行多属性综合评价可以帮助规避主观判断带来的问题，并降低评价的偏见度和误差，这体现了该方法的可靠性。因此，熵权法和VIKOR算法可以根据各个评价对象的实际情况进行评价，评价结果具有实际意义和指导意义。本文提出的融合熵权法和VIKOR算法可以拓展应用至其他以多属性决策法建构的评估模型中，有广泛的应用前景。

参考文献：

[1] 周小琴.五年制高職实训教学过程质量评价研究[J].湖北开放职业学院学报，2022，35（7）：137-139.

[2] 曾凡龙，倪静，王钰华.基于熵权-VIKOR及AGA-BP模型的企业绩效评价研究——以我国上市物流企业为例[J].上海理工大学学报，2022，44（1）：94-102.

[3] 王志愿，闫磊磊，邓迎寅，等.基于熵权与VIKOR方法的设计方案评价与优选[J].机械设计，2022，39（2）：154-160.

[4] 尹夏楠，朱莲美，鲍新中.基于VIKOR方法的高新技术企业成长性评价[J].财会通讯，2015（34）：38-41，4.

[5] 徐婷婷.面向工作过程的职高计算机专业课程教学评价体系研究[D].上海：上海师范大学，2014.

[6] 张春艳，张春霞，胡海星.高职实训教学质量评价指标体系研究[J].吉林省教育学院学报（中旬），2014，30（3）：112-113.

【通联编辑：王 力】