基于弹性核凸包张量机的高速球轴承故障诊断方法
2023-12-24谢忠敏张清丰
谢忠敏,孙 罡,张清丰
(1.成都农业科技职业学院 机电信息学院,四川 成都 611130; 2.电子科技大学 信息与通信工程学院,四川 成都 611731)
从本质上来看,轴承故障智能诊断过程可划分为模式识别类别,处理数据时采用反向传播神经网络或支持向量机实现[1-2]。在进行故障诊断模型构建时通常应用深度学习算法,自适应学习及初始信号特征参数提取均在此过程中产生[3]。模式识别有效性及轴承故障特征提取精度都会对识别精度产生较大影响[4-5]。从信息数据收集及获取情况来看,传统时频域分析技术具有一定局限性,高速球轴承特征参数通常可通过时频图像来表征,反映轴承初始振动信号[6-7]。
相关方面的研究吸引了很多的研究学者,做出了突出的贡献。于春霞等[8]设计完成了能有效提升重构信号精度的AP-FBSOMP 组合算法,为优化正交匹配追踪(OMP)算法,结合K奇异值分解(KSVD)和信号分块自适应(AP),结果显示从分块压缩感知(CS)重构性能提升效果来看,轴承微弱故障信号更显著。马怀祥等[9]提出的滚动轴承故障诊断方法可实现高达99%测试集准确率,该方法的理论基础是极端梯度提升(XGBoost)以及卷积神经网络(CNN),经交叉验证该模型可行性较高。王勉等[10]将提出的滚动轴承故障诊断方法可支持向量机(SVM),同时分析并对比时移多尺度散布熵(TMDE)与MDE 的诊断精度,验证TMDE 的效果更佳。史红梅等[11]提出的旋转机械故障方法为动态加权多尺度残差网络型,标定数据利用特征通道,相对较为新颖,该算法有效性经大量数据集试验后得到验证。
由于样本点决策贡献度在超平面优化分类过程中所使用的方法考虑到,因而导致测试集分类精度偏低。对此本文在进行时频分布建立时选用连续小波转换方法,在技术成熟度方面相对较高,特征集的建立则依据灰度共生矩阵实现,类别判断模型构建时用正负概率估计代替分类器距离并输出。
1 弹性核凸包张量机
H为实数向量空间,空间内位置坐标表示为x,那么位于空间H内的样本集X={x1,x2,…,xn}的凸集C的表达式为
式中:αi为样本i的组合系数。
凸包组合系数上下限的设置与样本数n和弹性因子λ∈(1,∞)相关,弹性凸包算法可表示为
样本集X弹性凸包可通过简单推导得到,按照下列形式进行等价计算:
式中:x'i为在向量xi方向的新样本。样本集宽松估计及凸包紧致可通过λ参数调整实现,才能确保凸包弹性可变。
弹性凸包分类采用最优超平面方法完成,才能保证正负类样本凸包在处理过程中获取的间隔最大。当然分别按的条件严格限制每个正类样本集、负类样本的样本点,以|w,x|表示分类超平面法向量,x表示样本点,b代表偏置。2个凸包最近点的求解即为分类超平面:
上述算法为凸二次规划,为确保线性可分成功代替不可分情况,在求解过程中选用标准优化算法,映射核空间则由核函数实现。本文构建的核函数为高斯核函数:
式中:σ为函数径向区间的高斯核函数调节宽度。
根据式(5)得到的最优解是α*,之后利用α*确定法向量w*与偏置b*:
2 特征提取步骤
本文采用弹性核凸包张量机以及纹理特征来诊断高速球轴承故障,具体步骤如下:先通过加速度传感器采集获得高速球轴承运行过程的振动信号,再对实施连续小波变换获得小波时频曲线;其次利用时频图灰度共生矩阵建立纹理特征,将其分成训练与测试集合;最后利用训练弹性核凸包张量机模型来识别测试集样本,实现故障的快速诊断。以下给出了特征提取的具体步骤:
步骤1故障信号通常会产生强烈冲击,考虑morlet小波所具备的冲击适应能力[15],利用morlet小波建立小波基函数来达到连续小波转换的效果,形成时域振动信号曲线,再把时频图转化成像素精度为256×256的灰度图像。
步骤2划分上述时频图得到像素精度为128×128的4个图像,高频与低频区的数量都是2个。
步骤3依次求解时频图各区域不同方向对应的灰度共生矩阵。
步骤4对各方向特征进行综合分析,再队上述各方向形成的纹理特征进行计算,利用均值与方差组成32维特征向量,将其表示成TFIT。
3 实验分析
选取的测试对象为6205-2RS 型深沟球轴承,按照48 kHz 标准对采样频率进行控制,样本种类共计1 400 个,每个样本的采样点有16 000 个。轴承故障类型具体可参考表1。

表1 轴承数据样本Tab.1 Bearing data sample
依次利用数据集A、B 完成故障种类及程度的识别,测试对比不同分类方式的故障识别情况。高斯核参数σ以及弹性因子λ作为优化弹性核凸包张量机的两个指标。为保证达到最优条件,网格参数搜索选用5 折交叉方法,σ搜索区间介于2~28,步长保持0.2,λ搜索区间20~24,对应步长0.2。
两种分类器(支持向量机、初始弹性凸包)在网格搜索算法的支持下完成参数设置。故障识别精度具体可参考表2 数据,采用五折交叉测试方法对最优参数进行20 次连续测试,其中最优参数由网格搜索获得,此过程中分类器及各特征集共同组建模型。

表2 识别准确率Tab.2 Identification accuracy rate
相比于初始弹性凸包分类方式,对比分类器以及固定特征得出,应用本文方法能更准确且更快速地识别故障。同时,与传统时频特征相比,时频图纹理特征在故障识别性能方面表现更优,准确率更高。另外在识别故障的过程中,ESTC 在识别数据集A 分类模型方面展现出更优越的性能,准确率及精度均高于TTF。上述结果验证高速球轴承故障特征的保留更具充分和完整,时频域两种数据均包含在时频图像当中。
为了观察对比泛化效果,需要对弹性核凸包张量机开展相应的测试,同时为增强说服力,在分析数据集B 故障特征时参考时频图纹理特征。选定的训练集包含多种样本,在此基础上测试剩余样本,图1 为测试次数达20 次后获取的分类结果,测试为随机独立方式。

图1 识别准确率与训练集占比关系Fig.1 Relation between recognition accuracy and training set proportion

图2 机械故障试验台Fig.2 Mechanical failure test bed
观察图1 发现,即使仅有少量训练样本存在于ESTC 特征中,准确率却能达到93%以上,依然较高;弹性核凸包张量机在只剩10%训练集样本时,测试集准确率依然能保持在95%,从该数据能验证在泛化性能方面,弹性核凸包张量机表现十分优异。另外还发现,分类精度在弹性核凸包张量机对应的识别精度曲线中获得最优值。
高速球轴承运行参数则通过旋转机械故障测试获取。选取的测试对象为23030CC 型高速球轴承,测试台架结构图如图3 所示,按照0.2 mm 的标准设置切割深度,并对不同部位的故障采用激光进行切割,包括滚动体、外圈、内圈。采样频率、电机转速依次设置为10 kHz、1 440 r/min,样本参数具体数值可参考表3。

图3 识别准确率与训练集占比关系Fig.3 Relation between recognition accuracy and proportion of training set

表3 轴承数据样本Tab.3 Bearing data samples
弹性核凸包张量机故障特征包括时频纹理参数,按照最佳值λ=1.740,σ=2.212 9 设置分类器参数。各个模型的测试时间及训练记录均需在测试阶段完成。测试系统基于Matlab2 建立,选取Intel Xeon E3 作为处理器,表4 给出具体的测试数据。
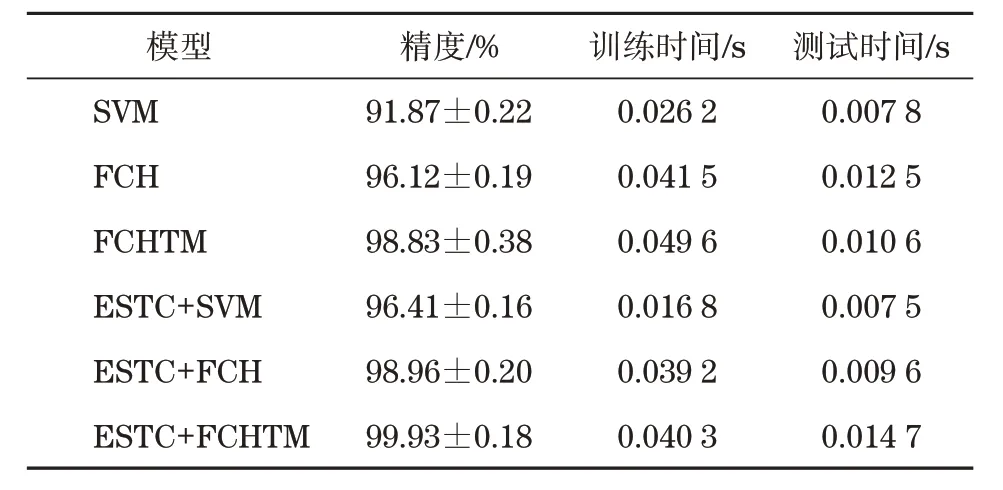
表4 识别准确率及运行时间Tab.4 Recognition accuracy and running time
分析表4 数据得出,在准确率方面弹性核凸包张量机确实展现出较佳的性能优势,相比于原始弹性凸包,2个特征集的分类精度均更高,并且在测试和训练时长方面,相比于SVM 和初始弹性凸包均得到延长,且延长时间小于0.1 s,严格控制在实时诊断标准范围之内。采用随机方法选取训练集样本量进行20 次独立准确率测试,结果如图3 所示。经观察对比,发现在识别精度和分类性能方面,弹性核凸包张量机均展现出较强的优越性,并且适当增加训练样本还能有所提升。当训练集中样本比例为10%时,测试弹性核凸包张量机特征集准确率,结果显示高达96%,明显高于初始弹性凸包。通过分析这些数据,得出相比于原始弹性凸包,在对数据集进行分类处理时选用弹性核凸包张量机能有效提高故障识别效率,表现优越的故障识别检测性能。
按照7.5∶2.5 比例选定训练集与测试集划分数据集B 与C,目的是判断FCHTM 鲁棒性。首先是在当前训练集中新增2 个样本,样本源于其他训练集;然后为验证测试集的准确率,需要训练样本,采用随机方法对样本进行20 次的独立测试,具体数据见表5。
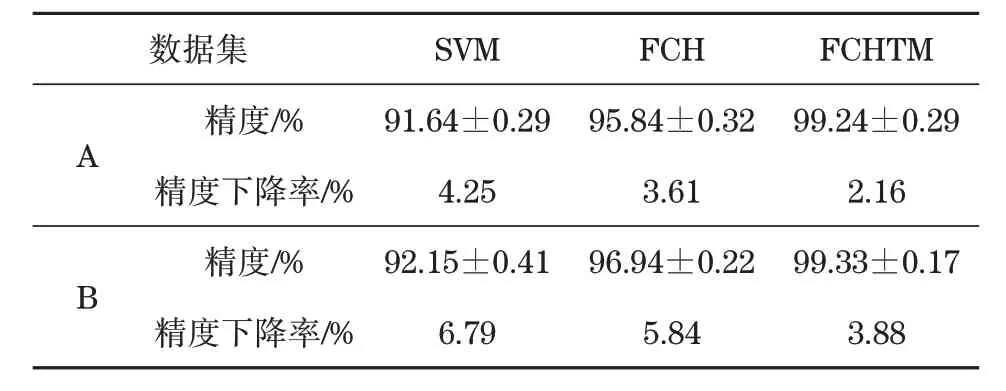
表5 鲁棒性测试结果Tab.5 Robustness test results
训练集与测试集采用五折交叉测试完成20 次测试的结果可参考表2与表4,划分比值依然为7.5∶2.5。对比不同分类方式准确率数值,最终发现弹性核凸包张量机表现最佳。离群点影响强弱情况可通过识别精度下降率数值获取,在鲁棒性和抗噪性表现方面弹性核凸包张量机的优势更显著。
4 结论
(1) 采用随机方法选取训练集样本量进行准确率测试,发现在识别精度和分类性能方面,弹性核凸包张量机均展现出较强的优越性,并且适当增加训练样本还能有所提升。
(2) 训练集与测试集划分为7.5∶2.5 开展分类准确率分析,发现弹性核凸包张量机表现最佳,在鲁棒性和抗噪性表现方面弹性核凸包张量机的优势更显著。
