基于突变理论的两断层中间区域重叠顶底板稳定性分析

2023-12-23李弘博陈俊智陈明清王子航

矿冶 2023年6期

李弘博陈俊智陈明清王子航王昊

(昆明理工大学国土资源工程学院，昆明 650093)

采空区失稳是一种典型的非线性变化过程，出现于20世纪七十年代的突变理论对于分析这种非线性问题具有较好的效果[1-2]。

在使用突变理论分析矿山采空区支撑系统稳定性方面，国内外学者已取得了一定的成果。QIN等[3]建立了煤矿的顶板—矿柱支撑系统力学突变失稳模型，给出了煤矿采空区失稳的判据及位移突变计算公式。赵延林等[4]建立了基于突变理论的采空区重叠顶板稳定性强度折减法，提出了采空区重叠顶板安全系数的概念。徐晓鼎等[5]将矿柱破坏分为弹性核区与屈服区，构建了石膏矿的顶板—矿柱支撑系统力学突变失稳模型，给出了石膏矿采空区失稳的判据。姜立春等[6]发现含结构面矿柱会沿结构面破坏，因此将矿柱划分为结构面上部弹性核区与结构面下部屈服区，构建了含结构面的顶板—矿柱支撑系统力学突变失稳模型，给出了含结构面的矿柱失稳判据。

对文献进行总结可发现目前使用较多的采空区顶板—支护系统力学模型分别为：将顶板视为固支梁，分析支撑系统或顶板本身破坏[7-9]；将系统视为安装在柱上的三铰拱，分析顶板破坏[10-11]；将矿柱视为弹簧，顶板视为梁，分析顶板破坏[12]。但目前对顶板完全破坏阶段研究较多，对顶板处于拱冒型破坏阶段的研究较少。

同时在使用突变理论建立包含多个影响因素的采空区稳定性综合评价与失稳预测模型方面也取得了一定成果[13-14]，说明突变理论可以有效分析影响采空区稳定性的多个因素。

云南某铅锌矿矿体绝大多数赋存于矿区内F1断裂与F2断裂中间区域，该组断裂在矿区内控制长度为3 730 m，向矿区外南东-北西方向继续延伸，延伸长度大于5 300 m。该组断层垂直断距高达600～900 m，破碎带宽20～60 m。受该组特殊断层影响，该矿山内采场基本处于该组断层中间区域。受特殊地质情况影响，该矿山采场存在大量处于两断层中间区域的重叠顶底板。计算重叠顶底板合理厚度对矿山安全高效开采具有重大意义。因此，开展分布于两断层中间区域的采空区失稳机理研究，具有重要的理论和工程意义。

1 系统力学模型

1.1 采空区顶板结构破坏特征

对矿山采空区进行调查后发现：采空区重叠顶底板主要破坏形式表现为上部采空区底板先发生底鼓现象，随后下部采空区顶板发生局部拱冒型破碎，在拉应力作用下，重叠顶底板拱冒型破坏范围不断扩大，最终重叠顶底板发生整体冒落型破坏。

根据矿山实际地质条件及其开采方式，绘制如图1所示的矿山实际情况模型，考虑到实际情况模型较复杂，因此将采空区及其周围区域简化为如图2所示的简化模型。

图1 原始矿山立体模型

1.2 采空区简化模型数值模拟方案确定

建立与简化模型对应的数值模拟模型，分析有无断层对采空区顶板应力变化的影响。模型上部采空区顶板埋深为310 m，上下采空区参数一致，均为高25 m、长60 m、宽30 m，两采空区重叠顶底板厚度10 m。在两采空区重叠顶底板两侧及中部按不同高度共设置27个应力监测点，分析开挖形成采空区后，有无断层对顶板两端承受压应力的影响。

计算模型如图3所示：ZG_001与ZG_004为分布于矿体两侧的断层，ZG_002、ZG_003与ZG_005为围岩，ZG_006与ZG_007为矿体。计算方案1为该模型内无断层，即ZG-001与ZG-004采用下盘围岩参数计算；计算方案2为模型内存在两条断层，即ZG-001与ZG-004采用断层参数。计算用参数如表1所示。

表1 岩体力学参数表

图3 数值模型

将数值计算模型x方向与y方向位移与速度场均固定为0，将数值计算模型底面的位移与速度场固定为0，数值计算模型顶面不做约束，在模型顶面施加竖直向下大小为8.06 MPa的均布荷载代替计算模型上部覆岩产生的压应力。

1.3 数值模拟结果分析

1)应力分析

对计算方案1的开采后采空区重叠顶底板Z向应力云图(计算结果如图4所示)与计算方案2的开采后采空区重叠顶底板Z向应力云图(计算结果如图5所示)进行对比分析，可发现与矿体两侧不存在断层的情况相比，矿体两侧存在断层的情况下，采空区重叠顶底板内受到的拉应力更大，且采空区重叠顶底板内受到拉应力影响的范围更大。

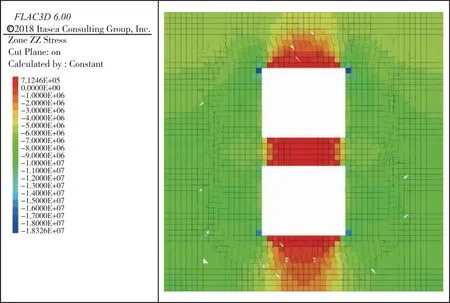
图4 计算方案1采空区重叠顶底板Z向应力云图

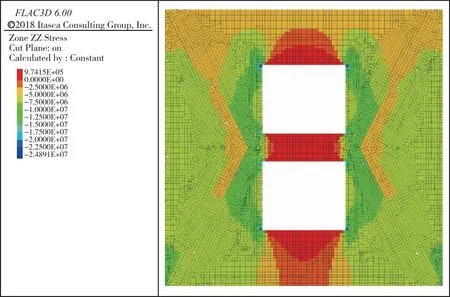
图5 计算方案2采空区重叠顶底板Z向应力云图

2)位移分析

对计算方案1的开采后采空区重叠顶底板X向位移云图(计算结果如图6所示)与计算方案2的开采后采空区重叠顶底板X向位移云图(计算结果如图7所示)进行对比分析，可发现与矿体两侧不存在断层的情况相比，矿体两侧存在断层的情况下，采空区重叠顶底板内水平方向位移量相对更大，且采空区重叠顶底板内水平方向位移涉及范围相对更大。

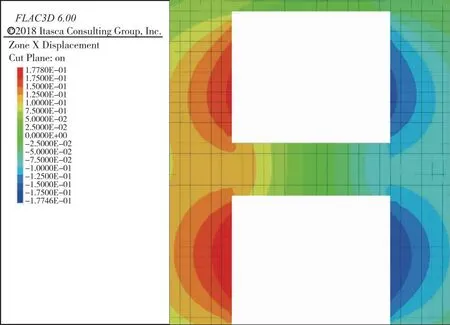
图6 计算方案1采空区重叠顶底板X方向位移云图

图7 计算方案2采空区重叠顶底板X方向位移云图

综合以上分析结果可知：在断层影响下，重叠顶底板内受到的拉应力与水平方向位移均更大。

2 采空区顶板部分失稳的非线性力学特征

2.1 采空区顶板系统力学模型构建

本文主要分析重叠顶底板发生拱冒性破坏阶段稳定性。因此，假设空区周围岩体为刚性，将顶板岩层视为固支梁，顶板岩梁弯曲变形以弹性破坏为主[15]，破坏发生在一个平面内，服从平截面假设。同时假设顶板未破坏时，发生弯曲伸长后，顶板厚度随之减小。采空区顶板力学模型可简化为如图8所示的力学模型。图中：L为采场跨度，m；h为采场顶板厚度，m；q为采场顶板所承受由自重及上部岩体压力产生的垂直均布荷载，kPa；p为采场顶板岩梁受到的侧向水平推力，kN；F为采场顶底板岩梁受到的拉应力(假设该拉应力集中作用于岩梁两侧与岩壁的交点处)，MPa。

图8 固支梁力学结构模型

2.2 顶板系统总势能函数

由力学模型可知[16]，系统总势能由顶板岩梁的弯曲应变能、侧向水平荷载做功、垂直均布荷载产生的势能、下部产生的垂直向上作用于岩梁与围岩连接处的集中应力做功组成。

设顶板岩梁在中部产生的最大挠度为u(单位：mm)。

根据边界条件：

(1)

顶板岩梁的挠曲线方程可写为：

(2)

式中：x为顶板岩梁端点到未变形轴线上任意点的长度，m；L为顶板岩梁长度，m；f(x)为顶板岩梁在x处对应的挠曲线方程；u为顶板岩梁在中部产生的最大挠度，mm。

顶板岩梁的弯曲应变能V1为：

(3)

(4)

(5)

式中：K(x)为岩梁弯曲后，以岩梁左侧端点为原点的挠曲线在x点处的曲率；E为顶板岩梁的弹性模量，GPa；D为顶板岩梁抗弯刚度，GPa；μ为泊松比；h为顶板岩梁厚度，m。

顶部岩梁两侧水平荷载做功V2为：

(6)

式中：P为顶板岩梁受到的侧向水平推力，kN。

顶部垂直均布荷载产生的势能V3为：

(7)

式中：q为采场顶板所承受由自重及上部岩体压力产生的垂直均布荷载，kPa。

下部产生的垂直向上作用于岩梁与围岩连接处的集中应力做功V4为：

V4=Fε

(8)

式中：F为采场顶底板岩梁受到的拉应力，MPa；ε为采场顶板岩梁厚度变化量，m。

顶板岩梁厚度变化ε为(顶板岩梁在应力作用下会发生如图9所示的微量形变)：

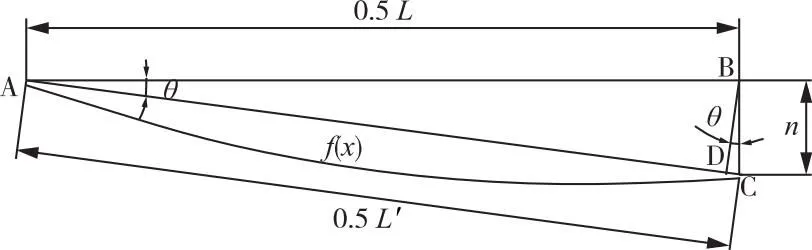
图9 顶板岩梁长度变化示意图

因顶板岩梁变化较小，因此挠曲线函数f(x)一半的长度可近似等同为AC段的长度。

已知在θ较小时，θ≈tanθ≈sinθ，因此由三角函数可推知：

(9)

式中：L′为顶板岩梁变形后总长度，m。

假设顶板岩梁变形处于线弹性阶段，因此：

Lh=L′h′

(10)

式中：h′为顶板岩梁变形后的厚度，m。

对h′进行泰勒展开，同时略去过小项，最终可得顶板岩梁厚度变化为：

(11)

所以，下部产生的垂直向上应力做功V4为：

(12)

所以，将上述各势能函数带入上式，最终顶板岩梁支撑系统势能函数表达式为：

V=V1-V2-V3-V4=

(13)

(14)

因此可转化为尖点突变模型的标准势函数形式：

(15)

式中：x为状态参量，a、b为控制参量，说明该顶板岩梁支撑系统稳定性问题符合尖点突变模型。

顶板岩梁支撑系统的分叉集方程，即平衡曲面重叠部分在平面上的投影为：

Δ=4a3+27b2=0

(16)

描述平衡曲面的方程式(16)是一个3次方程，该类方程或有1个实根，或有3个实根，实根的数目和性质可由判别式Δ和a、b是否取零值而定。将平衡曲面x3+ax+b=0绘出，如图10所示。设系统的状态是以x、a、b为坐标的三维空间中的一点为代表，则相点必定位于该曲面上，且总是位于曲面的顶叶或底叶，因为中叶是对应于不稳定状态。即Δ>0时，系统位于上叶，处于稳定状态；Δ=0时，系统位于中叶，处于不稳定状态；Δ<0时，系统位于下叶，处于稳定状态。

图10 尖点突变模型

根据式(14)与式(15)，可知尖点突变模型的控制参量为：

(17)

将控制参量代入式(16)，同时进行简便计算，省略部分恒大于零的相，可知：

(18)

2.3 顶板岩梁突变失稳分析

1)系统受力分析

根据采空区顶板受力情况，将其所受各力计算方式分别如下：

a、岩梁自重对顶板产生的竖向压力q：

q=γh

(19)

式中：γ为顶板岩梁自身容重；h为顶板岩梁自身高度。

b、顶板两侧受水平荷载P[17]：

P=σh

(20)

式中：σ为顶板两侧受水平荷载；h为顶板岩梁自身高度。

研究表明，总体上我国大陆浅层地壳最大水平主应力(σH)与最小水平主应力(σh)随埋深的增大而增大，与埋深存在一定的线性关系，并拟合得到了一定的公式[18]，部分公式如下：

(21)

2)系统失稳的必要条件

由图10可知，系统失稳时必须有a≤0，在此条件下，平衡点有条件跨越分叉集函数，进而引起系统失稳，因此a≤0是系统失稳的必要条件。为保证系统处于稳定状态，则必有a>0。

3)系统失稳的充分条件

由尖点突变理论可知：当系统失稳时，系统状态必须满足分叉集方程，处于临界状态[19]。

对表2进行分析，系数处于稳定状态必须保证分叉集函数不跨过临界点，即Δ>0时。

表2 尖点突变理论状态表

因此，系统失稳的临界条件为Δ=0。

即系统失稳充分条件为Δ<0。

根据式(17)可推知，导数a′>0，因此函数f=a为增函数，故h1

(22)

根据处于断层中间区域采空区的破坏特征，式(22)在实际的工程应用中可用于以下方面：

(1)对于正在作业的采场，可使用式(22)对采空区顶板稳定性进行实时监测。

(2)对未开采的采场，可利用同水平已开采采场监测数据，计算合理顶板厚度。

(3)对于已开采完毕的采场，可使用式(22)判断现有顶板是否稳定，若顶板不稳定可通过加固顶板等措施保障顶板稳定性，保证后续采空区处理时作业的安全性。

3 工程实例

该矿山采空区剖面可简化为图1所示的结构，该矿山由于矿体赋存原因，大部分采空区顶板为矿体，存在部分采空区顶板为中厚层状白云岩。同样由于矿体赋存原因，该矿山采空区并无较统一参数。采空区顶板厚度一致性较好，而且形状较为规整，因此可简化为矩形岩梁结构。

对数值模拟分析，发现两采空区重叠顶底板端部有断层情况下顶板两端中部受压应力比无断层情况下相同位置受压应力减少了0.5 MPa，因此，认为下部产生的垂直向上作用于岩梁与围岩连接处的集中应力F大小为0.5 MPa。将全部参数代入式(22)计算得到最小顶板厚度为5.5 m，取顶板安全系数为2[20]，由此得到顶板安全厚度为11 m。根据采矿设计，该顶板厚度为10 m<11 m，考虑到该矿山采取爆破开采，会对顶板产生损伤，因此认为该顶板处于不稳定状态。

经过对矿山进行的实地调查，发现该采空区顶板已发生部分破坏垮塌。证明理论计算值略大于实际情况，这是由于假设将顶板岩梁视为均匀弹性介质，未考虑岩体内节理裂隙对整体强度的影响。同时对采场上部岩体进行了均一化处理，并未考虑上部存在的少量矿体对地应力的影响。且未考虑爆破等施工过程对顶板的损伤情况。但总体来说，理论计算结果与实际情况吻合较好，计算结果能满足工程中监控顶板稳定性的要求。