Subspace Identification for Closed-Loop Systems With Unknown Deterministic Disturbances
2023-12-22KuanLiHaoLuoSeniorYuchenJiangDejiaTangandHongyanYang
Kuan Li,,, Hao Luo, Senior,, Yuchen Jiang,,,Dejia Tang, and Hongyan Yang,,
Abstract—This paper presents a subspace identification method for closed-loop systems with unknown deterministic disturbances.To deal with the unknown deterministic disturbances, two strategies are implemented to construct the row space that can be used to approximately represent the unknown deterministic disturbances using the trigonometric functions or Bernstein polynomials depending on whether the disturbance frequencies are known.For closed-loop identification, CCF-N4SID is extended to the case with unknown deterministic disturbances using the oblique projection.In addition, a proper Bernstein polynomial order can be determined using the Akaike information criterion (AIC) or the Bayesian information criterion (BIC).Numerical simulation results demonstrate the effectiveness of the proposed identification method for both periodic and aperiodic deterministic disturbances.
I.INTRODUCTION
SYSTEM identification has been widely investigated over the past several decades, which serves as an important tool for monitoring and control purpose [1]–[6].In particular, subspace identification methods (SIMs) can be advantageous over the identification of the state-space model using the process data available, which has been demonstrated to be quite useful for the identification of multivariate systems.Recently,many achievements have been made regarding complex systems and conditions on the subspace identification.In [7],subspace identification for structured state-space models is proposed with the user-defined linear or polynomial parameterization structure.In [8], a unified subspace identification framework for linear parameter-varying (LPV) systems is established in innovation form, which gives an in-depth view on the LPV subspace identification problem.In [9], subspace identification for large-scale interconnected systems with heterogeneous network is investigated with no constrains on the sparse interconnection.
In practice, most industrial processes are required to be operated in practice under closed-loop conditions due to the concern for system safety and product quality.In some cases,the process cannot be separated for open-loop identification tests, for instance, the process needs to be stabilized for bounded outputs or requires online identification.This motivates the subspace identification work for closed-loop systems using the available process data.The main challenge is to deal with the inherited correlation between the control inputs and noise under the feedback control in order to get unbiased estimation results [10].Until now, many various methods have been developed for closed-loop subspace identification, such as innovation estimation method (IEM) [11],predictor-based subspace identification (PBSID) [12], closedloop subspace identification method via principal component analysis (CSIMPCA) [13] and nuclear norm subspace identification method (N2SID) [14].In addition, a novel closed-loop identification method called CCF-N4SID was recently proposed in [15] to integrate the prior knowledge of the controller into the subspace identification framework, based on which the closed-loop identification framework will be used in this work.
On the other hand, practical industrial processes may suffer from various unknown deterministic disturbances, for instance, the flatness of the strip can be greatly influenced due to the roll eccentricities as a typical external unknown disturbance during the rolling process [16] and wind turbines can be prone to unknown periodic disturbances due to the air turbulence [17], [18].These unknown deterministic disturbances can lead to the biased or even totally incorrect identification results if they cannot be well handled.However, less attention has been paid to the in-depth investigation of subspace identification with unknown deterministic disturbances.A subspace identification method with deterministic disturbances is proposed in [19] based on the multiple-input-multiple-output error state-space model identification (MOESP) algorithm and it is derived under the assumption that disturbances can be parametrisable.The base space of the disturbances is not explicitly constructed though it is mentioned that a proper base space can be helpful to the subspace identification under the strong periodic disturbances.A biased-eliminated subspace identification method with constant load or periodic load is proposed in [20], [21] for the consistent estimation where the output responses are decomposed into the disturbed part and the undisturbed part.In addition, the above results have also been extended to the identification of the Hammerstein nonlinear system with periodic or slowly varying disturbances [22], [23].However, few studies have been dedicated to the subspace identification with aperiodic deterministic disturbances.
In this paper, a closed-loop subspace identification method is proposed to deal with the unknown deterministic disturbances under standard feedback control.The influence of unknown deterministic disturbances can be alleviated via the projection onto the constructed row space, which can easily adapt to aperiodic deterministic disturbances with unknown frequencies using the row space constructed by Bernstein polynomials.The main contributions can be summarized as:
1) The row space that can be used to approximately represent the unknown deterministic disturbances is respectively designed using the trigonometric functions and Bernstein polynomials.
2) CCF-N4SID is extended to the closed-loop subspace identification with unknown deterministic disturbances using the oblique projection.
3) A proper Bernstein polynomial order is determined to approximate the unknown deterministic disturbances via the Akaike information criterion (AIC) or Bayesian information criterion (BIC).
The rest of the paper is organized as follows.Section II briefly introduces the preliminaries and formulates the problem.Section III presents the proposed closed-loop subspace identification algorithm with unknown deterministic disturbances.Section IV discusses the choice of the Bernstein polynomial order.Section V verifies the effectiveness of the proposed algorithm via the simulation study.Section VI concludes this work.
II.PRELIMINARIES AND PROBLEM FORMULATION
A. System Description
Consider the following state space modelG(z) with periodic disturbances under the standard feedback control:

Given the controllerK(z) in the form of the state space representation as
wherexc(k)∈Rncdenotes the state vector of the controller,r(k)∈Rmdenotes the reference signal;Ac∈Rnc×nc,Bc∈Rnc×m,Cc∈Rl×ncandDc∈Rl×mare parameter matrices of the controller with appropriate dimensions.
B. Definition and Lemma

Definition 1 and Lemma 1 indicate that the deterministic disturbances in analytic form can be approximated by the Berstein polynomial, which serves as the foundation for the design of the row space that approximately represents the unknown deterministic disturbances in Section III-B.
C. Problem Formulation
In this paper, the identification problem is formulated as determining the matricesA,B,CandDfrom the processG(z)with the unmeasurable deterministic disturbances under the feedback control.The main focus is the solution to two key problems: 1) How to approximate the unknown deterministic disturbances in the subspace context.2) How to identify the process model with unknown deterministic disturbances under closed-loop conditions.
To identify the process model, several assumptions have to be made:
Assumption 1: The standard feedback control loop is wellposed and internally stabilized by the controller.
Assumption 2:G(z) is minimal, i.e., the pair (A,C) is observable and the pair (A,B) is reachable.
Assumption 3: The reference {r(k)} is an ergodic, quasi-stationary random process and can be persistently exciting of any order.
Assumption 4: {w(k)} and {v(k)} are assumed to be zeromean white noise sequences and independent of the reference{r(k)}with covariance matrix
and
where E {·} denotes the expectation operator, σ2wand σ2vdenote the variances of the process noise and measurement noise,respectively;δdenotes the Dirac function.
III.CLOSED-LOOP SUBSPACE IDENTIFICATION WITH UNkNOwN DETERMINISTIC DISTURBANCES
A. Data Equation
Define the stacked vectorsus,kwith lengthsas follows:
By arranging the stacked vectors at different instants, define
whereNis a large integer,ys,kandds,khave the same structure asus,k.
To split the data into past and future horizons, define
wherespandsfdenote the past horizon and the future horizon, respectively.
Iterating on (1), it leads to
where Φfdenotes the noise term, which can refer to [15] for details.Γf,Hu,f, andHd,fare
Consider the predictor model of (1) as follows:
whereKis the Kalman filter gain matrix,AK=A-KC,BK=B-KD,EK=Ed-KFd.

B. Dealing With Unknown Deterministic Disturbances
1)Dealing With Deterministic Disturbances With Known Frequencies: Assume that the deterministic disturbances that can be approximately described by the superposition of finite number of sine functions as follows:
wheredi(k) denotes theith scalar consisting of the disturbance vector,miis the number of distinct frequencies,i=1,2,...,nd.ai,0is the bias ofdi(k).aj, ωjand φjdenote the amplitude, frequency and phase forjth sine components,respectively.
Based on the triangle identity, we have
where βi,j,1=ai,jcos(φi,j), βi,j,2=ai,jsin(φi,j).
According to (22), (21) can be reformulated as
where
Therefore, we have
Note that
it follows that:
Based on (28), it leads to
According to (29),ds,kcan be represented in the compact form as follows:
and
Remark 1: Note thatDb,triis constructed by the trigonometric functions with distinct frequency components.In some cases, the disturbance frequencies can be estimated using the fast fourier transformation (FFT) or other related signal processing techniques.In addition, the calculation of ωi,jkis needed to constructDb,triand it can observed that the frequency estimation error may lead to the deviation ofDb,triespecially whenNis large.Therefore, an empirical suggestion is that the sampling frequencyfshould satisfy≥1.
2)Dealing With Deterministic Disturbances With Unknown Frequencies: In practice, the frequency estimation of the deterministic disturbance can be inaccurate, and it is even impossible to estimate the frequency components of the deterministic disturbance in some cases.In the following, the focus will be on how to approximately describe the row space where the deterministic disturbances belong to when disturbances frequencies are unavailable.
The underlying idea is to approximate the trigonometric function inDb,tribased on the Bernstein polynomial and try to construct the row space that only contains the time sequences,which can be used to address the aperiodic deterministic disturbances as well.

where the entries in therth row andcth column ofQi,jcan be given as
Therefore, we have
Consider the property of the Bernstein basis, i.e.,
and based on (38), it leads to

C. Closed-Loop Subspace Identification
For closed-loop subspace identification, the CCF-N4SID algorithm is extended to the case with unknown deterministic disturbances.
Note that (20) can be rewritten as
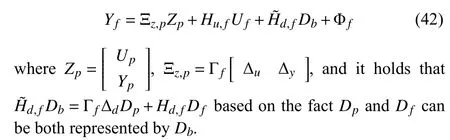
Given the left coprime factorization ofK(z) as
Define the instrumental variableMf[15],
where
The following Theorem 1 gives a feasible solution to the estimation on the extended observability matrix for closedloop systems with unknown deterministic disturbances.
Theorem 1: For a sufficiently largeN, under the assumption

The proposed closed-loop subspace identification method with unknown deterministic disturbances is summarized in Algorithm 1.
IV.DISCUSSION ON THE BERNSTEIN POLYNOMIAL ORDER
Based on the information entropy theory, the Akaike information criterion (AIC) is widely used to deal with the tradeoff between the model complexity and the model fitting goodness.The purpose is to determine a model that can well interpret the data with the least parameters.Therefore, the following AIC indicators can be helpful to determine the proper order of the Bernstein polynomial:

Algorithm 1 Closed-loop subspace identification with unknown deterministic disturbances Input: ,.Output: A, B, C and D.sp sf UpUfYp Yf u(k)y(k)S1: Set , and N, construct Hankel matrices , and according to (12).S2: Construct the row space that approximates the unknown deterministic disturbances as follows,Db a) When frequencies of deterministic disturbances are known, construct as ,Db,tri Db b) When frequencies of deterministic disturbances are unknown,construct as.K(z) ˆVc(z)ˆUc(z)Db,bern Db S3: Do left coprime factorization on , obtain and ,construct and according to (45) and (46).Mf =Kc Kcv,f Kcu,f v,f Uf +Kcu,f Yf S4: Construct the instrumental variable.Γf ˘Xk,N Hu,f S5: Do LQ factorization as (47), obtain and.S6: Identify the matrices A, B, C and D.
Therefore, an appropriate order of the Bernstein polynomial should satisfy
Note that the penalty coefficient of model parameter numbers is set to be 2 for AIC.To avoid the overfitting, the penalty coefficient of model parameter numbers can be properly increased.As a special case, when the penalty coefficient is set to beln(N), it leads to the Bayesian information criterion (BIC), i.e.,
In terms of performance indicators, it is suggested that AIC and BIC can be both analyzed for performance evaluation to determine a proper Bernstein polynomial order in most cases.
V.SIMULATION STUDY
Consider a linear invariant systemG(z), the parameter matrices are given as
The controllerK(z) can be designed arbitrarily such that the system is stabilized.
During the simulation, the noise powers of two reference signals are set to bePn=0.2 andPn=0.3, respectively.The noise powers ofw(k) andv(k) are both set to bePn=0.0002.The sampling time is set to bets=0.002 s.The parameter settings areN=5000,sp=30 andsf=8, respectively.
Assume that there exists a deterministic disturbance in the closed-loop system with five distinct frequencies as follows:
where the amplitudea1,jand the frequency ω1,jcan be referred to Table I for simulation settings.

TABLE I PARAMETERS OF DETERMINISTIC DISTURBANCE
To verify the effectiveness of the proposed algorithm for closed-loop identification with unknown deterministic disturbances, Fig.1 compares the method in [15] while ignoring the deterministic disturbance (i.e., CCF-N4SID), the proposed algorithm usingDb,tri(i.e., CCF-N4SID-D1) and the proposed algorithm usingDb,bern(i.e., CCF-N4SID-D2) withnb=8 andnb=9.
From Fig.1, it can be observed that CCF-N4SID delivers the wrong pole estimation results due to the fact that it is directly implemented while ignoring the influence of the unknown deterministic disturbances, which implies that the dynamics of the identified model cannot be consistent with the real one.In contrast, the proposed algorithm usingDb,triorDb,berncan both obtain a relatively reliable pole estimation.It should be mentioned that the pole estimation results are less accurate with obviously biased estimation for poles located on the left half of the unit circle whennb=8.However, the pole estimation performance improves a lot whennb=9, which is competitive to the pole estimation results via the proposed algorithm usingDb,tri.Note that the discussion above in fact indicates the importance of the proper choice of the Bernstein polynomial order.
To determine the proper Bernstein polynomial order, AIC and BIC are respectively tested as shown in Fig.2, from which it can be observed that the AIC curve and BIC curve both reach the minimum whennb=9 with the range for the integernb∈[1,12].In addition, the two curves begin to climb up with the increase ofnbdue to the possible overfitting and the BIC curve shows more obvious increasing trend whennb>9due to the larger penalty coefficient of model parameter numbers.The above analysis implies thatnb=9 can be indeed a proper choice for the construction ofDb,bern.
In addition, Fig.3 compares the estimation error of Markov parametersCAiBunder different Bernstein polynomial ordersnb.The evaluation indicator for the estimation error ofCAiBis
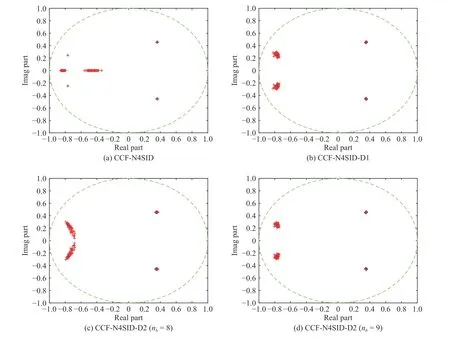
Fig.1.Comparison of pole estimation with deterministic disturbance ( sp=30, sf =8).

Fig.2.The determination of the Bernstein polynomial order.
given as follows:
where //·//Fdenotes the Frobenius norm.Note that the logarithm function is used to magnify the estimation error for better visualization.
From Fig.3, it can be observed that the estimation error ofCAiBgradually decreases with the increase ofnbuntil it reaches the minimum whennb=9.Note that the estimation error shows a slight increase whennb=10 compared with the result whennb=9, which again verifies the reasonability of the choice of the Bernstein polynomial order using AIC or BIC.
Fig.4 shows the structure of the identifiedHu,fwhennb=9.In Fig.4, the light color means that the entries in the identifiedHu,fare close to 0.Therefore, it can be observed that the identifiedHu,fholds the lower triangular Topelitz structure well though no extra structural constraints are applied, which verifies the effectiveness of the proposed algorithm.
Table II shows the comparison of identification performance in case of different disturbance types including constant, signal in (56), ramp and chirp signals, which involves the periodic and aperiodic signals during the test.The disturbance types in the above four cases are described as
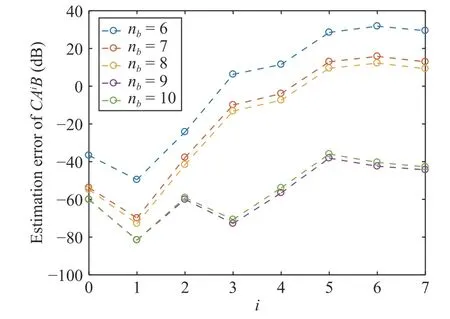
Fig.3.Comparison of the estimation error ofCAiB under different n b.

Fig.4.The structural properties of the identified H u,f (n b=9).
Case 1(Periodic): The deterministic disturbance is a constant signal with
Case 2(Periodic): The deterministic disturbance is the superposition of five distinct frequencies as in (56), i.e.,
Case 3(Aperiodic): The deterministic disturbance is a ramp signal with the slope 0.2/s, i.e.,
Case 4(Aperiodic): The deterministic disturbance is a chirp signal varying from 0.1 Hz to 20 Hz in 100 s with amplitude 1, i.e.,
wheref(kts)=0.1+0.199kts.
To quantify the accuracy of estimated poles, the indicatorErrpole,iis defined as the error between the true poles and the average of estimated poles,
where λiand λidenote theith true pole and the average ofith estimated poles, respectively.

In addition, the determined Bernstein polynomial order via AIC and BIC is shown in Table II.It should be noted that the constant signal can be described by a row vector with all elements being 1, i.e., the polynomial order is zero, and the ramp signal is linear that can be described by the first-order polynomial.
From Table II, it can be observed that CCF-N4SID delivers the wrong estimation of the poles and Markov parameterE7with quite large errors for all four disturbance types.However,CCF-N4SID-1 and CCF-N4SID-2 can deliver the correct identification performance with a small estimation error of the poles andE7, which demonstrates the effectiveness of the proposed identification methods for both periodic and aperiodic deterministic disturbances.
VI.CONCLUSION
In this paper, a subspace identification method is proposed for closed-loop systems with unknown deterministic disturbances in order to improve the estimation performance.To overcome the influence of the unknown deterministic disturbances, the row space that can be used to approximately represent the unknown deterministic disturbances is constructed using the trigonometric functions or Bernstein polynomials depending on whether the disturbance frequencies are known,which can be used to address the aperiodic deterministic disturbances.CCF-N4SID is then extended to the subspace identification with unknown deterministic disturbances using the oblique projection under feedback control.Moreover, the Bernstein polynomial order can be properly determined using AIC or BIC.The numerical example demonstrates that the proposed method can effectively alleviate the influence of the deterministic disturbances with reliable identification results.
The LQ factorization in (47) can be interpreted by decomposingYfinto the following four parts [25]:
APPENDIx PROOF OF THEOREM 1

TABLE IICOMPARISON OF IDENTIFICATION PERFORMANCE IN CASE OF DIFFERENT DISTURBANCE TYPES
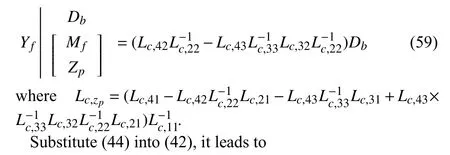
where
In addition, (60) can be rewritten as
Recall that
Comparing (62) with (63), we have
Substituting (64) into (61), it leads to
Therefore, whensp→∞, we have
and
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- A Game Theoretic Approach for a Minimal Secure Dominating Set
- Knowledge Transfer Learning via Dual Density Sampling for Resource-Limited Domain Adaptation
- Magnetic Field-Based Reward Shaping for Goal-Conditioned Reinforcement Learning
- Multi-Blockchain Based Data Trading Markets With Novel Pricing Mechanisms
- GenAI4Sustainability: GPT and Its Potentials For Achieving UN’s Sustainable Development Goals
- Resilient Event-Triggered Control of Connected Automated Vehicles Under Cyber Attacks
