地面基准站网与星载GNSS融合的高中低轨卫星联合精密定轨
2023-12-22金炜桐张京奎武子谦
金炜桐,张京奎,武子谦
地面基准站网与星载GNSS融合的高中低轨卫星联合精密定轨
金炜桐,张京奎,武子谦
(中国电子科技集团公司第五十四研究所,石家庄 050081)
下一代导航系统拟纳入低轨卫星(LEO)作为增强和备份。研究了地面基准站网与星载GNSS融合的高中低轨卫星联合精密定轨(POD)理论与方法,基于实测国际地面站(IGS)和低轨卫星星载GNSS数据,通过建立高精度动力学模型和观测模型,根据全球测站和区域测站两种情况进行了导航星与低轨星的联合精密定轨试验。结果表明,联合定轨可同时获得导航星和低轨星厘米级的定轨精度。低轨星作为高动态天基测站,对导航星定轨精度的提升程度可达20%~90%。
联合精密定轨;低轨卫星;导航卫星;天基测站
0 引言
低轨卫星作为高精度对地观测的天基平台,已在地球重力场反演、卫星移动通信、海洋大气监测等众多科学和工程领域得到广泛应用[1]。相比于高中轨导航卫星,低轨卫星距地表更近,运行速度更快,落地信号功率更强;相比于地面测站,低轨卫星相当于高动态天基测站,在可视GNSS卫星数量、全球天基监测覆盖性等方面具有天然优势,能够全面提升卫星导航定位服务的精度、完好性、可用性和抗干扰能力[2]。结合低轨星座,进行高中低轨联合快速高精度定位已成为下一代智能位置服务的发展方向。
快速高精度定位依赖于高精度时空基准的建立和维持。利用地面基准网和低轨卫星观测的GNSS数据进行高中低轨卫星联合精密定轨(以下简称联合精密定轨)是确立高精度时空基准的必然发展趋势。算法方面,联合精密定轨包括“两步法”和“一步法”两种,两者的区别在于前者先基于地面站网确定导航星的轨道和钟差,再将导航星轨道视为已知值,利用低轨卫星星载GNSS数据对低轨卫星精密定轨;后者则是结合地面站网和星载GNSS数据联合处理同时得到导航星和低轨卫星的轨道和钟差。有研究表明,“一步法”在定轨精度方面略优于“两步法”[3]。数据方面,Zhu S等人首次基于全球分布的40个测站以及3颗低轨卫星的GNSS数据进行了联合精密定轨,GPS轨道和低轨卫星轨道确定精度分别提高了47%和22%[4]。随后众多国内外学者基于实测或仿真数据,对联合精密定轨开展了相关研究,并获得了较好的精度提升效果[5-8]。
本文阐述了“一步法”高中低轨卫星联合精密定轨基本理论及详细算法流程,并基于实测地面站网数据和5颗低轨卫星星载GNSS数据开展联合精密定轨试验,详细介绍了试验中的模型配置和解算策略,并对定轨结果进行详细分析,为未来的高中低轨联合精密定位服务提供参考。
1 高中低轨卫星联合精密定轨理论与算法流程
卫星精密定轨本质上是对卫星轨道的测量数据进行高精度建模,将卫星初始历元轨道等视为待估模型参数,通过调整此类参数使模型能够在某种准则下最佳拟合测量数据的过程[9]。
联合精密定轨使用的测量数据为地面基准站网和星载接收机观测的GNSS数据,通常对其建立伪距和载波相位的非差双频无电离层组合测量模型,具有如式(1)所示形式

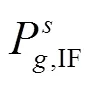
对式(1)进行线性化,可有

对于联合精密定轨,其待估模型参数可表示为

联合精密定轨算法采用加权最小二乘原理,通过观测量预处理、轨道积分、理论观测量和残差计算进行迭代处理,得到收敛解,最后进行模糊度固定得到最终联合精密定轨结果,具体流程如图1所示。

图1 联合精密定轨算法流程
特别地,引入低轨卫星作为“天基测站”对导航星定轨具有增强作用。传统的导航星精密定轨方法仅依赖于地面基准站,而低轨卫星运行速度快且具有一定的轨道高度,截止高度角较小。另外,如式(1)和式(2)所示,在对低轨星的星载GNSS数据进行建模时可忽略对流层影响,也是提升导航星定轨精度的重要原因之一。
2 高中低轨卫星联合精密定轨试验
2.1 观测数据及模型配置
本文选取了2022年年积日为211~214天全球85个国际地面站(International Ground Station,IGS)观测数据与SWARM-A/B/C[10]、GRACE-C/D[11]共5颗低轨卫星的星载GPS数据。其中85个IGS地面站构成全球基准站网,分布如图2所示;5颗低轨卫星的轨道高度、轨道倾角等信息如表1所示。
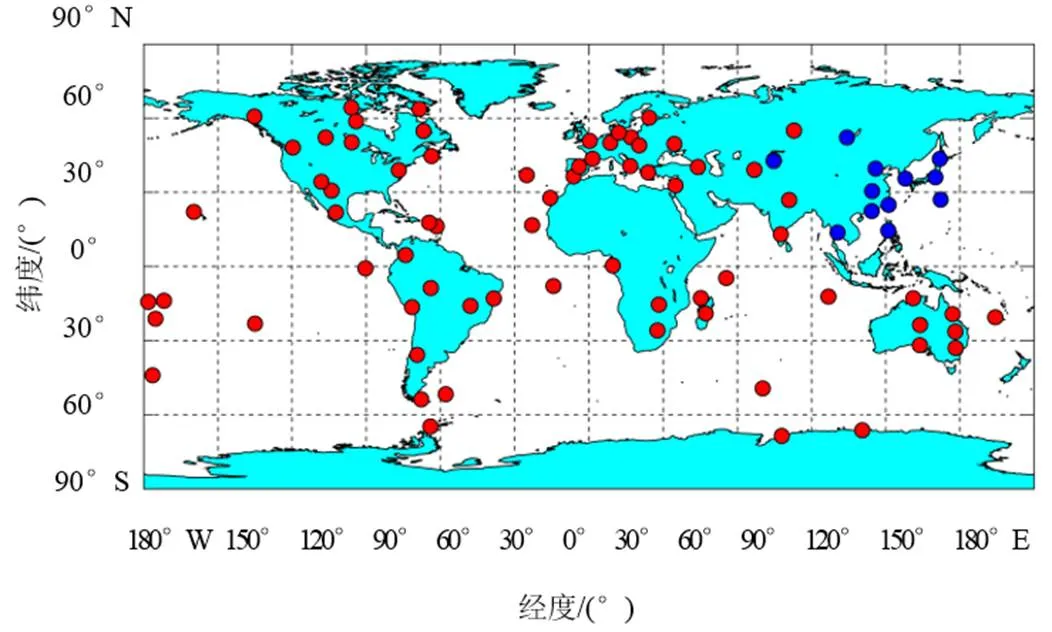
图2 所选全球IGS测站分布图
本节设计两种联合精密定轨试验方案,如表2所示。第一种方案进行全球测站联合定轨,即采取全部85个地面测站和5颗低轨卫星的数据进行联合精密定轨;第二种方案进行区域测站联合定轨,即采用其中12个分布在亚太地区的测站(本文称区域测站,图2中用蓝色标明)和5颗低轨卫星数据进行联合精密定轨,旨在进一步凸显有限测站情况下联合精密定轨的优势。对于每种方案,还设计了仅基于地面测站的导航星精密定轨对比试验,旨在突出在全球测站和区域测站情况下加入低轨星数据对导航星精密定轨的增强作用。联合精密定轨试验采用的模型如表3所示。

表1 5颗低轨卫星信息
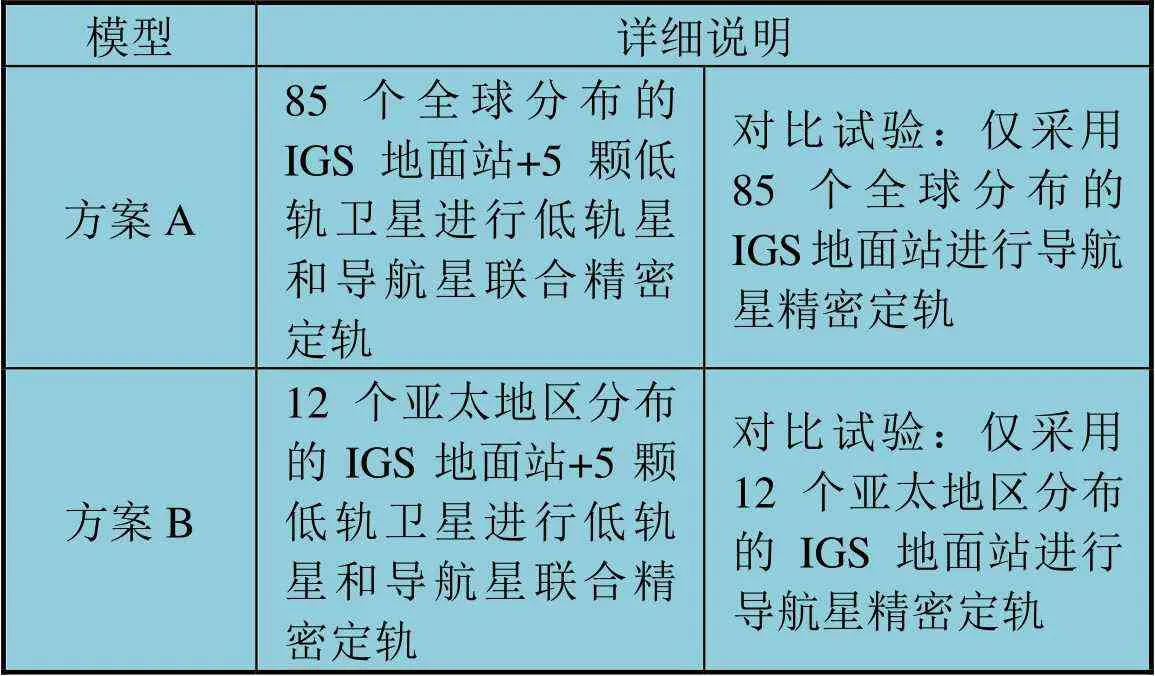
表2 联合精密定轨试验方案

表3 联合精密定轨试验模型配置
2.2 全球测站的高中低轨卫星联合精密定轨
本节采用欧洲定轨中心CODE发布的导航星精密轨道产品与ESA发布的SWARM精密轨道产品、JPL发布的GRACE-FO精密轨道产品作为参考,将联合精密定轨的结果与之作差,进行定轨精度统计分析。
基于85个全球分布的IGS站地面观测数据和5颗低轨卫星星载数据联合解算(方案A)的导航星和低轨星定轨结果如图3和图4所示。两图横轴分别表示GPS卫星PRN号和低轨星短名(如表1所示),两图纵轴分别表示2022年年积日 211~214天(4个弧段)的GPS卫星轨道均方根(Root Mean Square,RMS)误差的平均值和低轨星轨道RMS平均值。可以看出,GPS卫星轨道RMS最大约6 cm,平均值为3.1 cm;5颗低轨星轨道RMS最大约1.5 cm,平均值为1.2 cm,达到了联合精密定轨的厘米级精度水平。
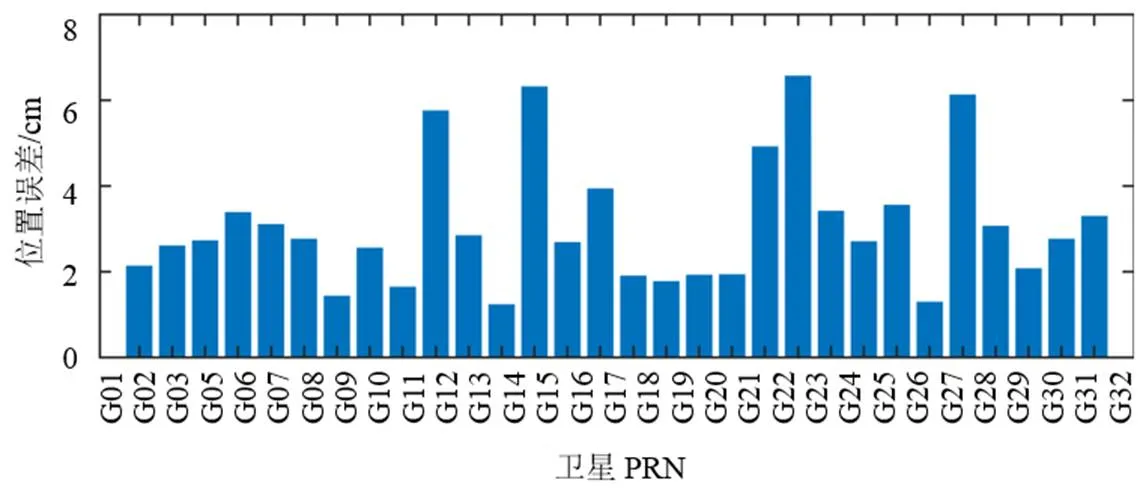
图3 全球测站联合精密定轨试验导航星定轨结果

图4 全球测站联合精密定轨试验低轨星定轨结果
2.3 区域测站的高中低轨卫星联合精密定轨
本节采用与2.2节相同的方式评估区域测站联合精密定轨精度。
基于12个亚太地区分布的IGS站地面观测数据和5颗低轨卫星星载数据联合解算(方案B)的导航星和低轨星定轨结果如图5和图6所示。两图横轴分别表示GPS卫星PRN号和低轨星短名(如表1所示),两图纵轴分别表示2022年年积日211~214天(4个弧段)的GPS卫星轨道RMS的平均值和低轨星轨道RMS平均值。GPS卫星轨道RMS最大约9.6 cm,平均值为7.1 cm;5颗低轨星轨道RMS最大约3.2 cm,平均值为3.1 cm。相比于85个全球地面测站与5颗低轨星的联合定轨,区域测站由于覆盖性不如全球测站,因此联合定轨试验中导航星和低轨星的定轨精度均低于全球测站,但也达到了厘米级精度水平。

图5 区域测站联合精密定轨试验导航星定轨结果

图6 区域测站联合精密定轨试验低轨星定轨结果
2.4 对比试验定轨结果及理论分析
为突出低轨星星载观测数据对地面测站导航星精密定轨的增强作用,分别仅采用85个IGS地面站和12个区域测站(方案A和方案B的对比试验)对导航星进行精密定轨,对比结果如表4所示。

表4 联合精密定轨对比试验结果
表4中85地面站和85地面站+5颗低轨卫星对应于表2中的方案A,12地面站和12地面站+5颗低轨卫星对应于表2中的方案B,RMS表示GPS卫星轨道RMS的平均值。对于全球85个测站均匀分布的情况,由于地面测站数量多且在全球分布均匀,GPS卫星定轨精度已经可达到4 cm左右,引入低轨星后精度提升了1 cm,提升程度约为20.5%,具有轻微增强作用;而区域测站的情况下,引入低轨卫星的优势巨大,由于亚太地区分布的测站无法覆盖全球,仅12个区域测站的导航星精密定轨精度较差,此时低轨星作为高动态天基测站的优势体现地较为明显,对导航星轨道的增强程度提升了约90%。特别地,即使在区域测站+5颗低轨卫星的情况下,导航星定轨精度仍然低于仅利用全球分布地面站的情况。实际上,由于这5颗低轨卫星轨道高度、倾角等轨道参数类似,引入更多不同类型的低轨卫星可进一步提升定轨精度。
3 结语
本文介绍了高中低轨卫星联合精密定轨基本理论和详细算法流程,并基于实测星载GNSS数据和地面站网数据,开展了联合精密定轨试验分析。结果表明,联合定轨可获得导航星和低轨星厘米级的定轨精度。当地面测站数量较多且全球分布时,低轨星对导航星轨道的增强不明显,约为20%;在测站数量较少且区域分布的情况下,低轨星作为高动态天基测站的优势体现的较为明显,对导航星定轨精度的提升程度可达90%。
[1] 张柯柯. 低轨卫星精密定轨及其与GNSS导航卫星联合轨道确定[D]. 武汉:武汉大学,2019.
[2] 马福建. 低轨导航增强星座优化与信号频率设计研究[D]. 武汉:武汉大学,2021.
[3] 匡翠林. 利用GPS非差数据精密确定低轨卫星轨道的理论及方法研究[D]. 武汉:武汉大学,2008.
[4] Zhu S,Reigber C,König R. Integrated adjustment of CHAMP,GRACE,and GPS data[J]. Journal of Geodesy,2004,78(1):103-108.
[5] Li X,Zhang K,Ma F,et al. Integrated precise orbit determination of multi-GNSS and large LEO constellations[J]. Remote Sensing,2019,11(21):2514.
[6] Hugentobler U,Jäggi A,Schaer S,et al. Combined processing of GPS data from ground station and LEO receivers in a global solution[M]. A Window on the Future of Geodesy. Springer,Berlin,Heidelberg,2005:169-174.
[7] 曾添. 低轨卫星增强导航星定轨试验及数据处理方法研究[D]. 郑州:信息工程大学,2017.
[8] 张伟. 低轨卫星增强GNSS定轨及其对地球自转参数的贡献[D]. 武汉:武汉大学,2021.
[9] 李济生. 人造卫星精密轨道确定[M]. 北京:解放军出版社,1995.
[10] Friis-Christensen E,Lühr H,Knudsen D,et al. Swarm–an Earth observation mission investigating geospace[J]. Advances in Space Research,2008,41(1):210-216.
[11] Kornfeld R P,Arnold B W,Gross M A,et al. GRACE-FO:the gravity recovery and climate experiment follow-on mission[J]. Journal of spacecraft and rockets,2019,56(3):931-951.
[12] Förste C,Bruinsma S,Rudenko S,et al. EIGEN-6S4:A time-variable satellite-only gravity field model to d/o 300 based on LAGEOS,GRACE and GOCE data from the collaboration of GFZ Potsdam and GRGS Toulouse[J]. Disp. em:http://doi. org/10.5880/icgem,2016.
[13] Standish E M. JPL planetary and lunar ephemerides,DE405/LE405,IOM 312[Z]. Jet Propulsion Laboratory publication F-98-048,Pasadena/CA,1998.
[14] Petit G,Luzum B. IERS conventions (IERS Technical Note No.36)[Z]. Bureau International Des Poids et Mesures Severs,France,2010.
[15] Lyard F,Lefevre F,Letellier T,et al. Modelling the global ocean tides:modern insights from FES2004[J]. Ocean dynamics,2006,56(5):394-415.
[16] Arnold D,Meindl M,Beutler G,et al. CODE’s new solar radiation pressure model for GNSS orbit determination[J]. Journal of geodesy,2015,89(8):775-791.
[17] Wen H.Y.,Kruizinga G.,Paik M.,et al. Gravity Recovery and Climate Experiment Follow-On (GRACE-FO) Level-1 Data Product User Handbook[Z]. Technical Report,GRACE Technical Report,JPL D-56935 (URS270772),USA,2019.
[18] Montenbruck O,Hackel S,van den Ijssel J,et al. Reduced dynamic and kinematic precise orbit determination for the Swarm mission from 4 years of GPS tracking[J]. GPS solutions,2018,22(3):1-11.
[19] Picone J M,Hedin A E,Drob D P,et al. NRLMSISE‐00 empirical model of the atmosphere: Statistical comparisons and scientific issues[J]. Journal of Geophysical Research:Space Physics,2002,107(A12):SIA 15-1-SIA 15-16.
[20] Böhm J,Niell A,Tregoning P,et al. Global Mapping Function (GMF):A new empirical mapping function based on numerical weather model data[J]. Geophysical Research Letters,2006,33(7).
[21] Saastamoinen J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites[J]. The use of artificial satellites for geodesy,1972:247-251.
Integrated Precise Orbit Determination of High, Medium and Low Earth Satellites Using Ground Station Network and Spaceborne GNSS Receiver Data
JIN Weitong, ZHANG Jingkui, WU Ziqian
The next-generation navigation system is proposed to incorporate Low Earth Orbit (LEO) satellites as an enhancement and backup. The theory and method of integrated Precise Orbit Determination (POD) of high, medium and low orbit satellites using ground station network and spaceborne GNSS receiver data is studied. A high-precision dynamic model and observation model are established, and the integrated POD experiments of navigation satellites and LEO satellites are carried out under the cases of global station and regional stations using real data. The results show that the integrated POD can obtain centimeter-level POD accuracy for both navigation satellites and LEO satellites simultaneously. As a high-dynamic space-based station, the LEO satellites can help improve the POD accuracy of navigation satellites by 20%~90%.
Integrated Precise Orbit Determination; Low Earth Orbit Satellites; Navigation Satellites; Space-Based Station
P228
A
1674-7976-(2023)-06-395-06
2023-06-28。
金炜桐(1992.12—),黑龙江齐齐哈尔人,博士,工程师,主要研究方向为卫星精密定轨理论。
