基于空间平滑多重信号分类算法的低角目标探测

李宏亮，张大智，朱传明，曹广地

基于空间平滑多重信号分类算法的低角目标探测

李宏亮，张大智，朱传明，曹广地

（中国电子科技集团公司第二十研究所，西安 710068）

基于阵列信号处理的目标回波到达方向（DOA）估计算法具有分辨力强、估计精度高、抗干扰能力强的特点，是目标测向的研究热点。多重信号分类（MUSIC）算法就是基于阵列信号处理的目标测向算法之一，传统的多重信号分类算法假设目标回波是互不相关的，这导致其应用效果受到较大的限制。在传统多重信号分类算法的基础上，采用空间平滑多重信号分类算法进行目标回波解相干处理，推导给出了估计目标回波到达角度的表达式以及该算法的实现流程框图，并结合数值模拟结果以及实际应用场景对该算法的优缺点进行了对比分析。空间平滑多重信号分类算法在低角目标探测、单目标多径问题、多目标到达角度与多目标数量估计等方面具有一定优势。

回波到达方向；相干回波；多重信号分类

0 引言

在目标探测、跟踪的过程中需要解决的一个基本问题是如何确定目标信号入射角度，即如何确定目标波达方向（Directing of Arrival，DOA）。DOA估计是阵列信号处理中重要研究方向，特别是多目标DOA估计、相干回波DOA估计和复杂电磁环境下DOA估计等更是当下研究热点。DOA估计在雷达、通信和声呐等国防军事领域有广阔的应用前景。

DOA估计就是利用处于空间中不同位置的天线阵列，接收目标回波，由于处于不同位置阵元对同一回波信号接收存在相位差，从而会形成谐波，通过对谐波进行处理进而求得目标DOA。目前DOA估计理论中，较为经典的一种估计方法是Schmidt提出的基于矩阵特征值分解的多重信号分类（Multiple Signal Classification，MUSIC）算法[1]，该方法通过对接收信号数据矩阵进行特征值分解，将数据矩阵转化为由信号向量和噪声向量构成的正交子空间，进而根据这个特性求得波达方向[2-3]。

由于多路径传播的特点，对于低角度目标的探测、跟踪一直是重点、难点，尤其随着当下低慢小目标和快速掠海目标的快速发展，越来越多的目标都具备低角飞行的特点。MUSIC算法对于多目标到达角度估计、多目标数量估计以及单目标多径问题的处理与单目标到达角的估计具有较大的理论优势[6]。传统的MUSIC算法要求入射到接收阵列的目标回波具有不相关特性，但实际情况中不同目标回波或同一目标的多径回波往往具有较强的相关性，导致该算法在使用过程中具有较大限制。本文在传统MUSIC算法基础上，采用空间平滑MUSIC算法进行解相干处理，通过波峰搜索进而获取DOA[4-5]。

1 MUSIC算法

1.1 MUSIC算法推导

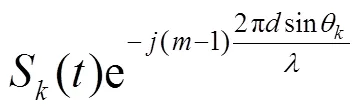
第个阵元处信号总输出可以表示为

为方便表述与后续推导，将式（2）用矩阵形式表示为[3]

式中：

对阵列输出信号进行相关处理，得到阵列输出信号的协方差矩阵为

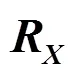
将式（5）和式（6）联立，可得：

即

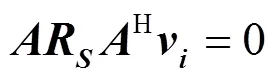
进一步推导可以得出

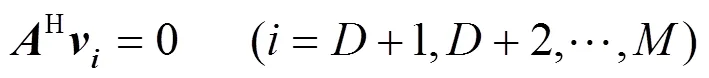
根据式（9），即可利用噪声特征向量求解目标信号方向。以各噪声特征向量为矩阵的列数据，构造噪声矩阵为

则

在实现过程中，由于噪声的干扰，往往寻求极小值难度较大且准确率低，所以将式（12）再次转化为

1.2 空间平滑MUSIC算法

空间平滑MUSIC算法通过对接收数据进行预处理，将接收阵列分成若干子阵，分别对各子阵的信号相关矩阵进行特征值分解从而实现目标相关信号的解相关处理，进而能够处理多目标回波、多路径回波等复合性问题[8-9]。

空间平滑MUSIC算法实现过程[3-5]如下：假设共个阵元，分成个子阵，每个子阵阵元数为，如图1所示。

图1 空间平滑多重信号分类算法示意图

取左侧第1个子阵为参考子阵，则第个子阵数据模型为

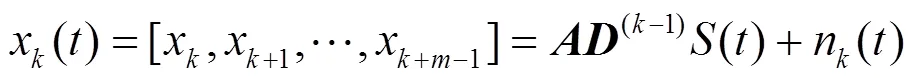
式中，

故第个子阵数据协方差矩阵为

空间平滑的数据协方差矩阵为

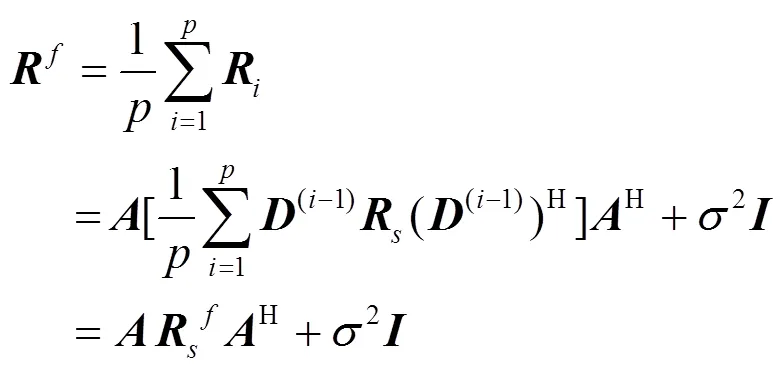
1.3 空间平滑MUSIC算法流程

根据上述推导，给出空间平滑MUSIC算法如图2所示。

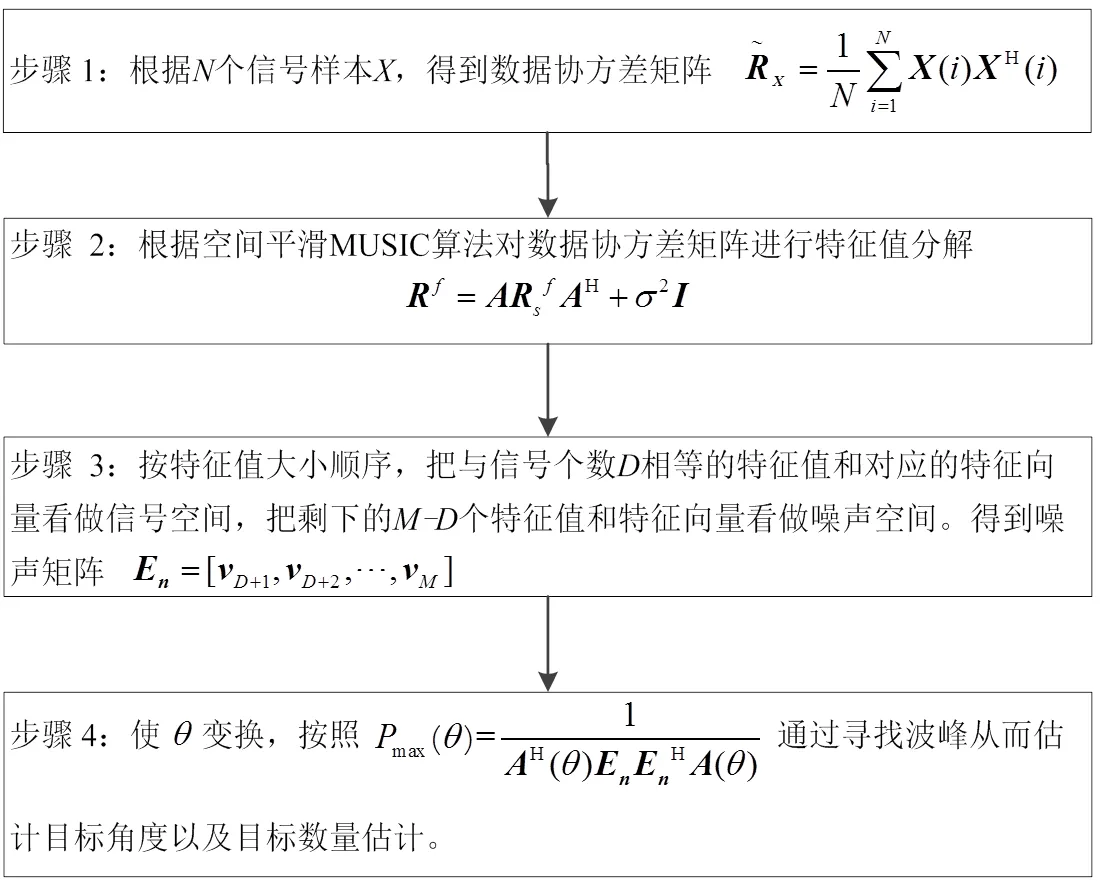
图2 空间平滑MUSIC算法框图

2 数值模拟

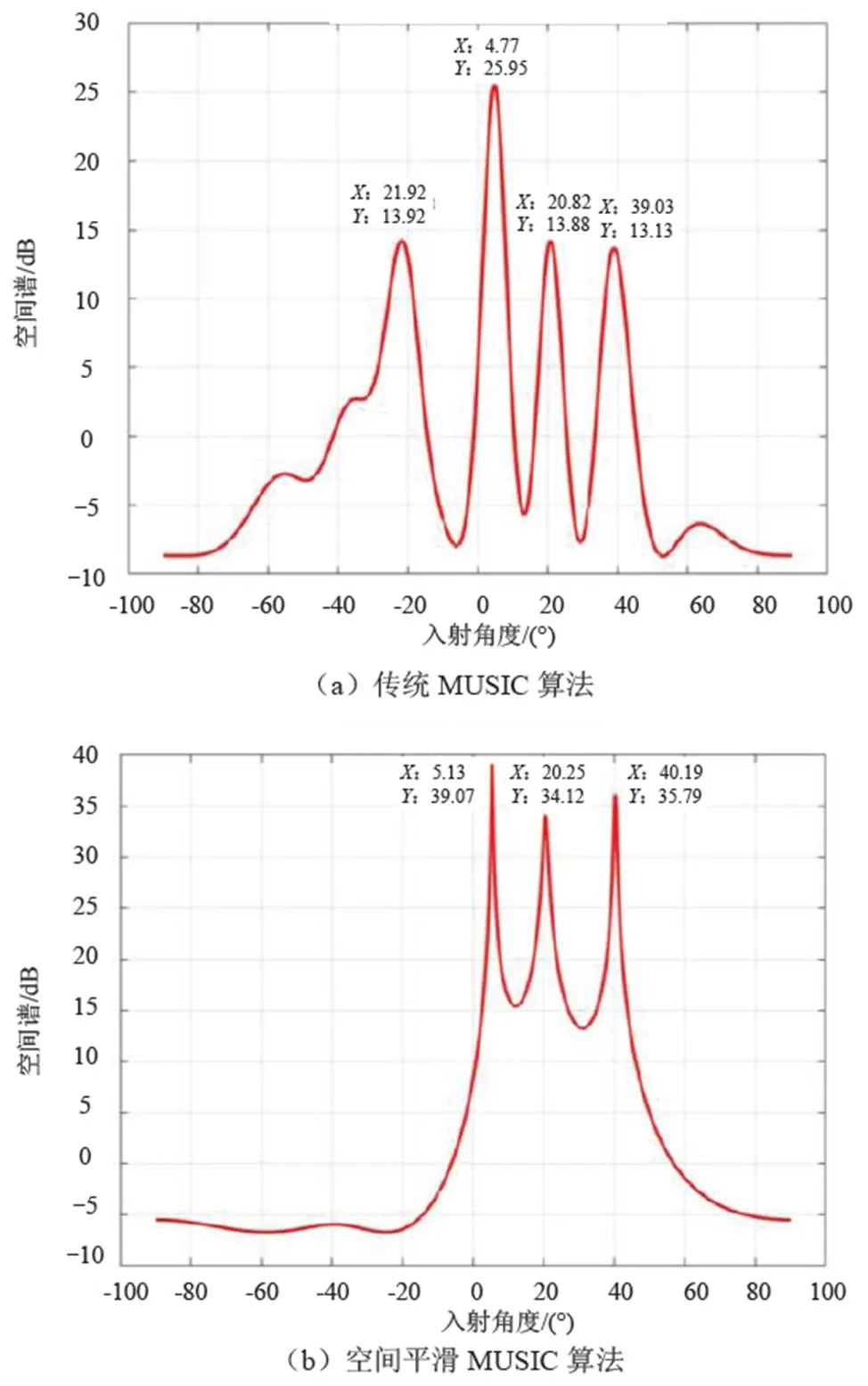
图3 数值模拟结果

从数值模拟结果不难看出，当目标回波为相关信号时，传统MUSIC算法适用性受到限制，如图3（a）所示，将三个目标回波信号识别为四个目标。而空间平滑MUSIC算法可以对目标信号解相关处理，从而能够准确估计目标DOA，如图3（b）所示。此外，通过数值模拟结果可以看出，对于低角目标，该算法能够较为准确的估计DOA，这也为低角目标探测提供了思路和参考。

3 算法优缺点分析

空间平滑MUSIC算法的主要优势有：

1）能够对不同目标回波进行到达角度估计，有助于进行目标数量估计，如图4（a）所示。

2）单一目标多路径传播情况下，目标回波具有强相关特性，空间平滑MUSIC算法能够在此种场景下进行解相关处理，有助于进行单一目标多径问题的处理，如图4（b）所示。

3）对低角到达目标，如单一目标或基于不相干前提下的多目标，能够进行较为精确的到达角度估计与目标探测。

当然，由于空间平滑MUSIC算法的多种假设前提，导致该算法也存在一定的限制：

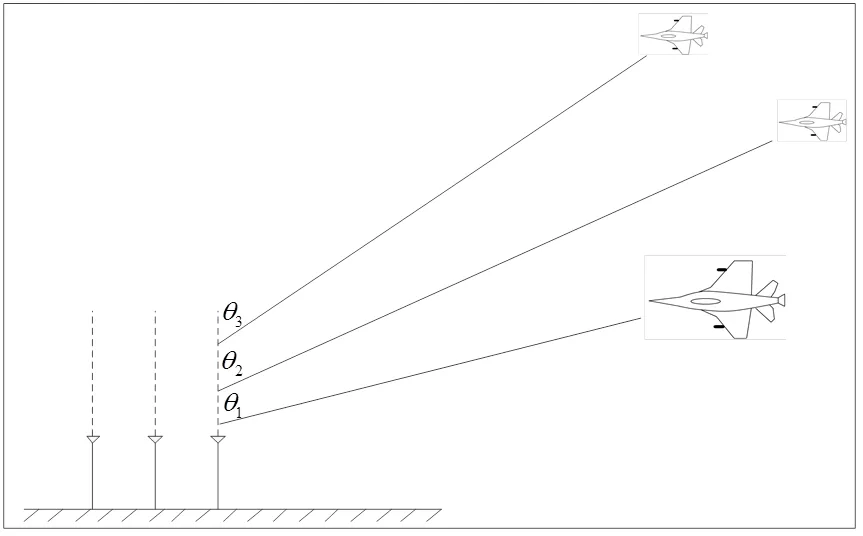
1）低角多目标到达时，由于多路径传播的特点，导致该算法对于目标数量和到达角度的估计存在一对多的情况，无法准确定位某一特定目标的到达角度，存在角度估计错误的风险，如图4（c）场景三所示。

2）由于空间平滑算法将接收阵列分成了多个子阵，减小了阵元数和阵列孔径，导致可估计的目标数目变少，而且在目标非相关情况下，空间平滑算法的分辨力较之传统MUSIC算法有所下降。

（a）场景一

（b）场景二

（c）场景三

4 结语

本文基于空间平滑MUSIC算法，推导给出了通过峰值搜索，估计目标回波到达角度的表达式及该算法的实现流程，并结合数值模拟结果以及实际应用场景，对该算法的优缺点进行了对比分析。基于空间平滑MUSIC算法可以实现对相干目标回波的处理，有助于对多目标到达角度的估计、多目标数量的估计以及单目标多径问题的处理与单目标到达角的估计，进而有助于进行低角目标的探测和跟踪。

[1] R. O. Schmidt. Multiple emitter location and signal parameter specetral estimation[J]. in Proc.RADCS pectrum Estimation Workshop，1979.10，or IEEE Trans，1986.3，AP-34（3）：276-280.

[2] 张贤达. 现代信号处理[M]. 北京：清华大学出版社，2002.

[3] 王永良，陈辉，彭应宁，等. 空间谱估计理论与算法[M]. 北京：清华大学出版社，2004.

[4] 郑洪. MUSIC算法与波达方向估计研究[D]. 成都：四川大学，2005.

[5] 林吉平. 阵列信号波达方向估计算法研究[D]. 西安电子科技大学，2014.

[6] 张洲. 无源测向关键技术及算法实现[D]. 成都：电子科技大学，2019.

[7] 宋德枢，梁国龙，王燕. 机动目标DOA跟踪粒子滤波算法[J]. 信号处理，2014（7）：861-866.

[8] 张秦，张林让，师俊朋，等. 基于空间差分重构的MIMO雷达低空目标DOA估计方法[J]. 西北工业大学学报，2018（5）：465-470.

[9] 刘源. 米波阵列雷达低仰角目标测高方法研究[D]. 西安：西安电子科技大学，2019.

[10] 王洪帧，郑桂妹，宋玉伟. 基于稀疏阵列的米波TR MIMO雷达低空目标测高方法[J]. 信号处理，2023（2）：310-322.

Low Angle Target Detection Based on Spatial Smoothing MUSIC Algorithm

LI Hongliang, ZHANG Dazhi, ZHU Chuanming, CAO Guangdi

The target echo Directing of Arrival (DOA) estimation algorithm based on array signal processing has the characteristics of strong resolution, high estimation accuracy and strong anti-interference ability. These algorithms are also research hotspots in target direction finding. The Multiple Signal Classification (MUSIC) algorithm is one of the DOA estimation algorithms, and the traditional MUSIC algorithm assumes that the target echoes are not correlated with each other, which leads to its application effect being greatly limited. Based on the traditional MUSIC algorithm, the spatial smoothing MUSIC algorithm is used to decoherence the target echo, and the expression for estimating the target DOA and the implementation flow block diagram of the algorithm are derived. The advantages and disadvantages of the algorithm are compared and analyzed based on the numerical simulation results. The MUSIC algorithm has certain advantages in low-DOA, single target multipath problem, multi-target DOA and targets number estimation.

Directing of Arrival; Coherent Echo; Multiple Signal Classification

TN957

A

1674-7976-(2023)-06-461-05

2023-05-18。

李宏亮（1993.02—），陕西西安人，硕士，工程师，主要研究方向为雷达总体设计。